5.7 三角函数的应用 同步练习(Word版含解析)
文档属性
| 名称 | 5.7 三角函数的应用 同步练习(Word版含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 146.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-04 05:43:54 | ||
图片预览


文档简介
《第七节 三角函数的应用》同步练习
一、基础巩固
知识点1 三角函数模型在物理中的应用
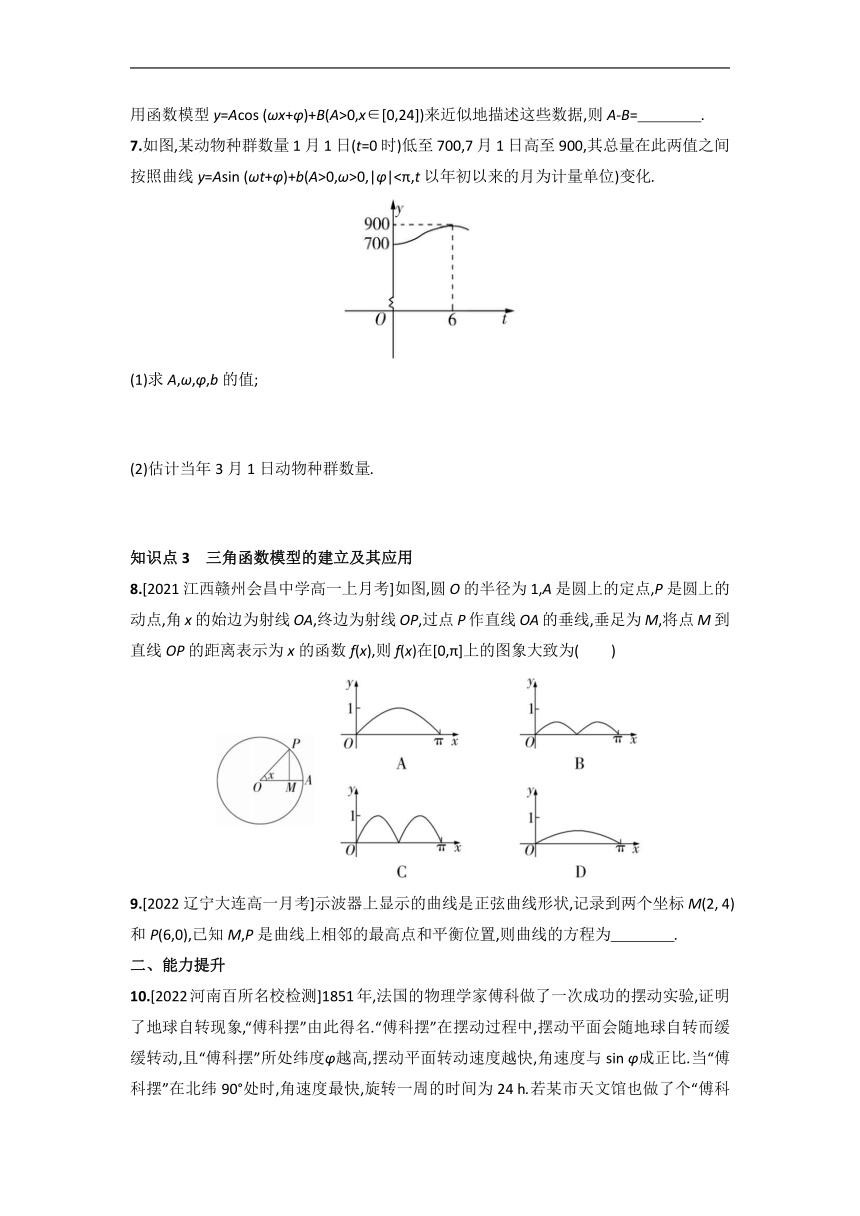
1.(多选)[2022广东广州执信中学高一下月考]如图所示的是一质点做简谐运动的图象,则( )
A.该质点的简谐运动周期为0.7 s
B.该质点的简谐运动振幅为5 cm
C.该质点的简谐运动频率为1.25 Hz
D.该质点的简谐运动周期为0.8 s
2.[2022广东深圳一模]阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置.深圳第一高楼平安金融中心的阻尼器减震装置是亚洲最大的阻尼器,被称为“镇楼神器”.由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其相对平衡位置的位移s(cm)和时间t(s)的函数关系式为s=2sin (ωt+φ),其中ω>0.若该阻尼器模型在摆动过程中连续三次相对平衡位置的位移为s0(-2A. B.π C. D.2π
3.[2022四川凉山宁南中学高一下开学考试]电流强度I(A)随时间t(s)变化的函数I=Asin (ωt+)(A>0,ω≠0)的图象如图所示,则当t= s时,电流强度是 .
4.如图,弹簧挂着的小球做上下振动,它在t(单位:s)时相对于平衡位置(静止时的位置)的高度h(单位:cm)由关系式h=Asin (ωt+)确定,其中A>0,ω>0,t∈[0,+∞).在一次振动中,小球从最高点运动至最低点所用时间为1 s,且最高点与最低点间的距离为10 cm.
(1)求小球相对平衡位置的高度h(单位:cm)和时间t(单位:s)之间的函数关系;
(2)若小球在t0 s内经过最高点的次数恰为50,求t0的取值范围.
知识点2 三角函数模型在生活中的应用
5.[2022江苏七市调研]时钟花原产于美洲热带,从开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20℃时,时钟酶活跃起来,花朵开始开放;当气温上升到28℃时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17 h的气温T(单位:℃)与时间t(单位:h)近似满足关系式T=20-10sin (t-),则该景区这天时钟花从开始开放到开始闭合约经历(参考数据:sin ≈0.8)( )
A.1.4 h B.2.4 h C.3.2 h D.5.6 h
6.[2022重庆巴蜀中学高一上期末]潮汐是发生在沿海地区的一种自然现象,是指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动.习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流.早先的人们为了表示生潮的时刻,把发生在早晨的高潮叫潮,发生在晚上的高潮叫汐,这是潮汐名称的由来.下表中给出了某市码头某一天水深与时间的关系(夜间零点开始计时).
时刻t 0 2 4 6 8 10 12
水深y/m 5.0 4.8 4.7 4.6 4.4 4.3 4.2
时刻t 14 16 18 20 22 24
水深y/m 4.3 4.4 4.6 4.7 4.8 5.0
用函数模型y=Acos (ωx+φ)+B(A>0,x∈[0,24])来近似地描述这些数据,则A-B= .
7.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间按照曲线y=Asin (ωt+φ)+b(A>0,ω>0,|φ|<π,t以年初以来的月为计量单位)变化.
(1)求A,ω,φ,b的值;
(2)估计当年3月1日动物种群数量.
知识点3 三角函数模型的建立及其应用
8.[2021江西赣州会昌中学高一上月考]如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则f(x)在[0,π]上的图象大致为( )
9.[2022辽宁大连高一月考]示波器上显示的曲线是正弦曲线形状,记录到两个坐标M(2, 4)和P(6,0),已知M,P是曲线上相邻的最高点和平衡位置,则曲线的方程为 .
二、能力提升
10.[2022河南百所名校检测]1851年,法国的物理学家傅科做了一次成功的摆动实验,证明了地球自转现象,“傅科摆”由此得名.“傅科摆”在摆动过程中,摆动平面会随地球自转而缓缓转动,且“傅科摆”所处纬度φ越高,摆动平面转动速度越快,角速度与sin φ成正比.当“傅科摆”在北纬90°处时,角速度最快,旋转一周的时间为24 h.若某市天文馆也做了个“傅科摆”,已知该天文馆处于北纬40°,那么此处“傅科摆”旋转一周的时间约为(参考数据:sin 40°≈0.64)( )
A.15.4 h B.24 h C.37.5 h D.54 h
11.[2022湖北省武昌实验中学高一期末]如图,摩天轮上一点P距离地面的高度y(m)与时间t(min)满足y=Asin (ωt+φ)+B,A>0,ω>0,φ∈[-π,π],已知某摩天轮的半径为50 m,点O距地面的高度为60 m,摩天轮做匀速运动,每10 min转一圈,点P的起始位置在摩天轮的最低点,则y关于t的解析式为( )
A.y=60-50sin t(t>0)
B.y=60-50cos t(t>0)
C.y=60-50cos t(t>0)
D.y=60-50sin t(t>0)
12.(多选)[2022福建漳州高一上期末]气候变化问题是人类面临的全球性问题,随着各国二氧化碳排放,温室气体猛增,对生命系统形成威胁.中国积极参与全球气候治理,加速全社会绿色低碳转型,力争2030年前实现碳达峰,2060年前实现碳中和目标.某校高一数学研究性学习小组同学研究的课题是“碳排放与气候变化问题”,研究小组观察记录某天从6 h到14 h的温度变化,其变化曲线近似满足函数f(x)=Asin (ωx+φ)+b(A>0,ω>0,0<φ<π),图象如图,则下列说法正确的是( )
A.φ=
B.函数f(x)的最小正周期为16π
C. x∈R,f(x)+f(x+8)=40
D.若g(x)=f(x+m)是偶函数,则|m|的最小值为2
13.某海滨浴场一天的海浪高度y(m)是时间t(0≤t≤24)(h)的函数,记作y=f(t),下表是某天各时的浪高数据:
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
(1)选用一个三角函数来近似描述这个海滨浴场的海浪高度y与时间t的函数关系;
(2)依据规定,当海浪高度不少于1 m时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的8 h至20 h之间,有多少时间可供冲浪爱好者进行冲浪
参考答案
一、基础巩固
1.BCD 由题图可知,运动周期为2×(0.7-0.3)=0.8(s),故A错,D正确;该简谐运动的振幅为5 cm,B正确;该简谐运动的频率f==1.25(Hz),得C正确.故选BCD.
2.B 不妨考虑如图所示的情况,则T=t3-t1=2,则=2,可得ω=π.
3.5 A 解:由题图可知,A=10,且该函数的最小正周期T=2×()=,则ω==100π,所以I=10sin(100πt+).当t= s时,I=10sin(100π×)=10sin (2π+)=10sin =5(A).
4. 解:(1)因为小球振动过程中最高点与最低点的距离为10 cm,所以A==5.
因为在一次振动中,小球从最高点运动至最低点所用时间为1 s,所以最小正周期为2,
即T=2=,所以ω=π,所以h=5sin(πt+),t≥0.
(2)由题意,当t= s时,小球第一次到达最高点,以后每隔一个最小正周期都到达一次最高点.
因为小球在t0 s内经过最高点的次数恰为50,
所以+49T≤t0<+50T.
因为T=2,所以98≤t0<100,
所以t0的取值范围为[98,100).
5.B 设t1 h开始开放,t2 h开始闭合,则20-10sin(t1-)=20,又t1∈[5,17],解得t1=9.又20-10sin(t2-)=28,所以sin(t2-)=-.由sin ≈0.8,得sin ≈-,结合题意,得t2-,所以t2=,所以t2-t1==2.4.故选B.
6.-4.2 解:从表中数据可知,函数的最大值为5.0,最小值为4.2,所以解得A=0.4,B=4.6,故A-B=-4.2.
7. 解:(1)由题图,得解得
又周期T=2×6=12,所以ω=,
所以y=100sin(t+φ)+800.
又当t=6时,y=900,
所以900=100sin(×6+φ)+800,所以sin(π+φ)=1,
所以sin φ=-1,又|φ|<π,所以φ=-.
(2)由(1)知y=100sin(t-)+800,
当t=2时,y=100sin(×2-)+800=750,
即当年3月1日动物种群数量约是750.
8.B
9.y=4sin(x+)
解:由题意可设曲线方程为y=4sin(ωx+φ)(ω>0).因为=4,所以T=16,所以ω=,所以y=4sin(x+φ).又曲线经过最高点M(2,4),所以×2+φ=+2kπ,k∈Z,所以φ=+2kπ,k∈Z,所以y=4sin(x+).
二、能力提升
10.C 设角速度ω=ksin φ(k≠0),故旋转一周所用的时间t=.当φ=90°=时,t=24,故k=,所以t=.故当“傅科摆”处于北纬40°时,t=≈37.5(h).
11.B 由题意得函数y=Asin(ωt+φ)+B的最大值为110,最小值为10,因此有解得A=50,B=60.又函数y=Asin(ωt+φ)+B的周期为10,即T=10,则ω=.又当t=0时,ymin=10,则sin φ=-1.又φ∈[-π,π],解得φ=-,所以y=50sin(t-)+60=60-50cos t(t>0).
12.ACD
13. 解:(1)以时间为横坐标,海浪高度为纵坐标,在平面直角坐标系中画出散点图,如图所示:
依据散点图,可以选用函数y=Asin(ωt+φ)+h(A>0,ω>0,|φ|≤)来近似描述这个海滨浴场的海浪高度y与时间t的函数关系.
从表中数据和散点图,可知A=,T=12,所以=12,得ω=.
又h==1,于是y=sin(t+φ)+1.
由图,知×0+φ=+2kπ,k∈Z,
又|φ|≤,所以φ=,
从而y=sin(t+)+1,即y= t+1(0≤t≤24).
(2)由题意,可知y≥1,
所以 t+1≥1,即cos t≥0,
所以2kπ-≤t≤2kπ+(k∈Z),
即12k-3≤t≤12k+3(k∈Z).
又0≤t≤24,所以0≤t≤3或9≤t≤15或21≤t≤24.
故一天内的8 h至20 h之间有6 h可供冲浪爱好者进行冲浪,即9 h至15 h.
一、基础巩固
知识点1 三角函数模型在物理中的应用
1.(多选)[2022广东广州执信中学高一下月考]如图所示的是一质点做简谐运动的图象,则( )
A.该质点的简谐运动周期为0.7 s
B.该质点的简谐运动振幅为5 cm
C.该质点的简谐运动频率为1.25 Hz
D.该质点的简谐运动周期为0.8 s
2.[2022广东深圳一模]阻尼器是一种以提供运动的阻力,从而达到减振效果的专业工程装置.深圳第一高楼平安金融中心的阻尼器减震装置是亚洲最大的阻尼器,被称为“镇楼神器”.由物理学知识可知,某阻尼器模型的运动过程可近似为单摆运动,其相对平衡位置的位移s(cm)和时间t(s)的函数关系式为s=2sin (ωt+φ),其中ω>0.若该阻尼器模型在摆动过程中连续三次相对平衡位置的位移为s0(-2
3.[2022四川凉山宁南中学高一下开学考试]电流强度I(A)随时间t(s)变化的函数I=Asin (ωt+)(A>0,ω≠0)的图象如图所示,则当t= s时,电流强度是 .
4.如图,弹簧挂着的小球做上下振动,它在t(单位:s)时相对于平衡位置(静止时的位置)的高度h(单位:cm)由关系式h=Asin (ωt+)确定,其中A>0,ω>0,t∈[0,+∞).在一次振动中,小球从最高点运动至最低点所用时间为1 s,且最高点与最低点间的距离为10 cm.
(1)求小球相对平衡位置的高度h(单位:cm)和时间t(单位:s)之间的函数关系;
(2)若小球在t0 s内经过最高点的次数恰为50,求t0的取值范围.
知识点2 三角函数模型在生活中的应用
5.[2022江苏七市调研]时钟花原产于美洲热带,从开放到闭合与体内的一种时钟酶有关.研究表明,当气温上升到20℃时,时钟酶活跃起来,花朵开始开放;当气温上升到28℃时,时钟酶的活性减弱,花朵开始闭合,且每天开闭一次.已知某景区一天内5~17 h的气温T(单位:℃)与时间t(单位:h)近似满足关系式T=20-10sin (t-),则该景区这天时钟花从开始开放到开始闭合约经历(参考数据:sin ≈0.8)( )
A.1.4 h B.2.4 h C.3.2 h D.5.6 h
6.[2022重庆巴蜀中学高一上期末]潮汐是发生在沿海地区的一种自然现象,是指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动.习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流.早先的人们为了表示生潮的时刻,把发生在早晨的高潮叫潮,发生在晚上的高潮叫汐,这是潮汐名称的由来.下表中给出了某市码头某一天水深与时间的关系(夜间零点开始计时).
时刻t 0 2 4 6 8 10 12
水深y/m 5.0 4.8 4.7 4.6 4.4 4.3 4.2
时刻t 14 16 18 20 22 24
水深y/m 4.3 4.4 4.6 4.7 4.8 5.0
用函数模型y=Acos (ωx+φ)+B(A>0,x∈[0,24])来近似地描述这些数据,则A-B= .
7.如图,某动物种群数量1月1日(t=0时)低至700,7月1日高至900,其总量在此两值之间按照曲线y=Asin (ωt+φ)+b(A>0,ω>0,|φ|<π,t以年初以来的月为计量单位)变化.
(1)求A,ω,φ,b的值;
(2)估计当年3月1日动物种群数量.
知识点3 三角函数模型的建立及其应用
8.[2021江西赣州会昌中学高一上月考]如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,过点P作直线OA的垂线,垂足为M,将点M到直线OP的距离表示为x的函数f(x),则f(x)在[0,π]上的图象大致为( )
9.[2022辽宁大连高一月考]示波器上显示的曲线是正弦曲线形状,记录到两个坐标M(2, 4)和P(6,0),已知M,P是曲线上相邻的最高点和平衡位置,则曲线的方程为 .
二、能力提升
10.[2022河南百所名校检测]1851年,法国的物理学家傅科做了一次成功的摆动实验,证明了地球自转现象,“傅科摆”由此得名.“傅科摆”在摆动过程中,摆动平面会随地球自转而缓缓转动,且“傅科摆”所处纬度φ越高,摆动平面转动速度越快,角速度与sin φ成正比.当“傅科摆”在北纬90°处时,角速度最快,旋转一周的时间为24 h.若某市天文馆也做了个“傅科摆”,已知该天文馆处于北纬40°,那么此处“傅科摆”旋转一周的时间约为(参考数据:sin 40°≈0.64)( )
A.15.4 h B.24 h C.37.5 h D.54 h
11.[2022湖北省武昌实验中学高一期末]如图,摩天轮上一点P距离地面的高度y(m)与时间t(min)满足y=Asin (ωt+φ)+B,A>0,ω>0,φ∈[-π,π],已知某摩天轮的半径为50 m,点O距地面的高度为60 m,摩天轮做匀速运动,每10 min转一圈,点P的起始位置在摩天轮的最低点,则y关于t的解析式为( )
A.y=60-50sin t(t>0)
B.y=60-50cos t(t>0)
C.y=60-50cos t(t>0)
D.y=60-50sin t(t>0)
12.(多选)[2022福建漳州高一上期末]气候变化问题是人类面临的全球性问题,随着各国二氧化碳排放,温室气体猛增,对生命系统形成威胁.中国积极参与全球气候治理,加速全社会绿色低碳转型,力争2030年前实现碳达峰,2060年前实现碳中和目标.某校高一数学研究性学习小组同学研究的课题是“碳排放与气候变化问题”,研究小组观察记录某天从6 h到14 h的温度变化,其变化曲线近似满足函数f(x)=Asin (ωx+φ)+b(A>0,ω>0,0<φ<π),图象如图,则下列说法正确的是( )
A.φ=
B.函数f(x)的最小正周期为16π
C. x∈R,f(x)+f(x+8)=40
D.若g(x)=f(x+m)是偶函数,则|m|的最小值为2
13.某海滨浴场一天的海浪高度y(m)是时间t(0≤t≤24)(h)的函数,记作y=f(t),下表是某天各时的浪高数据:
t 0 3 6 9 12 15 18 21 24
y 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
(1)选用一个三角函数来近似描述这个海滨浴场的海浪高度y与时间t的函数关系;
(2)依据规定,当海浪高度不少于1 m时才对冲浪爱好者开放海滨浴场,请依据(1)的结论,判断一天内的8 h至20 h之间,有多少时间可供冲浪爱好者进行冲浪
参考答案
一、基础巩固
1.BCD 由题图可知,运动周期为2×(0.7-0.3)=0.8(s),故A错,D正确;该简谐运动的振幅为5 cm,B正确;该简谐运动的频率f==1.25(Hz),得C正确.故选BCD.
2.B 不妨考虑如图所示的情况,则T=t3-t1=2,则=2,可得ω=π.
3.5 A 解:由题图可知,A=10,且该函数的最小正周期T=2×()=,则ω==100π,所以I=10sin(100πt+).当t= s时,I=10sin(100π×)=10sin (2π+)=10sin =5(A).
4. 解:(1)因为小球振动过程中最高点与最低点的距离为10 cm,所以A==5.
因为在一次振动中,小球从最高点运动至最低点所用时间为1 s,所以最小正周期为2,
即T=2=,所以ω=π,所以h=5sin(πt+),t≥0.
(2)由题意,当t= s时,小球第一次到达最高点,以后每隔一个最小正周期都到达一次最高点.
因为小球在t0 s内经过最高点的次数恰为50,
所以+49T≤t0<+50T.
因为T=2,所以98≤t0<100,
所以t0的取值范围为[98,100).
5.B 设t1 h开始开放,t2 h开始闭合,则20-10sin(t1-)=20,又t1∈[5,17],解得t1=9.又20-10sin(t2-)=28,所以sin(t2-)=-.由sin ≈0.8,得sin ≈-,结合题意,得t2-,所以t2=,所以t2-t1==2.4.故选B.
6.-4.2 解:从表中数据可知,函数的最大值为5.0,最小值为4.2,所以解得A=0.4,B=4.6,故A-B=-4.2.
7. 解:(1)由题图,得解得
又周期T=2×6=12,所以ω=,
所以y=100sin(t+φ)+800.
又当t=6时,y=900,
所以900=100sin(×6+φ)+800,所以sin(π+φ)=1,
所以sin φ=-1,又|φ|<π,所以φ=-.
(2)由(1)知y=100sin(t-)+800,
当t=2时,y=100sin(×2-)+800=750,
即当年3月1日动物种群数量约是750.
8.B
9.y=4sin(x+)
解:由题意可设曲线方程为y=4sin(ωx+φ)(ω>0).因为=4,所以T=16,所以ω=,所以y=4sin(x+φ).又曲线经过最高点M(2,4),所以×2+φ=+2kπ,k∈Z,所以φ=+2kπ,k∈Z,所以y=4sin(x+).
二、能力提升
10.C 设角速度ω=ksin φ(k≠0),故旋转一周所用的时间t=.当φ=90°=时,t=24,故k=,所以t=.故当“傅科摆”处于北纬40°时,t=≈37.5(h).
11.B 由题意得函数y=Asin(ωt+φ)+B的最大值为110,最小值为10,因此有解得A=50,B=60.又函数y=Asin(ωt+φ)+B的周期为10,即T=10,则ω=.又当t=0时,ymin=10,则sin φ=-1.又φ∈[-π,π],解得φ=-,所以y=50sin(t-)+60=60-50cos t(t>0).
12.ACD
13. 解:(1)以时间为横坐标,海浪高度为纵坐标,在平面直角坐标系中画出散点图,如图所示:
依据散点图,可以选用函数y=Asin(ωt+φ)+h(A>0,ω>0,|φ|≤)来近似描述这个海滨浴场的海浪高度y与时间t的函数关系.
从表中数据和散点图,可知A=,T=12,所以=12,得ω=.
又h==1,于是y=sin(t+φ)+1.
由图,知×0+φ=+2kπ,k∈Z,
又|φ|≤,所以φ=,
从而y=sin(t+)+1,即y= t+1(0≤t≤24).
(2)由题意,可知y≥1,
所以 t+1≥1,即cos t≥0,
所以2kπ-≤t≤2kπ+(k∈Z),
即12k-3≤t≤12k+3(k∈Z).
又0≤t≤24,所以0≤t≤3或9≤t≤15或21≤t≤24.
故一天内的8 h至20 h之间有6 h可供冲浪爱好者进行冲浪,即9 h至15 h.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
