人教版九年级上册22.3实际问题与二次函数(第二课时)课件(共16张PPT)
文档属性
| 名称 | 人教版九年级上册22.3实际问题与二次函数(第二课时)课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 733.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-04 09:42:08 | ||
图片预览






文档简介
(共16张PPT)
第二十二章 二次函数
22.3 实际问题与二次函数(第二课时)
拱桥问题
人教版 九年级上册
晓老师课堂
学习目标
1.了解实物抛物线
2.能够分析和表示实际问题中变量之间的二次函数关系,
正确建立坐标系.
3.并运用二次函数的图象、性质解决
2.列出二次函数的解析式,确定自变量的取值范围;
3.在自变量的取值范围内,求出二次函数的最大值或最小值.
1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当 时,二次函数 y = ax 2 + bx + c 有最
小(大)值
知识回顾
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
拱桥问题
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
拱桥问题
思考
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
拱桥问题
想解抛物线问题需要建立平面直角坐标系
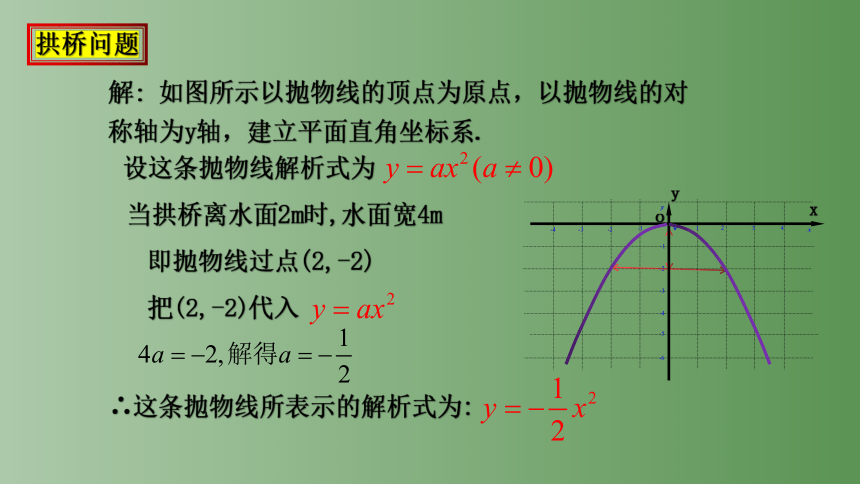
解: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
设这条抛物线解析式为
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的解析式为:
拱桥问题
把(2,-2)代入
x
y
0
-4
-3
-2
-1
1
2
3
4
-5
-3
-2
-1
-4
-6
x
y
o
拱桥问题
x
y
0
-4
-3
-2
-1
1
2
3
4
-5
-3
-2
-1
-4
-6
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
当水面下降1m时,水面的纵坐标为y=-3
x
y
o
解法二:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
设这条抛物线所表示的二次函数的解析式为:
(2,2)
-2
-1
拱桥问题
∵抛物线过点(0,0)
x
y
o
解法二:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
(2,2)
-2
-1
拱桥问题
x
y
o
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴这时水面的宽度为:
如图是一抛物线形的隧道,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过隧道,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过隧道 若能,请你通过计算加以说明;若不能,请简要说明理由.
跟踪练习
解:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.
∵AB=4
∴A(-2,0) B(2,0)
∵OC=4.4
∴C(0,4.4)
设抛物线所表示的二次函数为
跟踪练习
1.如图所示,市政府楼前喷水池喷出的抛物线形水柱,其解析式为 ,则水柱的最大高度是( ).
A.2 B.4 C.6 D.2+
C
当堂检测
2.已知二次函数 的图象如图所示,有下列5个结论:
①abc>0; ②b③4a+2b+c>0;
④2c<3b;
⑤ a+b>m(am+b)(m为不等于1的实数).
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
B
当堂检测
有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.
(1)如图求出这条抛物线表示的函数 的解析式;
(2)设正常水位时桥下的水深为 2 m,为保证过往船只顺利航行,桥下水面的宽度不得小于 18 m.求水深超过多少 m 时就会影响过往船只在桥下顺利航行.
O
A
C
D
B
y
x
20 m
h
当堂检测
坚持就是胜利
第二十二章 二次函数
22.3 实际问题与二次函数(第二课时)
拱桥问题
人教版 九年级上册
晓老师课堂
学习目标
1.了解实物抛物线
2.能够分析和表示实际问题中变量之间的二次函数关系,
正确建立坐标系.
3.并运用二次函数的图象、性质解决
2.列出二次函数的解析式,确定自变量的取值范围;
3.在自变量的取值范围内,求出二次函数的最大值或最小值.
1.由于抛物线 y = ax 2 + bx + c 的顶点是最低(高)点,当 时,二次函数 y = ax 2 + bx + c 有最
小(大)值
知识回顾
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
拱桥问题
(1)求宽度增加多少需要什么数据?
(2)表示水面宽的线段的端点在哪条曲线上?
(3)如何求这组数据?需要先求什么?
(4)图中还知道什么?
(5)怎样求抛物线对应的函数的解析式?
拱桥问题
思考
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
拱桥问题
想解抛物线问题需要建立平面直角坐标系
解: 如图所示以抛物线的顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系.
设这条抛物线解析式为
当拱桥离水面2m时,水面宽4m
即抛物线过点(2,-2)
∴这条抛物线所表示的解析式为:
拱桥问题
把(2,-2)代入
x
y
0
-4
-3
-2
-1
1
2
3
4
-5
-3
-2
-1
-4
-6
x
y
o
拱桥问题
x
y
0
-4
-3
-2
-1
1
2
3
4
-5
-3
-2
-1
-4
-6
图中是抛物线形拱桥,当拱顶离水面2m时,水面宽4m.水面下降1m,水面宽度增加多少?
当水面下降1m时,水面的纵坐标为y=-3
x
y
o
解法二:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
设这条抛物线所表示的二次函数的解析式为:
(2,2)
-2
-1
拱桥问题
∵抛物线过点(0,0)
x
y
o
解法二:如图所示,以抛物线和水面的两个交点的连线为x轴,以其中的一个交点(如左边的点)为原点,建立平面直角坐标系.
(2,2)
-2
-1
拱桥问题
x
y
o
当水面下降1m时,水面的纵坐标为y=-1,这时有:
∴这时水面的宽度为:
如图是一抛物线形的隧道,大门底部宽AB=4m,顶部C离地面的高度为4.4m,现有载满货物的汽车欲通过隧道,货物顶部距地面2.7m,装货宽度为2.4m.这辆汽车能否顺利通过隧道 若能,请你通过计算加以说明;若不能,请简要说明理由.
跟踪练习
解:如图,以AB所在的直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系.
∵AB=4
∴A(-2,0) B(2,0)
∵OC=4.4
∴C(0,4.4)
设抛物线所表示的二次函数为
跟踪练习
1.如图所示,市政府楼前喷水池喷出的抛物线形水柱,其解析式为 ,则水柱的最大高度是( ).
A.2 B.4 C.6 D.2+
C
当堂检测
2.已知二次函数 的图象如图所示,有下列5个结论:
①abc>0; ②b
④2c<3b;
⑤ a+b>m(am+b)(m为不等于1的实数).
其中正确的结论有( )
A.2个 B.3个 C.4个 D.5个
B
当堂检测
有一座抛物线形拱桥,正常水位时桥下水面宽度为 20 m,拱顶距离水面 4 m.
(1)如图求出这条抛物线表示的函数 的解析式;
(2)设正常水位时桥下的水深为 2 m,为保证过往船只顺利航行,桥下水面的宽度不得小于 18 m.求水深超过多少 m 时就会影响过往船只在桥下顺利航行.
O
A
C
D
B
y
x
20 m
h
当堂检测
坚持就是胜利
同课章节目录
