1.1.3 空间向量的坐标与空间直角坐标系 同步课时训练(Word版含解析)
文档属性
| 名称 | 1.1.3 空间向量的坐标与空间直角坐标系 同步课时训练(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 399.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-04 00:00:00 | ||
图片预览


文档简介
1.1.3 空间向量的坐标与空间直角坐标系
概念练习
1.已知点,,,则的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
2.已知向量,则等于( )
A. B.3 C. D.9
3.已知,,,若A,B,C,D四点共面,则实数( )
A.5 B.6 C.7 D.8
4.已知,,,则( )
A. B. C. D.
5.设点,,,若,则点B的坐标为( )
A. B. C. D.
二、能力提升
6.在空间直角坐标系中,已知点,,则线段的中点坐标是( )
A. B. C. D.
7.在空间直角坐标系中,记点在平面内射影的坐标为点B,则( )
A. B. C. D.
(多选)
8.设几何体是棱长为a的正方体,与相交于点O,则( )
A. B. C. D.
9.已知向量,,则下列结论中正确的是( )
A.若,则 B.若,则
C.不存在实数,使得 D.若,则
10.已知向量,,,下列等式中正确的是( )
A. B.
C. D.
11.若,,则与同方向的单位向量是_____________.
12.已知,则__________.
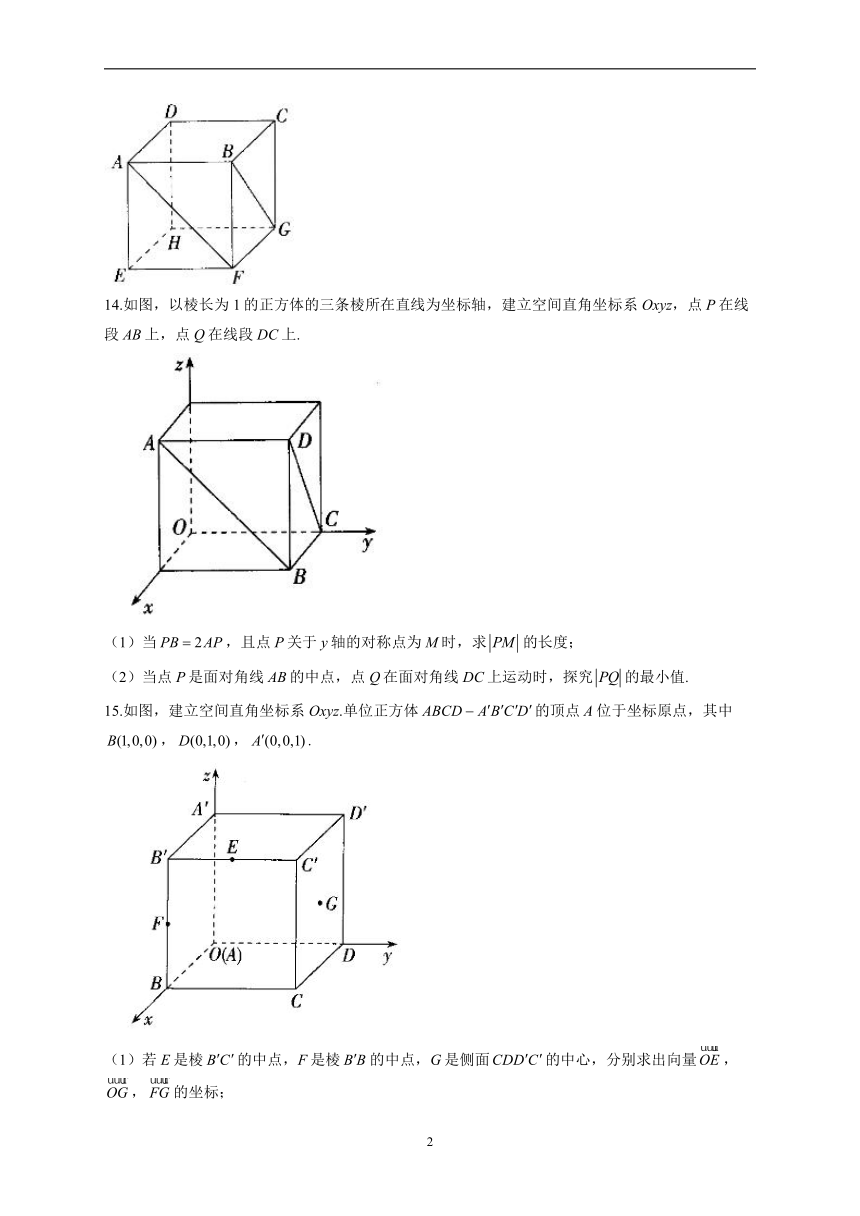
13.棱长为1的正方体如图所示,M,N分别为直线AF,BG上的动点,则线段MN长度的最小值为____________.
14.如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在线段AB上,点Q在线段DC上.
(1)当,且点P关于y轴的对称点为M时,求的长度;
(2)当点P是面对角线AB的中点,点Q在面对角线DC上运动时,探究的最小值.
15.如图,建立空间直角坐标系Oxyz.单位正方体的顶点A位于坐标原点,其中,,.
(1)若E是棱的中点,F是棱的中点,G是侧面的中心,分别求出向量,,的坐标;
(2)在(1)的条件下,分别求出,的值.
答案以及解析
1.答案:C
解析:,,,所以,,,所以.所以为直角三角形.故选C.
2.答案:C
解析:∵向量,
∴,
∴.
故选:C.
3.答案:D
解析:若A,B,C,D四点共面,则存在实数x,y使得成立,
则,解得.
4.答案:C
解析:.
5.答案:C
解析:设点B的坐标为,则,,,,解得,故选:C.
6.答案:B
解析:因为点,,所以线段AB的中点坐标是,即.故选:B.
7.答案:B
解析:求出B点坐标,然后计算.
点在xOz平面内的正投影为点,
则.故选:B.
8.答案:AC
解析:如图,建立空间直角坐标系,则,,,,,,,,,,,,,.,A对;,B错;,C对;,D错.故选AC.
9.答案:AC
解析:由得,
解得,故A选项正确;由
得,解得,故B选项错误;
若存在实数,使得,则,
,,显然无解,
即不存在实数使得,故C选项正确;
若,则,解得,
于是,故D选项错误.
10.答案:BCD
解析:易得.
,,所以A选项错误;
,所以,所以B选项正确;
,所以C选项正确;
,
即,,所以D选项正确.
故选BCD.
11.答案:
解析:与同方向的单位向量是.
12.答案:
解析:∵,
∴.
故答案为:.
13.答案:
解析:以H为原点,,,形成的方向分别为x轴,y轴,z轴正方向,建立如图所示的空间直角坐标系,则,,,,设,,则,,,当MN为两异面直线AF,BG的公垂线段时,MN的长度最短.
由得,
所以,,
所以.故答案为.
14.答案:(1)由题意知,,,.
由得,所以,所以.
(2)当点P是面对角线AB的中点时,,点Q在面对角线DC上运动,设点,,
则
,
所以当时,取得最小值,此时点.
15.答案:(1)由题图知,,,,,
,,,
.
(2),,.
2
概念练习
1.已知点,,,则的形状是( )
A.等腰三角形 B.等边三角形 C.直角三角形 D.等腰直角三角形
2.已知向量,则等于( )
A. B.3 C. D.9
3.已知,,,若A,B,C,D四点共面,则实数( )
A.5 B.6 C.7 D.8
4.已知,,,则( )
A. B. C. D.
5.设点,,,若,则点B的坐标为( )
A. B. C. D.
二、能力提升
6.在空间直角坐标系中,已知点,,则线段的中点坐标是( )
A. B. C. D.
7.在空间直角坐标系中,记点在平面内射影的坐标为点B,则( )
A. B. C. D.
(多选)
8.设几何体是棱长为a的正方体,与相交于点O,则( )
A. B. C. D.
9.已知向量,,则下列结论中正确的是( )
A.若,则 B.若,则
C.不存在实数,使得 D.若,则
10.已知向量,,,下列等式中正确的是( )
A. B.
C. D.
11.若,,则与同方向的单位向量是_____________.
12.已知,则__________.
13.棱长为1的正方体如图所示,M,N分别为直线AF,BG上的动点,则线段MN长度的最小值为____________.
14.如图,以棱长为1的正方体的三条棱所在直线为坐标轴,建立空间直角坐标系Oxyz,点P在线段AB上,点Q在线段DC上.
(1)当,且点P关于y轴的对称点为M时,求的长度;
(2)当点P是面对角线AB的中点,点Q在面对角线DC上运动时,探究的最小值.
15.如图,建立空间直角坐标系Oxyz.单位正方体的顶点A位于坐标原点,其中,,.
(1)若E是棱的中点,F是棱的中点,G是侧面的中心,分别求出向量,,的坐标;
(2)在(1)的条件下,分别求出,的值.
答案以及解析
1.答案:C
解析:,,,所以,,,所以.所以为直角三角形.故选C.
2.答案:C
解析:∵向量,
∴,
∴.
故选:C.
3.答案:D
解析:若A,B,C,D四点共面,则存在实数x,y使得成立,
则,解得.
4.答案:C
解析:.
5.答案:C
解析:设点B的坐标为,则,,,,解得,故选:C.
6.答案:B
解析:因为点,,所以线段AB的中点坐标是,即.故选:B.
7.答案:B
解析:求出B点坐标,然后计算.
点在xOz平面内的正投影为点,
则.故选:B.
8.答案:AC
解析:如图,建立空间直角坐标系,则,,,,,,,,,,,,,.,A对;,B错;,C对;,D错.故选AC.
9.答案:AC
解析:由得,
解得,故A选项正确;由
得,解得,故B选项错误;
若存在实数,使得,则,
,,显然无解,
即不存在实数使得,故C选项正确;
若,则,解得,
于是,故D选项错误.
10.答案:BCD
解析:易得.
,,所以A选项错误;
,所以,所以B选项正确;
,所以C选项正确;
,
即,,所以D选项正确.
故选BCD.
11.答案:
解析:与同方向的单位向量是.
12.答案:
解析:∵,
∴.
故答案为:.
13.答案:
解析:以H为原点,,,形成的方向分别为x轴,y轴,z轴正方向,建立如图所示的空间直角坐标系,则,,,,设,,则,,,当MN为两异面直线AF,BG的公垂线段时,MN的长度最短.
由得,
所以,,
所以.故答案为.
14.答案:(1)由题意知,,,.
由得,所以,所以.
(2)当点P是面对角线AB的中点时,,点Q在面对角线DC上运动,设点,,
则
,
所以当时,取得最小值,此时点.
15.答案:(1)由题图知,,,,,
,,,
.
(2),,.
2
