2022-2023学年人教版数学七年级上册3.4 实际问题与一元一次方程-配套问题 课件 (共20张PPT)
文档属性
| 名称 | 2022-2023学年人教版数学七年级上册3.4 实际问题与一元一次方程-配套问题 课件 (共20张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1014.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 09:02:20 | ||
图片预览






文档简介
(共20张PPT)
1
人教版数学七年级上册第三章第四节
3.4 实际问题与一元一次方程
配套问题
2
什么叫配套
桌面与桌腿数量比为1:4
茶壶与茶杯数量比为1:3
螺钉与螺母数量比为1:2
问题引入,探究起始
配套比
列方程
3
理解配套
问题引入,探究起始
配套比1:2
若一块鸡肉和两块面包可以配成一个汉堡包,
则要用_____块鸡肉才能和10块面包刚好配套,
若现有a块鸡肉,则应需________块面包才能刚好配套。
5
2a
面包的数量是鸡肉数量的2倍
4
例题
深入探究,突破难点
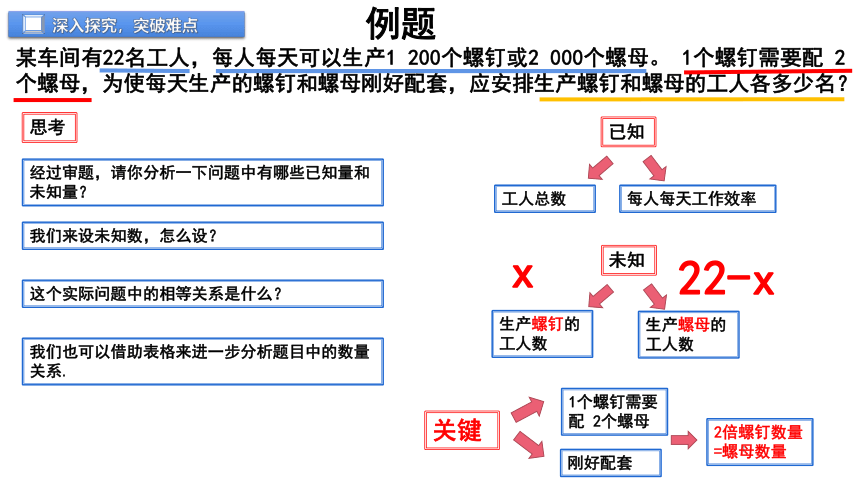
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
思考
经过审题,请你分析一下问题中有哪些已知量和未知量?
这个实际问题中的相等关系是什么?
我们来设未知数,怎么设?
我们也可以借助表格来进一步分析题目中的数量关系.
工人总数
每人每天工作效率
已知
未知
生产螺钉的工人数
生产螺母的工人数
关键
1个螺钉需要
配 2个螺母
刚好配套
2倍螺钉数量=螺母数量
x
22-x
例题
深入探究,突破难点
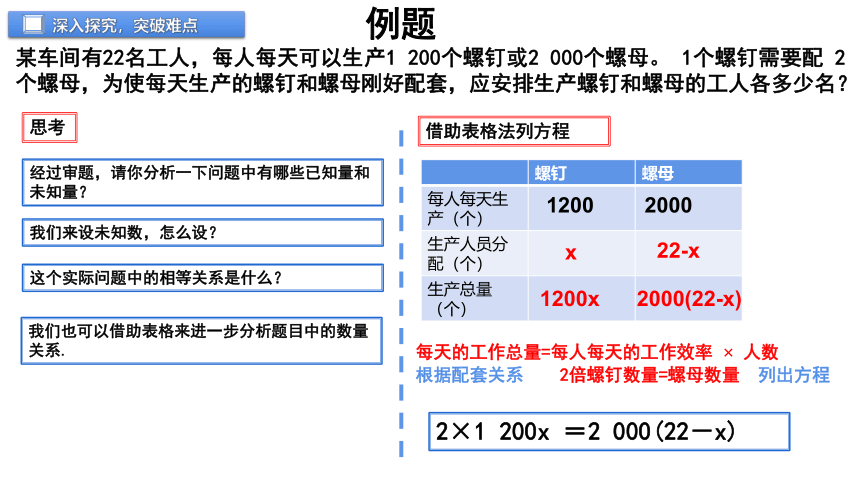
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
思考
经过审题,请你分析一下问题中有哪些已知量和未知量?
这个实际问题中的相等关系是什么?
我们来设未知数,怎么设?
我们也可以借助表格来进一步分析题目中的数量关系.
螺钉 螺母
每人每天生产(个)
生产人员分配(个)
生产总量(个)
借助表格法列方程
1200
2000
x
22-x
每天的工作总量=每人每天的工作效率 人数
1200x
2000(22-x)
根据配套关系 2倍螺钉数量=螺母数量 列出方程
2×1 200x =2 000(22-x)
例题
深入探究,突破难点
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
归纳总结:用方程解决实际问题的步骤
1.审题(寻找等量关系)
2.设(未知数)
3.列(依据等量关系列方程)
4.解(方程)
5.答(完整,呼应前面的未知数)
解题过程如下:
解:设应安排x名工人生产螺钉,
(22-x)名工人生产螺母.
依题意得:
2×1 200x =2 000(22-x)
解方程得:
5(22-x)=6x
110-5x=6x
x=10.
22-x=12
答:应安排10名工人生产螺钉,
12名工人生产螺母.
解决配套问题的方法
(1)抓住配套关系
(2)设出未知数
(3)根据配套关系
列出方程
(4)通过解方程
解决问题
变式演练,掌握新知
某车间有27名工人,生产甲、乙两种零件,每3个甲零件与2个乙零件配成一套,已知每个工人每天能加工甲零件12个或乙零件16个,为使每天生产的两种零件配套,应如何分配工人的生产任务?
配套关系
甲:乙=3:2
解:设应安排x名工人生产甲种零件,(27-x)名工人生产乙种零件.
依题意得:
3× 16× (27-x)=2×12x
即24x=48(27-x)
解方程得x=18
27-18=9
答:应安排18人生产甲种零件,9人生产乙种零件
甲种零件 乙种零件
每人每天生产(个)
生产人员分配(个)
生产总量(个)
12
16
x
27-x
12x
16× (27-x)
解题过程如下:
等量关系
3乙总=2甲总
(1)抓住配套关系
(2)设出未知数
(3)根据配套关系
列出方程
(4)通过解方程
解决问题
深化拓展,体悟新知
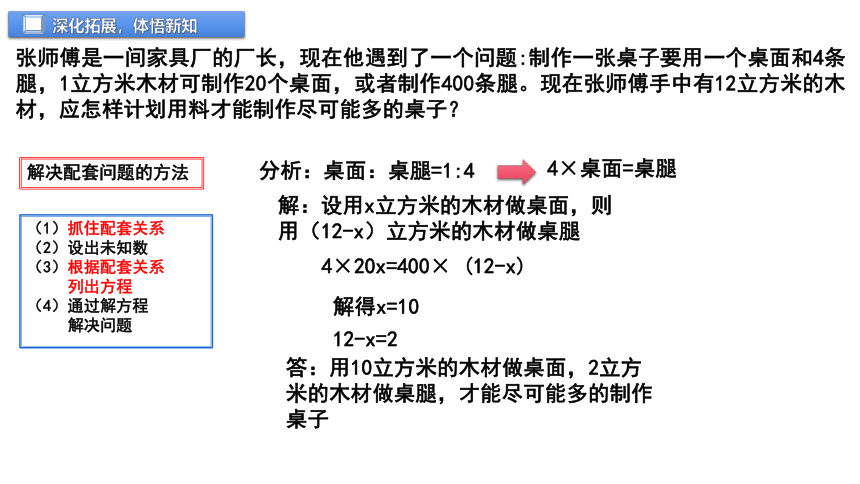
张师傅是一间家具厂的厂长,现在他遇到了一个问题:制作一张桌子要用一个桌面和4条腿,1立方米木材可制作20个桌面,或者制作400条腿。现在张师傅手中有12立方米的木材,应怎样计划用料才能制作尽可能多的桌子?
解决配套问题的方法
(1)抓住配套关系
(2)设出未知数
(3)根据配套关系
列出方程
(4)通过解方程
解决问题
分析:桌面:桌腿=1:4
4×桌面=桌腿
解:设用x立方米的木材做桌面,则用(12-x)立方米的木材做桌腿
4×20x=400× (12-x)
解得x=10
12-x=2
答:用10立方米的木材做桌面,2立方米的木材做桌腿,才能尽可能多的制作桌子
【课堂小结】
列一元一次方程解决实际问题
等量关系
式子
配套问题
理解其中的比例关系
关键
列方程解决实际问题
审、设、列、解、答
步骤
小结新课,梳理新知
10
3.4 实际问题与一元一次方程
销售中的盈亏
导入
一件衣服的进价是200元,卖了260元,这件衣服的利润是多少?
一件衣服的进价是260元,卖了220元,这件衣服的利润是多少?
利润为260-200=60
利润=220-260=-40
即售价-进价=利润
即售价-进价=-利润
导入
那么利润率呢?等于什么?
售价探究(温馨提示:规范操作、注意安全)
知识讲解
1. 某琴行卖出一架钢琴,售价为960元. 盈利20%,请问进价为多少?
盈利时:售价-进价=利润率×进价
解:设钢琴的进价为x元,根据题意得:
960-x= 20%x
X=800
答:钢琴的进价为800元。
售价探究(温馨提示:规范操作、注意安全)
知识讲解
2. 某琴行卖出一架钢琴,售价为960元,亏损20%,请问售价为多少?
亏损时:售价-进价=-利润率×进价
解:设钢琴的进价为x元,根据题意得:
960-x=- 20%x
X=1200
答:钢琴的进价为1200元。
A. 盈利
B. 亏损
C. 不盈不亏
问题1:你估计盈亏情况是怎样的?
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
思考:
销售的盈亏取决于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系
总售价(120元) > 总成本 盈 利
总售价(120元)< 总成本 亏 损
总售价(120元) = 总成本 不盈不亏
现在两件衣服的售价为已知条件,要知道卖这两件衣服是盈利还是
亏损,还需要知道什么?
两件衣服的成本(即进价).
如果设盈利的那件衣服的进价为x 元,根据进价、利润率、售价之间 的关系,你能列出方程求解吗?同理,如果设另一件衣服的进价为 y 元呢?
思考:
销售的盈亏取决于什么?
解:
(1) 设盈利25%的衣服进价是 x 元,
依题意得 x+0.25 x=60 解得 x=48.
(2) 设亏损25%的衣服进价是 y元,
依题意得 y-0.25y=60 解得 y=80.
两件衣服总成本:x+y=48+80=128 (元).
因为120-128=-8(元)
所以卖这两件衣服共亏损了8元.
课堂练习
18
某文具店有两个进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%.这次交易中的盈亏情况?
答案:这次交易盈利8元.
【课堂小结】
小结
销
售
中
的
盈
亏
●售价、进价、利润的关系:
商品利润
= 商品售价-商品进价
商品利润
利润率=
●进价、利润、利润率的关系:
商品进价
×100%
利润=售价-进价=利润率×成本
-利润=售价-进价=利润率×成本
20
同学们再见
1
人教版数学七年级上册第三章第四节
3.4 实际问题与一元一次方程
配套问题
2
什么叫配套
桌面与桌腿数量比为1:4
茶壶与茶杯数量比为1:3
螺钉与螺母数量比为1:2
问题引入,探究起始
配套比
列方程
3
理解配套
问题引入,探究起始
配套比1:2
若一块鸡肉和两块面包可以配成一个汉堡包,
则要用_____块鸡肉才能和10块面包刚好配套,
若现有a块鸡肉,则应需________块面包才能刚好配套。
5
2a
面包的数量是鸡肉数量的2倍
4
例题
深入探究,突破难点
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
思考
经过审题,请你分析一下问题中有哪些已知量和未知量?
这个实际问题中的相等关系是什么?
我们来设未知数,怎么设?
我们也可以借助表格来进一步分析题目中的数量关系.
工人总数
每人每天工作效率
已知
未知
生产螺钉的工人数
生产螺母的工人数
关键
1个螺钉需要
配 2个螺母
刚好配套
2倍螺钉数量=螺母数量
x
22-x
例题
深入探究,突破难点
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
思考
经过审题,请你分析一下问题中有哪些已知量和未知量?
这个实际问题中的相等关系是什么?
我们来设未知数,怎么设?
我们也可以借助表格来进一步分析题目中的数量关系.
螺钉 螺母
每人每天生产(个)
生产人员分配(个)
生产总量(个)
借助表格法列方程
1200
2000
x
22-x
每天的工作总量=每人每天的工作效率 人数
1200x
2000(22-x)
根据配套关系 2倍螺钉数量=螺母数量 列出方程
2×1 200x =2 000(22-x)
例题
深入探究,突破难点
某车间有22名工人,每人每天可以生产1 200个螺钉或2 000个螺母。 1个螺钉需要配 2个螺母,为使每天生产的螺钉和螺母刚好配套,应安排生产螺钉和螺母的工人各多少名?
归纳总结:用方程解决实际问题的步骤
1.审题(寻找等量关系)
2.设(未知数)
3.列(依据等量关系列方程)
4.解(方程)
5.答(完整,呼应前面的未知数)
解题过程如下:
解:设应安排x名工人生产螺钉,
(22-x)名工人生产螺母.
依题意得:
2×1 200x =2 000(22-x)
解方程得:
5(22-x)=6x
110-5x=6x
x=10.
22-x=12
答:应安排10名工人生产螺钉,
12名工人生产螺母.
解决配套问题的方法
(1)抓住配套关系
(2)设出未知数
(3)根据配套关系
列出方程
(4)通过解方程
解决问题
变式演练,掌握新知
某车间有27名工人,生产甲、乙两种零件,每3个甲零件与2个乙零件配成一套,已知每个工人每天能加工甲零件12个或乙零件16个,为使每天生产的两种零件配套,应如何分配工人的生产任务?
配套关系
甲:乙=3:2
解:设应安排x名工人生产甲种零件,(27-x)名工人生产乙种零件.
依题意得:
3× 16× (27-x)=2×12x
即24x=48(27-x)
解方程得x=18
27-18=9
答:应安排18人生产甲种零件,9人生产乙种零件
甲种零件 乙种零件
每人每天生产(个)
生产人员分配(个)
生产总量(个)
12
16
x
27-x
12x
16× (27-x)
解题过程如下:
等量关系
3乙总=2甲总
(1)抓住配套关系
(2)设出未知数
(3)根据配套关系
列出方程
(4)通过解方程
解决问题
深化拓展,体悟新知
张师傅是一间家具厂的厂长,现在他遇到了一个问题:制作一张桌子要用一个桌面和4条腿,1立方米木材可制作20个桌面,或者制作400条腿。现在张师傅手中有12立方米的木材,应怎样计划用料才能制作尽可能多的桌子?
解决配套问题的方法
(1)抓住配套关系
(2)设出未知数
(3)根据配套关系
列出方程
(4)通过解方程
解决问题
分析:桌面:桌腿=1:4
4×桌面=桌腿
解:设用x立方米的木材做桌面,则用(12-x)立方米的木材做桌腿
4×20x=400× (12-x)
解得x=10
12-x=2
答:用10立方米的木材做桌面,2立方米的木材做桌腿,才能尽可能多的制作桌子
【课堂小结】
列一元一次方程解决实际问题
等量关系
式子
配套问题
理解其中的比例关系
关键
列方程解决实际问题
审、设、列、解、答
步骤
小结新课,梳理新知
10
3.4 实际问题与一元一次方程
销售中的盈亏
导入
一件衣服的进价是200元,卖了260元,这件衣服的利润是多少?
一件衣服的进价是260元,卖了220元,这件衣服的利润是多少?
利润为260-200=60
利润=220-260=-40
即售价-进价=利润
即售价-进价=-利润
导入
那么利润率呢?等于什么?
售价探究(温馨提示:规范操作、注意安全)
知识讲解
1. 某琴行卖出一架钢琴,售价为960元. 盈利20%,请问进价为多少?
盈利时:售价-进价=利润率×进价
解:设钢琴的进价为x元,根据题意得:
960-x= 20%x
X=800
答:钢琴的进价为800元。
售价探究(温馨提示:规范操作、注意安全)
知识讲解
2. 某琴行卖出一架钢琴,售价为960元,亏损20%,请问售价为多少?
亏损时:售价-进价=-利润率×进价
解:设钢琴的进价为x元,根据题意得:
960-x=- 20%x
X=1200
答:钢琴的进价为1200元。
A. 盈利
B. 亏损
C. 不盈不亏
问题1:你估计盈亏情况是怎样的?
一商店在某一时间以每件60元的价格卖出两件衣服,其中一件盈利25% ,另一件亏损25% ,卖这两件衣服总的是盈利还是亏损,或是不盈不亏
思考:
销售的盈亏取决于什么?
取决于总售价与总成本(两件衣服的成本之和)的关系
总售价(120元) > 总成本 盈 利
总售价(120元)< 总成本 亏 损
总售价(120元) = 总成本 不盈不亏
现在两件衣服的售价为已知条件,要知道卖这两件衣服是盈利还是
亏损,还需要知道什么?
两件衣服的成本(即进价).
如果设盈利的那件衣服的进价为x 元,根据进价、利润率、售价之间 的关系,你能列出方程求解吗?同理,如果设另一件衣服的进价为 y 元呢?
思考:
销售的盈亏取决于什么?
解:
(1) 设盈利25%的衣服进价是 x 元,
依题意得 x+0.25 x=60 解得 x=48.
(2) 设亏损25%的衣服进价是 y元,
依题意得 y-0.25y=60 解得 y=80.
两件衣服总成本:x+y=48+80=128 (元).
因为120-128=-8(元)
所以卖这两件衣服共亏损了8元.
课堂练习
18
某文具店有两个进价不同的计算器都卖64元,其中一个盈利60%,另一个亏本20%.这次交易中的盈亏情况?
答案:这次交易盈利8元.
【课堂小结】
小结
销
售
中
的
盈
亏
●售价、进价、利润的关系:
商品利润
= 商品售价-商品进价
商品利润
利润率=
●进价、利润、利润率的关系:
商品进价
×100%
利润=售价-进价=利润率×成本
-利润=售价-进价=利润率×成本
20
同学们再见
