人教版七年级下册5.1相交线、垂线课件(共27张PPT)
文档属性
| 名称 | 人教版七年级下册5.1相交线、垂线课件(共27张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-04 00:00:00 | ||
图片预览








文档简介
(共27张PPT)
相交线、垂线知识讲解
【学习目标】
1.了解两直线相交所成的角的位置和大小关系,理解邻补角和对顶角概念,掌握对顶角的性质;
2.理解垂直作为两条直线相交的特殊情形,掌握垂直的定义及性质;
3.理解点到直线的距离的概念,并会度量点到直线的距离;
4.能依据对顶角、邻补角及垂直的概念与性质,进行简单的计算。
【要点梳理】
知识点一、邻补角与对顶角
1.邻补角:如果两个角有一条公共边,并且它们的另一边互为反向延长线,那么具有这种关系的两个角叫做互为邻补角。
【要点梳理】
知识点一、邻补角与对顶角
要点诠释:
(1)邻补角的定义既包含了位置关系,又包含了数量关系:“邻”指的是位置相邻,“补”指的是两个角的和为180°。
(2)邻补角是成对出现的,而且是“互为”邻补角。
(3)互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角。
(4)邻补角满足的条件:①有公共顶点;②有一条公共边,另一边互为反向延长线。
【要点梳理】
知识点一、邻补角与对顶角
2. 对顶角及性质:
(1)定义:由两条直线相交构成的四个角中,有公共顶点没有公共边(相对)的两个角,互为对顶角。
(2)性质:对顶角相等。
【要点梳理】
知识点一、邻补角与对顶角
要点诠释:
(1)由定义可知只有两条直线相交时,才能产生对顶角。
(2)对顶角满足的条件:①相等的两个角;②有公共顶点且一角的两边是另一角两边的反向延长线。
【要点梳理】
知识点一、邻补角与对顶角
3. 邻补角与对顶角对比:
角的名称 特 征 性 质 相 同 点 不 同 点
对顶角 ①两条直线相交形成的角; ②有一个公共顶点; ③没有公共边。 对顶角相等 ①都是两条直线相交而成的角; ②都有一个公共顶点; ③都是成对出现的。 ①有无公共边;
②两直线相交时,对顶角只有2对;邻补角有4对。
邻补角 ①两条直线相交而成; ②有一个公共顶点; ③有一条公共边。 邻补角互补
【要点梳理】
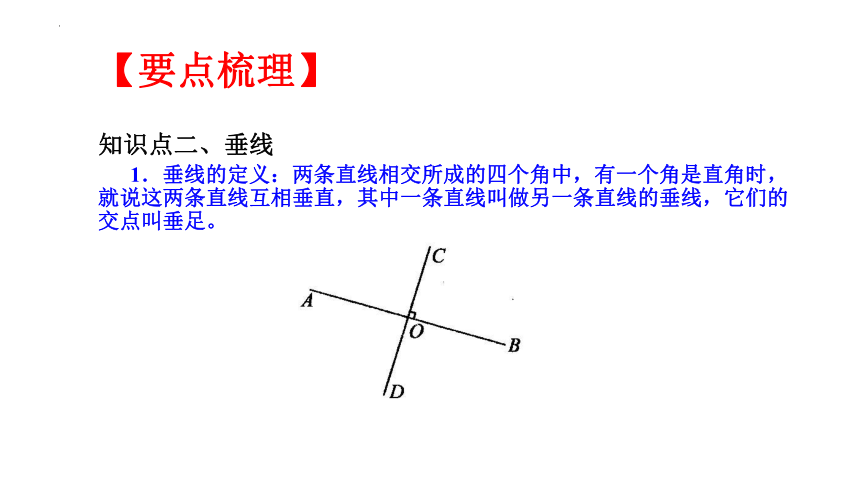
知识点二、垂线
1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足。
【要点梳理】
知识点二、垂线
要点诠释:
(1)记法:直线a与b垂直,记作:
直线AB和CD垂直于点O,记作:AB⊥CD于点O。
(2) 垂直的定义具有二重性,既可以作垂直的判定,又可以作垂直的性质,即有:
CD⊥AB。
【要点梳理】
知识点二、垂线
2.垂线的画法:过一点画已知直线的垂线,可通过直角三角板来画,具体方法是使直角三角板的一条直角边和已知直线重合,沿直线左右移动三角板,使另一条直角边经过已知点,沿此直角边画直线,则所画直线就为已知直线的垂线(如图所示)。
【要点梳理】
知识点二、垂线
要点诠释:
(1)如果过一点画已知射线或线段的垂线时,指的是它所在直线的垂线,垂足可能在射线的反向延长线上,也可能在线段的延长线上。
(2)过直线外一点作已知直线的垂线,这点与垂足间的线段为垂线段。
【要点梳理】
知识点二、垂线
3.垂线的性质:
(1)在同一平面内,过一点有且只有一条直线与已知直线垂直。
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。简单说成:垂线段最短。
【要点梳理】
知识点二、垂线
要点诠释:
(1)性质(1)成立的前提是在“同一平面内”,“有”表示存在,“只有”表示唯一,“有且只有”说明了垂线的存在性和唯一性。
(2)性质(2)是“连接直线外一点和直线上各点的所有线段中,垂线段最短。”实际上,连接直线外一点和直线上各点的线段有无数条,但只有一条最短,即垂线段最短。在实际问题中经常应用其“最短性”解决问题。
【要点梳理】
知识点二、垂线
4.点到直线的距离:
定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
【要点梳理】
知识点二、垂线
要点诠释:
(1)点到直线的距离是垂线段的长度,是一个数量,不能说垂线段是距离;
(2)求点到直线的距离时,要从已知条件中找出垂线段或画出垂线段,然后计算或度量垂线段的长度。
【典型例题】
1.如图所示,M、N是直线AB上两点,∠1=∠2,问∠1与∠2,∠3与∠4是对顶角吗 ∠1与∠5,∠3与∠6是邻补角吗?
【典型例题】
【答案与解析】
解:∠1和∠2,∠3和∠4都不是对顶角.∠1与∠5,∠3与∠6也都不是邻补角。
【总结升华】牢记两条直线相交,才能产生对顶角或邻补角。
【典型例题】
2.如图所示,直线AB、CD相交于点O,∠1=65°,求∠2、∠3、∠4的度数
【典型例题】
【答案与解析】
解:∵ ∠1是∠2的邻补角,∠1=65°,
∴ ∠2=180°-65°=115°
又∵ ∠1和∠3是对顶角,∠2与∠4是对顶角
∴ ∠3=∠1=65°, ∠4=∠2=115°
【总结升华】 (1)两条直线相交所成的四个角中,只要已知其中一个角,就可以求出另外三角;(2)求出∠2后用 “对顶角相等”,求∠3和∠4
【典型例题】
3. 任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角 各对角存在怎样的位置关系?根据这种位置关系将它们分类。
【典型例题】
【答案与解析】
解:如图,
任意两条相交直线,两两相配共组成6对角,在这6对角中,它们的位置关系有两种:①有公共顶点,一边重合,另一边互为反向延长线;②有公共顶点,角的两边互为反向延长线。
这6对角为∠1与∠2,∠1与∠3,∠1与∠4,∠2与∠3,∠2与∠4,∠3与∠4,其中∠1=∠3,∠2=∠4,∠1+∠2=180°,∠3+∠4=180°,∠1+∠4=180°,∠2+∠3=180°.在位置上∠1与∠3,∠2与∠4是对顶角,∠1与∠2,∠3与∠4,∠l与∠4,∠2与∠3是邻补角。
【总结升华】两条相交的直线,两两相配共组成6对角,这6对角中有:4对邻补角,2对对顶角。
【典型例题】
4.下列语句中,正确的有 ( )
①一条直线的垂线只有一条;
②在同一平面内,过直线上一点有且仅有一条直线与已知直线垂直;
③两直线相交,则交点叫垂足;
④互相垂直的两条直线形成的四个角一定都是直角。
A.0个 B.1个 C.2个 D.3个
【典型例题】
【答案】C
【解析】正确的是:②④
【总结升华】充分理解垂直的定义与性质。
【典型例题】
5.(河北模拟)如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
【典型例题】
【答案】C
【解析】解:∵∠1=145°,
∴∠2=180°﹣145°=35°,
∵CO⊥DO,
∴∠COD=90°,
∴∠3=90°﹣∠2=90°﹣35°=55°
【总结升华】本题考查了垂线和邻补角的定义;弄清两个角之间的互补和互余关系是解题的关键。
【典型例题】
6.(抚州校级期中)如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
【典型例题】
【思路点拨】根据垂线段最短可得答案。
【答案】A
【解析】解:根据垂线段最短可得:应建在A处,故选:A
【总结升华】此题主要考查了垂线段的性质,关键是掌握从直线外一点到这条直线所作的垂线段最短。
相交线、垂线知识讲解
【学习目标】
1.了解两直线相交所成的角的位置和大小关系,理解邻补角和对顶角概念,掌握对顶角的性质;
2.理解垂直作为两条直线相交的特殊情形,掌握垂直的定义及性质;
3.理解点到直线的距离的概念,并会度量点到直线的距离;
4.能依据对顶角、邻补角及垂直的概念与性质,进行简单的计算。
【要点梳理】
知识点一、邻补角与对顶角
1.邻补角:如果两个角有一条公共边,并且它们的另一边互为反向延长线,那么具有这种关系的两个角叫做互为邻补角。
【要点梳理】
知识点一、邻补角与对顶角
要点诠释:
(1)邻补角的定义既包含了位置关系,又包含了数量关系:“邻”指的是位置相邻,“补”指的是两个角的和为180°。
(2)邻补角是成对出现的,而且是“互为”邻补角。
(3)互为邻补角的两个角一定互补,但互补的两个角不一定互为邻补角。
(4)邻补角满足的条件:①有公共顶点;②有一条公共边,另一边互为反向延长线。
【要点梳理】
知识点一、邻补角与对顶角
2. 对顶角及性质:
(1)定义:由两条直线相交构成的四个角中,有公共顶点没有公共边(相对)的两个角,互为对顶角。
(2)性质:对顶角相等。
【要点梳理】
知识点一、邻补角与对顶角
要点诠释:
(1)由定义可知只有两条直线相交时,才能产生对顶角。
(2)对顶角满足的条件:①相等的两个角;②有公共顶点且一角的两边是另一角两边的反向延长线。
【要点梳理】
知识点一、邻补角与对顶角
3. 邻补角与对顶角对比:
角的名称 特 征 性 质 相 同 点 不 同 点
对顶角 ①两条直线相交形成的角; ②有一个公共顶点; ③没有公共边。 对顶角相等 ①都是两条直线相交而成的角; ②都有一个公共顶点; ③都是成对出现的。 ①有无公共边;
②两直线相交时,对顶角只有2对;邻补角有4对。
邻补角 ①两条直线相交而成; ②有一个公共顶点; ③有一条公共边。 邻补角互补
【要点梳理】
知识点二、垂线
1.垂线的定义:两条直线相交所成的四个角中,有一个角是直角时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫垂足。
【要点梳理】
知识点二、垂线
要点诠释:
(1)记法:直线a与b垂直,记作:
直线AB和CD垂直于点O,记作:AB⊥CD于点O。
(2) 垂直的定义具有二重性,既可以作垂直的判定,又可以作垂直的性质,即有:
CD⊥AB。
【要点梳理】
知识点二、垂线
2.垂线的画法:过一点画已知直线的垂线,可通过直角三角板来画,具体方法是使直角三角板的一条直角边和已知直线重合,沿直线左右移动三角板,使另一条直角边经过已知点,沿此直角边画直线,则所画直线就为已知直线的垂线(如图所示)。
【要点梳理】
知识点二、垂线
要点诠释:
(1)如果过一点画已知射线或线段的垂线时,指的是它所在直线的垂线,垂足可能在射线的反向延长线上,也可能在线段的延长线上。
(2)过直线外一点作已知直线的垂线,这点与垂足间的线段为垂线段。
【要点梳理】
知识点二、垂线
3.垂线的性质:
(1)在同一平面内,过一点有且只有一条直线与已知直线垂直。
(2)连接直线外一点与直线上各点的所有线段中,垂线段最短。简单说成:垂线段最短。
【要点梳理】
知识点二、垂线
要点诠释:
(1)性质(1)成立的前提是在“同一平面内”,“有”表示存在,“只有”表示唯一,“有且只有”说明了垂线的存在性和唯一性。
(2)性质(2)是“连接直线外一点和直线上各点的所有线段中,垂线段最短。”实际上,连接直线外一点和直线上各点的线段有无数条,但只有一条最短,即垂线段最短。在实际问题中经常应用其“最短性”解决问题。
【要点梳理】
知识点二、垂线
4.点到直线的距离:
定义:直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
【要点梳理】
知识点二、垂线
要点诠释:
(1)点到直线的距离是垂线段的长度,是一个数量,不能说垂线段是距离;
(2)求点到直线的距离时,要从已知条件中找出垂线段或画出垂线段,然后计算或度量垂线段的长度。
【典型例题】
1.如图所示,M、N是直线AB上两点,∠1=∠2,问∠1与∠2,∠3与∠4是对顶角吗 ∠1与∠5,∠3与∠6是邻补角吗?
【典型例题】
【答案与解析】
解:∠1和∠2,∠3和∠4都不是对顶角.∠1与∠5,∠3与∠6也都不是邻补角。
【总结升华】牢记两条直线相交,才能产生对顶角或邻补角。
【典型例题】
2.如图所示,直线AB、CD相交于点O,∠1=65°,求∠2、∠3、∠4的度数
【典型例题】
【答案与解析】
解:∵ ∠1是∠2的邻补角,∠1=65°,
∴ ∠2=180°-65°=115°
又∵ ∠1和∠3是对顶角,∠2与∠4是对顶角
∴ ∠3=∠1=65°, ∠4=∠2=115°
【总结升华】 (1)两条直线相交所成的四个角中,只要已知其中一个角,就可以求出另外三角;(2)求出∠2后用 “对顶角相等”,求∠3和∠4
【典型例题】
3. 任意画两条相交的直线,在形成的四个角中,两两相配共能组成几对角 各对角存在怎样的位置关系?根据这种位置关系将它们分类。
【典型例题】
【答案与解析】
解:如图,
任意两条相交直线,两两相配共组成6对角,在这6对角中,它们的位置关系有两种:①有公共顶点,一边重合,另一边互为反向延长线;②有公共顶点,角的两边互为反向延长线。
这6对角为∠1与∠2,∠1与∠3,∠1与∠4,∠2与∠3,∠2与∠4,∠3与∠4,其中∠1=∠3,∠2=∠4,∠1+∠2=180°,∠3+∠4=180°,∠1+∠4=180°,∠2+∠3=180°.在位置上∠1与∠3,∠2与∠4是对顶角,∠1与∠2,∠3与∠4,∠l与∠4,∠2与∠3是邻补角。
【总结升华】两条相交的直线,两两相配共组成6对角,这6对角中有:4对邻补角,2对对顶角。
【典型例题】
4.下列语句中,正确的有 ( )
①一条直线的垂线只有一条;
②在同一平面内,过直线上一点有且仅有一条直线与已知直线垂直;
③两直线相交,则交点叫垂足;
④互相垂直的两条直线形成的四个角一定都是直角。
A.0个 B.1个 C.2个 D.3个
【典型例题】
【答案】C
【解析】正确的是:②④
【总结升华】充分理解垂直的定义与性质。
【典型例题】
5.(河北模拟)如图,已知点O在直线AB上,CO⊥DO于点O,若∠1=145°,则∠3的度数为( )
A.35° B. 45° C. 55° D. 65°
【典型例题】
【答案】C
【解析】解:∵∠1=145°,
∴∠2=180°﹣145°=35°,
∵CO⊥DO,
∴∠COD=90°,
∴∠3=90°﹣∠2=90°﹣35°=55°
【总结升华】本题考查了垂线和邻补角的定义;弄清两个角之间的互补和互余关系是解题的关键。
【典型例题】
6.(抚州校级期中)如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )
A.A点 B.B点 C.C点 D.D点
【典型例题】
【思路点拨】根据垂线段最短可得答案。
【答案】A
【解析】解:根据垂线段最短可得:应建在A处,故选:A
【总结升华】此题主要考查了垂线段的性质,关键是掌握从直线外一点到这条直线所作的垂线段最短。
