湘教版七年级上册2代数式课件(共190张PPT)
文档属性
| 名称 | 湘教版七年级上册2代数式课件(共190张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 21:26:29 | ||
图片预览










文档简介
(共190张PPT)
7年级湘教版数学上册第二章教学课件
2.1 用字母表示数
第2章 代数式
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水.两只青蛙两张嘴,四只眼睛,八条腿,两声扑通跳下水.”请接下去……
15只青蛙, 张嘴, 只眼睛, 条腿,
声扑通跳下水……
15
30
60
15
n只青蛙, 张嘴, 只眼睛, 条腿,
声扑通跳下水.
n
2n
4n
n
情景引入
问题1: 2016年我国成功发射了“神州十一号”载人飞船,成功与天宫二号的自动交会对接,形成组合体.飞船在椭圆轨道上环绕地球飞过45周,历时68小时. (1)该飞船绕地球飞行一周需多少分钟?
(2)若绕地球飞行n周,需多久?
(68×60) ÷45= (分钟)
n分钟
一、用字母表示数
问题2: 据中国新闻网2011年9月19日报道:中国工程院院士袁隆平指导的“Y两优2号”百亩①超级杂交稻试验田平均亩产926.6 kg,创中国大面积水稻亩产的最高纪录.
注:① 亩,我国的一种面积单位.1亩≈666.67m2.
杂交水稻之父———袁隆平
(1)根据上面数据完成下表:
亩数 1 1.5 2 2.5 3 …
总产量(kg) 926.6×1 926.6×1.5 …
从表中可知,总产量可用“926.6×亩数”求得.
926.6×2
926.6×2.5
926.6×3
a亩水稻的总产量是
926.6×a(kg).
平均亩产为b kg时,a亩水稻的总产量是a×b(kg).
(2)如果用字母a表示亩数,那么a亩水稻的总产
量是多少?
(3)如果平均亩产为b kg,那么a亩水稻的总产量
是多少?
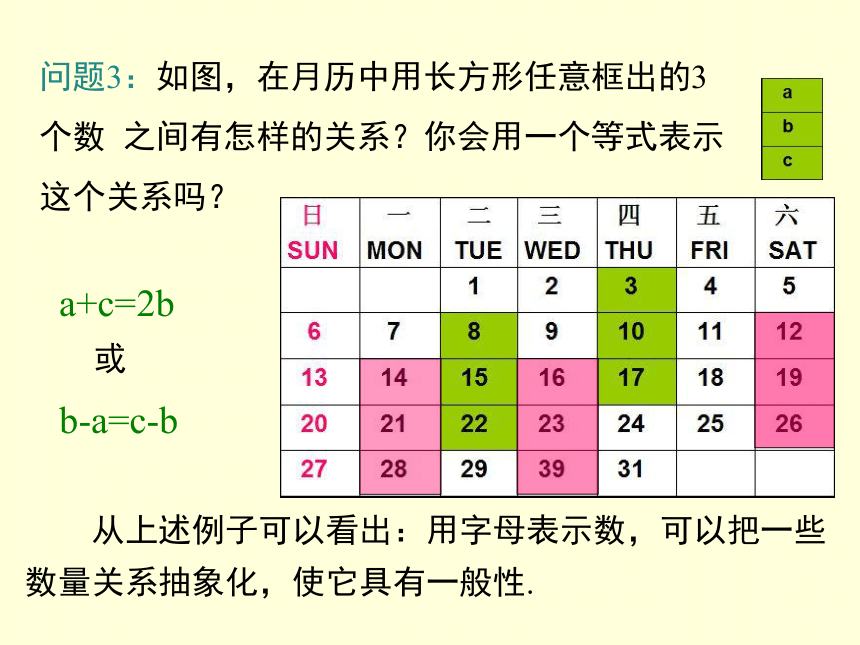
问题3:如图,在月历中用长方形任意框出的3
个数 之间有怎样的关系?你会用一个等式表示
这个关系吗?
a+c=2b
或
b-a=c-b
从上述例子可以看出:用字母表示数,可以把一些数量关系抽象化,使它具有一般性.
5+
8
7
6
3
2
1
进去数字
出来数字
1
2
3
魔 盒
用含有字母的式子表示下列数量:
例1
(2)练习簿的单价为b 元, a本练习簿的总价是 元;
(1)练习簿的单价为a元,100本练习簿的总价是 元;
字母和字母相乘,乘号可以省略不写或用“ · ” 表示.
一般情况下,按26个字母的顺序从左到右来写.
100a
ab
数和字母相乘,可省略乘号,并把数字写在字母的前面
典例精析
(3)练习簿的单价为0.5元,圆珠笔的单价是3.2元,
买a本练习簿和b支笔的总价是 元;
后面带单位的相加或相减的式子要用括号括起来
(0.5a+3.2b)
除法运算写成分数形式,即除号改为分数线
(4)小明的家离学校s千米,小明骑车上学.若每小时行
10千米,则需 时;
带分数与字母相乘时,带分数要写成假分数的形式
(5)若每斤苹果 元,则买m斤苹果需 元;
(6)比a的0.6倍大c的数是 ;
(7)a与b的2倍的积为 .
0.6a + c
2ab
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
字母表示数注意事项:
100×t
100t
nm
mn
nn
n2
1n
n
n÷3
n
3
1
3
1 n
4n
3
总结归纳
判断下列式子书写是否规范,不规范的请改正.
做一做
运算定律 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac+bc
1.用字母表示数的运算律
二、用字母表示运算律和公式
2.用字母表示有关图形的周长和面积计算公式:
名称 图形 用字母表示公式
周长(C) 面积(S)
长方形
三角形
梯形
圆
b
a
a
b
c
h
r
一个正方形盒子的棱长为acm,用含a的式子表示:
盒子的表面积S=____________;
盒子的体积V=____________.
做一做
例2 小莉以5km/ h的速度,走了20km的路程,那么她走了多长时间?如用字母v表示速度,用字母s表示路程,那么她走的时间又如何表示呢?
解: 小莉走20km所花的时间为20÷5=4(h).
若用字母v 表示速度,用字母s 表示路程, 则时间 t = s ÷ v = .
从上述例子看到,用字母表示数,可以统一、简明地表示实际问题中的数量关系.
三、用含字母的式子表示数量关系
1.我们现在讨论的数的范围是有理数,即数a可以是正数,也可以是负数或零,所以a不一定表示正数,-a不一定表示负数.
2.同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
注意:
买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数.
解:买3个篮球、5个排球、2个足球共需要
元.
做一做
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
课堂小结
④小明语文a分,数学b分,那么这两科的平均分为 分.
③一边长为3,这边上的高为h的三角形面积为 .
① n只青蛙 条腿
②同一笼中有鸡a只、兔b只,则共有头 个,脚 只.
1.填空:
课后练习
√
×
√
×
×
×
×
×
×
2.下列代数式中,哪些书写符合要求?
√
3. 如图,有一块长为a,宽为b的长方形铝片,四角各载去一个相同的边长为x的正方形,折起来做成一个没有盖的盒子,则此盒子的容积的表达式应该 ( )
A. V = x2(a-x)(b-x) B. V = x (a-x)(b-x)
C. V = x2(a-2x)(b-2x) D. V = x(a-2x)(b-2x)
解析:由题意可知盒子的底面长为(a-2x),宽为(b-2x),高为x.因此,盒子的容积为V=x(a-2x)(b-2x).故应选D.
D
4.用棋子摆成下列一组图案:
…
( 1 )
( 2 )
( 3 )
① 填写下表:
图案编号 (1) (2) (3) (4) (5) (10) (100)
棋子个数
② 摆第n个图案需要____个棋子.
3
6
9
12
15
30
300
3n
2.2 列代数式
今年暑假,老师从深圳出发,随旅游团到北京旅游.虽然做了充分准备,但是还遇到了许多数学难题.希望大家能帮帮老师!
情景引入
深圳的气温为 x 摄氏度,北京的气温比深圳低4摄氏度,北京的气温为 摄氏度.
游程1:准备
深圳到北京的距离是s千米,高铁的速度为300千米/小时,到达北京需 小时.
游程2:出发
售票处
……
门票价格
成人:每人60元 学生:每人20元
我们有a个成人, b个学生,买门票需付 ________ 元钱.
游程3:买票
太和殿占地呈长方形,长m米,宽n米太和殿占地面积有多少平方米呢
平方米
游程4:参观
珍宝馆陈列厅呈正方形,边长为a米.地面积有多少平方米呢
平方米
游程4:参观
珍宝馆内有一金嵌珍珠宝石塔,宝石塔外边是一个长方体的玻璃罩,它的长、宽、高分别是3、p、q米.此玻璃罩的体积为多少?
立方米
游程4:参观
像 的式子都是用运算符号把数与字母连接而成的,叫做代数式.
一、代数式的概念
概念学习
(运算符号包括+、-、×、÷、乘方)
判断下列式子哪些是代数式,哪些不是.
(3) x=2 (4)13
( √ )
( √ )
( × )
( × )
( √ )
(5) (6) x+2>3
(1) a2+b2 (2)
( × )
练一练
注意:(1)代数式中不含表示关系的符号
(“=”“>”“<”“≥”“≤”“≠”).
(2)单独的一个数或字母也是代数式.
例1 用代数式表示:
(1)a的7倍与2b的差;
(2)x,y两数的平方和减去两数积的2倍;
(3)a的倒数与b的和.
解:
(1) ;
(2) ;
(3) .
典例精析
(1)已知铅笔每支x元,练习本每本y元.小明买铅笔5支,练习本6本,需多少元?
二、列代数式
例2 列代数式:
(5x+6y)元;
(2)小兰家距学校5km.她步行的速度是vkm/h,而骑自行车比步行快10km/h.她骑自行车的速度是多少?她骑自行车从家到学校需多长时间?
小兰骑自行车的速度是(v+10)km/h,从家到学校需
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
方法归纳
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度.
例3
分析:顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是 km/h,逆水行驶的速度是 km/h.
(2)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
(3)右 下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
解:(2)三角尺的面积是( )cm2.
(3)这所住宅的建筑面积是( )m2.
列式要点:
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
方法归纳
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
练一练
(3)有两片棉田,一片有m hm2 (公顷,1 hm2 =104 m2 ),平均每公顷产棉花a kg;另一片有n hm2 ,平均每公顷产棉花b kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a mm,小正方形的边长是b mm,用式子表示剩余部分的面积.
代数式10x+5y可以表示什么?
如果用x表示1支铅笔的价格,用y表示1本练习本的价格,那么10x+5y可以表示_______________________的总钱数;
想一想:
10支铅笔与5本练习本
三、解释代数式所表示的实际意义
例4 下列代数式可以表示什么?
(1)2a-b;(2)2(a-b).
解:(1)若篮球的单价是a元,足球的单价是b元,2a-b可表示为卖两个篮球比买一个足球多花(2a-b)元;
(2)若某商店的一台学习机的售价为a元,进价为b元,2(a-b)可表示为卖出两台学习机给商店盈利2(a-b)元.
代数式
根据实际问题列代数式
代数式的概念
解释解释代数式所表示的实际意义
判别代数式
代数式的书写要求
课堂小结
(1)5箱苹果重m kg,每箱重 kg ;
(2)一个数比a的2倍小15,则这个数为 ;
(3)全校学生总数是x,其中女生占总数52%,则女生人数是 ,男生人数是 ;
(4)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共有
本;
1.用式子表示下列数量:
课后练习
2.判断下列式子哪些是代数式,哪些不是
(5)3×(4 -5) (6) 3×4 -5 =7
(7)x-1≤0 (8) x+2>3
(9)10x+5y=15 (10) +c
(1)a2+b2 (2)
(3)13 (4)x=2
(1)(2)(3)(5)(10)是代数式;
(4)(6)(7)(8)(9)不是代数式.
3.说出下列代数式的意义:
(1)圆珠笔每支售价a元,练习簿每本售价b元,那么,3a+4b表示什么?
(2)长方形的长、宽分别为a、b,那么a(b+1)表示什么?
解:(1) 3支圆珠笔与4本练习簿的总价格;
(2)长为a,宽为b+1的长方形的面积.
2.3 代数式的值
据报纸记载,一位医生研究得出由父母身高预测子女成年后身高的公式:儿子身高是由父母身高的和的一半,再乘以1.08;女儿的身高是父亲身高的0.923倍加上母亲身高的和再除以2.
情景引入
(1)已知父亲身高是a米,母亲身高是b米,试用代数式表示儿子和女儿的身高;
(2)五年级女生小红的父亲身高是1.75米,母亲的身高是1.62米;六年级男生小明的父亲的身高是1.70,母亲的身高是1.62,试预测成年以后小明与小红谁个子高?
一、求代数式的值
合作探究
数值转换机
输入 -2 -1/2 0 0.26 1/3 5/2 4.5
机器1的输出结果
机器2的输出结果
输入x
输入x
输出
输出
×6
-3
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
×6
-3
议一议
n 1 2 3 4 5 6 7 8
5n+6
n2
11
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
逐渐增大
n2 先超过
填写下表,并观察下列两个代数式的值的变化情况.
例1 (1)当x=-3时,求 的值;
(2)当a=0.5,b=-2时,求 的值.
解:(1)当x=-3时,
(2)当a=0.5,b=-2时,
典例精析
针对训练
1.当x=-3,y=2时,求下列代数式的值:
解:
当x=-3,y=2时,
2.
解:
方法归纳
1.求代数式的值的步骤:
(1)写出条件:当……时
(2)抄写代数式
(3)代入数值
(4)计算
解:当x=2,y=-3时,
x(x-y)
= 2×[2-(-3)]
=2 ×5
=10
当x=2,y=-3时,求代数式x(x-y)的值.
(1)代入时,要“对号入座”,避免代错字母,其他符号不变.
(2)代数式中,代入数值以后原来省略的乘号一定要还原.
(3)若字母的值是负数或分数,将字母的值代入代数式时,应加上括号,原来的数字和运算符号都不能改变.
2.在代入数值时应注意:
例2 已知x-2y=3,则代数式6-2x+4y的值.
解:6-2x+4y=6-2(x-2y),
因为x-2y=3,将其代入上式中,可得
6-2x+4y=6-2×3=0.
相同的代数式可以看作一个字母——整体代入
典例精析
【变式】已知 则 的值是多少?
解:
由
可得
将
代入上式:
练一练
当x=1时,代数式 ,当x=-1时,该代数式的值是多少?
解:将x=1代入代数式,得a+b=2018,当x=-1时,
二、间接(或根据公式)求代数式的值
例3 我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长,S为图形的面积,L是边界上的格点数,N是内部格点数,则有 . 请根据此方法计算图中四边
形ABCD的面积.
解:由图可知边界上的格点数L=8,
内部格点数N =12,
所以四边形ABCD的面积为
例4 堤坝的横截面是梯形,测得梯形上底为a=18m,下底b=36m,高h=20m,求这个截面的面积.
a
b
h
解:梯形面积公式为:
将a=18m,b=36m,h=20m代入上面公式,得
答:堤坝的横截面积是
a
b
h
代数式的值
概念
应用
用数字代替代数式中的 ,
按照代数式中的 关系计算得出的结果叫做代数式的值.
运算
字母
直接代入求值
列代数式求值
整体代入求值
步骤
1.代入
2.计算
课堂小结
1.当a=2,b=1,c=3时代数式c-(c-a)(c-b)的值是( )
5.已知a+b=3 , 则4–a-b=______.
A.1 B.2 C.3 D.4
A
2.如果2a+3b=5,那么4a+6b-7=__.
3
3.已知a+b=5,ab=6 ,则ab-(a+b)=___.
4. 当a=-2,b=-1时,1-|b-a|=_____.
6.已知2x2+3x+7=8 , 则4x2+6x-9=______.
1
1
0
-7
课后练习
7.某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
解:(1)该旅游团应付的门票费是(10x+5y)元.
(2)把x=37,y=15代入代数式,得
10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
8.现代营养学家用身体质量指数衡量人体胖瘦程度,这个指数等于人体质量(千克)与人体身高(米)平方的商.对于成年人来说,身体质量指数在20~25之间,体重适中;身体质量指数低于18,体重过轻;身体质量指数高于30,体重超重.
(1)设一个人的体重为w(千克),身高为h(米),求他的身体质量指数.
解:他的身体质量指数为
(2)张老师的身高是1.75米,体重是65千克,他的体重是否适中?
解:(2)把w=65,h=1.75代入代数式,得
由于21在20到25之间,因此,他的体重适中.
2.4 整 式
这两个式子都是代数式,那么不同的代数式之间又有哪些区别和联系呢?
某学校的操场如图所示,由一个长方形和两个半圆组成.
(2)整个操场的面积是多少?
(1)两个半圆的面积是多少?
情景引入
一、单项式的相关概念
用含有字母的式子填空
1. 棱长为a的正方形的表面积为____ ;体积为_ __.
3. 一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
6a2
a3
4. 一个圆的半径是r cm,它周长是 cm.
2πr
思考: 6a2,a3,2.5x,vt,2πr 以上各式中运算
有什么共同特点?
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示字母与数字、字母与字母的积).
这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
例如:像-2,a,-b, 等是单项式.
注意:像 , , 等不是单项式.
为什么?
概念学习
练一练
下列式子中哪些是单项式
√
√
√
√
√
√
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
方法总结
思考:单项式中的数字和字母各有何意义呢
a
2
6
系数
次数
__
1
5
=-
ab
系数
定义:单项式中数与字母相乘,通常把数字因数
叫做系数;所有字母的指数的和叫做这个
单项式的次数.
二次
次数
典例精析
练一练
1.判断下列说法是否正确:
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 .( )
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
(1)每包书有12册,n包书有_____册;
(2) 底边长为a,高为h的三角形的面积是_____;
(3) 一个长方体的长和宽都是a,高为h,它的体积是_____;
(4)一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为____;
(5)一个长方形的长为0.9,宽为a,面积是____.
1
2.用单项式填空,并指出它们的系数和次数:
12n
0.9a
0.9a
一次
二次
三次
一次
一次
1.单项式的系数:单项式中的数字因数.若一个单项式只含有字母因数,那么它的系数就是1或-1;若单项式是单独一个数,则系数就是它本身.
2.单项式的次数应是该单项式中所有字母的指数和,与系数的指数没关系,如24x2y3的次数是5,而不是9;单独一个数的次数是0.
3.不要把π当成字母.
归纳总结
二、多项式及其有关概念
(1)若三角形的三条边长分别为a、b、c,则三角形的周长是________;
(2)某班有男生x人,女生21人,这个班的学生一共有
_____人;
(3)如图,三角尺的面积为 .
a+b+c
(x+21)
列代数式:
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
议一议
单项式
单项式
+
上述几个式子都是两个或者多个单项式相加的形式.
a+b+c
(x+21)
多项式有关概念
1.几个单项式的和叫做多项式.
2.在多项式中,每个单项式叫做多项式的项.
3.不含字母的项叫做常数项.
4.多项式里次数最高项的次数就是多项式的次数.
单项式与多项式统称为整式.
多项式:
常数项
次数
概念学习
例2 说出下列多项式的次数和常数项:
解:
(1)
(2)
(3)
(1) 的次数是1,常数项是-3.
(2) 的次数是3,常数项是-4;
(3) 的次数是2,常数项是-9.
例3 下列整式中哪些是单项式?哪些是多项式?是
单项式的指出系数和次数,是多项式的指出项和次数:
x
32t3
1
32
1
3
0
6
3
解:
1
4
2
要点归纳:
(1)多项式的各项应包括它前面的符号
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的
(4)一个多项式的最高次项可以不唯一
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号
例4 已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
【变式】若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
解:∵关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,
∴m=0,n-1=0,
则m=0,n=1.
做一做
1.多项式x2+y-z是单项式___,___,___的
和,它是___次___项式.
2.多项式3m3-2m-5+m2的常数项是____,二次
项是_____,二次项的系数是_____.
x2
y
-z
二
三
-5
m2
1
二、多项式的应用
例5 如图所示,用式子表示圆环的面积.当 cm,
cm时,求圆环的面积( 取 ).
解:外圆的面积减去内圆的面积就是圆环
的面积,所以圆环的面积是 .
这个圆环的面积是
cm2 .
当 cm , cm 时,
圆环的面积是
做一做
(2) , 分别表示梯形的上底和下底, 表示
梯形的高,则梯形面积 = ,当
=2 cm, =4 cm, =5 cm时, = cm 2 .
1.(1) , 分别表示长方形的长和宽,则长方形的周长
= ,面积 = ,当 =2 cm,
=3 cm时, = cm, = cm 2 ;
2.小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
(1)窗户中能射进阳光的部分的面积分别是多少?
a
b
a
b
(2)你能指出其中的单项式或多项式吗?它们的次数分别是多少?
都是多项式,次数都是2次
整式
单项式
多项式
由数与字母的积组成的代数式叫单项式
单独一个字母或一个数也是单项式
单项式中,与字母相乘的数叫做单项式的系数
单项式中所有字母的指数的和叫做这个单项式的次数
由几个单项式的和组成的代数式叫做多项式
不含字母的项叫做常数项
多项式中次数最高的项的次数叫做这个多项式的次数
组成多项式的每个单项式叫做多项式的项
课堂小结
1.下列式子中,哪些是单项式?哪些是多项式?哪些是整式?
3x,2x-1, ,-ab,-5, -1,3m-4n+m2n.
课后练习
2.判断正误:
(1)多项式-x2y+2x2-y的次数2.( )
(2)多项式 - -a+3a2的一次项系数是1.( )
(3)-x-y-z是三次三项式.( )
3.一个关于字母x的二次三项式的二次项系数为4,一次项系数为1,常数项为7,则这个二次三项式为___.
×
×
×
4x2+x+7
4.如图,某居民小区有一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在此空地的四个顶点处各修建一个半径为a米的扇形花台,在花台内种花,其余种草.如果建造花台及种花费用每平方米为100元,种草费用每平方米为50元.那么美化这块空地共需多少元?
解:花台面积和为πa2平方米,
草地面积为(2ab-πa2)平方米.
所以需资金为[100πa2+50(2ab-πa2)]元.
2.5 整式的加法和减法
第1课时 合并同类项
生活中,我们常常把具有相同特征的事物归为一类 ,请同学们给下列物品分类.
蔬菜
水果
情景引入
观察超市货物摆放
观察药店药品摆放
如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢
储蓄罐
一、同类项的辨别
-7a2b
问题1 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的次数的特征将这些小白兔分到三个不同的栅栏里吗?
8n
3ab2
2a2b
6xy
5n
-3xy
-ab2
-7a2b
问题2 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到四个不同的栅栏里吗?这些被归为同一类的兔子有什么相同的特征?
8n
3ab2
2a2b
6xy
5n
-3xy
-ab2
同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.
(1)两个相同:字母相同;相同字母的次数相同;
(2)两个无关:与系数大小无关;与字母顺序无关;
(3)所有的常数项都是同类项.
说明:
知识要点
游戏一
游戏二
(3)-3pq与3qp
(1)2x2y与-3x2y
(2)2abc与2ab
(4) -4x2y与5xy2
先判断每一组是否是同类项,若不是的,请为前者配一个.
√
√
3abc
x2y
×
×
总结归纳
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
典例精析
例1 (1)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
(2)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:(1)根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
二、合并同类项
x
x
x
2
+ 3
=
5
=
3
-
a2bc
a2bc
a2bc
2
奇妙的替换
你还有其他方法解释吗?
利用乘法分配律可得
(2+3)
x
x
2
+ 3
=
x
=
3
a2bc
a2bc
a2bc
-2
(3-2)
= 5x
= a2bc
把同类项合并成一项叫做合并同类项.
解:
(1)
(2)
例2. 合并下式中的同类项:
(1) (2)
解:
(1)
(1)
1.将同类项在底下划线标出;
2.运用加法的交换律和结合律,把同类项放在一起;
3.合并同类项.
注意:对于不同的同类项,分别用不同的线标出.
例3. 合并下式中的同类项:
(1)
(2)
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
总结归纳
系数相加,字母及其指数不变
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
下列合并同类项对吗?不对的,说明理由.
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
说一说
×
√
×
×
×
√
你会计算吗?
⑴ 100t-252t ;
⑵ 3a+2b-5a-b ;
⑶ -4ab+8-2b2-9ab-8 .
试一试
答案:⑴-152t ; ⑵-2a+b ; ⑶-13ab-2b2.
先分组,再合并
练一练
合并同类项:
(1)6x+2x2-3x+x2+1;
(2)-3ab+7-2a2-9ab-3.
解:(1)原式=(6x-3x)+(2x2+x2)+1
=3x+3x2+1
(2)原式=(-3ab-9ab)-2a2+(7-3)
=-12ab-2a2+4
例4 (1)求多项式 的值,
其中x = ;
(2)求多项式 的值,
其中a= ,b=2,c=-3.
分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.
解:(1)
当x = 时,原式=
(2)
当a= ,b=2,c=-3时,原式=1.
议一议
在不知道a,b的情况下,能否求出“7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2”的值,若能,请求出数值;若不能,请说明理由.
解:能.理由如下:
化简7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2
=(7a2-4a2-3a2)+(-5b2+b2+4b2)+(3a2b-3a2b)-2
=-2,
所以无论a,b取任何值,代数式的值都为2.
例5 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克.所以摊主说得没有道理,这样做小明奶奶吃亏了.
合并同类项的方法——“一加二不变”
同类项的概念
与系数无关
与所含字母的顺序无关
两无关
两同
相同字母的指数相同
所含字母相同
合并同类项
课堂小结
一、填空题.
1.如果5x2y与xmyn是同类项,那么 m=____,n=____.
2.合并同类项:
(1)-a-a-2a=________.
(2)-xy-5xy+6yx=________.
(3)0.8ab2-a2b+0.2ab2=_______.
2 1
-4a
0
ab2-a2b
课后练习
二、选择题.
3.下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
4.下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
C
A
课后练习
三、合并下列各式中的同类项:
5.-7mn+mn+5nm;
6.3a2b-4ab2-4+5a2b+2ab2+7.
四、求下列各式的值:
7.3x2-8x+2x3-13x2+2x-2x3+3,其中x=-1.
8.a2b-6ab-3a2b+5ab+2a2b,其中a=0.1,b=0.01.
-mn
8a2b-2ab2+3
-10
1
2
-0.001
2.5 整式的加法和减法
第2课时 去括号
同学们还记得用火柴棒搭正方形时,怎样计算所需要的火柴棒的根数吗?拿出准备好的火柴自己搭一下,然后再按如下做法搭.
第一个正方形用4根,每增加一个正方形增加3根,那么搭x个正方形就需要火柴棒
根.
[4+3(x-1)]
情景引入
把每一个正方形都看成是用4根火柴棒搭成的,然后再减多算的根数,得到的代数式是 .
[4x-(x-1)]
(3x+1)
一、去括号法则
合作探究
搭x个正方形,用的方法不一样,列出的式子不同,但所用火柴棒的根数一样,用数学知识来说明它们为什么相等呢?
代数式4+3(x-1),有括号,用乘法分配律可以把3乘到括号里,得4+3x-3,而4与-3是同类项可以合并,这时,代数式就变为3x+1.
即4+3(x-1)
=4+3x-3 (乘法分配律)
=3x+1. (合并同类项)
代数式4x-(x-1)可以看作是4x+[-(x-1)],而-(x-1)可写成(-1)(x-1),所以4x-(x-1)就等于4x-x+1,合并同类项得3x+1.
从而得出结论:这三个代数式是相等的.
即4x-(x-1)
=4x+(-1)(x-1)
=4x-x+1
=3x+1.
议一议
观察比较两式等号两边画横线的变化情况.
(1)4+ 3(x-1) =4+ 3x-3 =3x+1;
(2)4x -(x-1) =4x -x+1 =3x+1.
去括号前后,括号里各项的符号有什么变化?
思考:
括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
去括号法则:
例1 计算:
(1) (5x-1)+(x-1) ; (2) (2x+1)-(4-2x).
解:
(1) (5x-1)+(x-1)
=5x-1+x-1
=6x-2;
(2) (2x+1)-(4-2x)
=2x+1-4+2x
=4x-3.
括号前是“+”号,运用加法结合律把括号去掉,括号里各项的符号都不改变.
括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项都符号都要改变.
典例精析
【归纳总结】
(1)去括号时,不仅要去掉括号,还要连同括号前面的符号一起去掉.
(2)去括号时,首先要弄清括号前是“+”号还是“-”号.
(3)注意法则中的“都”字,变号时,各项都变号;不变号时,各项都不变号.
(4)当括号前有数字因数时,应运用乘法分配律运算,切勿漏乘.
(5)出现多层括号时,一般是由里向外逐层去括号.
判断正误
(1)3(x+8)=3x+8
(2)-3(x-8)=-3x-24
(4)-2(6-x)=-12+2x
(3)4(-3-2x)=-12+8x
错
3x+3×8
错因:分配律,漏乘3.
错
-3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
对
错
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
-12-8x
做一做
二、利用去括号化简求值
练一练
先化简,再求值:3x2+(2x2-3x)-(-x+5x2),其中x=314.
解:原式=3x2+2x2-3x+x-5x2=-2x.
当x=314时,原式=-2×314=-628.
例3 两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1)2小时后两船相距多远
(2)2小时后甲船比乙船多航行多少千米
三、去括号化简的应用
解:顺水速度=船速+水速=(50+a)km/h,
逆水速度=船速-水速=(50-a)km/h.
(1)2小时后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.
(2)2小时后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
括号前面是“+”号,里面各项不变号.
括号前面是“-”号,里面各项全变号.
乘系数
去括号
合并同类项
④代入求值
去括号法则
解题步骤
去括号
课堂小结
1.化简m-n-(m+n)的结果是( )
A.0 B.2m C.-2n D.2m-2n
2.化简4x-4-(4x-5)=________.
3.化简2(2x-5)-3(1-4x)=________.
4.三角形的第一边长是(2a+b)cm,第二边长是2(a+b)cm,第三边长比第二边长短b cm,则这个三角形的周长是________cm.
C
1
16x-13
(6a+4b)
课后练习
5.化简下列各式:
(1)8m+2n+(5m-n); (2)(5p-3q)-3( ).
解:
6.已知2xmy2与-3xyn是同类项,计算m-(m2n+3m-4n)+(2nm2-3n)的值.
答案:2
7.有理数a,b,c在数轴上位置如图,化简代数式│a│-│a+b│+│c-a│+│b-c│
答案:a-2c
8.某商店有一种商品每件成本a元,原来按成本增加b元定出售价,售出40件后,由于库存积压,调整为按售价的80%出售,又销售了60件.
(1)销售100件这种商品的总售价为多少元?
(2)销售100件这种商品共盈利多少元?
解:(1)根据题意得:40(a+b)+60(a+b)×80%=88a+88b(元),
则销售100件这种商品的总售价为(88a+88b)元;
(2)根据题意得:88a+88b-100a=-12a+88b(元),
则销售100件这种商品共盈利(-12a+88b)元.
2.5 整式的加法和减法
第3课时 整式的加减
任意写一个两位数
交换它的十位数字与个位数字,又得到一个数
两个数相加
小组游戏
重复几次看看,谁能先发现这些和有什么规律?对于任意一个两位数都成立吗?
10a+b+10b+a=11a+11b=11(a+b)
一、整式的加减
合作探究
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: .交换这个两位数的十位数字和个位数字,得到的数是: .将这两个数相加:
+ =
.
10a+b
10b+a
(10a+b)
(10b+a)
结论:
这些和都是11的倍数.
做一做
任意写一个三位数
交换它的百位数字与个位数字,又得到一个数
两个数相减
你又发现什么了规律?
原三位数728,百位与个位交换后的数为827,由728 -827= -99.你能看出什么规律并验证它吗?
设原三位数为100a+10b+c,百位与个位交换后的数为100c+10b+a,它们的差为:
(100a+10b+c)-( 100c+10b+a)
= 100a+10b+c-100c-10b-a
=99a-99c
=99(a-c)
举例:
任意一个三位数可以表示成100a+10b+c
议一议
在上面的两个问题中,分别涉及了整式的什么运算?说说你是如何运算的?
去括号、合并同类项
八字诀
整式的加减运算
解:
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
典例精析
例1 求整式 与 的和.
解:根据题意,得
去括号
合并同类项
去括号
合并同类项
例2 求多项式 与多项式 的和与差.
练一练
二、整式加减的应用
解:
当x=1,y=-2时,
例3 先化简,再求值.
,其中x=1,y=-2.
(1)整式的加减运算重点注意去括号时的符号、系数的处理,不要把符号弄错,不要漏乘括号外的系数;
(2)整式的化简求值题,能够化简的最好先化简,尽量不要直接把字母的值代入计算.
方法归纳
的值,
其中
先将式子化简,再代入数值进行计算
解:
当 时,
原式
→去括号
→合并同类项
﹜
将式子化简
练一练
例4 如图,正方形的边长为x,用整式表示图中阴影部分的面积,并计算当x=4m时阴影部分的面积( 取3.14).
x
x
解:阴影部分的面积为:
当x=4m 时,阴影部分的面积为:
解决整式加减的实际应用题时,先要把具体量用代数式表示出来,然后根据整式加减运算的法则、步骤进行计算.
注意最后结果是几个单项式的和的形式,且要带单位时,要整体加括号.
方法归纳
例5 做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
解:小纸盒的表面积是( )cm
2
大纸盒的表面积是( )cm
2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm )
2
a
b
c
1.5a
2b
2c
2ab
+2bc
+2ca
6ab
+ 8bc
+ 6ca
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)- (2ab+2bc+2ca)
=6ab+8bc+6ca- 2ab-2bc-2ca
=4ab+6bc+4ca(cm )
2
(2)做大纸盒比小纸盒多用料多少平方厘米?
小纸盒的表面积是(2ab+2bc+2ca)cm
大纸盒的表面积是(6ab+8bc+6ca)cm
2
2
通过上面的学习,你能得到整式加减的运算法则吗?
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
想一想
例6 已知A=-6x2+4x,B=-x2-3x,C=5x2-7x+1,小明和小白在计算时对x分别取了不同的数值,并进行了多次计算,但所得A-B+C的结果却是一样的.你认为这可能吗?说明你的理由.
理由:A-B+C
=(-6x2+4x)-(-x2-3x)+(5x2-7x+1)
=-6x2+4x+x2+3x+5x2-7x+1
=1.
解:可能.
由于结果中不含x,所以不论x取何值,A-B+C的值都是1.
整式加减的步骤
整式加减的应用
整式的加减
去括号
合并同类项
课堂小结
8a
2x3-xy2
解:(3x2-2x+1)-2(x2-x)-x2=3x2-2x+1-2x2+2x-x2=1
3.计算(3x2-2x+1)-2(x2-x)-x2的值,其中x=-2,小明把“x=-2”错抄成“x=2”,但他的计算结果仍是正确的,这是怎么回事?说明理由.
由于结果中不含x,所以不论x取何值,原式的值都是1.
课后练习
4. 计算
(1)- ab3+2a3b- a2b-ab3- a2b-a3b
(2)(7m2-4mn-n2)-(2m2-mn+2n2)
(3)-3(3x+2y)-0.3(6y-5x)
(4)( a3-2a-6)- ( a3-4a-7)
答案:(1)
5. 一种笔记本的单价是x元,圆珠笔的单价是y元.
小红买这种笔记本3本,买圆珠笔2支;小明买这种
笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,
小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
你还能有其他解法吗?
另解:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)+(2y+3y)
=7x+5y
分别计算笔记本和圆珠的花费.
6.某公司计划砌一个形状如下图(1)的喷水池,后有人建议改为如下图(2)的形状,且外圆直径不变,只是担心原来备好的材料不够,请你比较两种方案,哪一种需用的材料多(即比较两个图形的周长)?若将三个小圆改为n个小圆,又会得到什么结论?
思路点拨
设大圆半径为R,小圆半径依次为r1,r2,r3,
则图(1)的周长为4πR,图(2)的周长为
2πR+2πr1+2πr2+2πr3=2πR+2π(r1+r2+r3),
因为2r1+2r2+2r3=2R,所以r1+r2+r3=R,因此图(2)
的周长为2πR+2πR=4πR.
这两种方案,用材料一样多,将三个小圆改为n个
小圆,用料还是一样多.
R
2r1+2r2+2r3=2R
小结与复习
第2章 代数式
要点梳理
一、整式的有关概念
1.代数式:把数与表示数的字母用运算符号连接而成的式子叫做代数式.单独一个字母或一个数也是代数式.
2.代数式的值:把代数式里的字母用数代入,计算后得出的结果叫做代数式的值.
3.单项式:由数或字母的____组成的代数式叫做单项式,单独的一个字母或一个数也是单项式.
4.单项式的系数:单项式中,与字母相乘的数做单项式的系数.
积
5.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
6.多项式:由几个单项式的____组成的代数式叫做多项式.
7.多项式的项:组成多项式的每个单项式叫做多项式的项,其中不含字母的项叫做常数项.
8.多项式的次数:多项式中次数最高的项的次数,叫做这个多项式的次数.
9.整式:________________统称整式.
和
单项式与多项式
二、同类项、合并同类项
1.同类项:所含字母________,并且相同字母的指数也分别______的项,乘它们为同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.
3.合并同类项时,同类项的系数相加,字母和字母的指数不变.
【注意】
(1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项;
(2)只有同类项才能合并,如x2+x3不能合并.
相同
相同
三、去括号的法则:
(1)如果括号前面是“+”号,运用加法的结合律把括号去掉,原括号里各项的符号都不变.
(2)如果括号前面是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要改变.
四、整式加减
一般地,几个整式相加减,如果有括号就先________,然后再_____________.
去括号
合并同类项
例1:在式子3m+n, -2mn, p, , 0中,单项式的个数是( )
A.3 B.4 C.5 D.6
考点讲练
考点一 整式的有关概念
A
√
√
√
【易错警示】单项式的次数和系数、多项式的次数和项是容易混淆的概念,需辨别清楚.
针对训练
1.在式子x-2,0,-a,-3x2y, , 中,单项式共有( )
A.5个 B.4个 C.3个 D.2个
C
√
√
√
2.代数式 的系数是________,次数是________ .
3
考点二 同类项
例2 若3xm+5y2与x3yn的和是单项式,求mn的值.
【分析】 根据同类项的定义,可知x的指数和y的
指数分别相等.
解:m+5=3,得m=-2,n=2.故mn=(-2)2=4.
【方法技巧】根据同类项的概念,相同字母的指数相等.列方程式解此类题的一般方法.
针对训练
3.若5x2 y与x m yn是同类项,则m=( ) ,n=( )
若5x2 y与x m yn的和是单项式,则m=( ) , n=( )
2
1
2
1
只有同类项才能合并成一项
考点三 去括号
例3 已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1)A+B;(2)2B-2A.
解:(1)A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2)2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
方法总结
去括号是应注意:
(1)括号前是“-”号,去括号时括号里的各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
针对训练
4.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
考点四 整式的加减运算与求值
例4 已知
求3A+2B-36C的值,其中x=-6.
解:
当x=-6时,-x+24=-(-6)+24=30.
方法总结
在求多项式的值时,一般情况下是先化简,然后再把字母的值代入化简后的式子中求值,化简的过程就是整式运算的过程.
5. 已知式子x2+3x+5的值为7,那么式子3x2+9x-2的值是( )
A.0 B.2 C.4 D.6
针对训练
【解析】已知x2+3x+5=7,目前没办法解出x.可以考虑把x2+3x当做一个整体,于是可得x2+3x=2.
因此3x2+9x-2=3(x2+3x)-2=3×2-2=6-2=4.故选A.
A
运用整体思想
考点五 与整式的加减有关的探索性问题
例5 甲对乙说:“有一个游戏,规则是:任意想一个数,把这个数乘以2,结果加上8,再除以2,最后减去所想的数,此时我就知道结果”请你说说甲为什么会知道结果.
解:设所想的数为n,
则(2n+8)÷2-n=n+4-n=4.
因为结果是常数4,
所以与所想的数无关,因此甲能知道结果.
方法总结
解决此类问题的关键是根据游戏规则正确列出式子,并化简.
针对训练
6. 学习了有理数的运算后,小明设计了一种计算程序,如图所示,当小明输入-6时,则输出值y=________.
36
7. 观察下列图形:它们是按一定规律排列的,依照此规律,第2016个图形中共有________个五角星.
6049
【解析】可以发现每个图形的五角星个数都比前面一个图形的五角星个数多3个.由于第1个图形的五角星个数是3×1+1,所以第n个图形的五角星个数是3n+1,故第2016个图形五角星个数是3×2016+1=6049.
课堂小结
整 式 的 加 减
用字母表示数
单项式:
多项式:
去括号:
同类项:
合并同类项:
整式的加减:
系数、次数
项、次数、常数项
定义、“两相同、两无关”
定义、法则、步骤
法 则
步 骤
整 式
7年级湘教版数学上册第二章教学课件
2.1 用字母表示数
第2章 代数式
“一只青蛙一张嘴,两只眼睛,四条腿,一声扑通跳下水.两只青蛙两张嘴,四只眼睛,八条腿,两声扑通跳下水.”请接下去……
15只青蛙, 张嘴, 只眼睛, 条腿,
声扑通跳下水……
15
30
60
15
n只青蛙, 张嘴, 只眼睛, 条腿,
声扑通跳下水.
n
2n
4n
n
情景引入
问题1: 2016年我国成功发射了“神州十一号”载人飞船,成功与天宫二号的自动交会对接,形成组合体.飞船在椭圆轨道上环绕地球飞过45周,历时68小时. (1)该飞船绕地球飞行一周需多少分钟?
(2)若绕地球飞行n周,需多久?
(68×60) ÷45= (分钟)
n分钟
一、用字母表示数
问题2: 据中国新闻网2011年9月19日报道:中国工程院院士袁隆平指导的“Y两优2号”百亩①超级杂交稻试验田平均亩产926.6 kg,创中国大面积水稻亩产的最高纪录.
注:① 亩,我国的一种面积单位.1亩≈666.67m2.
杂交水稻之父———袁隆平
(1)根据上面数据完成下表:
亩数 1 1.5 2 2.5 3 …
总产量(kg) 926.6×1 926.6×1.5 …
从表中可知,总产量可用“926.6×亩数”求得.
926.6×2
926.6×2.5
926.6×3
a亩水稻的总产量是
926.6×a(kg).
平均亩产为b kg时,a亩水稻的总产量是a×b(kg).
(2)如果用字母a表示亩数,那么a亩水稻的总产
量是多少?
(3)如果平均亩产为b kg,那么a亩水稻的总产量
是多少?
问题3:如图,在月历中用长方形任意框出的3
个数 之间有怎样的关系?你会用一个等式表示
这个关系吗?
a+c=2b
或
b-a=c-b
从上述例子可以看出:用字母表示数,可以把一些数量关系抽象化,使它具有一般性.
5+
8
7
6
3
2
1
进去数字
出来数字
1
2
3
魔 盒
用含有字母的式子表示下列数量:
例1
(2)练习簿的单价为b 元, a本练习簿的总价是 元;
(1)练习簿的单价为a元,100本练习簿的总价是 元;
字母和字母相乘,乘号可以省略不写或用“ · ” 表示.
一般情况下,按26个字母的顺序从左到右来写.
100a
ab
数和字母相乘,可省略乘号,并把数字写在字母的前面
典例精析
(3)练习簿的单价为0.5元,圆珠笔的单价是3.2元,
买a本练习簿和b支笔的总价是 元;
后面带单位的相加或相减的式子要用括号括起来
(0.5a+3.2b)
除法运算写成分数形式,即除号改为分数线
(4)小明的家离学校s千米,小明骑车上学.若每小时行
10千米,则需 时;
带分数与字母相乘时,带分数要写成假分数的形式
(5)若每斤苹果 元,则买m斤苹果需 元;
(6)比a的0.6倍大c的数是 ;
(7)a与b的2倍的积为 .
0.6a + c
2ab
① 数与字母、字母与字母相乘时省略乘号,数与字母相乘时数字在前;
② 出现多个字母时,字母按照26个字母顺序排列;
③ 相同字母相乘时应写成幂的形式;
④ 1或-1与字母相乘时,1通常省略不写;
⑤ 式子中出现除法运算时,一般按分数形式来写,带分数与字母相乘时,把带分数化成假分数.
字母表示数注意事项:
100×t
100t
nm
mn
nn
n2
1n
n
n÷3
n
3
1
3
1 n
4n
3
总结归纳
判断下列式子书写是否规范,不规范的请改正.
做一做
运算定律 字母表示
加法交换律
加法结合律
乘法交换律
乘法结合律
乘法分配律
a + b = b + a
(a + b) +c= a +(b + c)
ab = ba
(ab)c = a(bc)
(a + b) c = ac+bc
1.用字母表示数的运算律
二、用字母表示运算律和公式
2.用字母表示有关图形的周长和面积计算公式:
名称 图形 用字母表示公式
周长(C) 面积(S)
长方形
三角形
梯形
圆
b
a
a
b
c
h
r
一个正方形盒子的棱长为acm,用含a的式子表示:
盒子的表面积S=____________;
盒子的体积V=____________.
做一做
例2 小莉以5km/ h的速度,走了20km的路程,那么她走了多长时间?如用字母v表示速度,用字母s表示路程,那么她走的时间又如何表示呢?
解: 小莉走20km所花的时间为20÷5=4(h).
若用字母v 表示速度,用字母s 表示路程, 则时间 t = s ÷ v = .
从上述例子看到,用字母表示数,可以统一、简明地表示实际问题中的数量关系.
三、用含字母的式子表示数量关系
1.我们现在讨论的数的范围是有理数,即数a可以是正数,也可以是负数或零,所以a不一定表示正数,-a不一定表示负数.
2.同一问题中,同一字母只能表示同一个量,不能用同一字母表示几个不同的量,不同的量要用不同的字母表示.
注意:
买一个篮球需要x元,买一个排球需要y元,买一个足球需要 z 元,用式子表示买 3个篮球、5个排球、2个足球共需要的钱数.
解:买3个篮球、5个排球、2个足球共需要
元.
做一做
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
课堂小结
④小明语文a分,数学b分,那么这两科的平均分为 分.
③一边长为3,这边上的高为h的三角形面积为 .
① n只青蛙 条腿
②同一笼中有鸡a只、兔b只,则共有头 个,脚 只.
1.填空:
课后练习
√
×
√
×
×
×
×
×
×
2.下列代数式中,哪些书写符合要求?
√
3. 如图,有一块长为a,宽为b的长方形铝片,四角各载去一个相同的边长为x的正方形,折起来做成一个没有盖的盒子,则此盒子的容积的表达式应该 ( )
A. V = x2(a-x)(b-x) B. V = x (a-x)(b-x)
C. V = x2(a-2x)(b-2x) D. V = x(a-2x)(b-2x)
解析:由题意可知盒子的底面长为(a-2x),宽为(b-2x),高为x.因此,盒子的容积为V=x(a-2x)(b-2x).故应选D.
D
4.用棋子摆成下列一组图案:
…
( 1 )
( 2 )
( 3 )
① 填写下表:
图案编号 (1) (2) (3) (4) (5) (10) (100)
棋子个数
② 摆第n个图案需要____个棋子.
3
6
9
12
15
30
300
3n
2.2 列代数式
今年暑假,老师从深圳出发,随旅游团到北京旅游.虽然做了充分准备,但是还遇到了许多数学难题.希望大家能帮帮老师!
情景引入
深圳的气温为 x 摄氏度,北京的气温比深圳低4摄氏度,北京的气温为 摄氏度.
游程1:准备
深圳到北京的距离是s千米,高铁的速度为300千米/小时,到达北京需 小时.
游程2:出发
售票处
……
门票价格
成人:每人60元 学生:每人20元
我们有a个成人, b个学生,买门票需付 ________ 元钱.
游程3:买票
太和殿占地呈长方形,长m米,宽n米太和殿占地面积有多少平方米呢
平方米
游程4:参观
珍宝馆陈列厅呈正方形,边长为a米.地面积有多少平方米呢
平方米
游程4:参观
珍宝馆内有一金嵌珍珠宝石塔,宝石塔外边是一个长方体的玻璃罩,它的长、宽、高分别是3、p、q米.此玻璃罩的体积为多少?
立方米
游程4:参观
像 的式子都是用运算符号把数与字母连接而成的,叫做代数式.
一、代数式的概念
概念学习
(运算符号包括+、-、×、÷、乘方)
判断下列式子哪些是代数式,哪些不是.
(3) x=2 (4)13
( √ )
( √ )
( × )
( × )
( √ )
(5) (6) x+2>3
(1) a2+b2 (2)
( × )
练一练
注意:(1)代数式中不含表示关系的符号
(“=”“>”“<”“≥”“≤”“≠”).
(2)单独的一个数或字母也是代数式.
例1 用代数式表示:
(1)a的7倍与2b的差;
(2)x,y两数的平方和减去两数积的2倍;
(3)a的倒数与b的和.
解:
(1) ;
(2) ;
(3) .
典例精析
(1)已知铅笔每支x元,练习本每本y元.小明买铅笔5支,练习本6本,需多少元?
二、列代数式
例2 列代数式:
(5x+6y)元;
(2)小兰家距学校5km.她步行的速度是vkm/h,而骑自行车比步行快10km/h.她骑自行车的速度是多少?她骑自行车从家到学校需多长时间?
小兰骑自行车的速度是(v+10)km/h,从家到学校需
列代数式就是把实际问题中与数量有关的语句,用含有数、字母和运算符号的式子表示出来,也就是把文字语言转化为符号语言.
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
方法归纳
(1)一条河的水流速度是2.5 km/h,船在静水中的速度是 v km/h,用式子表示船在这条河中顺水行驶和逆水行驶时的速度.
例3
分析:顺水行驶时,船的速度=船在静水中的速度+水流速度;
逆水行驶时,船的速度=船在静水中的速度-水流速度.
解:(1)船在这条河中顺水行驶的速度是 km/h,逆水行驶的速度是 km/h.
(2)如左下图(图中长度单位:cm),用式子表示三角尺的面积;
(3)右 下图是一所住宅的建筑平面图(图中长度单位:m),用式子表示这所住宅的建筑面积.
解:(2)三角尺的面积是( )cm2.
(3)这所住宅的建筑面积是( )m2.
列式要点:
①要抓住关键词语,明确它们的意义以及它们之间的关系,如和、差、积、商及大、小、多、少、倍、分、倒数、相反数等;
②理清语句层次明确运算顺序;
③牢记一些概念和公式.
方法归纳
(1)某种商品每袋4.8元,在一个月内的销售量是m 袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是 r,h,用式子表示圆柱体的体积.
练一练
(3)有两片棉田,一片有m hm2 (公顷,1 hm2 =104 m2 ),平均每公顷产棉花a kg;另一片有n hm2 ,平均每公顷产棉花b kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a mm,小正方形的边长是b mm,用式子表示剩余部分的面积.
代数式10x+5y可以表示什么?
如果用x表示1支铅笔的价格,用y表示1本练习本的价格,那么10x+5y可以表示_______________________的总钱数;
想一想:
10支铅笔与5本练习本
三、解释代数式所表示的实际意义
例4 下列代数式可以表示什么?
(1)2a-b;(2)2(a-b).
解:(1)若篮球的单价是a元,足球的单价是b元,2a-b可表示为卖两个篮球比买一个足球多花(2a-b)元;
(2)若某商店的一台学习机的售价为a元,进价为b元,2(a-b)可表示为卖出两台学习机给商店盈利2(a-b)元.
代数式
根据实际问题列代数式
代数式的概念
解释解释代数式所表示的实际意义
判别代数式
代数式的书写要求
课堂小结
(1)5箱苹果重m kg,每箱重 kg ;
(2)一个数比a的2倍小15,则这个数为 ;
(3)全校学生总数是x,其中女生占总数52%,则女生人数是 ,男生人数是 ;
(4)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共有
本;
1.用式子表示下列数量:
课后练习
2.判断下列式子哪些是代数式,哪些不是
(5)3×(4 -5) (6) 3×4 -5 =7
(7)x-1≤0 (8) x+2>3
(9)10x+5y=15 (10) +c
(1)a2+b2 (2)
(3)13 (4)x=2
(1)(2)(3)(5)(10)是代数式;
(4)(6)(7)(8)(9)不是代数式.
3.说出下列代数式的意义:
(1)圆珠笔每支售价a元,练习簿每本售价b元,那么,3a+4b表示什么?
(2)长方形的长、宽分别为a、b,那么a(b+1)表示什么?
解:(1) 3支圆珠笔与4本练习簿的总价格;
(2)长为a,宽为b+1的长方形的面积.
2.3 代数式的值
据报纸记载,一位医生研究得出由父母身高预测子女成年后身高的公式:儿子身高是由父母身高的和的一半,再乘以1.08;女儿的身高是父亲身高的0.923倍加上母亲身高的和再除以2.
情景引入
(1)已知父亲身高是a米,母亲身高是b米,试用代数式表示儿子和女儿的身高;
(2)五年级女生小红的父亲身高是1.75米,母亲的身高是1.62米;六年级男生小明的父亲的身高是1.70,母亲的身高是1.62,试预测成年以后小明与小红谁个子高?
一、求代数式的值
合作探究
数值转换机
输入 -2 -1/2 0 0.26 1/3 5/2 4.5
机器1的输出结果
机器2的输出结果
输入x
输入x
输出
输出
×6
-3
-15
-6
-3
-1.44
-1
12
24
-30
-21
-18
-16.44
-16
-3
9
×6
-3
议一议
n 1 2 3 4 5 6 7 8
5n+6
n2
11
(1)随着n的值逐渐变大,两个代数式的值如何变化?
(2)估计一下,哪个代数式的值先超过100.
16
21
26
31
36
41
46
1
4
9
16
25
36
49
64
逐渐增大
n2 先超过
填写下表,并观察下列两个代数式的值的变化情况.
例1 (1)当x=-3时,求 的值;
(2)当a=0.5,b=-2时,求 的值.
解:(1)当x=-3时,
(2)当a=0.5,b=-2时,
典例精析
针对训练
1.当x=-3,y=2时,求下列代数式的值:
解:
当x=-3,y=2时,
2.
解:
方法归纳
1.求代数式的值的步骤:
(1)写出条件:当……时
(2)抄写代数式
(3)代入数值
(4)计算
解:当x=2,y=-3时,
x(x-y)
= 2×[2-(-3)]
=2 ×5
=10
当x=2,y=-3时,求代数式x(x-y)的值.
(1)代入时,要“对号入座”,避免代错字母,其他符号不变.
(2)代数式中,代入数值以后原来省略的乘号一定要还原.
(3)若字母的值是负数或分数,将字母的值代入代数式时,应加上括号,原来的数字和运算符号都不能改变.
2.在代入数值时应注意:
例2 已知x-2y=3,则代数式6-2x+4y的值.
解:6-2x+4y=6-2(x-2y),
因为x-2y=3,将其代入上式中,可得
6-2x+4y=6-2×3=0.
相同的代数式可以看作一个字母——整体代入
典例精析
【变式】已知 则 的值是多少?
解:
由
可得
将
代入上式:
练一练
当x=1时,代数式 ,当x=-1时,该代数式的值是多少?
解:将x=1代入代数式,得a+b=2018,当x=-1时,
二、间接(或根据公式)求代数式的值
例3 我们在计算不规则图形的面积时,有时采用“方格法”来计算.计算方法如下:假定每个小方格的边长为1个单位长,S为图形的面积,L是边界上的格点数,N是内部格点数,则有 . 请根据此方法计算图中四边
形ABCD的面积.
解:由图可知边界上的格点数L=8,
内部格点数N =12,
所以四边形ABCD的面积为
例4 堤坝的横截面是梯形,测得梯形上底为a=18m,下底b=36m,高h=20m,求这个截面的面积.
a
b
h
解:梯形面积公式为:
将a=18m,b=36m,h=20m代入上面公式,得
答:堤坝的横截面积是
a
b
h
代数式的值
概念
应用
用数字代替代数式中的 ,
按照代数式中的 关系计算得出的结果叫做代数式的值.
运算
字母
直接代入求值
列代数式求值
整体代入求值
步骤
1.代入
2.计算
课堂小结
1.当a=2,b=1,c=3时代数式c-(c-a)(c-b)的值是( )
5.已知a+b=3 , 则4–a-b=______.
A.1 B.2 C.3 D.4
A
2.如果2a+3b=5,那么4a+6b-7=__.
3
3.已知a+b=5,ab=6 ,则ab-(a+b)=___.
4. 当a=-2,b=-1时,1-|b-a|=_____.
6.已知2x2+3x+7=8 , 则4x2+6x-9=______.
1
1
0
-7
课后练习
7.某公园的门票价格是:成人10元/张;学生5元/张.
(1)一个旅游团有成人x人、学生y人,那么该旅游团应付多少门票费?
(2)如果该旅游团有37个成人、15个学生,那么他们应付多少门票费?
解:(1)该旅游团应付的门票费是(10x+5y)元.
(2)把x=37,y=15代入代数式,得
10x+5y =10×37+5×15 =445.
因此,他们应付445元门票费.
8.现代营养学家用身体质量指数衡量人体胖瘦程度,这个指数等于人体质量(千克)与人体身高(米)平方的商.对于成年人来说,身体质量指数在20~25之间,体重适中;身体质量指数低于18,体重过轻;身体质量指数高于30,体重超重.
(1)设一个人的体重为w(千克),身高为h(米),求他的身体质量指数.
解:他的身体质量指数为
(2)张老师的身高是1.75米,体重是65千克,他的体重是否适中?
解:(2)把w=65,h=1.75代入代数式,得
由于21在20到25之间,因此,他的体重适中.
2.4 整 式
这两个式子都是代数式,那么不同的代数式之间又有哪些区别和联系呢?
某学校的操场如图所示,由一个长方形和两个半圆组成.
(2)整个操场的面积是多少?
(1)两个半圆的面积是多少?
情景引入
一、单项式的相关概念
用含有字母的式子填空
1. 棱长为a的正方形的表面积为____ ;体积为_ __.
3. 一辆汽车的速度是vkm/h,它t小时的行驶路程为 km.
2. 铅笔的单价为x元,圆珠笔的单价是铅笔的单价2.5倍,圆珠笔的单价是 元.
vt
2.5x
6a2
a3
4. 一个圆的半径是r cm,它周长是 cm.
2πr
思考: 6a2,a3,2.5x,vt,2πr 以上各式中运算
有什么共同特点?
上面各式的运算中数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示字母与数字、字母与字母的积).
这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
例如:像-2,a,-b, 等是单项式.
注意:像 , , 等不是单项式.
为什么?
概念学习
练一练
下列式子中哪些是单项式
√
√
√
√
√
√
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法:
方法总结
思考:单项式中的数字和字母各有何意义呢
a
2
6
系数
次数
__
1
5
=-
ab
系数
定义:单项式中数与字母相乘,通常把数字因数
叫做系数;所有字母的指数的和叫做这个
单项式的次数.
二次
次数
典例精析
练一练
1.判断下列说法是否正确:
①-7xy2的系数是7;( )
②-x2y3与x3没有系数;( )
③-ab3c2的次数是0+3+2;( )
④-a3的系数是-1; ( )
⑤-32x2y3的次数是7;( )
⑥ πr2h的系数是 .( )
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
(1)每包书有12册,n包书有_____册;
(2) 底边长为a,高为h的三角形的面积是_____;
(3) 一个长方体的长和宽都是a,高为h,它的体积是_____;
(4)一台电视机原价为a元,现按原价的九折出售,这台电视机现在的售价为____;
(5)一个长方形的长为0.9,宽为a,面积是____.
1
2.用单项式填空,并指出它们的系数和次数:
12n
0.9a
0.9a
一次
二次
三次
一次
一次
1.单项式的系数:单项式中的数字因数.若一个单项式只含有字母因数,那么它的系数就是1或-1;若单项式是单独一个数,则系数就是它本身.
2.单项式的次数应是该单项式中所有字母的指数和,与系数的指数没关系,如24x2y3的次数是5,而不是9;单独一个数的次数是0.
3.不要把π当成字母.
归纳总结
二、多项式及其有关概念
(1)若三角形的三条边长分别为a、b、c,则三角形的周长是________;
(2)某班有男生x人,女生21人,这个班的学生一共有
_____人;
(3)如图,三角尺的面积为 .
a+b+c
(x+21)
列代数式:
它们是单项式吗?这些式子有什么共同特点?与单项式有什么关系?
议一议
单项式
单项式
+
上述几个式子都是两个或者多个单项式相加的形式.
a+b+c
(x+21)
多项式有关概念
1.几个单项式的和叫做多项式.
2.在多项式中,每个单项式叫做多项式的项.
3.不含字母的项叫做常数项.
4.多项式里次数最高项的次数就是多项式的次数.
单项式与多项式统称为整式.
多项式:
常数项
次数
概念学习
例2 说出下列多项式的次数和常数项:
解:
(1)
(2)
(3)
(1) 的次数是1,常数项是-3.
(2) 的次数是3,常数项是-4;
(3) 的次数是2,常数项是-9.
例3 下列整式中哪些是单项式?哪些是多项式?是
单项式的指出系数和次数,是多项式的指出项和次数:
x
32t3
1
32
1
3
0
6
3
解:
1
4
2
要点归纳:
(1)多项式的各项应包括它前面的符号
(3)要确定一个多项式的次数,先要确定此多项式中各项(单项式)的次数,然后找次数最高的
(4)一个多项式的最高次项可以不唯一
(2)多项式没有系数的概念,但其每一项均有系数,每一项的系数也包括前面的符号
例4 已知-5xm+104xm+1-4xmy2是关于x、y的六次多项式,求m的值,并写出该多项式.
解:由题意得m+2=6,所以m=4.
归纳总结:解题的关键是弄清多项式次数是多项式中次数最高的项的次数.然后根据题意,列出方程,求出m的值.
分析:该多项式最高次项为-4xmy2,其次数为m+2,故m+2=6.
所以该多项式为-5x4+104x5-4x4y2.
【变式】若关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,求m、n的值.
解:∵关于x的多项式-5x3-mx2+(n-1)x-1不含二次项和一次项,
∴m=0,n-1=0,
则m=0,n=1.
做一做
1.多项式x2+y-z是单项式___,___,___的
和,它是___次___项式.
2.多项式3m3-2m-5+m2的常数项是____,二次
项是_____,二次项的系数是_____.
x2
y
-z
二
三
-5
m2
1
二、多项式的应用
例5 如图所示,用式子表示圆环的面积.当 cm,
cm时,求圆环的面积( 取 ).
解:外圆的面积减去内圆的面积就是圆环
的面积,所以圆环的面积是 .
这个圆环的面积是
cm2 .
当 cm , cm 时,
圆环的面积是
做一做
(2) , 分别表示梯形的上底和下底, 表示
梯形的高,则梯形面积 = ,当
=2 cm, =4 cm, =5 cm时, = cm 2 .
1.(1) , 分别表示长方形的长和宽,则长方形的周长
= ,面积 = ,当 =2 cm,
=3 cm时, = cm, = cm 2 ;
2.小红和小兰房间窗户的装饰物如图所示,它们分别由两个四分之一圆和四个半圆组成(半径分别相同).
(1)窗户中能射进阳光的部分的面积分别是多少?
a
b
a
b
(2)你能指出其中的单项式或多项式吗?它们的次数分别是多少?
都是多项式,次数都是2次
整式
单项式
多项式
由数与字母的积组成的代数式叫单项式
单独一个字母或一个数也是单项式
单项式中,与字母相乘的数叫做单项式的系数
单项式中所有字母的指数的和叫做这个单项式的次数
由几个单项式的和组成的代数式叫做多项式
不含字母的项叫做常数项
多项式中次数最高的项的次数叫做这个多项式的次数
组成多项式的每个单项式叫做多项式的项
课堂小结
1.下列式子中,哪些是单项式?哪些是多项式?哪些是整式?
3x,2x-1, ,-ab,-5, -1,3m-4n+m2n.
课后练习
2.判断正误:
(1)多项式-x2y+2x2-y的次数2.( )
(2)多项式 - -a+3a2的一次项系数是1.( )
(3)-x-y-z是三次三项式.( )
3.一个关于字母x的二次三项式的二次项系数为4,一次项系数为1,常数项为7,则这个二次三项式为___.
×
×
×
4x2+x+7
4.如图,某居民小区有一块宽为2a米,长为b米的长方形空地,为了美化环境,准备在此空地的四个顶点处各修建一个半径为a米的扇形花台,在花台内种花,其余种草.如果建造花台及种花费用每平方米为100元,种草费用每平方米为50元.那么美化这块空地共需多少元?
解:花台面积和为πa2平方米,
草地面积为(2ab-πa2)平方米.
所以需资金为[100πa2+50(2ab-πa2)]元.
2.5 整式的加法和减法
第1课时 合并同类项
生活中,我们常常把具有相同特征的事物归为一类 ,请同学们给下列物品分类.
蔬菜
水果
情景引入
观察超市货物摆放
观察药店药品摆放
如果有一罐硬币(分别为一角、五角、一元的),你会如何去数呢
储蓄罐
一、同类项的辨别
-7a2b
问题1 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的次数的特征将这些小白兔分到三个不同的栅栏里吗?
8n
3ab2
2a2b
6xy
5n
-3xy
-ab2
-7a2b
问题2 有八只小白兔,每只身上都标有一个单项式,你能根据这些单项式的特征将这些小白兔分到四个不同的栅栏里吗?这些被归为同一类的兔子有什么相同的特征?
8n
3ab2
2a2b
6xy
5n
-3xy
-ab2
同类项:所含字母相同,并且相同字母的指数也分别相等的项叫做同类项.
(1)两个相同:字母相同;相同字母的次数相同;
(2)两个无关:与系数大小无关;与字母顺序无关;
(3)所有的常数项都是同类项.
说明:
知识要点
游戏一
游戏二
(3)-3pq与3qp
(1)2x2y与-3x2y
(2)2abc与2ab
(4) -4x2y与5xy2
先判断每一组是否是同类项,若不是的,请为前者配一个.
√
√
3abc
x2y
×
×
总结归纳
(1)同类项只与字母及其指数有关,与系数无关,与字母在单项式中的排列顺序无关;
(2)抓住“两个相同”:一是所含的字母要完全相同,二是相同字母的指数要相同,这两个条件缺一不可.
同类项的判别方法
(3)不要忘记几个单独的数也是同类项.
典例精析
例1 (1)如果2a2bn+1与-4amb3是同类项,则m= ,n= .
(2)在6xy-3x2-4x2y-5yx2+x2中没有同类项的项是 .
2
2
6xy
分析:(1)根据同类项的定义,可知a的指数相同,b的指数也相同,即m=2,n+1=3.
二、合并同类项
x
x
x
2
+ 3
=
5
=
3
-
a2bc
a2bc
a2bc
2
奇妙的替换
你还有其他方法解释吗?
利用乘法分配律可得
(2+3)
x
x
2
+ 3
=
x
=
3
a2bc
a2bc
a2bc
-2
(3-2)
= 5x
= a2bc
把同类项合并成一项叫做合并同类项.
解:
(1)
(2)
例2. 合并下式中的同类项:
(1) (2)
解:
(1)
(1)
1.将同类项在底下划线标出;
2.运用加法的交换律和结合律,把同类项放在一起;
3.合并同类项.
注意:对于不同的同类项,分别用不同的线标出.
例3. 合并下式中的同类项:
(1)
(2)
“合并同类项”的方法:
一找,找出多项式中的同类项,不同类的同类项用不同的标记标出;
二移,利用加法的交换律,将不同类的同类项集中到不同的括号内;
三合,将同一括号内的同类项相加即可.
总结归纳
系数相加,字母及其指数不变
(1)a+a=2a
(2)3a+2b=5ab
(3)5y2-3y2=2
下列合并同类项对吗?不对的,说明理由.
(4)4x2y-5xy2=-x2y
(5)3x2+2x3=5x5
(6)a+a-5a=-3a
说一说
×
√
×
×
×
√
你会计算吗?
⑴ 100t-252t ;
⑵ 3a+2b-5a-b ;
⑶ -4ab+8-2b2-9ab-8 .
试一试
答案:⑴-152t ; ⑵-2a+b ; ⑶-13ab-2b2.
先分组,再合并
练一练
合并同类项:
(1)6x+2x2-3x+x2+1;
(2)-3ab+7-2a2-9ab-3.
解:(1)原式=(6x-3x)+(2x2+x2)+1
=3x+3x2+1
(2)原式=(-3ab-9ab)-2a2+(7-3)
=-12ab-2a2+4
例4 (1)求多项式 的值,
其中x = ;
(2)求多项式 的值,
其中a= ,b=2,c=-3.
分析:在多项式求值时,可以先将多项式中的同类项合并,然后再代入求值,这样可以简化计算.
解:(1)
当x = 时,原式=
(2)
当a= ,b=2,c=-3时,原式=1.
议一议
在不知道a,b的情况下,能否求出“7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2”的值,若能,请求出数值;若不能,请说明理由.
解:能.理由如下:
化简7a2-5b2+3a2b-4a2+b2-3a2b-3a2+4b2-2
=(7a2-4a2-3a2)+(-5b2+b2+4b2)+(3a2b-3a2b)-2
=-2,
所以无论a,b取任何值,代数式的值都为2.
例5 一天,王村的小明奶奶提着一篮子土豆去换苹果,双方商定的结果是:1千克土豆换0.5千克苹果.当称完带篮子的土豆重量后,摊主对小明奶奶说:“别称篮子的重量了,称苹果时也带篮子称,这样既省事又互不吃亏.”你认为摊主的话有道理吗?请你用所学的有关数学知识加以判定.
解:设土豆重a千克,篮子重b千克,则应换苹果0.5a千克.若不称篮子,则实换苹果为0.5a+0.5b-b=(0.5a-0.5b)千克,很明显小明奶奶少得苹果0.5b千克.所以摊主说得没有道理,这样做小明奶奶吃亏了.
合并同类项的方法——“一加二不变”
同类项的概念
与系数无关
与所含字母的顺序无关
两无关
两同
相同字母的指数相同
所含字母相同
合并同类项
课堂小结
一、填空题.
1.如果5x2y与xmyn是同类项,那么 m=____,n=____.
2.合并同类项:
(1)-a-a-2a=________.
(2)-xy-5xy+6yx=________.
(3)0.8ab2-a2b+0.2ab2=_______.
2 1
-4a
0
ab2-a2b
课后练习
二、选择题.
3.下列各组式子中是同类项的是( )
A.-2a与a2 B.2a2b与3ab2
C.5ab2c与-b2ac D.-ab2和4ab2c
4.下列运算中正确的是( )
A.3a2-2a2=a2 B.3a2-2a2=1
C.3x2-x2=3 D.3x2-x=2x
C
A
课后练习
三、合并下列各式中的同类项:
5.-7mn+mn+5nm;
6.3a2b-4ab2-4+5a2b+2ab2+7.
四、求下列各式的值:
7.3x2-8x+2x3-13x2+2x-2x3+3,其中x=-1.
8.a2b-6ab-3a2b+5ab+2a2b,其中a=0.1,b=0.01.
-mn
8a2b-2ab2+3
-10
1
2
-0.001
2.5 整式的加法和减法
第2课时 去括号
同学们还记得用火柴棒搭正方形时,怎样计算所需要的火柴棒的根数吗?拿出准备好的火柴自己搭一下,然后再按如下做法搭.
第一个正方形用4根,每增加一个正方形增加3根,那么搭x个正方形就需要火柴棒
根.
[4+3(x-1)]
情景引入
把每一个正方形都看成是用4根火柴棒搭成的,然后再减多算的根数,得到的代数式是 .
[4x-(x-1)]
(3x+1)
一、去括号法则
合作探究
搭x个正方形,用的方法不一样,列出的式子不同,但所用火柴棒的根数一样,用数学知识来说明它们为什么相等呢?
代数式4+3(x-1),有括号,用乘法分配律可以把3乘到括号里,得4+3x-3,而4与-3是同类项可以合并,这时,代数式就变为3x+1.
即4+3(x-1)
=4+3x-3 (乘法分配律)
=3x+1. (合并同类项)
代数式4x-(x-1)可以看作是4x+[-(x-1)],而-(x-1)可写成(-1)(x-1),所以4x-(x-1)就等于4x-x+1,合并同类项得3x+1.
从而得出结论:这三个代数式是相等的.
即4x-(x-1)
=4x+(-1)(x-1)
=4x-x+1
=3x+1.
议一议
观察比较两式等号两边画横线的变化情况.
(1)4+ 3(x-1) =4+ 3x-3 =3x+1;
(2)4x -(x-1) =4x -x+1 =3x+1.
去括号前后,括号里各项的符号有什么变化?
思考:
括号前是“+”号,把括号和它前面的“+”号去掉后,原括号里各项的符号都不改变;
括号前是“-”号,把括号和它前面的“-”号去掉后,原括号里各项的符号都要改变.
去括号法则:
例1 计算:
(1) (5x-1)+(x-1) ; (2) (2x+1)-(4-2x).
解:
(1) (5x-1)+(x-1)
=5x-1+x-1
=6x-2;
(2) (2x+1)-(4-2x)
=2x+1-4+2x
=4x-3.
括号前是“+”号,运用加法结合律把括号去掉,括号里各项的符号都不改变.
括号前是“-”号,把括号和它前面的“-”号去掉,原括号里各项都符号都要改变.
典例精析
【归纳总结】
(1)去括号时,不仅要去掉括号,还要连同括号前面的符号一起去掉.
(2)去括号时,首先要弄清括号前是“+”号还是“-”号.
(3)注意法则中的“都”字,变号时,各项都变号;不变号时,各项都不变号.
(4)当括号前有数字因数时,应运用乘法分配律运算,切勿漏乘.
(5)出现多层括号时,一般是由里向外逐层去括号.
判断正误
(1)3(x+8)=3x+8
(2)-3(x-8)=-3x-24
(4)-2(6-x)=-12+2x
(3)4(-3-2x)=-12+8x
错
3x+3×8
错因:分配律,漏乘3.
错
-3x+24
错因:括号前面是负数,去掉负号和括号后每一项都变号.
对
错
错因:括号前面是正数,去掉正号和括号后每一项都不变号.
-12-8x
做一做
二、利用去括号化简求值
练一练
先化简,再求值:3x2+(2x2-3x)-(-x+5x2),其中x=314.
解:原式=3x2+2x2-3x+x-5x2=-2x.
当x=314时,原式=-2×314=-628.
例3 两船从同一港口出发反向而行,甲船顺水,乙船逆水,两船在静水中速度都是50千米/时,水流速度是a千米/时.
问: (1)2小时后两船相距多远
(2)2小时后甲船比乙船多航行多少千米
三、去括号化简的应用
解:顺水速度=船速+水速=(50+a)km/h,
逆水速度=船速-水速=(50-a)km/h.
(1)2小时后两船相距(单位:km)
2(50+a)+2(50-a)=100+2a+100-2a=200.
(2)2小时后甲船比乙船多航行(单位:km)
2(50+a)-2(50-a)=100+2a-100+2a=4a.
括号前面是“+”号,里面各项不变号.
括号前面是“-”号,里面各项全变号.
乘系数
去括号
合并同类项
④代入求值
去括号法则
解题步骤
去括号
课堂小结
1.化简m-n-(m+n)的结果是( )
A.0 B.2m C.-2n D.2m-2n
2.化简4x-4-(4x-5)=________.
3.化简2(2x-5)-3(1-4x)=________.
4.三角形的第一边长是(2a+b)cm,第二边长是2(a+b)cm,第三边长比第二边长短b cm,则这个三角形的周长是________cm.
C
1
16x-13
(6a+4b)
课后练习
5.化简下列各式:
(1)8m+2n+(5m-n); (2)(5p-3q)-3( ).
解:
6.已知2xmy2与-3xyn是同类项,计算m-(m2n+3m-4n)+(2nm2-3n)的值.
答案:2
7.有理数a,b,c在数轴上位置如图,化简代数式│a│-│a+b│+│c-a│+│b-c│
答案:a-2c
8.某商店有一种商品每件成本a元,原来按成本增加b元定出售价,售出40件后,由于库存积压,调整为按售价的80%出售,又销售了60件.
(1)销售100件这种商品的总售价为多少元?
(2)销售100件这种商品共盈利多少元?
解:(1)根据题意得:40(a+b)+60(a+b)×80%=88a+88b(元),
则销售100件这种商品的总售价为(88a+88b)元;
(2)根据题意得:88a+88b-100a=-12a+88b(元),
则销售100件这种商品共盈利(-12a+88b)元.
2.5 整式的加法和减法
第3课时 整式的加减
任意写一个两位数
交换它的十位数字与个位数字,又得到一个数
两个数相加
小组游戏
重复几次看看,谁能先发现这些和有什么规律?对于任意一个两位数都成立吗?
10a+b+10b+a=11a+11b=11(a+b)
一、整式的加减
合作探究
如果用a,b分别表示一个两位数的十位数字和个位数字,那么这个两位数可以表示为: .交换这个两位数的十位数字和个位数字,得到的数是: .将这两个数相加:
+ =
.
10a+b
10b+a
(10a+b)
(10b+a)
结论:
这些和都是11的倍数.
做一做
任意写一个三位数
交换它的百位数字与个位数字,又得到一个数
两个数相减
你又发现什么了规律?
原三位数728,百位与个位交换后的数为827,由728 -827= -99.你能看出什么规律并验证它吗?
设原三位数为100a+10b+c,百位与个位交换后的数为100c+10b+a,它们的差为:
(100a+10b+c)-( 100c+10b+a)
= 100a+10b+c-100c-10b-a
=99a-99c
=99(a-c)
举例:
任意一个三位数可以表示成100a+10b+c
议一议
在上面的两个问题中,分别涉及了整式的什么运算?说说你是如何运算的?
去括号、合并同类项
八字诀
整式的加减运算
解:
有括号要先去括号
有同类项再合并同类项
结果中不能再有同类项
典例精析
例1 求整式 与 的和.
解:根据题意,得
去括号
合并同类项
去括号
合并同类项
例2 求多项式 与多项式 的和与差.
练一练
二、整式加减的应用
解:
当x=1,y=-2时,
例3 先化简,再求值.
,其中x=1,y=-2.
(1)整式的加减运算重点注意去括号时的符号、系数的处理,不要把符号弄错,不要漏乘括号外的系数;
(2)整式的化简求值题,能够化简的最好先化简,尽量不要直接把字母的值代入计算.
方法归纳
的值,
其中
先将式子化简,再代入数值进行计算
解:
当 时,
原式
→去括号
→合并同类项
﹜
将式子化简
练一练
例4 如图,正方形的边长为x,用整式表示图中阴影部分的面积,并计算当x=4m时阴影部分的面积( 取3.14).
x
x
解:阴影部分的面积为:
当x=4m 时,阴影部分的面积为:
解决整式加减的实际应用题时,先要把具体量用代数式表示出来,然后根据整式加减运算的法则、步骤进行计算.
注意最后结果是几个单项式的和的形式,且要带单位时,要整体加括号.
方法归纳
例5 做大小两个长方体纸盒,尺寸如下(单位:cm):
(1)做这两个纸盒共用料多少平方厘米?
长 宽 高
小纸盒 a b c
大纸盒 1.5a 2b 2c
解:小纸盒的表面积是( )cm
2
大纸盒的表面积是( )cm
2
(1)做这两个纸盒共用料
(2ab+2bc+2ca)+(6ab+8bc+6ca)
=2ab+2bc+2ca+6ab+8bc+6ca
=8ab+10bc+8ca(cm )
2
a
b
c
1.5a
2b
2c
2ab
+2bc
+2ca
6ab
+ 8bc
+ 6ca
(2)做大纸盒比做小纸盒多用料
(6ab+8bc+6ca)- (2ab+2bc+2ca)
=6ab+8bc+6ca- 2ab-2bc-2ca
=4ab+6bc+4ca(cm )
2
(2)做大纸盒比小纸盒多用料多少平方厘米?
小纸盒的表面积是(2ab+2bc+2ca)cm
大纸盒的表面积是(6ab+8bc+6ca)cm
2
2
通过上面的学习,你能得到整式加减的运算法则吗?
一般地,几个整式相加减,如果有括号就先去括号,然后再合并同类项.
想一想
例6 已知A=-6x2+4x,B=-x2-3x,C=5x2-7x+1,小明和小白在计算时对x分别取了不同的数值,并进行了多次计算,但所得A-B+C的结果却是一样的.你认为这可能吗?说明你的理由.
理由:A-B+C
=(-6x2+4x)-(-x2-3x)+(5x2-7x+1)
=-6x2+4x+x2+3x+5x2-7x+1
=1.
解:可能.
由于结果中不含x,所以不论x取何值,A-B+C的值都是1.
整式加减的步骤
整式加减的应用
整式的加减
去括号
合并同类项
课堂小结
8a
2x3-xy2
解:(3x2-2x+1)-2(x2-x)-x2=3x2-2x+1-2x2+2x-x2=1
3.计算(3x2-2x+1)-2(x2-x)-x2的值,其中x=-2,小明把“x=-2”错抄成“x=2”,但他的计算结果仍是正确的,这是怎么回事?说明理由.
由于结果中不含x,所以不论x取何值,原式的值都是1.
课后练习
4. 计算
(1)- ab3+2a3b- a2b-ab3- a2b-a3b
(2)(7m2-4mn-n2)-(2m2-mn+2n2)
(3)-3(3x+2y)-0.3(6y-5x)
(4)( a3-2a-6)- ( a3-4a-7)
答案:(1)
5. 一种笔记本的单价是x元,圆珠笔的单价是y元.
小红买这种笔记本3本,买圆珠笔2支;小明买这种
笔记本4本,买圆珠笔3支.买这些笔记本和圆珠笔,
小红和小明一共花费多少钱?
解:小红买笔记本和圆珠笔共花费(3x+2y)元,小明买笔记本和圆珠笔共花费(4x+3y)元.
小红和小明一共花费(单位:元)
(3x+2y)+(4x+3y)
=3x+2y+4x+3y
=7x+5y
你还能有其他解法吗?
另解:小红和小明买笔记本共花费(3x+4x)元,买圆珠笔共花费(2y+3y)元.
小红和小明一共花费(单位:元)
(3x+4x)+(2y+3y)
=7x+5y
分别计算笔记本和圆珠的花费.
6.某公司计划砌一个形状如下图(1)的喷水池,后有人建议改为如下图(2)的形状,且外圆直径不变,只是担心原来备好的材料不够,请你比较两种方案,哪一种需用的材料多(即比较两个图形的周长)?若将三个小圆改为n个小圆,又会得到什么结论?
思路点拨
设大圆半径为R,小圆半径依次为r1,r2,r3,
则图(1)的周长为4πR,图(2)的周长为
2πR+2πr1+2πr2+2πr3=2πR+2π(r1+r2+r3),
因为2r1+2r2+2r3=2R,所以r1+r2+r3=R,因此图(2)
的周长为2πR+2πR=4πR.
这两种方案,用材料一样多,将三个小圆改为n个
小圆,用料还是一样多.
R
2r1+2r2+2r3=2R
小结与复习
第2章 代数式
要点梳理
一、整式的有关概念
1.代数式:把数与表示数的字母用运算符号连接而成的式子叫做代数式.单独一个字母或一个数也是代数式.
2.代数式的值:把代数式里的字母用数代入,计算后得出的结果叫做代数式的值.
3.单项式:由数或字母的____组成的代数式叫做单项式,单独的一个字母或一个数也是单项式.
4.单项式的系数:单项式中,与字母相乘的数做单项式的系数.
积
5.单项式的次数:一个单项式中,所有字母的指数的和叫做这个单项式的次数.
6.多项式:由几个单项式的____组成的代数式叫做多项式.
7.多项式的项:组成多项式的每个单项式叫做多项式的项,其中不含字母的项叫做常数项.
8.多项式的次数:多项式中次数最高的项的次数,叫做这个多项式的次数.
9.整式:________________统称整式.
和
单项式与多项式
二、同类项、合并同类项
1.同类项:所含字母________,并且相同字母的指数也分别______的项,乘它们为同类项.
2.合并同类项:把多项式中的同类项合并成一项,叫做合并同类项.
3.合并同类项时,同类项的系数相加,字母和字母的指数不变.
【注意】
(1)同类项不考虑字母的排列顺序,如-7xy与yx是同类项;
(2)只有同类项才能合并,如x2+x3不能合并.
相同
相同
三、去括号的法则:
(1)如果括号前面是“+”号,运用加法的结合律把括号去掉,原括号里各项的符号都不变.
(2)如果括号前面是“-”号,把括号和它前面的“-”号去掉,原括号里各项的符号都要改变.
四、整式加减
一般地,几个整式相加减,如果有括号就先________,然后再_____________.
去括号
合并同类项
例1:在式子3m+n, -2mn, p, , 0中,单项式的个数是( )
A.3 B.4 C.5 D.6
考点讲练
考点一 整式的有关概念
A
√
√
√
【易错警示】单项式的次数和系数、多项式的次数和项是容易混淆的概念,需辨别清楚.
针对训练
1.在式子x-2,0,-a,-3x2y, , 中,单项式共有( )
A.5个 B.4个 C.3个 D.2个
C
√
√
√
2.代数式 的系数是________,次数是________ .
3
考点二 同类项
例2 若3xm+5y2与x3yn的和是单项式,求mn的值.
【分析】 根据同类项的定义,可知x的指数和y的
指数分别相等.
解:m+5=3,得m=-2,n=2.故mn=(-2)2=4.
【方法技巧】根据同类项的概念,相同字母的指数相等.列方程式解此类题的一般方法.
针对训练
3.若5x2 y与x m yn是同类项,则m=( ) ,n=( )
若5x2 y与x m yn的和是单项式,则m=( ) , n=( )
2
1
2
1
只有同类项才能合并成一项
考点三 去括号
例3 已知A=x3+2y3-xy2,B=-y3+x3+2xy2,
求:(1)A+B;(2)2B-2A.
解:(1)A+B=(x3+2y3-xy2)+(-y3+x3+2xy2)
=x3+2y3-xy2-y3+x3+2xy2
=2x3+y3+xy2.
(2)2B-2A=2(-y3+x3+2xy2)-2(x3+2y3-xy2)
=-2y3+2x3+4xy2-2x3-4y3+2xy2
=6xy2-6y3.
方法总结
去括号是应注意:
(1)括号前是“-”号,去括号时括号里的各项要改变符号;
(2)运用乘法分配律时不要漏乘其中的项.
针对训练
4.下列各项中,去括号正确的是( )
A.x2-(2x-y+2)=x2-2x+y+2
B.-(m+n)-mn=-m+n-mn
C.x-(5x-3y)+(2x-y)=-2x+2y
D.ab-(-ab+3)=3
C
考点四 整式的加减运算与求值
例4 已知
求3A+2B-36C的值,其中x=-6.
解:
当x=-6时,-x+24=-(-6)+24=30.
方法总结
在求多项式的值时,一般情况下是先化简,然后再把字母的值代入化简后的式子中求值,化简的过程就是整式运算的过程.
5. 已知式子x2+3x+5的值为7,那么式子3x2+9x-2的值是( )
A.0 B.2 C.4 D.6
针对训练
【解析】已知x2+3x+5=7,目前没办法解出x.可以考虑把x2+3x当做一个整体,于是可得x2+3x=2.
因此3x2+9x-2=3(x2+3x)-2=3×2-2=6-2=4.故选A.
A
运用整体思想
考点五 与整式的加减有关的探索性问题
例5 甲对乙说:“有一个游戏,规则是:任意想一个数,把这个数乘以2,结果加上8,再除以2,最后减去所想的数,此时我就知道结果”请你说说甲为什么会知道结果.
解:设所想的数为n,
则(2n+8)÷2-n=n+4-n=4.
因为结果是常数4,
所以与所想的数无关,因此甲能知道结果.
方法总结
解决此类问题的关键是根据游戏规则正确列出式子,并化简.
针对训练
6. 学习了有理数的运算后,小明设计了一种计算程序,如图所示,当小明输入-6时,则输出值y=________.
36
7. 观察下列图形:它们是按一定规律排列的,依照此规律,第2016个图形中共有________个五角星.
6049
【解析】可以发现每个图形的五角星个数都比前面一个图形的五角星个数多3个.由于第1个图形的五角星个数是3×1+1,所以第n个图形的五角星个数是3n+1,故第2016个图形五角星个数是3×2016+1=6049.
课堂小结
整 式 的 加 减
用字母表示数
单项式:
多项式:
去括号:
同类项:
合并同类项:
整式的加减:
系数、次数
项、次数、常数项
定义、“两相同、两无关”
定义、法则、步骤
法 则
步 骤
整 式
同课章节目录
