名校联盟2022-2023学年高二上学期开学模拟考试——数学试题2(Word版含解析)
文档属性
| 名称 | 名校联盟2022-2023学年高二上学期开学模拟考试——数学试题2(Word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-04 15:13:24 | ||
图片预览


文档简介
名校联盟2022-2023学年高二上学期开学模拟考试——数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小明跟父母 爷爷和奶奶一同参加《中国诗词大会》的现场录制,5人坐一排.则小明的父母都与他相邻的概率为( )
A. B. C. D.
2.甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为和,则两人合作译出密码的概率为( ).
A. B. C. D.
3.已知复数(其中i为虚数单位,)在复平面内对应的点为,则实数a的值为( )
A.1 B.2 C. D.0
4.正方体ABCD-A1B1C1D1中,M、N分别为棱AB,DD1中点,则异面直线A1M与C1N所成的角是( )
A.0 B. C. D.
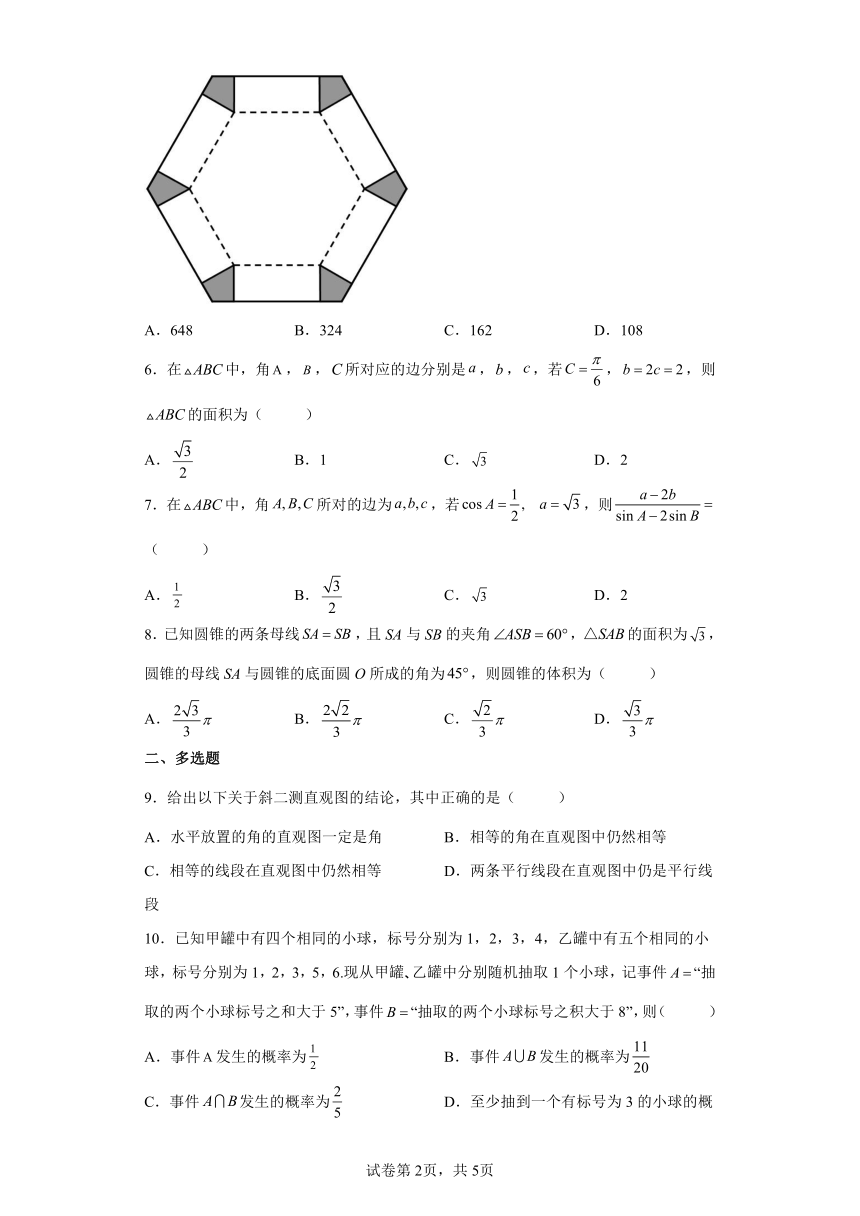
5.河北定州中学数学建模社团开展劳动实习,学习加工制作糖果包装盒.现有一张边长为10的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成底面边长为6的正六棱柱无盖包装盒,则此包装盒的体积为( )
A.648 B.324 C.162 D.108
6.在中,角,,所对应的边分别是,,,若,,则的面积为( )
A. B.1 C. D.2
7.在中,角所对的边为,若,则( )
A. B. C. D.2
8.已知圆锥的两条母线,且SA与SB的夹角,的面积为,圆锥的母线SA与圆锥的底面圆O所成的角为,则圆锥的体积为( )
A. B. C. D.
二、多选题
9.给出以下关于斜二测直观图的结论,其中正确的是( )
A.水平放置的角的直观图一定是角 B.相等的角在直观图中仍然相等
C.相等的线段在直观图中仍然相等 D.两条平行线段在直观图中仍是平行线段
10.已知甲罐中有四个相同的小球,标号分别为1,2,3,4,乙罐中有五个相同的小球,标号分别为1,2,3,5,6.现从甲罐 乙罐中分别随机抽取1个小球,记事件“抽取的两个小球标号之和大于5”,事件“抽取的两个小球标号之积大于8”,则( )
A.事件发生的概率为 B.事件发生的概率为
C.事件发生的概率为 D.至少抽到一个有标号为3的小球的概率为
11.已知正方体的棱长为2,点分别是棱的中点,点在四边形内(包括边界)运动,则下列说法正确的是( )
A.截面的面积是
B.点和点到平面的距离不相等
C.若平面,则点的轨迹的长度是
D.若平面,则点的轨迹的长度是
12.已知正四面体的棱长为,则( ).
A. B.四面体的表面积为
C.四面体的体积为 D.四面体的外接球半径为
三、双空题
13.已知半径为的球面上有、、、四点,满足,,,则球心到平面的距离为___________,三棱锥体积的最大值为___________.
四、填空题
14.设复数,在复平面内的对应点关于虚轴对称,且(为虚数单位),则______.
15.已知为所在平面内一点,且满足,则的面积与的面积之比为_________.
16.已知在中,,,,点P为所在平面内一点,且. 若,则实数_______.
五、解答题
17.甲、乙两人玩一种猜数游戏,每次由甲、乙各出1到4中的一个数,若两个数的和为偶数算甲赢,否则算乙赢.
(1)若事件A表示“两个数的和为5”,求P(A);
(2)现连玩三次,若事件B表示“甲至少赢一次”,事件C表示“乙至少赢两次”,试问B与C是不是互斥事件 为什么
(3)这种游戏规则公平吗 试说明理由.
18.已知,是平面内两个不共线的非零向量,,,,且,,三点共线.
(1)求实数的值;
(2)若,,求的坐标;
(3)已知,在(2)的条件下,若,,,四点按顺时针顺序构成平行四边形,求点的坐标.
19.(1)已知正四棱锥的底面边长是6,侧棱长为5,求该正四棱锥的体积
(2)如图(单位:cm),求下图中阴影部分绕AB旋转一周所形成的几何体的体积.
20.已知复数是实数.
(1)求复数;
(2)若复数是关于的方程的根,求实数和的值.
21.为过接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动,现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)为6组:,,,,,,得到如图所示的频率分布直方图.
(1)求a的值;
(2)记A表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计A的概率;
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成低于90分为“非优秀”,请将下面的列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 非优秀 合计
男生 40
女生 50
合计 100
参考公式及数据:,.
0.10 0.05 0.025 0.01 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
22.如图,平面平面,在矩形中,,四边形为菱形,为线段的中点,.
(1)证明:平面.
(2)求三棱锥的体积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
利用捆绑法求出排列数,进而可得概率.
【详解】
将小明父母与小明三人进行捆绑,其中小明居于中间,形成一个元素,与其他两个元素进行排序,则,
故所求的概率为,
故选:.
2.D
【解析】
【分析】
利用独立事件乘法公式、互斥事件的加法公式求两人合作译出密码的概率即可.
【详解】
由题意,两人合作译出密码的概率.
故选:D
3.A
【解析】
【分析】
先利用复数的乘法化简,再利用复数的几何意义求解.
【详解】
因为,
又因为复数在复平面内对应的点为,
所以,
解得
故选:A
4.D
【解析】
【分析】
取的中点,连接,交于,则可证得∥,则或其补角为异面直线A1M与C1N所成的角,然后由≌,可求出的大小
【详解】
取的中点,连接,交于,
因为N为DD1中点,
所以,∥,
所以四边形为平行四边形,
所以∥,
所以或其补角为异面直线A1M与C1N所成的角,
因为M为AB中点,为的中点,,
所以,
因为,
所以≌,
所以,
因为,
所以,
所以,
所以异面直线A1M与C1N所成的角是,
故选:D
5.B
【解析】
【分析】
利用正六边形的性质求出正六棱柱的高,再根据棱柱的体积:即可求解.
【详解】
如图:由正六边形的每个内角为,
按虚线处折成底面边长为6的正六棱柱,即,
所以 ,即正六棱柱的高为
所以正六棱柱体积:.
故选:B
6.A
【解析】
【分析】
利用正弦定理可出角,进而可得角,再利用三角形面积公式求解即可.
【详解】
在中,由正弦定理,得,即,所以,
又,所以,所以,
所以的面积.
故选: A
7.D
【解析】
【分析】
先求出的值,然后根据正弦定理进行边化角即可求出.
【详解】
因为,所以,
所以由正弦定理,得,所以,
所以.
故选:D.
8.B
【解析】
【分析】
由三角形的面积计算出边长,然后根据圆锥的母线SA与圆锥的底面圆O所成的角为得出高,由圆锥的体积公式即可得出结果.
【详解】
由圆锥的两条母线,,可得三角形的面积为:,.
设圆锥的高为h,底面圆O的半径为R,由圆锥的母线SA与圆锥的底面圆O所成的角为,可得,,,
则圆锥的体积:,
故选:B
9.AD
【解析】
【分析】
根据直观图和斜二测画法的规则,判断选项.
【详解】
水平放置的角的直观图一定是角,故A正确;角的大小在直观图中都会发生改变,有的线段在直观图中也会改变,比如正方形的直方图中,故BC错误;
由斜二测画法规则可知,直观图保持线段的平行性,所以D正确.
故选:AD
10.BCD
【解析】
【分析】
根据题意分别列出事件A和事件B所包含的基本事件,再逐个选项判定,即可求解.
【详解】
由题意知,从甲罐,乙罐中分别随机抽取1个小球,共有个基本事件,
其中事件A包含的基本事件有:
,共有11个基本事件;
事件B包含的基本事件有:,共有8个基本事件,
对于A中事件A发生的概率为,所以A不正确;
对于B中,由以上可得事件B是事件A的子事件,所以事件的概率为,
所以B正确;
对于C中,由事件B是事件A的子事件,所以事件概率为,所以C正确;
对于D中,可分为三种情况:当甲罐中抽到3,乙罐不是3时,有种;当甲罐不是3,乙罐是3时,有;当甲罐抽到3且乙罐也是3时,有1种,所以至少抽到一个有标号为3的小球的概率为,所以D正确.
故选:BCD.
11.ACD
【解析】
【分析】
取中点为,截面为等腰梯形,求其面积即可;平面过线段的中点,即可作出判断;过点分别做与平面,平面平行的平面,从而明确点的轨迹,得到长度.
【详解】
取中点为,易得,即截面为等腰梯形,
又
∴截面的面积是,故A正确;
连接,与交于点,则点为的中点,
而平面过线段的中点,
∴点和点到平面的距离相等,故B错误;
取的中点为,取的中点为,连接,
易得平面平面,即点的轨迹为,且,故C正确;
同样易知平面平面,即点的轨迹为,且,故D正确;
故选:ACD
12.ABD
【解析】
【分析】
取中点由已知条件可得平面,平面可判断A;
求出正四面体表面积可判断B;
由A选项得知,平面,取中点,连接,求出,可得四面体的体积可判断C;
将正四面体补成正方体,正方体的对角线即为外接球的直径,正四面体的棱长即为正方体面对角线长,计算出正方体对角线长可求出外接球的半径可判断D.
【详解】
对于A,取中点,连接,因为是正四面体,所以,且,所以平面,
平面,所以,故正确;
正四面体的一个侧面的面积为,
所以表面积为,故B正确;
由A选项得知,平面,取中点,连接,
因为是正四面体,所以,,,
所以,四面体的体积为,故C错误;
将正四面体补成正方体,则正四面体和长方体有相同的外接球,
正方体的对角线即为外接球的直径,正四面体的棱长即为正方体面对角线长,
因为正四面体的棱长为,所以正方体的棱长为,
对角线长为,
所以外接球的半径为 ,故D正确.
故选:ABD.
13.
【解析】
【分析】
利用勾股定理可求得球心到平面的距离,计算出三棱锥的高的最大值,利用锥体的体积公式可求出三棱锥体积的最大值.
【详解】
,所以,为截面圆的直径.
因为,,所以.
由球的性质可知圆面,即为球心到平面的距离.
在中,,,可得,
所以到平面的距离为.
要使三棱锥的体积最大,应为的延长线与球面的交点,
此时点到平面的距离为,
所以三棱锥体积的最大值为.
故答案为:;.
【点睛】
方法点睛:求空间几何体体积的方法如下:
(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;
(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.
14.
【解析】
【分析】
首先根据复数的几何意义得到,再求即可.
【详解】
因为复数,在复平面内的对应点关于虚轴对称,且,
所以.
所以.
故答案为:
15.
【解析】
【分析】
在上取一点,使得,在上一点,使得取,证得四边形为平行四边形,,进而结合平面图形的几何性质即可求出结果.
【详解】
在上取一点,使得,在上一点,使得取,又因为,则,所以四边形为平行四边形,所以,因为,则,,则,
所以.
故答案为:
16.
【解析】
【分析】
由,可得,再根据平面向量数量积的运算律计算可得;
【详解】
解:因为,所以,即,所以,所以,解得.
故答案为:
17.(1)0.25;(2)不是,理由见解析;(3)公平,理由见解析.
【解析】
【分析】
(1)根据基本事件总数,写出事件A包含的基本事件,即可得解;
(2)事件B与C可以同时发生,所以他们不是互斥事件;
(3)分别计算甲乙赢得比赛的概率进行判断.
【详解】
(1)易知样本点总数n=16,且每个样本点出现的可能性相等.
事件A包含的样本点共4个:(1,4),(2,3),(3,2),(4,1),
所以P(A)=0.25
(2)B与C不是互斥事件
理由:因为事件B与C可以同时发生,如甲赢一次,乙赢两次
(3)这种游戏规则公平.理由如下:
和为偶数的样本点有:(1,1),(1,3), (2,2),(2,4),(3,1),(3,3), (4,2),(4,4),共8个,
所以甲赢的概率为0.5,乙赢的概率为0.5,所以这种游戏规则公平.
18.(1)
(2)
(3)
【解析】
【分析】
(1),利用共线向量的坐标表示即可求解;
(2),利用向量加法的坐标表示即可求解;
(3)根据题意得,即可求解.
(1)
,
因为,,三点共线,所以存在实数,使得,
即,得.
因为,是平面内两个不共线的非零向量,所以解得,.
(2)
(3)
因为,,,四点按顺时针顺序构成平行四边形,所以,设,所以,因为,
所以,解得,所以
19.(1);(2)
【解析】
【分析】
(1)设为与交点,则平面,进而根据几何关系得,再计算几何体的体积即可;
(2)根据圆台的体积与球的体积公式求解即可.
【详解】
解:(1)如图,正四棱锥中,设为与交点,
所以由正四棱锥的性质得平面,所以,
因为正四棱锥的底面边长是6,侧棱长为5,
所以,,
所以,即正四棱锥的高为
所以,该正四棱锥的体积为
(2)根据题意,图中阴影部分绕AB旋转一周所形成的几何体为圆台中挖去一个半径为的半球构成的组合体.
因为圆台的体积为,半球的体积为,
所以,所求几何体的体积为.
20.(1);
(2).
【解析】
【分析】
(1)根据复数的除法运算,化简,即可求解;
(2)利用复数相等的条件,列出方程,即可求解.
(1)
因为,可得
又为实数,可得,
解得,
所以.
(2)
因为是关于的方程的根,
所以,即,
可得,
解得.
21.(1);
(2)0.35;
(3)列联表答案见解析,没有99.9%的把握认为比赛成绩优秀与性别有关.
【解析】
【分析】
(1)利用频率分布直方图中各小矩形面积和为1求出a作答.
(2)求出比赛成绩不低于80分的频率,由频率估计概率即可作答.
(3)完善列联表,计算的观测值并与临界值表比对作答.
(1)由频率分布直方图知,,解得:,所以a的值是0.025.
(2)由(1)知,则比赛成绩不低于80分的频率为,所以从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分的概率约为0.35.
(3)由(2)知,在抽取的100名学生中,比赛成绩优秀的有人,由此可得完整的2×2列联表:
优秀 非优秀 合计
男生 10 40 50
女生 25 25 50
合计 35 65 100
零假设:比赛成绩优秀与性别无关,根据表中的数据,计算得到,依据小概率值的独立性检验,没有充分证据推断不成立,因此可以认为成立,即没有99.9%的把握认为比赛成绩优秀与性别有关.
22.(1)证明见解析;
(2)9.
【解析】
【分析】
(1)由面面垂直的性质得平面,再根据线面垂直、菱形及等边三角形性质可得,进而有,最后由线面垂直的判定证结论.
(2)由线面平行判定有面,则到面的距离相等,根据线面垂直有到面的距离为,最后由及棱锥的体积公式求体积.
(1)
因为面面,面面,面,
所以平面,平面,则.
在菱形中,为线段的中点,,易证:.
因为,所以.
因为,面,所以面.
(2)
由是矩形,即,面,面,
所以面,故到面的距离相等,
由(1)知:平面,故到面的距离为,
又,则.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.小明跟父母 爷爷和奶奶一同参加《中国诗词大会》的现场录制,5人坐一排.则小明的父母都与他相邻的概率为( )
A. B. C. D.
2.甲、乙两人独立地破译1个密码,他们能译出密码的概率分别为和,则两人合作译出密码的概率为( ).
A. B. C. D.
3.已知复数(其中i为虚数单位,)在复平面内对应的点为,则实数a的值为( )
A.1 B.2 C. D.0
4.正方体ABCD-A1B1C1D1中,M、N分别为棱AB,DD1中点,则异面直线A1M与C1N所成的角是( )
A.0 B. C. D.
5.河北定州中学数学建模社团开展劳动实习,学习加工制作糖果包装盒.现有一张边长为10的正六边形硬纸片,如图所示,裁掉阴影部分,然后按虚线处折成底面边长为6的正六棱柱无盖包装盒,则此包装盒的体积为( )
A.648 B.324 C.162 D.108
6.在中,角,,所对应的边分别是,,,若,,则的面积为( )
A. B.1 C. D.2
7.在中,角所对的边为,若,则( )
A. B. C. D.2
8.已知圆锥的两条母线,且SA与SB的夹角,的面积为,圆锥的母线SA与圆锥的底面圆O所成的角为,则圆锥的体积为( )
A. B. C. D.
二、多选题
9.给出以下关于斜二测直观图的结论,其中正确的是( )
A.水平放置的角的直观图一定是角 B.相等的角在直观图中仍然相等
C.相等的线段在直观图中仍然相等 D.两条平行线段在直观图中仍是平行线段
10.已知甲罐中有四个相同的小球,标号分别为1,2,3,4,乙罐中有五个相同的小球,标号分别为1,2,3,5,6.现从甲罐 乙罐中分别随机抽取1个小球,记事件“抽取的两个小球标号之和大于5”,事件“抽取的两个小球标号之积大于8”,则( )
A.事件发生的概率为 B.事件发生的概率为
C.事件发生的概率为 D.至少抽到一个有标号为3的小球的概率为
11.已知正方体的棱长为2,点分别是棱的中点,点在四边形内(包括边界)运动,则下列说法正确的是( )
A.截面的面积是
B.点和点到平面的距离不相等
C.若平面,则点的轨迹的长度是
D.若平面,则点的轨迹的长度是
12.已知正四面体的棱长为,则( ).
A. B.四面体的表面积为
C.四面体的体积为 D.四面体的外接球半径为
三、双空题
13.已知半径为的球面上有、、、四点,满足,,,则球心到平面的距离为___________,三棱锥体积的最大值为___________.
四、填空题
14.设复数,在复平面内的对应点关于虚轴对称,且(为虚数单位),则______.
15.已知为所在平面内一点,且满足,则的面积与的面积之比为_________.
16.已知在中,,,,点P为所在平面内一点,且. 若,则实数_______.
五、解答题
17.甲、乙两人玩一种猜数游戏,每次由甲、乙各出1到4中的一个数,若两个数的和为偶数算甲赢,否则算乙赢.
(1)若事件A表示“两个数的和为5”,求P(A);
(2)现连玩三次,若事件B表示“甲至少赢一次”,事件C表示“乙至少赢两次”,试问B与C是不是互斥事件 为什么
(3)这种游戏规则公平吗 试说明理由.
18.已知,是平面内两个不共线的非零向量,,,,且,,三点共线.
(1)求实数的值;
(2)若,,求的坐标;
(3)已知,在(2)的条件下,若,,,四点按顺时针顺序构成平行四边形,求点的坐标.
19.(1)已知正四棱锥的底面边长是6,侧棱长为5,求该正四棱锥的体积
(2)如图(单位:cm),求下图中阴影部分绕AB旋转一周所形成的几何体的体积.
20.已知复数是实数.
(1)求复数;
(2)若复数是关于的方程的根,求实数和的值.
21.为过接2022年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动,现从参加冬奥知识竞赛活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)为6组:,,,,,,得到如图所示的频率分布直方图.
(1)求a的值;
(2)记A表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分”,估计A的概率;
(3)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成低于90分为“非优秀”,请将下面的列联表补充完整,并判断是否有99.9%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 非优秀 合计
男生 40
女生 50
合计 100
参考公式及数据:,.
0.10 0.05 0.025 0.01 0.005 0.001
2.706 3.841 5.024 6.635 7.879 10.828
22.如图,平面平面,在矩形中,,四边形为菱形,为线段的中点,.
(1)证明:平面.
(2)求三棱锥的体积.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【解析】
【分析】
利用捆绑法求出排列数,进而可得概率.
【详解】
将小明父母与小明三人进行捆绑,其中小明居于中间,形成一个元素,与其他两个元素进行排序,则,
故所求的概率为,
故选:.
2.D
【解析】
【分析】
利用独立事件乘法公式、互斥事件的加法公式求两人合作译出密码的概率即可.
【详解】
由题意,两人合作译出密码的概率.
故选:D
3.A
【解析】
【分析】
先利用复数的乘法化简,再利用复数的几何意义求解.
【详解】
因为,
又因为复数在复平面内对应的点为,
所以,
解得
故选:A
4.D
【解析】
【分析】
取的中点,连接,交于,则可证得∥,则或其补角为异面直线A1M与C1N所成的角,然后由≌,可求出的大小
【详解】
取的中点,连接,交于,
因为N为DD1中点,
所以,∥,
所以四边形为平行四边形,
所以∥,
所以或其补角为异面直线A1M与C1N所成的角,
因为M为AB中点,为的中点,,
所以,
因为,
所以≌,
所以,
因为,
所以,
所以,
所以异面直线A1M与C1N所成的角是,
故选:D
5.B
【解析】
【分析】
利用正六边形的性质求出正六棱柱的高,再根据棱柱的体积:即可求解.
【详解】
如图:由正六边形的每个内角为,
按虚线处折成底面边长为6的正六棱柱,即,
所以 ,即正六棱柱的高为
所以正六棱柱体积:.
故选:B
6.A
【解析】
【分析】
利用正弦定理可出角,进而可得角,再利用三角形面积公式求解即可.
【详解】
在中,由正弦定理,得,即,所以,
又,所以,所以,
所以的面积.
故选: A
7.D
【解析】
【分析】
先求出的值,然后根据正弦定理进行边化角即可求出.
【详解】
因为,所以,
所以由正弦定理,得,所以,
所以.
故选:D.
8.B
【解析】
【分析】
由三角形的面积计算出边长,然后根据圆锥的母线SA与圆锥的底面圆O所成的角为得出高,由圆锥的体积公式即可得出结果.
【详解】
由圆锥的两条母线,,可得三角形的面积为:,.
设圆锥的高为h,底面圆O的半径为R,由圆锥的母线SA与圆锥的底面圆O所成的角为,可得,,,
则圆锥的体积:,
故选:B
9.AD
【解析】
【分析】
根据直观图和斜二测画法的规则,判断选项.
【详解】
水平放置的角的直观图一定是角,故A正确;角的大小在直观图中都会发生改变,有的线段在直观图中也会改变,比如正方形的直方图中,故BC错误;
由斜二测画法规则可知,直观图保持线段的平行性,所以D正确.
故选:AD
10.BCD
【解析】
【分析】
根据题意分别列出事件A和事件B所包含的基本事件,再逐个选项判定,即可求解.
【详解】
由题意知,从甲罐,乙罐中分别随机抽取1个小球,共有个基本事件,
其中事件A包含的基本事件有:
,共有11个基本事件;
事件B包含的基本事件有:,共有8个基本事件,
对于A中事件A发生的概率为,所以A不正确;
对于B中,由以上可得事件B是事件A的子事件,所以事件的概率为,
所以B正确;
对于C中,由事件B是事件A的子事件,所以事件概率为,所以C正确;
对于D中,可分为三种情况:当甲罐中抽到3,乙罐不是3时,有种;当甲罐不是3,乙罐是3时,有;当甲罐抽到3且乙罐也是3时,有1种,所以至少抽到一个有标号为3的小球的概率为,所以D正确.
故选:BCD.
11.ACD
【解析】
【分析】
取中点为,截面为等腰梯形,求其面积即可;平面过线段的中点,即可作出判断;过点分别做与平面,平面平行的平面,从而明确点的轨迹,得到长度.
【详解】
取中点为,易得,即截面为等腰梯形,
又
∴截面的面积是,故A正确;
连接,与交于点,则点为的中点,
而平面过线段的中点,
∴点和点到平面的距离相等,故B错误;
取的中点为,取的中点为,连接,
易得平面平面,即点的轨迹为,且,故C正确;
同样易知平面平面,即点的轨迹为,且,故D正确;
故选:ACD
12.ABD
【解析】
【分析】
取中点由已知条件可得平面,平面可判断A;
求出正四面体表面积可判断B;
由A选项得知,平面,取中点,连接,求出,可得四面体的体积可判断C;
将正四面体补成正方体,正方体的对角线即为外接球的直径,正四面体的棱长即为正方体面对角线长,计算出正方体对角线长可求出外接球的半径可判断D.
【详解】
对于A,取中点,连接,因为是正四面体,所以,且,所以平面,
平面,所以,故正确;
正四面体的一个侧面的面积为,
所以表面积为,故B正确;
由A选项得知,平面,取中点,连接,
因为是正四面体,所以,,,
所以,四面体的体积为,故C错误;
将正四面体补成正方体,则正四面体和长方体有相同的外接球,
正方体的对角线即为外接球的直径,正四面体的棱长即为正方体面对角线长,
因为正四面体的棱长为,所以正方体的棱长为,
对角线长为,
所以外接球的半径为 ,故D正确.
故选:ABD.
13.
【解析】
【分析】
利用勾股定理可求得球心到平面的距离,计算出三棱锥的高的最大值,利用锥体的体积公式可求出三棱锥体积的最大值.
【详解】
,所以,为截面圆的直径.
因为,,所以.
由球的性质可知圆面,即为球心到平面的距离.
在中,,,可得,
所以到平面的距离为.
要使三棱锥的体积最大,应为的延长线与球面的交点,
此时点到平面的距离为,
所以三棱锥体积的最大值为.
故答案为:;.
【点睛】
方法点睛:求空间几何体体积的方法如下:
(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系,利用相应体积公式求解;
(2)若所给几何体的体积不能直接利用公式得出,则常用等积法、分割法、补形法等方法进行求解.
14.
【解析】
【分析】
首先根据复数的几何意义得到,再求即可.
【详解】
因为复数,在复平面内的对应点关于虚轴对称,且,
所以.
所以.
故答案为:
15.
【解析】
【分析】
在上取一点,使得,在上一点,使得取,证得四边形为平行四边形,,进而结合平面图形的几何性质即可求出结果.
【详解】
在上取一点,使得,在上一点,使得取,又因为,则,所以四边形为平行四边形,所以,因为,则,,则,
所以.
故答案为:
16.
【解析】
【分析】
由,可得,再根据平面向量数量积的运算律计算可得;
【详解】
解:因为,所以,即,所以,所以,解得.
故答案为:
17.(1)0.25;(2)不是,理由见解析;(3)公平,理由见解析.
【解析】
【分析】
(1)根据基本事件总数,写出事件A包含的基本事件,即可得解;
(2)事件B与C可以同时发生,所以他们不是互斥事件;
(3)分别计算甲乙赢得比赛的概率进行判断.
【详解】
(1)易知样本点总数n=16,且每个样本点出现的可能性相等.
事件A包含的样本点共4个:(1,4),(2,3),(3,2),(4,1),
所以P(A)=0.25
(2)B与C不是互斥事件
理由:因为事件B与C可以同时发生,如甲赢一次,乙赢两次
(3)这种游戏规则公平.理由如下:
和为偶数的样本点有:(1,1),(1,3), (2,2),(2,4),(3,1),(3,3), (4,2),(4,4),共8个,
所以甲赢的概率为0.5,乙赢的概率为0.5,所以这种游戏规则公平.
18.(1)
(2)
(3)
【解析】
【分析】
(1),利用共线向量的坐标表示即可求解;
(2),利用向量加法的坐标表示即可求解;
(3)根据题意得,即可求解.
(1)
,
因为,,三点共线,所以存在实数,使得,
即,得.
因为,是平面内两个不共线的非零向量,所以解得,.
(2)
(3)
因为,,,四点按顺时针顺序构成平行四边形,所以,设,所以,因为,
所以,解得,所以
19.(1);(2)
【解析】
【分析】
(1)设为与交点,则平面,进而根据几何关系得,再计算几何体的体积即可;
(2)根据圆台的体积与球的体积公式求解即可.
【详解】
解:(1)如图,正四棱锥中,设为与交点,
所以由正四棱锥的性质得平面,所以,
因为正四棱锥的底面边长是6,侧棱长为5,
所以,,
所以,即正四棱锥的高为
所以,该正四棱锥的体积为
(2)根据题意,图中阴影部分绕AB旋转一周所形成的几何体为圆台中挖去一个半径为的半球构成的组合体.
因为圆台的体积为,半球的体积为,
所以,所求几何体的体积为.
20.(1);
(2).
【解析】
【分析】
(1)根据复数的除法运算,化简,即可求解;
(2)利用复数相等的条件,列出方程,即可求解.
(1)
因为,可得
又为实数,可得,
解得,
所以.
(2)
因为是关于的方程的根,
所以,即,
可得,
解得.
21.(1);
(2)0.35;
(3)列联表答案见解析,没有99.9%的把握认为比赛成绩优秀与性别有关.
【解析】
【分析】
(1)利用频率分布直方图中各小矩形面积和为1求出a作答.
(2)求出比赛成绩不低于80分的频率,由频率估计概率即可作答.
(3)完善列联表,计算的观测值并与临界值表比对作答.
(1)由频率分布直方图知,,解得:,所以a的值是0.025.
(2)由(1)知,则比赛成绩不低于80分的频率为,所以从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于80分的概率约为0.35.
(3)由(2)知,在抽取的100名学生中,比赛成绩优秀的有人,由此可得完整的2×2列联表:
优秀 非优秀 合计
男生 10 40 50
女生 25 25 50
合计 35 65 100
零假设:比赛成绩优秀与性别无关,根据表中的数据,计算得到,依据小概率值的独立性检验,没有充分证据推断不成立,因此可以认为成立,即没有99.9%的把握认为比赛成绩优秀与性别有关.
22.(1)证明见解析;
(2)9.
【解析】
【分析】
(1)由面面垂直的性质得平面,再根据线面垂直、菱形及等边三角形性质可得,进而有,最后由线面垂直的判定证结论.
(2)由线面平行判定有面,则到面的距离相等,根据线面垂直有到面的距离为,最后由及棱锥的体积公式求体积.
(1)
因为面面,面面,面,
所以平面,平面,则.
在菱形中,为线段的中点,,易证:.
因为,所以.
因为,面,所以面.
(2)
由是矩形,即,面,面,
所以面,故到面的距离相等,
由(1)知:平面,故到面的距离为,
又,则.
答案第1页,共2页
答案第1页,共2页
同课章节目录
