8.2代入消元法 教案
图片预览
文档简介
中小学教育资源及组卷应用平台
第八章“二元一次方程组”备课
一、主要内容及课时
8.1 二元一次方程组(1课时)8.2 消元( 4课时)
8.3 再探实际问题和二元一次方程组 (3课时) 小结 ( 2课时)
二、学习目标
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数的问题的数学模型.
2.了解二元一次方程及其相关概念,能设两个未知数并列方程组表示实际问题中的两种相关的等量关系.
3.了解解二元方程组的基本目标(使方程组逐步转化为x=a, 的形式),体会“消元”思想,掌握解二元一次方程组的代入法和加减法,能根据二元一次方程组的具体形式选择适当的解法.
4.通过探究实际问题,进一步认识利用二元一次方程组解决问题的基本过程,体会数学的应用价值,提高分析问题、解决问题的能力.
三、本章知识结构
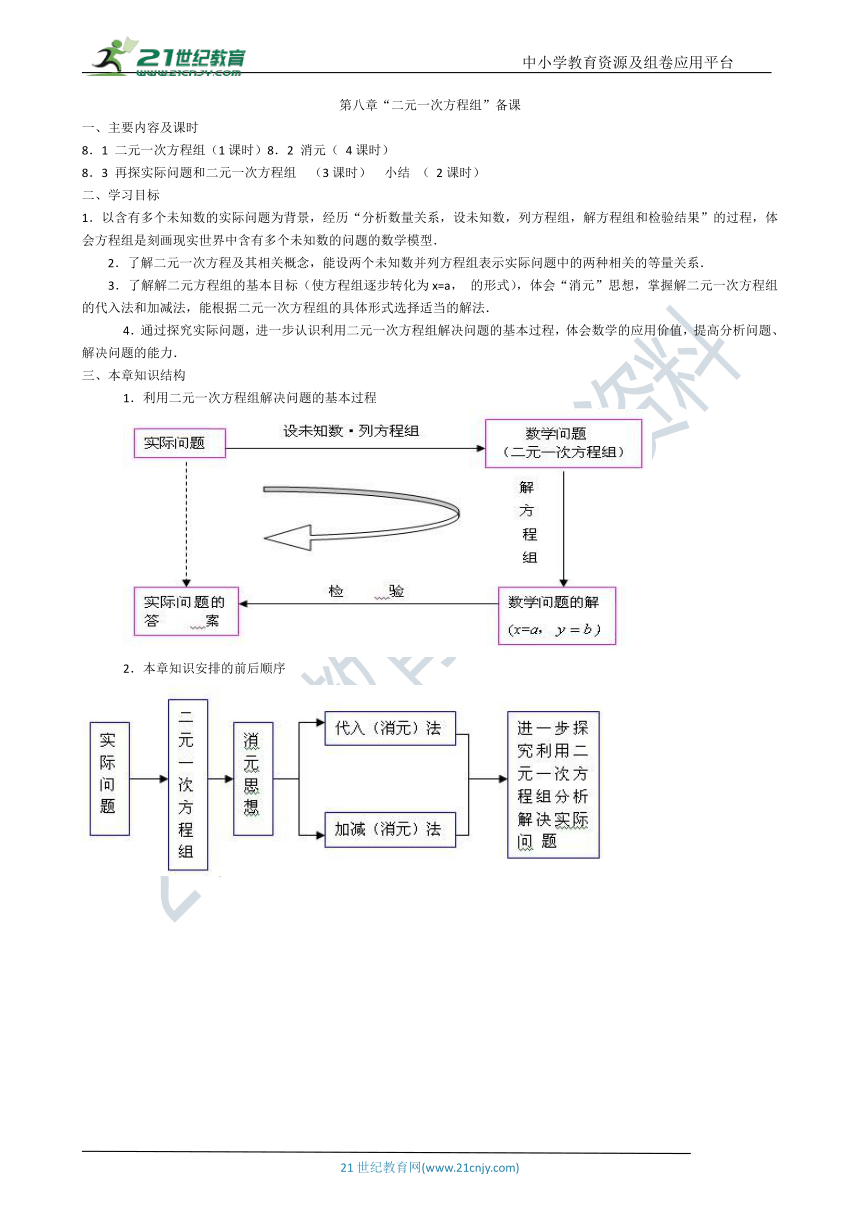
1.利用二元一次方程组解决问题的基本过程
2.本章知识安排的前后顺序
教学题目:代入消元法 总课时: 9课时 时间:
课标要求 体会解二元一次方程组的基本思想----“消元”。
内容与学情分析 内容分析 本节课是第八章的重要内容。本章的知识是反应客观世界数量关系的有效模型,所以掌握其基本的解法,不仅能使学生理解并掌握方程思想、转化思想、代入法等重要数学思想方法,从而初步培养学生的运算技能、应用意识,甚至对于提高分析并解决简单的实际问题有重要的意义。
学习目标 1.用代入法解二元一次方程组. 2.了解解二元一次方程组时的“消元”思想和“化未知为已知”的化归思想. 3.会用二元一次方程组解决实际问题.
学习重点 用代入法解二元一次方程组.
学习难点 探索如何用代入法将“二元”转化为“一元”的消元过程
学情分析 七年级学生的抽象思维能力和逻辑思维能力较差,运算能力不强,但是他们的好奇心强,具有一定的探究能力。教学中要根据学生实际情况,紧密联系学生已有知识,创设适宜的问题情境调动学生的主动性,进行必要的实践练习活动。
教学方法 启发式、自主探究式、讨论式以及讲练结合
教具器材 课件
第 3 课时目标 会用代入法解二元一次方程组.初步体会解二元一次方程组的基本思想――“消元”.
学生提前需要做的准备工作 解一元一次方程。
学习策略 采用“观察-分析-归纳-应用”的探究式的学习方式。
学习环节 学习任务设计与教师活动 学生活动设计 设计意图 落实目标
导入新课 一、创设情境,引入新课 教师出示下列问题: 问题1:篮球联赛中,每场比赛都要分胜负,每队胜一场得2分,负一场得1分.某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少? 在上述问题中,我们也可以设出两个未知数,列出二元一次方程组,那么怎样求解二元一次方程组呢? 学生板演列一元一次方程和二元一次方程组。 通过问题引起学生注意,同时把学生带入新课的学习情境中,激发学生求知欲望。
环节一 二、尝试活动,探索新知 教师引导: 什么是二元一次方程组的解?(方程组中各个方程的公共解) 师:这种列举法比较麻烦,有没有简单一点的方法呢? 这种通过代入消去一个未知数,使二元方程转化为一元方程,从而方程组得以求解的方法叫做代入消元法,简称代入法. .三、例题讲解 【例1】 用代入法解方程组 x-y=3, ①3x-8y=14. ②) 【例2】 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2∶5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶? 学生列式计算后回答:x+y=22, ①,2x+y=40. ②) 这两个方程的公共解是x=18,y=4.) 这样归纳后,学生对解方程组的思路就比较清晰,能够顺利实现目标同时也会对这种方法表现极大的兴趣。
环节二 四、巩固练习 1.二元一次方程组x-y=-3,2x+y=0)的解是( ) A.x=-1,y=2) B.x=1,y=-2) C.x=-1,y=-2) D.x=-2,y=1) 2.方程组x+3y=4,2x-3y=-1)的解是( ) A.x=-1,y=-1) B.x=1,y=1) C.x=-2,y=2) D.x=-2,y=-1)
环节三 五、课堂小结 你从本节课的学习中体会到代入法的基本思路是什么?主要步骤有哪些?让学生在互相交流的活动中完成本节课的小结,并能通过总结与归纳,更加清楚地理解代入消元法,体会代入消元法在解二元一次方程组的过程中反映出来的化归思想.
达标检测 数学书93页1、2题
作业布置 数学书111页1题。
板书设计 代入消元法 这种通过代入消去一个未知数,使二元方程转化为一元方程,从而方程组得以求解的方法叫做代入消元法,简称代入法.
教学反思
21世纪教育网(www.21cnjy.com)
第八章“二元一次方程组”备课
一、主要内容及课时
8.1 二元一次方程组(1课时)8.2 消元( 4课时)
8.3 再探实际问题和二元一次方程组 (3课时) 小结 ( 2课时)
二、学习目标
1.以含有多个未知数的实际问题为背景,经历“分析数量关系,设未知数,列方程组,解方程组和检验结果”的过程,体会方程组是刻画现实世界中含有多个未知数的问题的数学模型.
2.了解二元一次方程及其相关概念,能设两个未知数并列方程组表示实际问题中的两种相关的等量关系.
3.了解解二元方程组的基本目标(使方程组逐步转化为x=a, 的形式),体会“消元”思想,掌握解二元一次方程组的代入法和加减法,能根据二元一次方程组的具体形式选择适当的解法.
4.通过探究实际问题,进一步认识利用二元一次方程组解决问题的基本过程,体会数学的应用价值,提高分析问题、解决问题的能力.
三、本章知识结构
1.利用二元一次方程组解决问题的基本过程
2.本章知识安排的前后顺序
教学题目:代入消元法 总课时: 9课时 时间:
课标要求 体会解二元一次方程组的基本思想----“消元”。
内容与学情分析 内容分析 本节课是第八章的重要内容。本章的知识是反应客观世界数量关系的有效模型,所以掌握其基本的解法,不仅能使学生理解并掌握方程思想、转化思想、代入法等重要数学思想方法,从而初步培养学生的运算技能、应用意识,甚至对于提高分析并解决简单的实际问题有重要的意义。
学习目标 1.用代入法解二元一次方程组. 2.了解解二元一次方程组时的“消元”思想和“化未知为已知”的化归思想. 3.会用二元一次方程组解决实际问题.
学习重点 用代入法解二元一次方程组.
学习难点 探索如何用代入法将“二元”转化为“一元”的消元过程
学情分析 七年级学生的抽象思维能力和逻辑思维能力较差,运算能力不强,但是他们的好奇心强,具有一定的探究能力。教学中要根据学生实际情况,紧密联系学生已有知识,创设适宜的问题情境调动学生的主动性,进行必要的实践练习活动。
教学方法 启发式、自主探究式、讨论式以及讲练结合
教具器材 课件
第 3 课时目标 会用代入法解二元一次方程组.初步体会解二元一次方程组的基本思想――“消元”.
学生提前需要做的准备工作 解一元一次方程。
学习策略 采用“观察-分析-归纳-应用”的探究式的学习方式。
学习环节 学习任务设计与教师活动 学生活动设计 设计意图 落实目标
导入新课 一、创设情境,引入新课 教师出示下列问题: 问题1:篮球联赛中,每场比赛都要分胜负,每队胜一场得2分,负一场得1分.某队为了争取较好的名次,想在全部22场比赛中得到40分,那么这个队胜负场数分别是多少? 在上述问题中,我们也可以设出两个未知数,列出二元一次方程组,那么怎样求解二元一次方程组呢? 学生板演列一元一次方程和二元一次方程组。 通过问题引起学生注意,同时把学生带入新课的学习情境中,激发学生求知欲望。
环节一 二、尝试活动,探索新知 教师引导: 什么是二元一次方程组的解?(方程组中各个方程的公共解) 师:这种列举法比较麻烦,有没有简单一点的方法呢? 这种通过代入消去一个未知数,使二元方程转化为一元方程,从而方程组得以求解的方法叫做代入消元法,简称代入法. .三、例题讲解 【例1】 用代入法解方程组 x-y=3, ①3x-8y=14. ②) 【例2】 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2∶5.某厂每天生产这种消毒液22.5 t,这些消毒液应该分装大、小瓶两种产品各多少瓶? 学生列式计算后回答:x+y=22, ①,2x+y=40. ②) 这两个方程的公共解是x=18,y=4.) 这样归纳后,学生对解方程组的思路就比较清晰,能够顺利实现目标同时也会对这种方法表现极大的兴趣。
环节二 四、巩固练习 1.二元一次方程组x-y=-3,2x+y=0)的解是( ) A.x=-1,y=2) B.x=1,y=-2) C.x=-1,y=-2) D.x=-2,y=1) 2.方程组x+3y=4,2x-3y=-1)的解是( ) A.x=-1,y=-1) B.x=1,y=1) C.x=-2,y=2) D.x=-2,y=-1)
环节三 五、课堂小结 你从本节课的学习中体会到代入法的基本思路是什么?主要步骤有哪些?让学生在互相交流的活动中完成本节课的小结,并能通过总结与归纳,更加清楚地理解代入消元法,体会代入消元法在解二元一次方程组的过程中反映出来的化归思想.
达标检测 数学书93页1、2题
作业布置 数学书111页1题。
板书设计 代入消元法 这种通过代入消去一个未知数,使二元方程转化为一元方程,从而方程组得以求解的方法叫做代入消元法,简称代入法.
教学反思
21世纪教育网(www.21cnjy.com)
