人教版七年级上册4.3.3余角和补角课件(共22张PPT)
文档属性
| 名称 | 人教版七年级上册4.3.3余角和补角课件(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 446.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
4.3.3 余角和补角
七年级-上册-第四章第三节
本课重点
余角、补角
性质
概念
情境引入
N
O
D
C
4
1
3
2
A
B
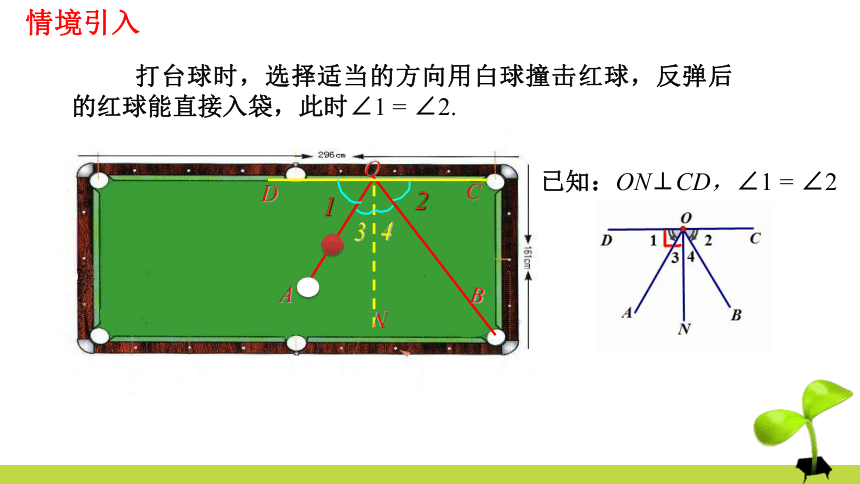
打台球时,选择适当的方向用白球撞击红球,反弹后的红球能直接入袋,此时∠1 = ∠2.
已知:ON⊥CD,∠1 = ∠2
1.概念
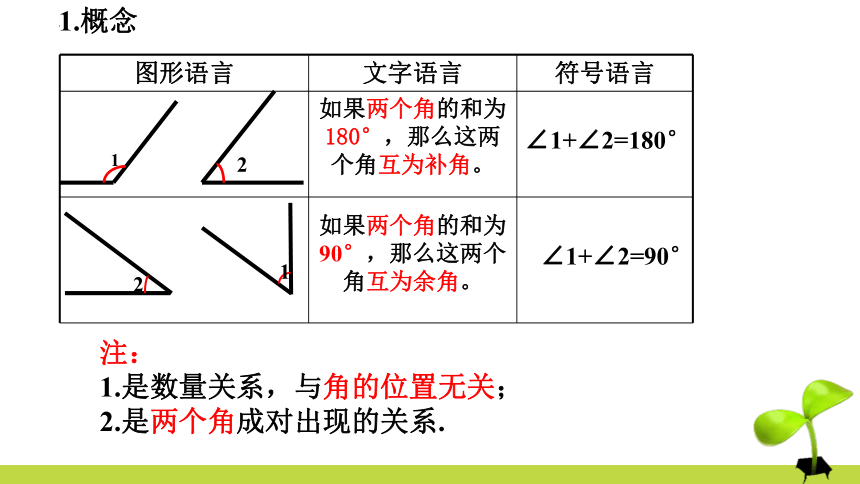
图形语言 文字语言 符号语言
如果两个角的和为180°,那么这两个角互为补角。
∠1+∠2=180°
1
2
2
1
如果两个角的和为 90°,那么这两个角互为余角。
∠1+∠2=90°
相关问题:
①如果三个角、四个角的和为180°,称互补?有无特殊名称?
②互余、互补有位置限定吗?如公共端点?如在同一平面内?
如果两个角的和为180°,那么这两个角互为补角。
如果两个角的和为 90°,那么这两个角互为余角。
1.概念
1.概念
图形语言 文字语言 符号语言
如果两个角的和为180°,那么这两个角互为补角。
∠1+∠2=180°
1
2
2
1
如果两个角的和为 90°,那么这两个角互为余角。
∠1+∠2=90°
注:
1.是数量关系,与角的位置无关;
2.是两个角成对出现的关系.
练习
(1)30°,70°与80°的和为平角,所以这三个角互补。( )
(2)若∠1+∠2=90°,则∠1为余角。 ( )
(3)两角是否互补与其位置有关。( )
1.判断下列说法是否正确。
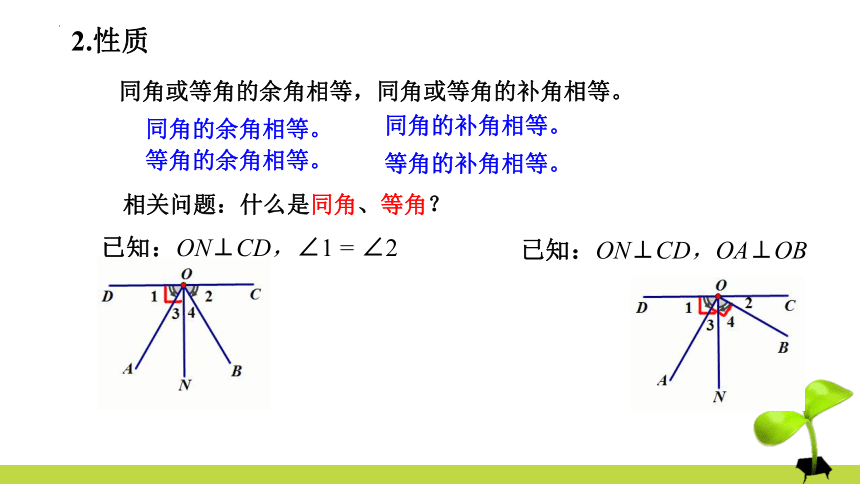
同角或等角的余角相等,同角或等角的补角相等。
同角的余角相等。
等角的余角相等。
同角的补角相等。
等角的补角相等。
相关问题:什么是同角、等角?
2.性质
已知:ON⊥CD,∠1 = ∠2
已知:ON⊥CD,OA⊥OB
练习
D
A
B
E
O
┐
┐
1
2
3
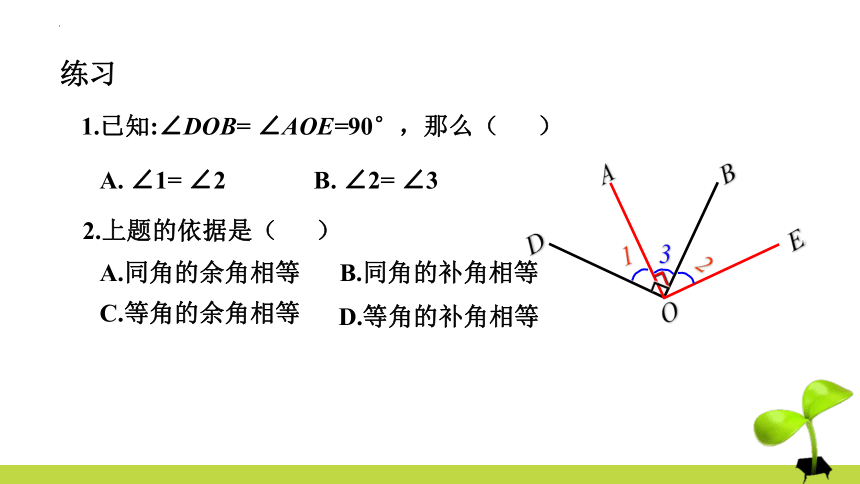
1.已知:∠DOB= ∠AOE=90°,那么( )
A. ∠1= ∠2 B. ∠2= ∠3
2.上题的依据是( )
A.同角的余角相等
C.等角的余角相等
B.同角的补角相等
D.等角的补角相等
余角补角小结
性质
概念
∠1+∠2=180°
∠1、∠2互为余角
∠1+∠2=90°
数量关系!
∠1、∠2互为补角
两个角!
同角或等角的余角相等,同角或等角的补角相等。
余角和补角性质的运用
12
如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进围墙,如何测量?
B
A
O
A
C
O
B
1
2
如果两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个角的补角.
几何语言表示为:
如果∠1+∠2=180°,那么∠1与∠2互为补角.
2
1
∠1+∠2=180°
知识讲解
如图∠AOD = 90°
∠1+∠2 = 90°
0
A
D
2.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角.
1
2
几何语言表示为:
如果∠1+∠2=90°,那么∠1与∠2互为余角.
∠1 +∠2 =90°
1
2
知识讲解
的度数
的余角
的补角
练一练
想一想:同一个角的补角与它的余角之间有怎样的数量关系?
的余角+ 90 = 的补角
分析: ∠AOB = 90 °则______+ ∠BOD = 90 °;
同角的余角相等
如图,∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
A
O
B
C
D
1
2
余角的性质
∠COD = 90 °则 _____+ ∠BOD = 90 °
答:∠1 = ∠2
∠1
∠2
探究一
知识讲解
知识讲解
2、如图,∠3和∠AOB互为补角,∠4和∠AOB也互为补角,请问
∠3 和∠4有什么数量关系?为什么?请尝试用简单的几何语言来
说理。
理由:
同角的补角相等
3、如图,如果∠1与∠2互为余角,
∠3与∠4互为余角,且∠1=∠4,那么∠2与∠3相等吗?为什么?请尝试用几何语言来说理
4、如图,如果∠A与∠B互为补角,
∠C与∠D互为补角,且∠A=∠C,
那么∠B与∠D相等吗?为什么?请
尝试用几何语言来说理
①用一句话概括结论。
①用一句话概括结论。
理由:
等角的余角相等
等角的补角相等
理由:
知识讲解
探究余角和补角的性质
余角的性质结论:
补角的性质结论:
总结成一句话:
同角或等角的余角相等;
同角或等角的补角相等。
如图,A、O、B在同一条直线上,∠AOD=∠COE=90°。
(1)图中与∠2互为余角的角有 ;
与∠1互为余角的角有 。
(2)请写出图中相等的锐角,并说明理由;
(3)∠1的补角是哪个角?∠2有补角吗?
∠2和∠4
∠1和∠3
∠1和∠3
∠2和∠4
由∠1+∠COB=180°,所以∠1的补角是∠COB
∵∠4+∠AOE=180°
∴∠2+∠AOE=180°
课堂练习
∴∠2的补角是∠AOE
∠1+∠2=90°
∠1+∠2=180°
同角或等角的余角相等
同角或等角的补角相等.
互 余 互 补
数量 关系
对 应 图 形
性 质
2
1
1
2
小结
谢谢聆听
4.3.3 余角和补角
七年级-上册-第四章第三节
本课重点
余角、补角
性质
概念
情境引入
N
O
D
C
4
1
3
2
A
B
打台球时,选择适当的方向用白球撞击红球,反弹后的红球能直接入袋,此时∠1 = ∠2.
已知:ON⊥CD,∠1 = ∠2
1.概念
图形语言 文字语言 符号语言
如果两个角的和为180°,那么这两个角互为补角。
∠1+∠2=180°
1
2
2
1
如果两个角的和为 90°,那么这两个角互为余角。
∠1+∠2=90°
相关问题:
①如果三个角、四个角的和为180°,称互补?有无特殊名称?
②互余、互补有位置限定吗?如公共端点?如在同一平面内?
如果两个角的和为180°,那么这两个角互为补角。
如果两个角的和为 90°,那么这两个角互为余角。
1.概念
1.概念
图形语言 文字语言 符号语言
如果两个角的和为180°,那么这两个角互为补角。
∠1+∠2=180°
1
2
2
1
如果两个角的和为 90°,那么这两个角互为余角。
∠1+∠2=90°
注:
1.是数量关系,与角的位置无关;
2.是两个角成对出现的关系.
练习
(1)30°,70°与80°的和为平角,所以这三个角互补。( )
(2)若∠1+∠2=90°,则∠1为余角。 ( )
(3)两角是否互补与其位置有关。( )
1.判断下列说法是否正确。
同角或等角的余角相等,同角或等角的补角相等。
同角的余角相等。
等角的余角相等。
同角的补角相等。
等角的补角相等。
相关问题:什么是同角、等角?
2.性质
已知:ON⊥CD,∠1 = ∠2
已知:ON⊥CD,OA⊥OB
练习
D
A
B
E
O
┐
┐
1
2
3
1.已知:∠DOB= ∠AOE=90°,那么( )
A. ∠1= ∠2 B. ∠2= ∠3
2.上题的依据是( )
A.同角的余角相等
C.等角的余角相等
B.同角的补角相等
D.等角的补角相等
余角补角小结
性质
概念
∠1+∠2=180°
∠1、∠2互为余角
∠1+∠2=90°
数量关系!
∠1、∠2互为补角
两个角!
同角或等角的余角相等,同角或等角的补角相等。
余角和补角性质的运用
12
如图,要测量两堵围墙所形成的∠AOB的度数,但人不能进围墙,如何测量?
B
A
O
A
C
O
B
1
2
如果两个角的和等于180°(平角),就说这两个角互为补角,简称互补,即其中一个角是另一个角的补角.
几何语言表示为:
如果∠1+∠2=180°,那么∠1与∠2互为补角.
2
1
∠1+∠2=180°
知识讲解
如图∠AOD = 90°
∠1+∠2 = 90°
0
A
D
2.如果两个角的和等于90°(直角),就说这两个角互为余角,简称互余,即其中一个角是另一个角的余角.
1
2
几何语言表示为:
如果∠1+∠2=90°,那么∠1与∠2互为余角.
∠1 +∠2 =90°
1
2
知识讲解
的度数
的余角
的补角
练一练
想一想:同一个角的补角与它的余角之间有怎样的数量关系?
的余角+ 90 = 的补角
分析: ∠AOB = 90 °则______+ ∠BOD = 90 °;
同角的余角相等
如图,∠AOB = 90 °
∠COD = 90 °
则∠1与∠2是什么关系?
A
O
B
C
D
1
2
余角的性质
∠COD = 90 °则 _____+ ∠BOD = 90 °
答:∠1 = ∠2
∠1
∠2
探究一
知识讲解
知识讲解
2、如图,∠3和∠AOB互为补角,∠4和∠AOB也互为补角,请问
∠3 和∠4有什么数量关系?为什么?请尝试用简单的几何语言来
说理。
理由:
同角的补角相等
3、如图,如果∠1与∠2互为余角,
∠3与∠4互为余角,且∠1=∠4,那么∠2与∠3相等吗?为什么?请尝试用几何语言来说理
4、如图,如果∠A与∠B互为补角,
∠C与∠D互为补角,且∠A=∠C,
那么∠B与∠D相等吗?为什么?请
尝试用几何语言来说理
①用一句话概括结论。
①用一句话概括结论。
理由:
等角的余角相等
等角的补角相等
理由:
知识讲解
探究余角和补角的性质
余角的性质结论:
补角的性质结论:
总结成一句话:
同角或等角的余角相等;
同角或等角的补角相等。
如图,A、O、B在同一条直线上,∠AOD=∠COE=90°。
(1)图中与∠2互为余角的角有 ;
与∠1互为余角的角有 。
(2)请写出图中相等的锐角,并说明理由;
(3)∠1的补角是哪个角?∠2有补角吗?
∠2和∠4
∠1和∠3
∠1和∠3
∠2和∠4
由∠1+∠COB=180°,所以∠1的补角是∠COB
∵∠4+∠AOE=180°
∴∠2+∠AOE=180°
课堂练习
∴∠2的补角是∠AOE
∠1+∠2=90°
∠1+∠2=180°
同角或等角的余角相等
同角或等角的补角相等.
互 余 互 补
数量 关系
对 应 图 形
性 质
2
1
1
2
小结
谢谢聆听
