一元一次不等式复习课[下学期]
文档属性
| 名称 | 一元一次不等式复习课[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 409.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-02-04 00:00:00 | ||
图片预览










文档简介
课件31张PPT。9.3一元一次不等式组教学设计:本节的重点是理解一元一次不等式组及其解集的意义,难点是解一元一次不等式组以及利用它解决实际问题,学习本节时应注意以下几点:
①两个一元一次不等式合在一起组成一个不等式组,要理解其解集是什么,即一元一次不等式组中各个不等式的解集的公共部分,叫做一元一次不等式组的解集;
②二元一次方程组的解通过消元直接产生,而一元一次不等式组的解集要借助画出数轴得出。一定要注意:如果不等式组中各个不等式的解集没有公共部分,那么这个不等式组无解;
③本节课的实际问题中数量间的大小关系相对于前面的几节课来说更为复杂,要正确、全面的理解问题情境,仔细的分析问题中的数量关系,通过解决实际问题进一步培养学生建立不等式(组)模型的能力。南方某市的一种出租车起步价是10元(即行驶距离在5km以内的都要付10元车费).达到或超过5km,每增加1km,加价1.2元(不足1km部分按1km算).现在小明乘坐这种出租车从家到学校,支付车费17.2元,你知道小明家离学校大约多远吗?
由于小明支付车费17.2元,已超过了起步价10元,说明汽车行驶的路程超过了5km,若设小明家到学校的路程大约为xkm,则此时x既要满足10+1.2(x-5)≤17.2,又要满足10+1.2(x-5)≥17.2-1.2,即x是两个不等式的公共解.与方程组类似,这里可以将约束x的两个不等式组成不等式组来表示同时满足的意义. 知识回顾
1、一元一次不等式组:
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
在理解时要注意以下两点:
1) 不等式组里不等式的个数并未规定;
2) 在同一不等式组里的未知数必须是同一个.2、一元一次不等式组的解集:
一元一次不等式组中,各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
注意:
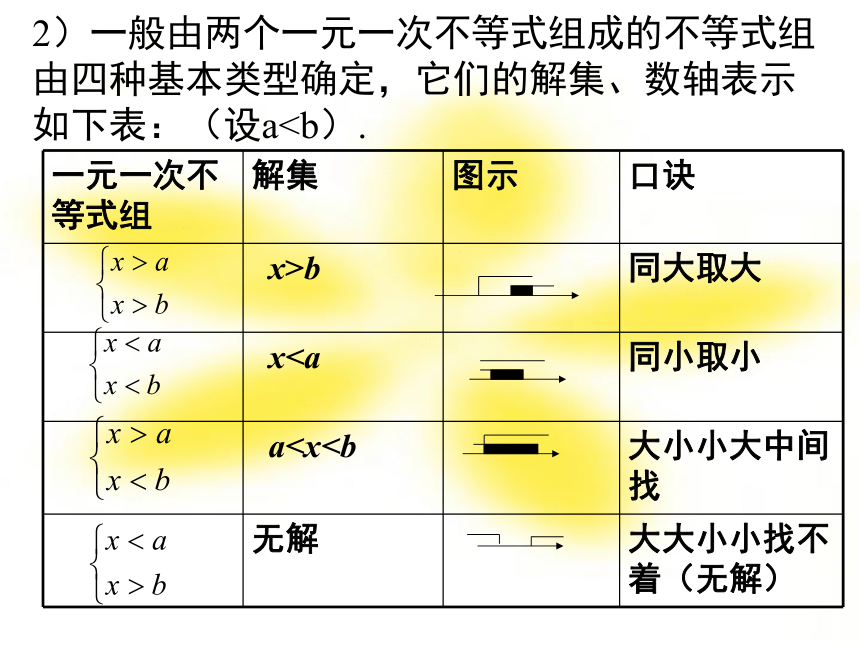
1) 求几个一元一次不等式的解集的公共部分,通常是利用数轴来确定的.公共部分是指数轴上被两条不等式解集的区域都覆盖的部分.2)一般由两个一元一次不等式组成的不等式组由四种基本类型确定,它们的解集、数轴表示如下表:(设a
①两个一元一次不等式合在一起组成一个不等式组,要理解其解集是什么,即一元一次不等式组中各个不等式的解集的公共部分,叫做一元一次不等式组的解集;
②二元一次方程组的解通过消元直接产生,而一元一次不等式组的解集要借助画出数轴得出。一定要注意:如果不等式组中各个不等式的解集没有公共部分,那么这个不等式组无解;
③本节课的实际问题中数量间的大小关系相对于前面的几节课来说更为复杂,要正确、全面的理解问题情境,仔细的分析问题中的数量关系,通过解决实际问题进一步培养学生建立不等式(组)模型的能力。南方某市的一种出租车起步价是10元(即行驶距离在5km以内的都要付10元车费).达到或超过5km,每增加1km,加价1.2元(不足1km部分按1km算).现在小明乘坐这种出租车从家到学校,支付车费17.2元,你知道小明家离学校大约多远吗?
由于小明支付车费17.2元,已超过了起步价10元,说明汽车行驶的路程超过了5km,若设小明家到学校的路程大约为xkm,则此时x既要满足10+1.2(x-5)≤17.2,又要满足10+1.2(x-5)≥17.2-1.2,即x是两个不等式的公共解.与方程组类似,这里可以将约束x的两个不等式组成不等式组来表示同时满足的意义. 知识回顾
1、一元一次不等式组:
一般地,关于同一未知数的几个一元一次不等式合在一起,就组成一个一元一次不等式组.
在理解时要注意以下两点:
1) 不等式组里不等式的个数并未规定;
2) 在同一不等式组里的未知数必须是同一个.2、一元一次不等式组的解集:
一元一次不等式组中,各个不等式的解集的公共部分,叫做这个一元一次不等式组的解集.
注意:
1) 求几个一元一次不等式的解集的公共部分,通常是利用数轴来确定的.公共部分是指数轴上被两条不等式解集的区域都覆盖的部分.2)一般由两个一元一次不等式组成的不等式组由四种基本类型确定,它们的解集、数轴表示如下表:(设a
