沪科版八年级下册19四边形小结与复习课件(共22张PPT)
文档属性
| 名称 | 沪科版八年级下册19四边形小结与复习课件(共22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 21:54:25 | ||
图片预览






文档简介
(共22张PPT)
第19章 四边形复习
一、多边形的内角和与外角和
多边形的内角和等于(n-2) ×180 °
多边形的外角和等于 360 °
正多边形每个内角的度数是
正多边形每个外角的度数是
知识梳理
1:已知一个多边形的每个外角都是其相邻内角度数的 ,求这个多边形的边数.
解: 设此多边形的外角的度数为x,则内角的度数为4x,
则x+4x=180°,解得 x=36°.
∴边数n=360°÷36°=10.
知识点巩固
考点一 多边形的内角和与外角和
1.一个正多边形的每一个内角都等于120 °,则其边数是 .
6
【解析】 因为该多边形的每一个内角都等于120度,所以它的每一个外角都等于60 °.所以边数是6.
在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用.尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数.
归纳拓展
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
二、平行四边形的性质
对角线互相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
2 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC
【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;
D
考点二 平行四边形的性质
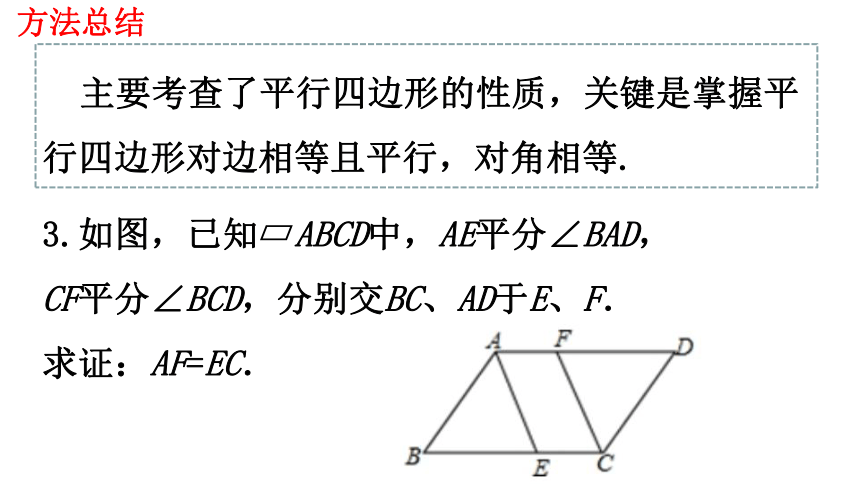
主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.
方法总结
3.如图,已知 ABCD中,AE平分∠BAD,
CF平分∠BCD,分别交BC、AD于E、F.
求证:AF=EC.
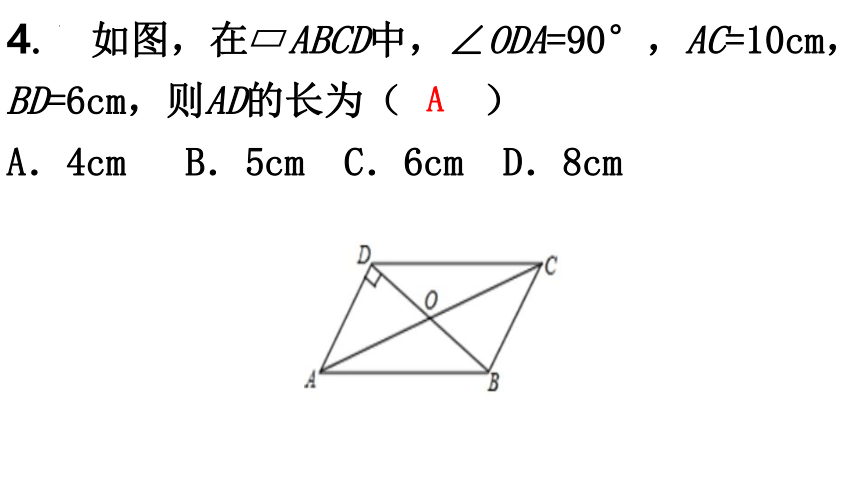
4. 如图,在 ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
A
几 何 语 言
文字叙述
两组对边相等
一组对边
平行且相等
∴四边形ABCD是平行四边形.
∵ AD=BC ,AB=DC,
∴ 四边形ABCD是平行四边形.
∵ AB=DC,AB∥DC,
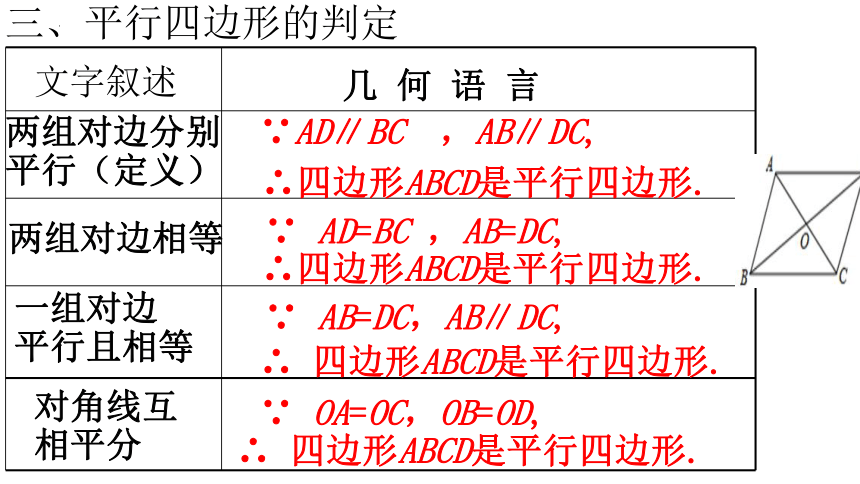
三、平行四边形的判定
对角线互相平分
∴ 四边形ABCD是平行四边形.
∵ OA=OC,OB=OD,
两组对边分别平行(定义)
∴四边形ABCD是平行四边形.
∵AD∥BC ,AB∥DC,
5. 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
考点三 平行四边形的判定
平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.
方法总结
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
四、三角形的中位线
用符号语言表示
∵DE是△ABC的中位线
∴DE∥BC,
6. 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点。
求证: .
A
B
C
D
E
F
H
考点四 三角形的中位线
项目 四边形 对边 角 对角线
平行且相等
平行
且四边相等
平行
且四边相等
四个角
都是直角
对角相等
邻角互补
四个角
都是直角
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
互相垂直且平分,每一条对角线平分一组对角
五、矩形、菱形、正方形的性质
四边形 条件
①定义:有一个角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形
六、矩形、菱形、正方形的判定方法
7.如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.
A
B
C
D
O
考点五 矩形的性质和判定
8.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
A
B
C
O
D
考点六 菱形的性质和判定
9.如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.
A
B
D
C
F
E
考点七 正方形的性质和判定
平 行 四 边 形
性质
①对边平行且相等
②对角相等,邻角互补
③对角线互相平分
判定
①两组对边分别平行的
②两组对边分别相等的
③一组对边平行且相等的
④对角线互相平分的
四 边 形
平 行 四 边 形
课堂小结
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
多边形的内角和与外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关
正多
边形
内角= ,外角=
5种识
别方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
一组邻边相等
对角线垂直
一个角是直角
对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
课后作业
书本A,B,C组相应习题
第19章 四边形复习
一、多边形的内角和与外角和
多边形的内角和等于(n-2) ×180 °
多边形的外角和等于 360 °
正多边形每个内角的度数是
正多边形每个外角的度数是
知识梳理
1:已知一个多边形的每个外角都是其相邻内角度数的 ,求这个多边形的边数.
解: 设此多边形的外角的度数为x,则内角的度数为4x,
则x+4x=180°,解得 x=36°.
∴边数n=360°÷36°=10.
知识点巩固
考点一 多边形的内角和与外角和
1.一个正多边形的每一个内角都等于120 °,则其边数是 .
6
【解析】 因为该多边形的每一个内角都等于120度,所以它的每一个外角都等于60 °.所以边数是6.
在多边形的有关求边数或内角、外角度数的问题中,要注意内角与外角之间的转化,以及定理的运用.尤其在求边数的问题中,常常利用定理列出方程,进而再求得边数.
归纳拓展
几 何 语 言
文字叙述
对边平行
对边相等
对角相等
∴ AD=BC ,AB=DC.
∵ 四边形ABCD是平行四边形,
∴ ∠ A=∠C,∠ B=∠D.
∵ 四边形ABCD是平行四边形,
二、平行四边形的性质
对角线互相平分
∵ 四边形ABCD是平行四边形,
∴ OA=OC,OB=OD.
∵ 四边形ABCD是平行四边形,
∴ AD∥BC ,AB∥DC.
2 如图,在平行四边形ABCD中,下列结论中错误的是( )
A.∠1=∠2 B.∠BAD=∠BCD
C.AB=CD D.AC=BC
【解析】A.∵四边形ABCD是平行四边形,
∴AB∥CD,∴∠1=∠2,故A正确;
B.∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD,故B正确;
C.∵四边形ABCD是平行四边形,
∴AB=CD,故C正确;
D
考点二 平行四边形的性质
主要考查了平行四边形的性质,关键是掌握平行四边形对边相等且平行,对角相等.
方法总结
3.如图,已知 ABCD中,AE平分∠BAD,
CF平分∠BCD,分别交BC、AD于E、F.
求证:AF=EC.
4. 如图,在 ABCD中,∠ODA=90°,AC=10cm,BD=6cm,则AD的长为( )
A.4cm B.5cm C.6cm D.8cm
A
几 何 语 言
文字叙述
两组对边相等
一组对边
平行且相等
∴四边形ABCD是平行四边形.
∵ AD=BC ,AB=DC,
∴ 四边形ABCD是平行四边形.
∵ AB=DC,AB∥DC,
三、平行四边形的判定
对角线互相平分
∴ 四边形ABCD是平行四边形.
∵ OA=OC,OB=OD,
两组对边分别平行(定义)
∴四边形ABCD是平行四边形.
∵AD∥BC ,AB∥DC,
5. 如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.∠BAD=∠BCD,AB∥CD
C.AD∥BC,AD=BC
D.AB=CD,AO=CO
D
考点三 平行四边形的判定
平行四边形的判定方法:
①两组对边分别平行的四边形是平行四边形;
②两组对边分别相等的四边形是平行四边形;
③两组对角分别相等的四边形是平行四边形;
④对角线互相平分的四边形是平行四边形;
⑤一组对边平行且相等的四边形是平行四边形.
方法总结
1.三角形的中位线定义:连结三角形两边中点的线段叫做三角形的中位线.
2.三角形的中位线性质:三角形的中位线平行于第三边,并且等于第三边的一半.
四、三角形的中位线
用符号语言表示
∵DE是△ABC的中位线
∴DE∥BC,
6. 已知:AD是△ABC的中线,E是AD的中点,F是BE的延长线与AC的交点。
求证: .
A
B
C
D
E
F
H
考点四 三角形的中位线
项目 四边形 对边 角 对角线
平行且相等
平行
且四边相等
平行
且四边相等
四个角
都是直角
对角相等
邻角互补
四个角
都是直角
互相平分且相等
互相垂直平分且相等,每一条对角线平分一组对角
互相垂直且平分,每一条对角线平分一组对角
五、矩形、菱形、正方形的性质
四边形 条件
①定义:有一个角是直角的平行四边形
②三个角是直角的四边形
③对角线相等的平行四边形
①定义:一组邻边相等的平行四边形
②四条边都相等的四边形
③对角线互相垂直的平行四边形
①定义:一组邻边相等且有一个角是直角的平行四边形
②有一组邻边相等的矩形
③有一个角是直角的菱形
六、矩形、菱形、正方形的判定方法
7.如图,在矩形ABCD中,两条对角线相交于点O,
∠AOD=120°,AB=2.5 ,求矩形对角线的长.
A
B
C
D
O
考点五 矩形的性质和判定
8.如图,在菱形ABCD中,对角线AC与BD相交于点O,∠BAD=60°,BD =6,求菱形的边长AB和对角线AC的长.
A
B
C
O
D
考点六 菱形的性质和判定
9.如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.
A
B
D
C
F
E
考点七 正方形的性质和判定
平 行 四 边 形
性质
①对边平行且相等
②对角相等,邻角互补
③对角线互相平分
判定
①两组对边分别平行的
②两组对边分别相等的
③一组对边平行且相等的
④对角线互相平分的
四 边 形
平 行 四 边 形
课堂小结
三角形的中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
多边形的内角和与外角和
内角和计算公式
(n-2) × 180 °(n ≥3的整数)
外角和
多边形的外角和等于360°
特别注意:与边数无关
正多
边形
内角= ,外角=
5种识
别方法
三个角是直角
四条边相等
一个角是直角
对角线相等
一组邻边相等
对角线垂直
一组邻边相等
对角线垂直
一个角是直角
对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
课后作业
书本A,B,C组相应习题
