4.3 空间直角坐标系与空间两点间的距离公式[上学期]
文档属性
| 名称 | 4.3 空间直角坐标系与空间两点间的距离公式[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 26.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-11-01 00:00:00 | ||
图片预览





文档简介
课件16张PPT。4.3 空间直角坐标系与空间
两点间的距离公式一、空间物体位置的描述问题1:怎样确定你的课室在教学楼中的
位置?
2、怎样在图书馆中查找某本书?答:1、先确定水平位置——左右;
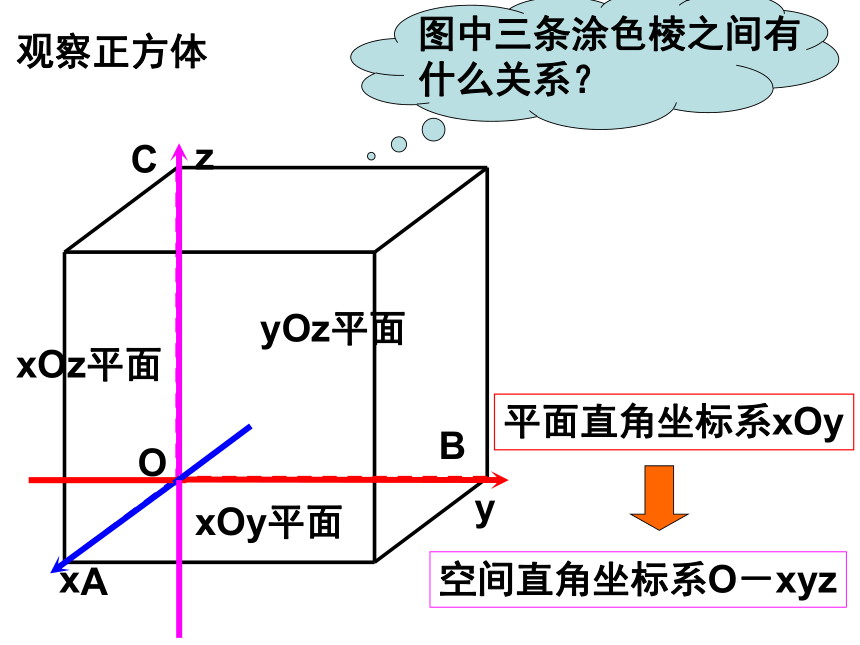
2、再确定竖直位置——上下.确定物体位置仅有平面二维直角坐标系是不够的。要建立空间直角坐标系OABC观察正方体平面直角坐标系xOy空间直角坐标系O-xyzxOy平面yOz平面xOz平面xyz二、空间直角坐标系中点的坐标
空间任意点P的坐标记为(x,y,z)在空间直角坐标系中怎样表示点的坐标?
——可类比平面直角坐标系的方法表示练习:1 、原点O的坐标是( );
2、点P在xoy平面上,则P( );
3、点P在xoz平面上,则P( );
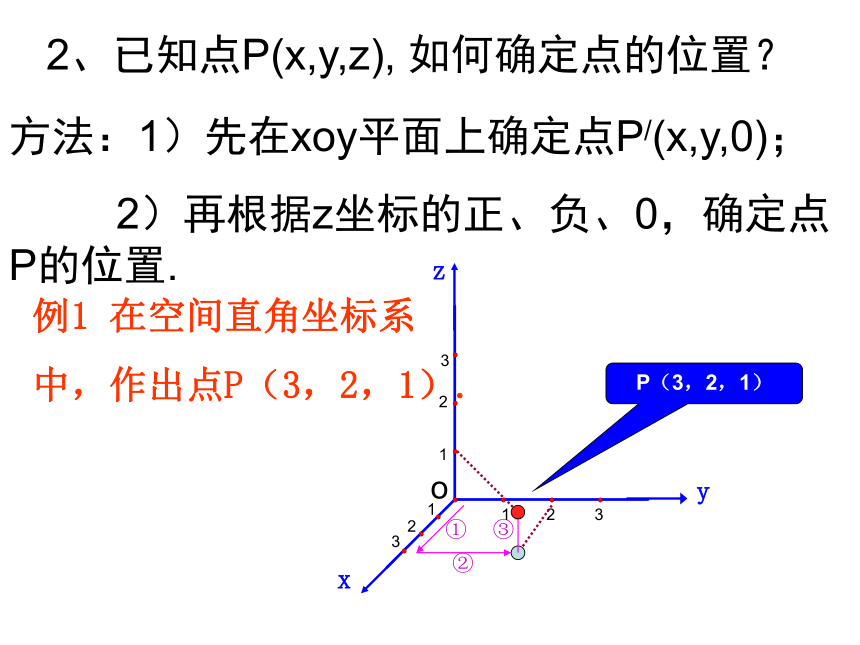
4、点P在yoz平面上,则P( );0,0,0x,y,0x,0,z0,y,z1、确定点的空间坐标5:点P在z轴的上且到原点的距离是3,则P的坐标是___________(0,0,3)或(0,0-3) 规定:点P与z轴的正半轴在xoy平面的异侧时,点P的z坐标与是P到平面xoy的距离的相反数.2、已知点P(x,y,z), 如何确定点的位置?方法:1)先在xoy平面上确定点P/(x,y,0);
2)再根据z坐标的正、负、0,确定点P的位置. 例1 在空间直角坐标系
中,作出点P(3,2,1).③①②P(3,2,1)例2:在空间直角坐标系中画出下列各点
A(0,0,0),B(3,0,0),C(3,2,0),D(0,2,0),A/(0,0,1)B/(3,0,1), C/(3,2,1) ,D/(0,2,1)分析:画出空间直角坐标系,刚好是一个长方体的六个顶点概括:在空间直角坐标系中,空间任意一点P都可以用一个三元有序数组(x,y,z)来表示,反之亦然.
即点与三元有序数组之间建立了一一对应关系练习:如图:正方体棱
长为1,写出各个顶点
的坐标A( )
B( )
C( )
D( )
A/( )
B/( )
C/( )
D/( )1,0,01,1,00,1,00,0,01,0,11,1,10,1,10,0,1练习:在空间直角坐标系中,点M(1,-2,3)1)关于xoy平面的对称点是M/( )2)关于yoz平面的对称点是M/( )3)关于xoz平面的对称点是M/( )4)关于x轴的对称点是M/( )5)关于y轴的对称点是M/( )6)关于z轴的对称点是M/( )1,-2,-3-1,-2,31,2,31,2,-3-1,-2,-3-1,2,37)关于原点的对称点是M/( )-1,2,-3三 空间两点间的距离公式问题1:长方体的对角线是长方体中的那一条线段?
问题2:怎样度量长方体的对角线的长?
问题3:已知长方体的长、宽、高分别是a、
b、c,则对角线的长 问题4:给出空间两点A(x1,y1,z1),P(x2,y2,z2)
可否类比得到一个距离公式?1、设O(0,0,0),P(x0,y0,z0)
则2、空间任意两点A(x1,y1,z1),P(x2,y2,z2)作长方体使A、P为其对角线的顶点
由已知得:C(x2,y1,z1),
B(x2,y2 ,z1)即是:空间两点间的距离公式 公式的记忆方法:同名坐标差的平方和的算术根练2:给定空间直角坐标系,在x轴上找一点P,使它与点P0(4,1,2) 距离为分析:设P(x,0,0),由已知求得x=9或-1(9,0,0)或(-1,0,0)练1:若P(1,2,-2)和Q(-1,0,-1)的
距离是________3小结:1、会画空间直角坐标系;
2、已知点写出其空间直角坐标;
3、空间直角坐标系中距离公式.练习:在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小略解:设M(x,1-x,0),利用距离公式构造出一个二次函数后求最值
位置?
2、怎样在图书馆中查找某本书?答:1、先确定水平位置——左右;
2、再确定竖直位置——上下.确定物体位置仅有平面二维直角坐标系是不够的。要建立空间直角坐标系OABC观察正方体平面直角坐标系xOy空间直角坐标系O-xyzxOy平面yOz平面xOz平面xyz二、空间直角坐标系中点的坐标
空间任意点P的坐标记为(x,y,z)在空间直角坐标系中怎样表示点的坐标?
——可类比平面直角坐标系的方法表示练习:1 、原点O的坐标是( );
2、点P在xoy平面上,则P( );
3、点P在xoz平面上,则P( );
4、点P在yoz平面上,则P( );0,0,0x,y,0x,0,z0,y,z1、确定点的空间坐标5:点P在z轴的上且到原点的距离是3,则P的坐标是___________(0,0,3)或(0,0-3) 规定:点P与z轴的正半轴在xoy平面的异侧时,点P的z坐标与是P到平面xoy的距离的相反数.2、已知点P(x,y,z), 如何确定点的位置?方法:1)先在xoy平面上确定点P/(x,y,0);
2)再根据z坐标的正、负、0,确定点P的位置. 例1 在空间直角坐标系
中,作出点P(3,2,1).③①②P(3,2,1)例2:在空间直角坐标系中画出下列各点
A(0,0,0),B(3,0,0),C(3,2,0),D(0,2,0),A/(0,0,1)B/(3,0,1), C/(3,2,1) ,D/(0,2,1)分析:画出空间直角坐标系,刚好是一个长方体的六个顶点概括:在空间直角坐标系中,空间任意一点P都可以用一个三元有序数组(x,y,z)来表示,反之亦然.
即点与三元有序数组之间建立了一一对应关系练习:如图:正方体棱
长为1,写出各个顶点
的坐标A( )
B( )
C( )
D( )
A/( )
B/( )
C/( )
D/( )1,0,01,1,00,1,00,0,01,0,11,1,10,1,10,0,1练习:在空间直角坐标系中,点M(1,-2,3)1)关于xoy平面的对称点是M/( )2)关于yoz平面的对称点是M/( )3)关于xoz平面的对称点是M/( )4)关于x轴的对称点是M/( )5)关于y轴的对称点是M/( )6)关于z轴的对称点是M/( )1,-2,-3-1,-2,31,2,31,2,-3-1,-2,-3-1,2,37)关于原点的对称点是M/( )-1,2,-3三 空间两点间的距离公式问题1:长方体的对角线是长方体中的那一条线段?
问题2:怎样度量长方体的对角线的长?
问题3:已知长方体的长、宽、高分别是a、
b、c,则对角线的长 问题4:给出空间两点A(x1,y1,z1),P(x2,y2,z2)
可否类比得到一个距离公式?1、设O(0,0,0),P(x0,y0,z0)
则2、空间任意两点A(x1,y1,z1),P(x2,y2,z2)作长方体使A、P为其对角线的顶点
由已知得:C(x2,y1,z1),
B(x2,y2 ,z1)即是:空间两点间的距离公式 公式的记忆方法:同名坐标差的平方和的算术根练2:给定空间直角坐标系,在x轴上找一点P,使它与点P0(4,1,2) 距离为分析:设P(x,0,0),由已知求得x=9或-1(9,0,0)或(-1,0,0)练1:若P(1,2,-2)和Q(-1,0,-1)的
距离是________3小结:1、会画空间直角坐标系;
2、已知点写出其空间直角坐标;
3、空间直角坐标系中距离公式.练习:在xoy平面内的直线x+y=1上确定一点M,使M到N(6,5,1)的距离最小略解:设M(x,1-x,0),利用距离公式构造出一个二次函数后求最值
