1.3 正方形的性质与判定(第1课时) 课件(共39张PPT)
文档属性
| 名称 | 1.3 正方形的性质与判定(第1课时) 课件(共39张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 11:08:08 | ||
图片预览







文档简介
(共39张PPT)
九上数学同步精品课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第一章 特殊平行四边形
1.3 正方形的性质与判定(第1课时)
精品教学课件
1. 探索并证明正方形的性质,并了解平行四边形、
矩形、菱形之间的联系和区别;(重点、难点)
2.探索并证明正方形的判定,并了解平行四边形、
矩形、菱形之间的联系和区别;(重点、难点)
3.会运用正方形的性质及判定条件进行有关的论证
和计算 . (难点)
学习目标
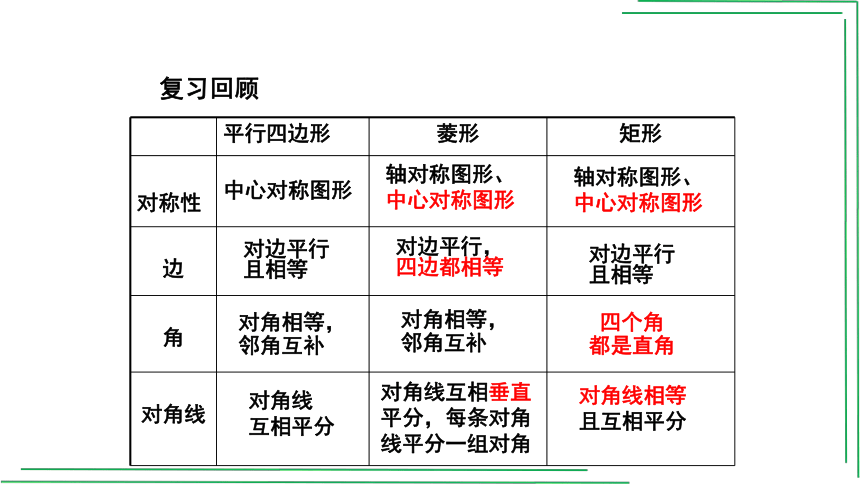
平行四边形 菱形 矩形
对称性
边
角
对角线
复习回顾
中心对称图形
轴对称图形、中心对称图形
轴对称图形、中心对称图形
对边平行
且相等
对边平行
且相等
对边平行,
四边都相等
对角相等,
邻角互补
对角相等,
邻角互补
四个角
都是直角
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
复习回顾
平行四边形、菱形、矩形之间的关系:
平行四边形
菱形
矩形
思考一下:是否有一种四边形既是菱形又是矩形呢?
?
导入新课
活动:观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
讲授新课
矩 形
〃
〃
活动1:矩形怎样变化后就成了正方形呢 你有什么
发现?
问题引入
知识点一 正方形的性质
正方形
活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.
问题2:经过变化后得到特殊四边形是什么四边形?
有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
正方形
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
归纳总结
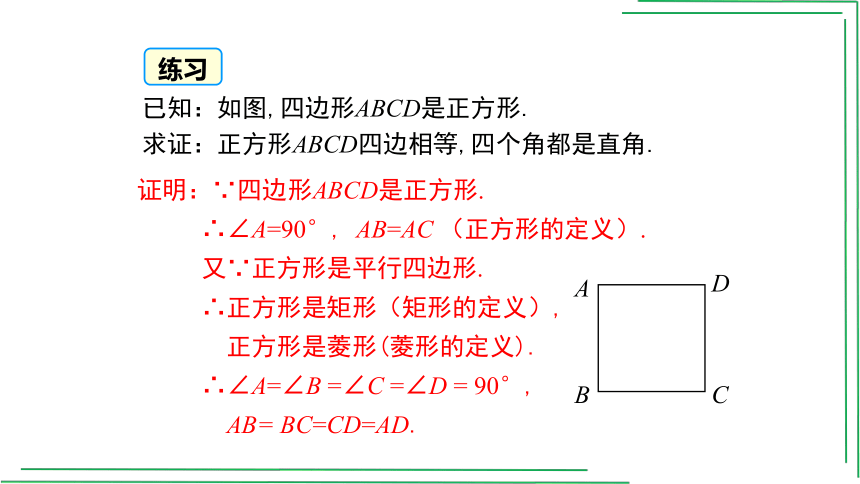
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
练习
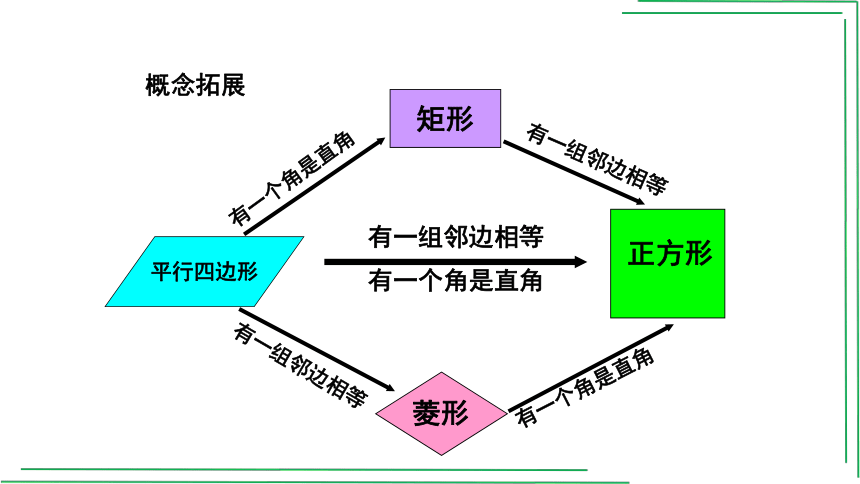
概念拓展
平行四边形
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
有一个角是直角
有一组邻边相等
知识点二 正方形的性质探究和证明
A
B
C
D
填一填:
角:
边:
对角线:
对称性:
四个角都是直角.
四条边相等.
对角线相等且互相垂直平分.
a
a
a
a
轴对称图形(4条对称轴).
1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
定理
提示:可以先通过证明来得到正方形是矩形、菱形,然后利用矩形和菱形的定理来完成该题.
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
想一想: 正方形是矩形吗?是菱形吗?
矩形
菱形
正方形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以平行四边形、矩形、菱形有的性质,正方形都有.
归纳
归纳结论
正方形
对角线
边
边
对角线
对角线
角
对边平行且相等
相互平分
相等
四个角相等都是90°
相互垂直且
平分对角
四边相等
对称性
轴对称图形(4条对称轴)
例1:如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.
知识点三 正方形性质定理的应用
典例精析
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
(正方形的四条边都相等,四个角都是直角)
∴∠DCF=180°-∠BCE=180°-90°=90°.
A
B
D
C
F
E
A
B
D
F
E
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
(2)延长BE交DE于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°.∴∠CBE+∠F=90° , ∴∠BMF=90°.
∴BE⊥DF.
C
M
例2:如图,已知四边形ABCD是正方形,对角线AC与BD相交于点O , MN∥AB ,且分别于OA , OB相交于点M , N.
求证:(1)BM = CN;(2)BM⊥CN.
A
B
C
D
O
M
N
证明:(1)∵MN∥AB.
∴∠1 =∠2 =∠3 =∠4 = 45°.
∴OM = ON.
∵OA= OB,
∴OA- OM = OB - ON,AM=BN.
又∵∠2=∠NBC,AB=BC.
∴△ABM ≌△BCN(SAS) ∴BM=CN.
1
2
3
4
A
B
C
D
O
M
N
(2)延长CN交线段MB于点Q.
∵△ABM≌△BCN.
∴∠6=∠8.
∵∠OCB =∠ABO =45°.
∴∠5=∠7.
又∵∠ONC=∠QNB.
∴180°-∠5 -∠ONC = 180°-∠7 -∠QNB,
∠CON =∠NQB = 90°.
∴BM⊥CN.
Q
5
7
6
8
当堂练习
1、如图,正方形ABCD中,AF=BE, AF与BE相交于点O,
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
D
A
C
B
F
E
证明:(1)∵四边形ABCD是正方形.
∴AD=AB,∠DAB=∠ABC =90° .
又∵ AF=BE
∴ △DAF≌△ABE(SAS).
证明:(2)∵ △DAF≌△ABE
∴ ∠ADF=∠BAE
∵ ∠DAB =90° .
∴ ∠ADF+ AFD= 90°
∴ ∠BAE + AFD= 90°
∴DF ⊥AE
∴ ∠AOE= 90°
2、如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°.
而F是CB的延长线上的点,
∴∠ABF=90°.
在△ADE和△ABF中,
AB=AD,∠ABF=∠ADE,BF=DE,
∴△ADE≌△ABF(SAS).
如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(2)若BC=8,DE=6,求△AEF的面积.
(2)解:∵BC=8,∴AD=8.
在Rt△ADE中,∴AE = =10.
∵ △ADE≌△ABF
∴AE=AF, ∠FAB= ∠EAD,
∠EAF= ∠FAB + ∠BAE = ∠EAD +∠BAE =90°.
∴S△AEF的面积=1/2AE2=1/2×100=50.
3.如图,正方形AEFG的顶点E,G分别在正方形ABCD的边AB,AD上,连接BF,DF.
求证:BF=DF.
证明:∵四边形ABCD和AEFG都是正方形,
∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°.
∵BE=AB-AE,DG=AD-AG,
∴BE=DG.
在△BEF和△DGF中,
BE=DG,∠BEF=∠DGF,EF=GF,
∴△BEF≌△DGF(SAS).
∴BF=DF.
4.已知:如图,在正方形ABCD中,点F在CD上,
AE平分∠BAF,E为BC的中点.
求证:AF=BE+DF.
证明:将△ABE逆时针旋转90°
则AB=AD,BE=DE′,
∠E′AE=90°,
∠ADE′=∠ABE=90°.
∴E′,D,F三点共线.
∵AE是∠BAF的角平分线,
∴∠1=∠2.
又∵四边形ABCD是正方形,
∴∠B=90°.
∴∠AEB=∠E′=90°-∠1=90°-∠2=∠E′AF.
∴AF=FE′=FD+DE′=FD+BE.
5.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=( -1)cm,
∴BE=( -1)cm.
课后作业
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
2.正方形具有而菱形不一定具有的性质( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
B
D
3、求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
4、如图,在正方形ABCD中, ΔBEC是等边三角形,
求证: ∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
5、四边形ABCD是正方形,以正方形ABCD的一边作等边△ADE,求∠BEC的大小.
解:当等边△ADE在正方形ABCD外部时,如图①,AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
6、如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
(1)求证:△APB≌△DPC;
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,
∴AP=DP.
又∵AP=AB=AD,
∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°.
∴∠PAC=∠DAP-∠DAC=15°.
∴∠BAP=∠BAC-∠PAC=30°.
∴∠BAP=2∠PAC.
(2)求证:∠BAP=2∠PAC.
7、如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC , PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步精品课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第一章 特殊平行四边形
1.3 正方形的性质与判定(第1课时)
精品教学课件
1. 探索并证明正方形的性质,并了解平行四边形、
矩形、菱形之间的联系和区别;(重点、难点)
2.探索并证明正方形的判定,并了解平行四边形、
矩形、菱形之间的联系和区别;(重点、难点)
3.会运用正方形的性质及判定条件进行有关的论证
和计算 . (难点)
学习目标
平行四边形 菱形 矩形
对称性
边
角
对角线
复习回顾
中心对称图形
轴对称图形、中心对称图形
轴对称图形、中心对称图形
对边平行
且相等
对边平行
且相等
对边平行,
四边都相等
对角相等,
邻角互补
对角相等,
邻角互补
四个角
都是直角
对角线
互相平分
对角线相等
且互相平分
对角线互相垂直平分,每条对角线平分一组对角
复习回顾
平行四边形、菱形、矩形之间的关系:
平行四边形
菱形
矩形
思考一下:是否有一种四边形既是菱形又是矩形呢?
?
导入新课
活动:观察下面图形,正方形是我们熟悉的几何图形,在生活中无处不在.
你还能举出其他的例子吗?
讲授新课
矩 形
〃
〃
活动1:矩形怎样变化后就成了正方形呢 你有什么
发现?
问题引入
知识点一 正方形的性质
正方形
活动2:把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.
问题2:经过变化后得到特殊四边形是什么四边形?
有一组邻边相等,并且有一个角是直角的平行四边形是正方形.
正方形
邻边相等
矩形
〃
〃
正方形
〃
〃
菱 形
一个角是直角
正方形
∟
正方形定义:
有一组邻边相等并且有一个角是直角的平行四边形叫正方形.
归纳总结
已知:如图,四边形ABCD是正方形.
求证:正方形ABCD四边相等,四个角都是直角.
A
B
C
D
证明:∵四边形ABCD是正方形.
∴∠A=90°, AB=AC (正方形的定义).
又∵正方形是平行四边形.
∴正方形是矩形(矩形的定义),
正方形是菱形(菱形的定义).
∴∠A=∠B =∠C =∠D = 90°,
AB= BC=CD=AD.
练习
概念拓展
平行四边形
正方形
矩形
有一组邻边相等
菱形
有一个角是直角
有一组邻边相等
有一个角是直角
有一个角是直角
有一组邻边相等
知识点二 正方形的性质探究和证明
A
B
C
D
填一填:
角:
边:
对角线:
对称性:
四个角都是直角.
四条边相等.
对角线相等且互相垂直平分.
a
a
a
a
轴对称图形(4条对称轴).
1.正方形的四个角都是直角,四条边相等.
2.正方形的对角线相等且互相垂直平分.
定理
提示:可以先通过证明来得到正方形是矩形、菱形,然后利用矩形和菱形的定理来完成该题.
已知:如图,四边形ABCD是正方形.对角线AC、BD相交于点O.求证:AO=BO=CO=DO,AC⊥BD.
A
B
C
D
O
证明:∵正方形ABCD是矩形,
∴AO=BO=CO=DO.
∵正方形ABCD是菱形.
∴AC⊥BD.
想一想: 正方形是矩形吗?是菱形吗?
矩形
菱形
正方形
平行四边形
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所以平行四边形、矩形、菱形有的性质,正方形都有.
归纳
归纳结论
正方形
对角线
边
边
对角线
对角线
角
对边平行且相等
相互平分
相等
四个角相等都是90°
相互垂直且
平分对角
四边相等
对称性
轴对称图形(4条对称轴)
例1:如图在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF. BE与DF之间有怎样的关系?请说明理由.
知识点三 正方形性质定理的应用
典例精析
解:BE=DF,且BE⊥DF.理由如下:
(1)∵四边形ABCD是正方形.
∴BC=DC,∠BCE =90° .
(正方形的四条边都相等,四个角都是直角)
∴∠DCF=180°-∠BCE=180°-90°=90°.
A
B
D
C
F
E
A
B
D
F
E
∴∠BCE=∠DCF.
又∵CE=CF.
∴△BCE≌△DCF.
∴BE=DF.
(2)延长BE交DE于点M,
∵△BCE≌△DCF ,
∴∠CBE =∠CDF.
∵∠DCF =90° ,
∴∠CDF +∠F =90°.∴∠CBE+∠F=90° , ∴∠BMF=90°.
∴BE⊥DF.
C
M
例2:如图,已知四边形ABCD是正方形,对角线AC与BD相交于点O , MN∥AB ,且分别于OA , OB相交于点M , N.
求证:(1)BM = CN;(2)BM⊥CN.
A
B
C
D
O
M
N
证明:(1)∵MN∥AB.
∴∠1 =∠2 =∠3 =∠4 = 45°.
∴OM = ON.
∵OA= OB,
∴OA- OM = OB - ON,AM=BN.
又∵∠2=∠NBC,AB=BC.
∴△ABM ≌△BCN(SAS) ∴BM=CN.
1
2
3
4
A
B
C
D
O
M
N
(2)延长CN交线段MB于点Q.
∵△ABM≌△BCN.
∴∠6=∠8.
∵∠OCB =∠ABO =45°.
∴∠5=∠7.
又∵∠ONC=∠QNB.
∴180°-∠5 -∠ONC = 180°-∠7 -∠QNB,
∠CON =∠NQB = 90°.
∴BM⊥CN.
Q
5
7
6
8
当堂练习
1、如图,正方形ABCD中,AF=BE, AF与BE相交于点O,
(1)求证:△DAF≌△ABE;
(2)求∠AOD的度数;
D
A
C
B
F
E
证明:(1)∵四边形ABCD是正方形.
∴AD=AB,∠DAB=∠ABC =90° .
又∵ AF=BE
∴ △DAF≌△ABE(SAS).
证明:(2)∵ △DAF≌△ABE
∴ ∠ADF=∠BAE
∵ ∠DAB =90° .
∴ ∠ADF+ AFD= 90°
∴ ∠BAE + AFD= 90°
∴DF ⊥AE
∴ ∠AOE= 90°
2、如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(1)求证:△ADE≌△ABF;
(1)证明:∵四边形ABCD是正方形,
∴AD=AB,∠D=∠ABC=90°.
而F是CB的延长线上的点,
∴∠ABF=90°.
在△ADE和△ABF中,
AB=AD,∠ABF=∠ADE,BF=DE,
∴△ADE≌△ABF(SAS).
如图,四边形ABCD是正方形,E,F分别是DC和CB的延长线上的点,且DE=BF,连接AE,AF,EF.
(2)若BC=8,DE=6,求△AEF的面积.
(2)解:∵BC=8,∴AD=8.
在Rt△ADE中,∴AE = =10.
∵ △ADE≌△ABF
∴AE=AF, ∠FAB= ∠EAD,
∠EAF= ∠FAB + ∠BAE = ∠EAD +∠BAE =90°.
∴S△AEF的面积=1/2AE2=1/2×100=50.
3.如图,正方形AEFG的顶点E,G分别在正方形ABCD的边AB,AD上,连接BF,DF.
求证:BF=DF.
证明:∵四边形ABCD和AEFG都是正方形,
∴AB=AD,AE=AG=EF=FG,∠BEF=∠DGF=90°.
∵BE=AB-AE,DG=AD-AG,
∴BE=DG.
在△BEF和△DGF中,
BE=DG,∠BEF=∠DGF,EF=GF,
∴△BEF≌△DGF(SAS).
∴BF=DF.
4.已知:如图,在正方形ABCD中,点F在CD上,
AE平分∠BAF,E为BC的中点.
求证:AF=BE+DF.
证明:将△ABE逆时针旋转90°
则AB=AD,BE=DE′,
∠E′AE=90°,
∠ADE′=∠ABE=90°.
∴E′,D,F三点共线.
∵AE是∠BAF的角平分线,
∴∠1=∠2.
又∵四边形ABCD是正方形,
∴∠B=90°.
∴∠AEB=∠E′=90°-∠1=90°-∠2=∠E′AF.
∴AF=FE′=FD+DE′=FD+BE.
5.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=( -1)cm,
∴BE=( -1)cm.
课后作业
1.正方形具有而矩形不一定具有的性质是 ( )
A.四个角相等
B.对角线互相垂直平分
C.对角互补
D.对角线相等
2.正方形具有而菱形不一定具有的性质( )
A.四条边相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.对角线相等
B
D
3、求证: 正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
A
D
C
B
O
已知: 如图,四边形ABCD是正方形,对角线AC、BD相
交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的
等腰直角三角形.
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都
是等腰直角三角形,并且
△ABO≌ △BCO ≌ △CDO ≌ △DAO.
4、如图,在正方形ABCD中, ΔBEC是等边三角形,
求证: ∠EAD=∠EDA=15° .
证明:∵ ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵ 四边形ABCD是正方形,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴AB=BE=CE=CD, ∠ABE= ∠DCE=30°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE= ∠BEA= ∠CDE= ∠CED=75°,
∴∠EAD= ∠EDA=90°-75°=15°.
5、四边形ABCD是正方形,以正方形ABCD的一边作等边△ADE,求∠BEC的大小.
解:当等边△ADE在正方形ABCD外部时,如图①,AB=AE,∠BAE=90°+60°=150°.
∴∠AEB=15°.
同理可得∠DEC=15°.
∴∠BEC=60°-15°-15°=30°;
当等边△ADE在正方形ABCD内部时,如图②,
AB=AE,∠BAE=90°-60°=30°,
∴∠AEB=75°.
同理可得∠DEC=75°.
∴∠BEC=360°-75°-75°-60°=150°.
综上所述,∠BEC的大小为30°或150°.
6、如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD.
(1)求证:△APB≌△DPC;
解:∵四边形ABCD是正方形,
∴∠ABC=∠DCB=90°.
∵PB=PC,
∴∠PBC=∠PCB.
∴∠ABC-∠PBC=∠DCB-∠PCB,
即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,
∴AP=DP.
又∵AP=AB=AD,
∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°.
∴∠PAC=∠DAP-∠DAC=15°.
∴∠BAP=∠BAC-∠PAC=30°.
∴∠BAP=2∠PAC.
(2)求证:∠BAP=2∠PAC.
7、如图,在正方形ABCD中,P为BD上一点,PE⊥BC于E, PF⊥DC于F.试说明:AP=EF.
A
B
C
D
P
E
F
解:
连接PC,AC.
又∵PE⊥BC , PF⊥DC,
∵四边形ABCD是正方形,
∴∠FCE=90°, AC垂直平分BD,
∴四边形PECF是矩形,
∴PC=EF.
∴AP=PC.
∴AP=EF.
1.四个角都是直角
2.四条边都相等
3.对角线相等且互相垂直平分
正方形
性质
定义
有一组邻相等,并且有一个角是直角的平行四边形叫做正方形
课堂小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
