1.3 正方形的性质与判定(第2课时) 课件(共40张ppt)
文档属性
| 名称 | 1.3 正方形的性质与判定(第2课时) 课件(共40张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-24 11:08:08 | ||
图片预览






文档简介
(共40张PPT)
九上数学同步精品课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第一章 特殊平行四边形
1.3 正方形的性质与判定(第2课时)
精品教学课件
1、学会正方形的判定,掌握判定方法;(重点)
2、运用正方形的判定方法进行几何图形的证明与应用 .(难点)
学习目标
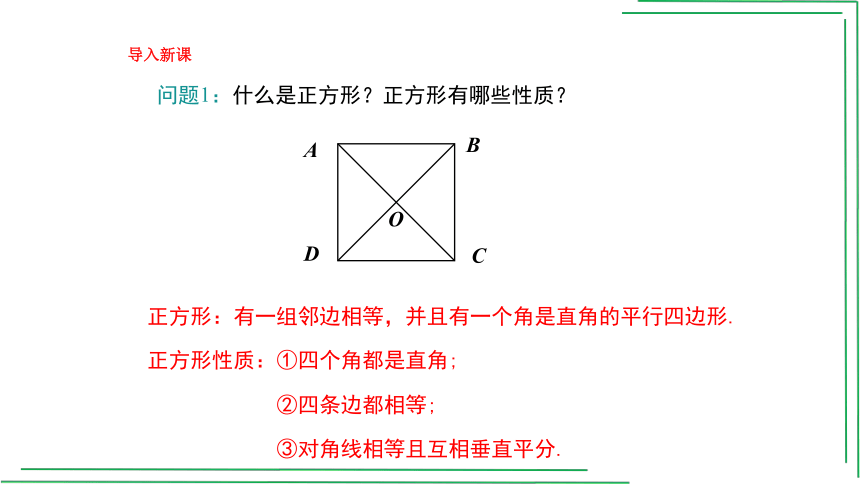
问题1:什么是正方形?正方形有哪些性质?
A
B
C
D
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
O
导入新课
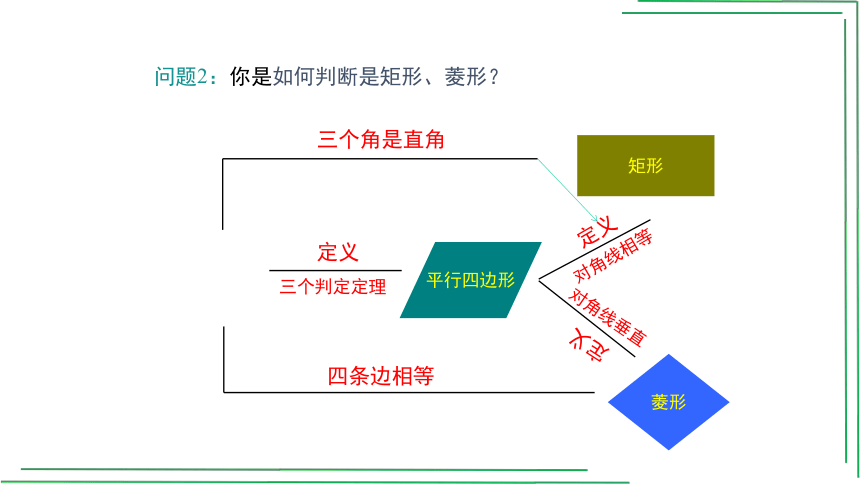
问题2:你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
三个角是直角
四条边相等
定义
三个判定定理
定义
对角线相等
定义
对角线垂直
知识点一 正方形判定的定理
讲授新课
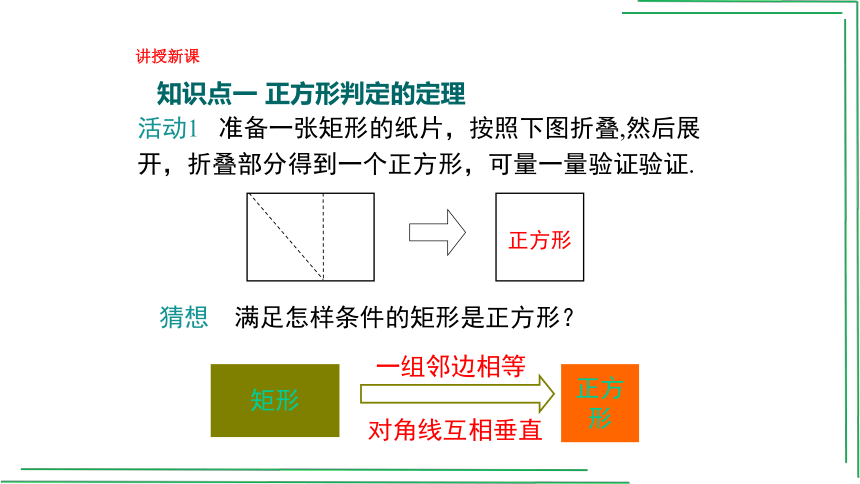
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?
(1)
(2)
(3)
(4)
菱形
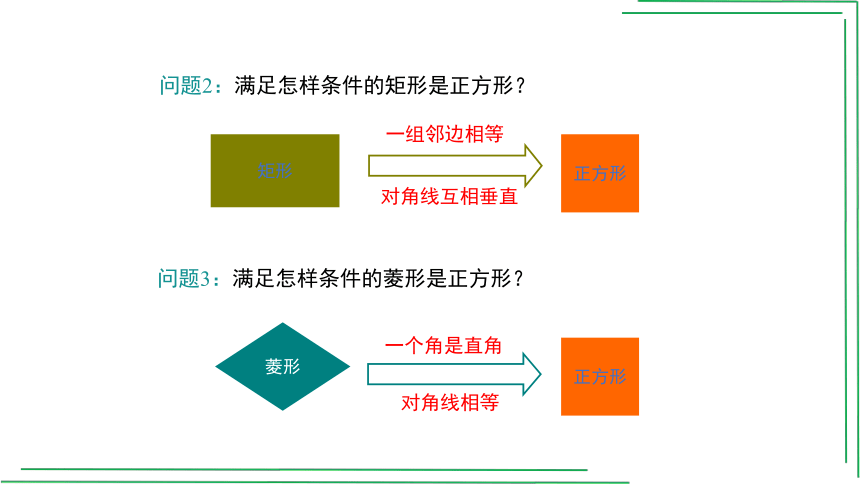
问题2:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
问题3:满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
练习
A
B
C
D
O
对角线互相垂直的矩形是正方形.
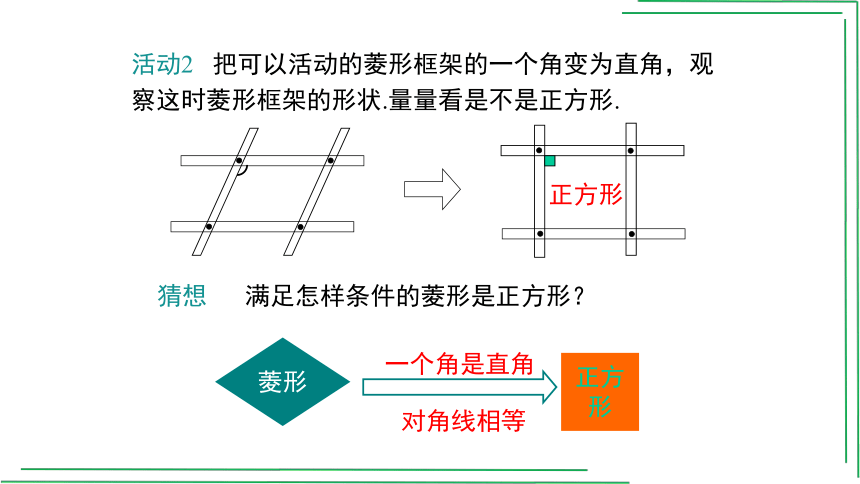
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
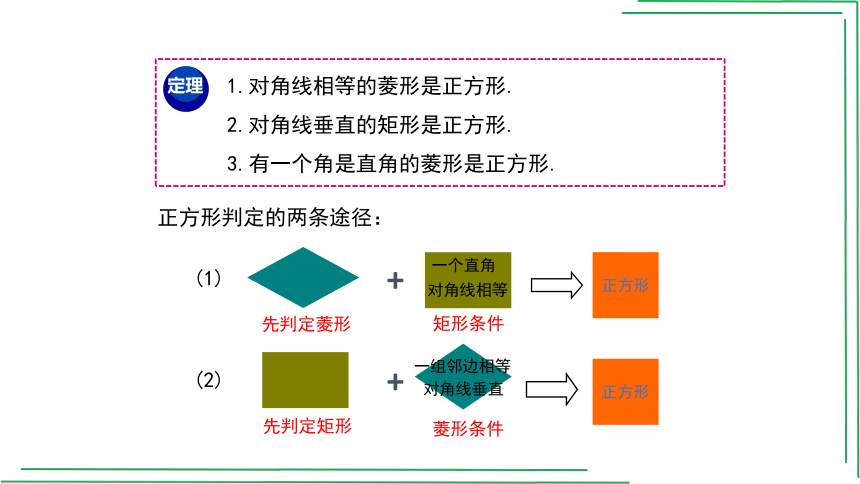
1.对角线相等的菱形是正方形.
2.对角线垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
定理
正方形判定的两条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件
菱形条件
(1)
(2)
一个直角
对角线相等
一组邻边相等
对角线垂直
例1:如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.
知识点二 正方形判定定理的应用
典例精析
F
A
B
E
C
D
解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形;
45°
45°
F
A
B
E
C
D
证明: ∵ BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.
例2:已知:如图所示,在Rt△ABC中, ∠C=90° , ∠BAC , ∠ABC的平分线于点D , DE⊥BC于点E , DF⊥AC于点F.
求证:四边形CEDF是正方形.
证明: 如图所示,过点D作DG⊥AB于点G.
∵DF⊥AC , DE⊥BC ,
∴∠DFC=∠DEC=90°.
又∠C=90°,
∴四边形CEDF是矩形 (有三个角是直角的四边形是矩形).
∴AD平分∠BAC , DF⊥AC , DG⊥AB.
∴DF=DG. 同理可得 DE=DG , ∴DE=DF.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
C
E
B
A
F
D
G
例3:如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
B
O
E
H
G
F
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
平行四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
平行四边形
矩形
菱形
正方形
等腰梯形
直角梯形
梯形
原四边形可以是:
知识点三 中点四边形
特殊四边形的中点四边形:
平行四边形的中点四边形是平行四边形
菱形的中点四边形是矩形
矩形的中点四边形是菱形
正方形的中点四边形是正方形
等腰梯形的中点四边形是菱形
直角梯形的中点四边形是平行四边形
梯形的中点四边形是平行四边形
特殊四边形的中点四边形:
对角线垂直的四边形的中点四边形是矩形
对角线相等的四边形的中点四边形是菱形
对角线既相等又垂直的四边形的中点四边形是正方形
对角线既不相等又不垂直的四边形的中点四边形是平行四边形
总结归纳
一般四边形的中点四边形:
决定中点四边形EFGH的形状的主要因素是原四边形ABCD的对角线的长度和位置关系
原四边形对角线关系 不相等、不垂直 相等 垂直 相等且垂直
所得中点四边形形状
平行四边形
菱形
矩形
正方形
当堂练习
2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
3.在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
A
D
B
C
O
A
D
B
C
O
E
45°
90°
22.5°
第3题图
第4题图
45°
5.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=( -1)cm,
∴BE=( -1)cm.
6.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(1) 求证: ADB= CDB;
(2) 若 ADC=90 ,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明(1)∵BD平分∠ABC,∴∠1=∠2.
∵AB = BC,BD=BD,
∴△ABD≌△CBD (SAS).
∴∠ADB=∠CDB.
1
2
C
A
B
D
P
M
N
(2)∵∠ADC=90°,
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
7.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
①试说明四边形AEDF的形状,并说明理由.
②连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
解:①∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
②∵四边形AEDF为菱形,
∴AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
③在②的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
解:由四边形AEDF为正方形
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
课后作业
1.四个内角都相等的四边形一定是( )
A.正方形 B.菱形
C.矩形 D.平行四边形
C
2. 如图,已知四边形ABCD是平行四边形,下列结论不正确的是( )
A. 当AB=BC时,它是菱形
B. 当∠ABC=90°时,它是矩形
C. 当AC⊥BD时,它是菱形
D. 当AC=BD时,它是正方形
D
3.如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
AB∥DC B. AC=BD
C. AC⊥BD D. AB=DC
C
4. 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
A. -4+4
B. 4 +4
C. 8-4
D. +1
A
5.如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
求证:四边形ABCD是正方形.
证明:由题意,得∠BAE=∠EAG,
∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°.
∴四边形ABCD是矩形.
∵AB=AG,AD=AG,
∴AB=AD.
∴四边形ABCD是正方形.
6.如图,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
证明:(1)如图,连接GE,
∵AB∥CD,∴∠AEG=∠CGE.
∵GF∥HE,∴∠HEG=∠FGE.
∴∠HEA=∠CGF.
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°.
∵四边形EFGH是菱形,
∴HG=HE.在Rt△HAE和Rt△GDH中,
AH=DG,HE=HG,
∴Rt△HAE≌Rt△GDH(HL).
∴∠AHE=∠DGH.
又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°.∴∠GHE=90°.
∴菱形EFGH为正方形.
课堂小结
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
九上数学同步精品课件
北师大版九年级上册
北师大版九年级上册数学教学课件
第一章 特殊平行四边形
1.3 正方形的性质与判定(第2课时)
精品教学课件
1、学会正方形的判定,掌握判定方法;(重点)
2、运用正方形的判定方法进行几何图形的证明与应用 .(难点)
学习目标
问题1:什么是正方形?正方形有哪些性质?
A
B
C
D
正方形:有一组邻边相等,并且有一个角是直角的平行四边形.
正方形性质:①四个角都是直角;
②四条边都相等;
③对角线相等且互相垂直平分.
O
导入新课
问题2:你是如何判断是矩形、菱形?
平行四边形
矩形
菱形
三个角是直角
四条边相等
定义
三个判定定理
定义
对角线相等
定义
对角线垂直
知识点一 正方形判定的定理
讲授新课
活动1 准备一张矩形的纸片,按照下图折叠,然后展开,折叠部分得到一个正方形,可量一量验证验证.
正方形
猜想 满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
想一想:将矩形纸片对折两次,怎样裁剪才能使剪下的三角形
展开后是个正方形?
(1)
(2)
(3)
(4)
菱形
问题2:满足怎样条件的矩形是正方形?
矩形
正方形
一组邻边相等
对角线互相垂直
问题3:满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在矩形ABCD中,AC , DB是它的两条对角线,
AC⊥DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是矩形,
∴ AO=CO=BO=DO ,∠ADC=90°.
∵AC⊥DB,
∴ AD=AB=BC=CD,
∴四边形ABCD是正方形.
练习
A
B
C
D
O
对角线互相垂直的矩形是正方形.
活动2 把可以活动的菱形框架的一个角变为直角,观察这时菱形框架的形状.量量看是不是正方形.
正方形
菱形
猜想 满足怎样条件的菱形是正方形?
正方形
一个角是直角
对角线相等
已知:如图,在菱形ABCD中,AC , DB是它的两条对角线,
AC=DB.
求证:四边形ABCD是正方形.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥DB.
∵AC=DB,
∴ AO=BO=CO=DO,
∴△AOD,△AOB,△COD,△BOC是等腰直角三角形,
∴∠DAB=∠ABC=∠BCD=∠ADC=90°,
∴四边形ABCD是正方形.
证一证
A
B
C
D
O
对角线相等的菱形是正方形.
1.对角线相等的菱形是正方形.
2.对角线垂直的矩形是正方形.
3.有一个角是直角的菱形是正方形.
定理
正方形判定的两条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件
菱形条件
(1)
(2)
一个直角
对角线相等
一组邻边相等
对角线垂直
例1:如图,在矩形ABCD中, BE平分∠ABC , CE平分∠DCB , BF∥CE , CF∥BE.
求证:四边形BECF是正方形.
知识点二 正方形判定定理的应用
典例精析
F
A
B
E
C
D
解析:先由两组平行线得出四边形BECF平行四边形;再由一个直角,得出是矩形;最后由一组邻边相等可得正方形;
45°
45°
F
A
B
E
C
D
证明: ∵ BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD是矩形,
∴ ∠ABC = 90°, ∠DCB = 90°,
∵BE平分∠ABC, CE平分∠ DCB,
∴∠EBC = 45°, ∠ECB = 45°,
∴ ∠ EBC =∠ ECB .
∴ EB=EC,∴□ BECF是菱形 .
在△EBC中
∵ ∠EBC = 45°,∠ECB = 45°,
∴∠BEC = 90°,
∴菱形BECF是正方形.
例2:已知:如图所示,在Rt△ABC中, ∠C=90° , ∠BAC , ∠ABC的平分线于点D , DE⊥BC于点E , DF⊥AC于点F.
求证:四边形CEDF是正方形.
证明: 如图所示,过点D作DG⊥AB于点G.
∵DF⊥AC , DE⊥BC ,
∴∠DFC=∠DEC=90°.
又∠C=90°,
∴四边形CEDF是矩形 (有三个角是直角的四边形是矩形).
∴AD平分∠BAC , DF⊥AC , DG⊥AB.
∴DF=DG. 同理可得 DE=DG , ∴DE=DF.
∴四边形CEDF是正方形(有一组邻边相等的矩形是正方形).
C
E
B
A
F
D
G
例3:如图,EG,FH过正方形ABCD的对角线的交点O,且EG⊥FH.求证:四边形EFGH是正方形.
证明:∵四边形ABCD为正方形,
∴OB=OC,∠ABO=∠BCO =45°,
∠BOC=90°=∠COH+∠BOH.
∵EG⊥FH,
∴∠BOE+∠BOH=90°,
∴∠COH=∠BOE,
∴△CHO ≌△BEO,∴OE=OH.
同理可证:OE=OF=OG,
B
A
C
B
O
E
H
G
F
∴OE=OF=OG=OH.
又∵EG⊥FH,
∴四边形EFGH为菱形.
∵EO+GO=FO+HO ,即EG=HF,
∴四边形EFGH为正方形.
B
A
C
B
O
E
H
G
F
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.顺次连接矩形、正方形各边中点能得到怎样的特殊平行四边形?
A
B
C
D
A
B
C
D
A
B
C
D
矩形
正方形
任意四边形
平行四边形
菱形
正方形
E
F
G
H
E
F
G
H
E
F
G
H
做一做:顺次连接任意四边形各边中点所得的四边形是平行四边形.如果四边形ABCD变为特殊的四边形,中点四边形EFGH会有怎样的变化呢?
平行四边形
矩形
菱形
正方形
等腰梯形
直角梯形
梯形
原四边形可以是:
知识点三 中点四边形
特殊四边形的中点四边形:
平行四边形的中点四边形是平行四边形
菱形的中点四边形是矩形
矩形的中点四边形是菱形
正方形的中点四边形是正方形
等腰梯形的中点四边形是菱形
直角梯形的中点四边形是平行四边形
梯形的中点四边形是平行四边形
特殊四边形的中点四边形:
对角线垂直的四边形的中点四边形是矩形
对角线相等的四边形的中点四边形是菱形
对角线既相等又垂直的四边形的中点四边形是正方形
对角线既不相等又不垂直的四边形的中点四边形是平行四边形
总结归纳
一般四边形的中点四边形:
决定中点四边形EFGH的形状的主要因素是原四边形ABCD的对角线的长度和位置关系
原四边形对角线关系 不相等、不垂直 相等 垂直 相等且垂直
所得中点四边形形状
平行四边形
菱形
矩形
正方形
当堂练习
2.一个正方形的对角线长为2cm,则它的面积是
( )
A.2cm2 B.4cm2 C.6cm2 D.8cm2
A
1.平行四边形、矩形、菱形、正方形都具有的是( )
A.对角线互相平分
B.对角线互相垂直
C.对角线相等
D.对角线互相垂直且相等
A
3.在正方形ABC中,∠ADB= ,∠DAC= , ∠BOC= .
4.在正方形ABCD中,E是对角线AC上一点,且AE=AB,则∠EBC的度数是 .
A
D
B
C
O
A
D
B
C
O
E
45°
90°
22.5°
第3题图
第4题图
45°
5.如图,正方形ABCD的边长为1cm,AC为对角线,AE平分∠BAC,EF⊥AC,求BE的长.
解:∵四边形ABCD为正方形,
∴∠B=90°,∠ACB=45°,AB=BC=1cm.
∵EF⊥AC,∴∠EFA=∠EFC=90°.
又∵∠ECF=45°,
∴△EFC是等腰直角三角形,∴EF=FC.
∵∠BAE=∠FAE,∠B=∠EFA=90°,AE=AE,
∴△ABE≌△AFE,
∴AB=AF=1cm,BE=EF.
∴FC=BE.
在Rt△ABC中,
∴FC=AC-AF=( -1)cm,
∴BE=( -1)cm.
6.如图,在四边形ABCD中, AB=BC ,对角线BD平分 ABC , P是BD上一点,过点P作PM AD , PN CD ,垂足分别为M、N.
(1) 求证: ADB= CDB;
(2) 若 ADC=90 ,求证:四边形MPND是正方形.
C
A
B
D
P
M
N
证明(1)∵BD平分∠ABC,∴∠1=∠2.
∵AB = BC,BD=BD,
∴△ABD≌△CBD (SAS).
∴∠ADB=∠CDB.
1
2
C
A
B
D
P
M
N
(2)∵∠ADC=90°,
又∵PM⊥AD,PN⊥CD;
∴∠PMD=∠PND=90°.
∴四边形NPMD是矩形.
∵∠ADB=∠CDB;
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是正方形.
7.如图,△ABC中,D是BC上任意一点,DE∥AC,DF∥AB.
①试说明四边形AEDF的形状,并说明理由.
②连接AD,当AD满足什么条件时,四边形AEDF为菱形,为什么?
解:①∵DE∥AC,DF∥AB,
∴四边形AEDF为平行四边形.
②∵四边形AEDF为菱形,
∴AD平分∠BAC,
则AD平分∠BAC时,四边形AEDF为菱形.
③在②的条件下,当△ABC满足什么条件时,四边形AEDF为正方形,不说明理由.
解:由四边形AEDF为正方形
∴∠BAC=90°,
∴△ABC是以BC为斜边的直角三角形即可.
课后作业
1.四个内角都相等的四边形一定是( )
A.正方形 B.菱形
C.矩形 D.平行四边形
C
2. 如图,已知四边形ABCD是平行四边形,下列结论不正确的是( )
A. 当AB=BC时,它是菱形
B. 当∠ABC=90°时,它是矩形
C. 当AC⊥BD时,它是菱形
D. 当AC=BD时,它是正方形
D
3.如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
AB∥DC B. AC=BD
C. AC⊥BD D. AB=DC
C
4. 如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为( )
A. -4+4
B. 4 +4
C. 8-4
D. +1
A
5.如图,在四边形纸片ABCD中,∠B=∠D=90°,点E,F分别在边BC,CD上,将AB,AD分别沿AE,AF折叠,点B,D恰好都和点G重合,∠EAF=45°.
求证:四边形ABCD是正方形.
证明:由题意,得∠BAE=∠EAG,
∠DAF=∠FAG,
∴∠BAD=2∠EAF=90°.
∴四边形ABCD是矩形.
∵AB=AG,AD=AG,
∴AB=AD.
∴四边形ABCD是正方形.
6.如图,菱形EFGH的三个顶点E,G,H分别在正方形ABCD的边AB,CD,DA上,连接CF.
(1)求证:∠HEA=∠CGF;
(2)当AH=DG时,求证:菱形EFGH为正方形.
证明:(1)如图,连接GE,
∵AB∥CD,∴∠AEG=∠CGE.
∵GF∥HE,∴∠HEG=∠FGE.
∴∠HEA=∠CGF.
(2)∵四边形ABCD是正方形,
∴∠D=∠A=90°.
∵四边形EFGH是菱形,
∴HG=HE.在Rt△HAE和Rt△GDH中,
AH=DG,HE=HG,
∴Rt△HAE≌Rt△GDH(HL).
∴∠AHE=∠DGH.
又∠DHG+∠DGH=90°,
∴∠DHG+∠AHE=90°.∴∠GHE=90°.
∴菱形EFGH为正方形.
课堂小结
5种判定方法
三个角是直角
四条边相等
一个角是直角
或对角线相等
一组邻边相等
或对角线垂直
一组邻边相等
或对角线垂直
一个角是直角
或对角线相等
一个角是直角且一组邻边相等
平行四边形、矩形、菱形、正方形的判定小结
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
