10.2事件的相互独立性 学案(Word版无答案)
文档属性
| 名称 | 10.2事件的相互独立性 学案(Word版无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 24.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 00:00:00 | ||
图片预览


文档简介
第十章 概率
10.2事件的相互独立性导学案
教学目标与核心素养
1.理解两事件相互独立的含义;
2.结合古典概型, 利用独立事件、 互斥事件的概率公式, 计算概率, 并能灵活应用
素养目标:
1.体会特殊与一般、 或然与必然、 化归与转化、 分类讨论等数学思想
2.渗透直观想象、 数学抽象、 逻辑推理、 数学运算等核心养
二、知识回顾
1、什么是互斥事件?
2、什么是对立事件?
三、探究新知
试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。
(1)事件A的发生是否影响事件B的概率?
(2)计算试验1中的P(A),P(B),P(AB),你有什么发现?
在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则
样本空间Ω={( , ),( , ),( , ),( , )},包含4 个等可能的样本点。
而A={( , ),( , )},B={( , ),( , )}
所以AB={(1,0)}
由古典概率模型概率计算公式,
得P(A)=P(B)= ,P(AB)= , 于是 P( )=P( )P( )
试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。采用有放回方式从袋中依次任意摸出两球。设A=“第一次摸到球的标号小于3”,B=“第二次摸到球的标号小于3”。
事件A的发生是否影响事件B的概率?
计算试验2中的P(A),P(B),P(AB),你有什么发现?
第一次m 第二次n
1 2 3 4
1 ( , ) ( , ) ( , ) ( , )
2 ( , ) ( , ) ( , ) ( , )
3 ( , ) ( , ) ( , ) ( , )
4 ( , ) ( , ) ( , ) ( , )
在该试验中,样本空间Ω={(m,n)|m,n∈{1,2,3,4}}共16个等可能的样本点
而A={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)}
B={(1,1),(1,2),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2)}
AB={(1,1),(1,2),(2,1),(2,2)}
所以P(A)=P(B)= ,P(AB)= , 于是 P( )=P( )P( )
积事件AB的概率恰好等于事件A、B概率的乘积。
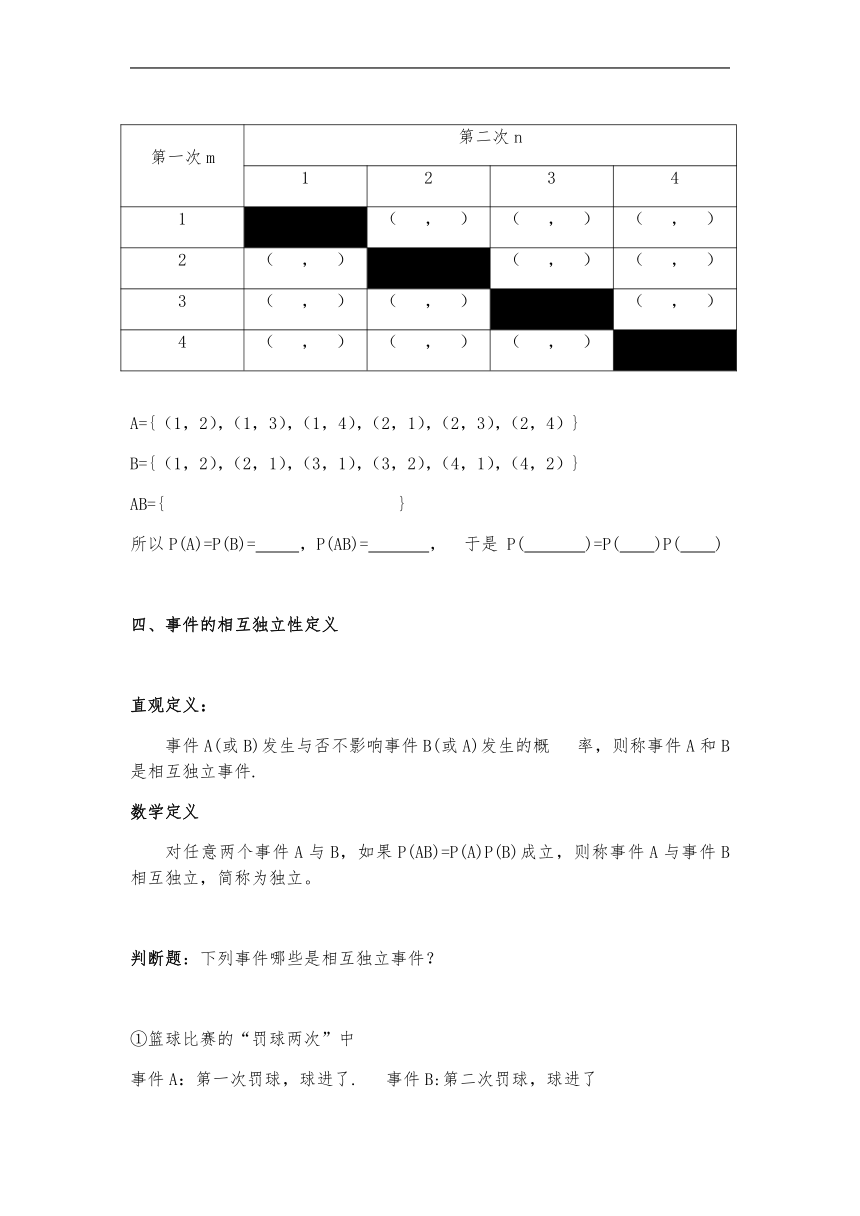
变式:一个袋子中有标号分别为1,2,3,4的4个球,除标号外没有其他差异。采用不放回方式从中任意摸球两次。记事件A=“第一次摸出球的标号小于3”,事件B=“第二次摸出球的标号小于3”,那么事件A与B是否相互独立?
解:因为样本空间Ω={(m,n)|m,n∈{1,2,3,4},且m≠n}共12个等可能的样本点
第一次m 第二次n
1 2 3 4
1 ( , ) ( , ) ( , )
2 ( , ) ( , ) ( , )
3 ( , ) ( , ) ( , )
4 ( , ) ( , ) ( , )
A={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4)}
B={(1,2),(2,1),(3,1),(3,2),(4,1),(4,2)}
AB={ }
所以P(A)=P(B)= ,P(AB)= , 于是 P( )=P( )P( )
四、事件的相互独立性定义
直观定义:
事件A(或B)发生与否不影响事件B(或A)发生的概 率,则称事件A和B是相互独立事件.
数学定义
对任意两个事件A与B,如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立。
判断题:下列事件哪些是相互独立事件?
①篮球比赛的“罚球两次”中
事件A:第一次罚球,球进了. 事件B:第二次罚球,球进了
②抛掷两枚骰子
事件A:第一枚骰子出现偶数点. 事件B:第二枚骰子出现奇数
③袋中有三个红球,两个白球,采取不放回的取球.
事件A:第一次从中任取一个球是白球. 事件B:第二次从中任取一个球是白球.
④袋中有三个红球,两个白球,采取有放回的取球.
事件A:第一次从中任取一个球是白球. 事件B:第二次从中任取一个球是白球.
相互独立事件的性质
若事件A与B相互独立, 则以下三对事件也相互独立: 、 、
必然事件及不可能事件与任何事件A
五、例题解析
例题讲解
例.甲、乙两名射击运动员进行设计比赛,甲的中靶概率为0.8,乙的中靶概率为0.9,求下列事件的概率:
(1)两人都中靶;(2)恰好有一人中靶;
(3)两人都脱靶;(4)至少有一人中靶。
六课堂小结
相互独立事件的定义
相互独立事件的性质
判断两个事件相互独立的方法:①定义法:P(AB)=P(A)P(B)②直接法:由事件本身的性质直接判断两个事件的发生是否相互影响。
趣味小知识
俗话说“三个臭皮匠,顶上一个诸葛亮”.假设三人解决某一问题的概率均为0.5,且相互独立。诸葛亮解决该问题的概率为0.8.你能从数学角度解决这句话的含义吗?
七、目标检测设计
1.袋内有3个白球和2个黑球,从中有放回地摸球,用A表示“第一次摸到白球”,如果“第二次摸到白球”记为B,否则记为C,那么事件A与B,A与C的关系是( )
A.A与B,A与C均相互独立
B.A 与B相互独立,A与C互斥
C.A与B,A与C均互斥
D.A与B互斥,A与C相互独立
2.某同学做对某套试卷中每一个选择题的概率都为0.9,则他连续做对第1题和第2题的概率是( )
A.0.64 B.0.56 C.0.81 D.0.99
3.袋中装有3个白球和两个黑球,从中不放回地摸球,记事件A=“第一次摸到白球”,事件B=“第二次摸到白球”,则A与B是( )
A.互斥事件
B.相互独立事件
C.对立事件
D.不相互独立事件
10.2事件的相互独立性导学案
教学目标与核心素养
1.理解两事件相互独立的含义;
2.结合古典概型, 利用独立事件、 互斥事件的概率公式, 计算概率, 并能灵活应用
素养目标:
1.体会特殊与一般、 或然与必然、 化归与转化、 分类讨论等数学思想
2.渗透直观想象、 数学抽象、 逻辑推理、 数学运算等核心养
二、知识回顾
1、什么是互斥事件?
2、什么是对立事件?
三、探究新知
试验1:分别抛掷两枚质地均匀的硬币,A=“第一枚硬币正面朝上”,B=“第二枚硬币正面朝上”。
(1)事件A的发生是否影响事件B的概率?
(2)计算试验1中的P(A),P(B),P(AB),你有什么发现?
在该试验中,用1表示硬币“正面朝上”,用0表示“反面朝上”,则
样本空间Ω={( , ),( , ),( , ),( , )},包含4 个等可能的样本点。
而A={( , ),( , )},B={( , ),( , )}
所以AB={(1,0)}
由古典概率模型概率计算公式,
得P(A)=P(B)= ,P(AB)= , 于是 P( )=P( )P( )
试验2:一个袋子中装有标号分别是1,2,3,4的4个球,除标号外没有其他差异。采用有放回方式从袋中依次任意摸出两球。设A=“第一次摸到球的标号小于3”,B=“第二次摸到球的标号小于3”。
事件A的发生是否影响事件B的概率?
计算试验2中的P(A),P(B),P(AB),你有什么发现?
第一次m 第二次n
1 2 3 4
1 ( , ) ( , ) ( , ) ( , )
2 ( , ) ( , ) ( , ) ( , )
3 ( , ) ( , ) ( , ) ( , )
4 ( , ) ( , ) ( , ) ( , )
在该试验中,样本空间Ω={(m,n)|m,n∈{1,2,3,4}}共16个等可能的样本点
而A={(1,1),(1,2),(1,3),(1,4),(2,1),(2,2),(2,3),(2,4)}
B={(1,1),(1,2),(2,1),(2,2),(3,1),(3,2),(4,1),(4,2)}
AB={(1,1),(1,2),(2,1),(2,2)}
所以P(A)=P(B)= ,P(AB)= , 于是 P( )=P( )P( )
积事件AB的概率恰好等于事件A、B概率的乘积。
变式:一个袋子中有标号分别为1,2,3,4的4个球,除标号外没有其他差异。采用不放回方式从中任意摸球两次。记事件A=“第一次摸出球的标号小于3”,事件B=“第二次摸出球的标号小于3”,那么事件A与B是否相互独立?
解:因为样本空间Ω={(m,n)|m,n∈{1,2,3,4},且m≠n}共12个等可能的样本点
第一次m 第二次n
1 2 3 4
1 ( , ) ( , ) ( , )
2 ( , ) ( , ) ( , )
3 ( , ) ( , ) ( , )
4 ( , ) ( , ) ( , )
A={(1,2),(1,3),(1,4),(2,1),(2,3),(2,4)}
B={(1,2),(2,1),(3,1),(3,2),(4,1),(4,2)}
AB={ }
所以P(A)=P(B)= ,P(AB)= , 于是 P( )=P( )P( )
四、事件的相互独立性定义
直观定义:
事件A(或B)发生与否不影响事件B(或A)发生的概 率,则称事件A和B是相互独立事件.
数学定义
对任意两个事件A与B,如果P(AB)=P(A)P(B)成立,则称事件A与事件B相互独立,简称为独立。
判断题:下列事件哪些是相互独立事件?
①篮球比赛的“罚球两次”中
事件A:第一次罚球,球进了. 事件B:第二次罚球,球进了
②抛掷两枚骰子
事件A:第一枚骰子出现偶数点. 事件B:第二枚骰子出现奇数
③袋中有三个红球,两个白球,采取不放回的取球.
事件A:第一次从中任取一个球是白球. 事件B:第二次从中任取一个球是白球.
④袋中有三个红球,两个白球,采取有放回的取球.
事件A:第一次从中任取一个球是白球. 事件B:第二次从中任取一个球是白球.
相互独立事件的性质
若事件A与B相互独立, 则以下三对事件也相互独立: 、 、
必然事件及不可能事件与任何事件A
五、例题解析
例题讲解
例.甲、乙两名射击运动员进行设计比赛,甲的中靶概率为0.8,乙的中靶概率为0.9,求下列事件的概率:
(1)两人都中靶;(2)恰好有一人中靶;
(3)两人都脱靶;(4)至少有一人中靶。
六课堂小结
相互独立事件的定义
相互独立事件的性质
判断两个事件相互独立的方法:①定义法:P(AB)=P(A)P(B)②直接法:由事件本身的性质直接判断两个事件的发生是否相互影响。
趣味小知识
俗话说“三个臭皮匠,顶上一个诸葛亮”.假设三人解决某一问题的概率均为0.5,且相互独立。诸葛亮解决该问题的概率为0.8.你能从数学角度解决这句话的含义吗?
七、目标检测设计
1.袋内有3个白球和2个黑球,从中有放回地摸球,用A表示“第一次摸到白球”,如果“第二次摸到白球”记为B,否则记为C,那么事件A与B,A与C的关系是( )
A.A与B,A与C均相互独立
B.A 与B相互独立,A与C互斥
C.A与B,A与C均互斥
D.A与B互斥,A与C相互独立
2.某同学做对某套试卷中每一个选择题的概率都为0.9,则他连续做对第1题和第2题的概率是( )
A.0.64 B.0.56 C.0.81 D.0.99
3.袋中装有3个白球和两个黑球,从中不放回地摸球,记事件A=“第一次摸到白球”,事件B=“第二次摸到白球”,则A与B是( )
A.互斥事件
B.相互独立事件
C.对立事件
D.不相互独立事件
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
