2022-2023学年鲁教版(五四制)六年级数学上册 第3章整式及其加减 同步练习题(word版含解析)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)六年级数学上册 第3章整式及其加减 同步练习题(word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 135.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览




文档简介
2022-2023学年鲁教版七年级数学上册《第3章整式及其加减》同步练习题(附答案)
一.选择题
1.下列各式:a2+5,﹣3,a2﹣3a+2,π,,,其中整式有( )
A.3个 B.4个 C.5个 D.6个
2.下列各式中,与2a2b为同类项的是( )
A.﹣2a2b B.﹣2ab C.2ab2 D.2a2
3.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是( )
A.x+y B.10xy C.10(x+y) D.10x+y
4.下列说法中,正确的是( )
A.1不是单项式 B.﹣的系数是﹣5
C.﹣x2y是3次单项式 D.2x2+xy﹣1是四次三项式
5.下列各式中一定成立的是( )
A.﹣(b﹣a)=a﹣b B.﹣(b﹣a)=﹣b﹣a
C.﹣(a+b)=﹣a+b D.﹣(a﹣b)=﹣a﹣b
6.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元 B.(20a+24)元
C.(17a+3.6)元 D.(20a+3.6)元
7.若代数式x2+ax﹣(bx2﹣x﹣3)的值与字母x无关,则b﹣a的值为( )
A.2 B.1 C.0 D.﹣1
8.某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )
A.先打九五折,再打九五折
B.先提价50%,再打六折
C.先提价30%,再降价30%
D.先提价25%,再降价25%
9.已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )
A.31 B.﹣31 C.41 D.﹣41
10.按如图所示的运算程序,若输入x=3,y=2,则输出结果为( )
A.10 B.13 C.25 D.36
11.对于任意的有理数a,b,如果满足+=,那么我们称这一对数a,b为“相随数对”,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]=( )
A.﹣2 B.﹣1 C.2 D.3
12.根据图中数字的规律,若第n个图中的q=143,则p的值为( )
A.100 B.121 C.144 D.169
13.如果﹣5am﹣1b3与6a4b2﹣3n是同类项,那么m和n的值分别为( )
A.3和4 B.5和 C.5和 D.4和
14.现代的数学符号体系,不仅使得数学语言变得简洁明了,还能更好地帮助人们总结出便于运算的各种运算法则,简明地揭示数量之间的相互关系.我国在1905年清朝学堂的课本中还用“ ⊥”来表示相当于的代数式,观察其中的规律,化简“⊥ ”后得( )
A. B. C. D.
二.填空题
15.计算:2a2﹣(a2+2)= .
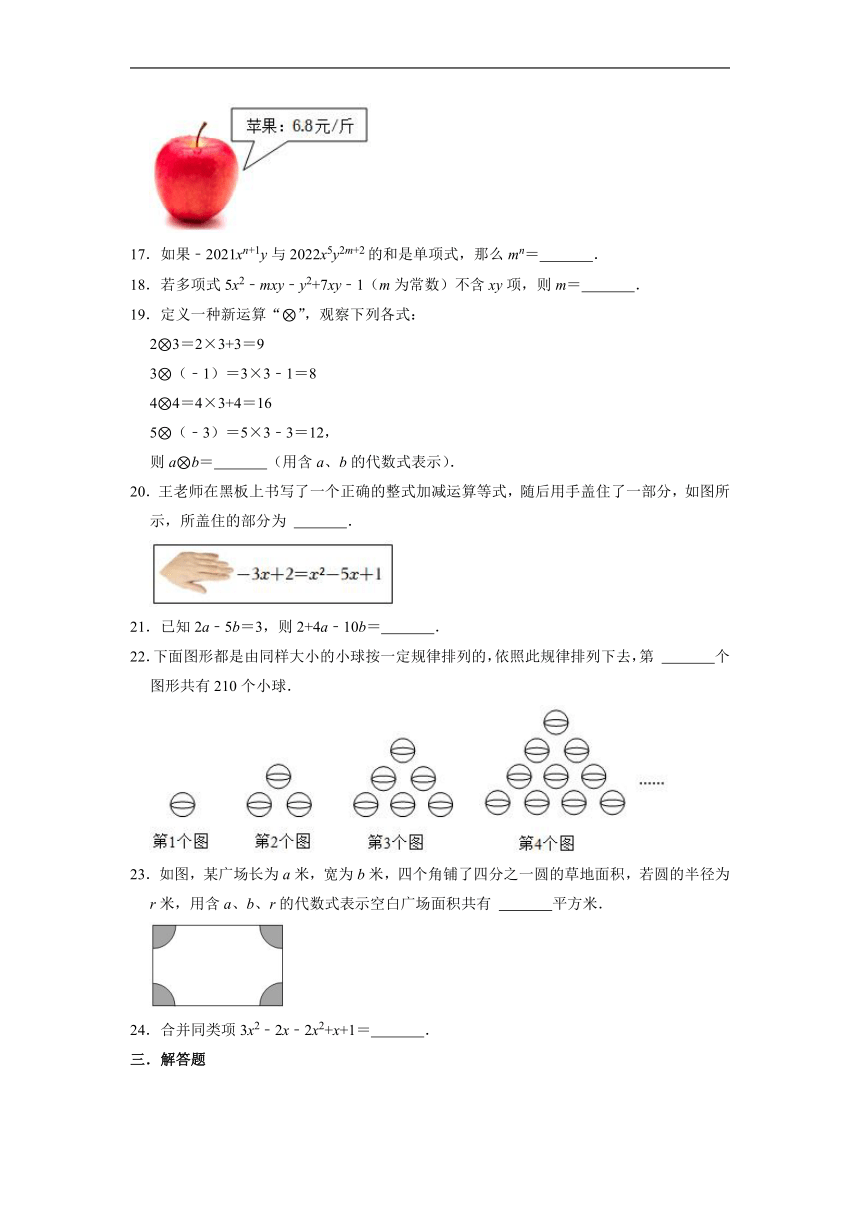
16.某超市的苹果价格如图,试说明代数式100﹣6.8x的实际意义 .
17.如果﹣2021xn+1y与2022x5y2m+2的和是单项式,那么mn= .
18.若多项式5x2﹣mxy﹣y2+7xy﹣1(m为常数)不含xy项,则m= .
19.定义一种新运算“ ”,观察下列各式:
2 3=2×3+3=9
3 (﹣1)=3×3﹣1=8
4 4=4×3+4=16
5 (﹣3)=5×3﹣3=12,
则a b= (用含a、b的代数式表示).
20.王老师在黑板上书写了一个正确的整式加减运算等式,随后用手盖住了一部分,如图所示,所盖住的部分为 .
21.已知2a﹣5b=3,则2+4a﹣10b= .
22.下面图形都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第 个图形共有210个小球.
23.如图,某广场长为a米,宽为b米,四个角铺了四分之一圆的草地面积,若圆的半径为r米,用含a、b、r的代数式表示空白广场面积共有 平方米.
24.合并同类项3x2﹣2x﹣2x2+x+1= .
三.解答题
25.先化简再求值:3(a2﹣2ab)﹣[3a2﹣2b+2(ab+b)],其中a、b满足(a+)2+|b﹣3|=0.
26.为改善居民居住条件,让人民群众生活更方便更美好,国家出台了改造提升城镇老旧小区政策.在我县“老城换新颜”小区改造中,某小区规划修建一个广场(平面图形如图所示):
(1)用含m,n的代数式表示广场(阴影部分)的面积S;
(2)若m=60米,n=50米,求出该广场的面积.
27.某同学做一道题,已知两个多项式A、B,求A﹣2B的值.他误将“A﹣2B”看成“A+2B”,经过正确计算得到的结果是x2+14x﹣6.已知A=﹣2x2+5x﹣1.
(1)请你帮助这位同学求出正确的结果;
(2)若x是最大的负整数,求A﹣2B的值.
28.阅读材料:“整体思想”是中学数学的重要思想方法,在解题中会经常用到.我们知道,合并同类项:4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).
尝试应用:
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是 .
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值.
拓展探索:
(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
29.已知表②,表③分别是从表①中选取的一部分,表①中第一行第四个数是3,第二行第三个数是5,根据表①中的规律,解答下列问题:
(1)表①中第四行第五个数是 ;
(2)表②,表③中的a,b的和是 ;
(3)求表①中第四行第几个数是107?
(4)表①中第n行第7个数是 (用含n的代数式表示).
30.如图:在数轴上点A表示数a,点B表示数b,点C表示数c,数a是多项式﹣2x2﹣3x+1的一次项系数,数b是最大的负整数,数c是单项式﹣x2y的次数.
(1)a= ,b= ,c= .
(2)点A,B,C开始在数轴上运动,若点B和点C分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,点A以每秒2个单位长度的速度向左运动,t秒过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB= ,BC= .(用含t的代数式表示)
(3)试问:3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出这个值.
31.下面是小彬同学进行整式化简的过程,请认真阅读并完成相应任务.
(1)填空:
①以上化简步骤中,第一步的依据是 ;
②以上化简步骤中,第 步开始不符合题意,这一步错误的原因是 ;
(2)请写出该整式正确的化简过程,并计算当x=﹣1,y=﹣时该整式的值.
32.设A=2x2+x,B=kx2﹣(3x2﹣x+1).
(1)当x=﹣1时,求A的值;
(2)小明认为不论k取何值,A﹣B的值都无法确定,小红认为k可以找到适当的数,使代数式A﹣B的值是常数.你认为谁的说法正确?请说明理由.
参考答案
一.选择题
1.解:整式有:a2+5,﹣3,a2﹣3a+2,π,共有4个.
故选:B.
2.解:2a2b中含有两个字母:a、b,且a的指数是2,b的指数是1,观察选项,与2a2b是同类项的是﹣2a2b.
故选:A.
3.解:一个两位数,它的十位数字是x,个位数字是y,这个两位数10x+y.
故选:D.
4.解:1是单项式,故A错误,不符合题意;
﹣的系数是﹣,故B错误,不符合题意;
﹣x2y是3次单项式,故C正确,符合题意;
2x2+xy﹣1是二次三项式,故D错误,不符合题意;
故选:C.
5.解:A.﹣(b﹣a)=a﹣b,原去括号正确,故此选项符合题意;
B.﹣(b﹣a)=﹣b+a,原去括号错误,故此选项不符合题意;
C.﹣(a+b)=﹣a﹣b,原去括号错误,故此选项不符合题意;
D.﹣(a﹣b)=﹣a+b,原去括号错误,故此选项不符合题意;
故选:A.
6.解:根据题意知:17a+(20﹣17)(a+1.2)=(20a+3.6)(元).
故选:D.
7.解:x2+ax﹣(bx2﹣x﹣3)
=x2+ax﹣bx2+x+3
=(1﹣b)x2+(a+1)x+3,
∵代数式的值与字母x无关,
∴1﹣b=0,a+1=0,
∴b=1,a=﹣1,
∴b﹣a=1﹣(﹣1)
=1+1
=2,
故选:A.
8.解:设商品原标价为a元,
A.先打九五折,再打九五折的售价为:0.95×0.95a=0.9025a(元);
B.先提价50%,再打六折的售价为:(1+50%)×0.6a=0.9a(元);
C.先提价30%,再降价30%的售价为:(1+30%)(1﹣30%)a=0.91a(元);
D.先提价25%,再降价25%的售价为:(1+25%)(1﹣25%)a=0.9375a(元);
∵0.9a<0.9025a<0.91a<0.9375a,
∴B选项的调价方案调价后售价最低,
故选:B.
9.解:∵x2﹣3x﹣12=0,
∴x2﹣3x=12.
原式=﹣3(x2﹣3x)+5=﹣3×12+5=﹣36+5=﹣31.
故选:B.
10.解:∵x=3,3是奇数,
∴将x=3,y=2代入x2+y2,
原式=32+22=13,
故选:B.
11.解:∵(m,n)是“相随数对”,
∴+=,
∴=,
即9m+4n=0,
∴3m+2[3m+(2n﹣1)]
=3m+2[3m+2n﹣1]
=3m+6m+4n﹣2
=9m+4n﹣2
=0﹣2
=﹣2,
故选:A.
12.解:通过观察可得规律:p=n2,q=(n+1)2﹣1,
∵q=143,
∴(n+1)2﹣1=143,
解得:n=11,
∴p=n2=112=121,
故选:B.
13.解:∵﹣5am﹣1b3与6a4b2﹣3n是同类项,
∴m﹣1=4,2﹣3n=3,
解得:m=5,n=.
故选:B.
14.解:由题意可得,
原式=
=
=
=,
故选:A.
二.填空题
15.解:原式=2a2﹣a2﹣2=a2﹣2,
故答案为:a2﹣2.
16.解:代数式100﹣6.8x的实际意义为:用100元买每斤6.8元的苹果x斤余下的钱.
故答案为:用100元买每斤6.8元的苹果x斤余下的钱.
17.解:∵﹣2021xn+1y与2022x5y2m+2的和是单项式,
∴﹣2021xn+1y与2022x5y2m+2是同类项,
∴n+1=5,2m+2=1,
解得n=4,m=﹣,
∴mn==.
故答案为:.
18.解:5x2﹣mxy﹣y2+7xy﹣1=5x2+(7﹣m)xy﹣y2﹣1,
∵多项式5x2﹣mxy﹣y2+7xy﹣1(m为常数)不含xy项,
∴7﹣m=0,
解得,m=7,
故答案为:7.
19.解:∵2 3=2×3+3=9,
3 (﹣1)=3×3﹣1=8,
4 4=4×3+4=16,
5 (﹣3)=5×3﹣3=12,
∴a b=3a+b,
故答案为:3a+b.
20.解:由题意可得,所盖住的部分为:
x2﹣5x+1﹣(﹣3x+2)
=x2﹣5x+1+3x﹣2
=x2﹣2x﹣1.
故答案为:x2﹣2x﹣1.
21.解:∵2a﹣5b=3,
∴2+4a﹣10b
=2+2(2a﹣5b)
=2+2×3
=8,
故答案为:8.
22.解:第1个图中有1个小球,
第2个图中有3个小球,3=1+2,
第3个图中有6个小球,6=1+2+3,
第4个图中有10个小球,10=1+2+3+4,
……
照此规律,第n个图中有1+2+3+……+n=个小球,
当时,
解之得:n1=20,n2=﹣21(舍),
故答案为:20.
23.解:根据题意,空白广场面积共有(ab﹣πr2)平方米,
故答案为:(ab﹣πr2).
24.解:3x2﹣2x﹣2x2+x+1=x2﹣x+1,
故答案为:x2﹣x+1.
三.解答题
25.解:∵(a+)2+|b﹣3|=0,
∴a+=0,b﹣3=0,
∴a=﹣,b=3,
3(a2﹣2ab)﹣[3a2﹣2b+2(ab+b)]
=3a2﹣6ab)﹣3a2+2b﹣2(ab+b)
=3a2﹣6ab﹣3a2+2b﹣2ab﹣2b
=﹣8ab,
当a=﹣,b=3时,
原式=﹣8×(﹣)×3=12.
26.解:(1)由题意得,
S=2m 2n﹣(2n﹣n﹣0.5n)m
=4mn﹣0.5mn
=3.5mn;
(2)∵m=60米,n=50米,
∴S=3.5mn=3.5×60×50=10500.
答:该广场的面积为10500平方米.
27.解:(1)由题意得:
2B=x2+14x﹣6﹣(﹣2x2+5x﹣1)
=x2+14x﹣6+2x2﹣5x+1
=3x2+9x﹣5,
所以,A﹣2B=﹣2x2+5x﹣1﹣(3x2+9x﹣5)
=﹣2x2+5x﹣1﹣3x2﹣9x+5
=﹣5x2﹣4x+4;
(2)由x是最大的负整数,可知x=﹣1,
所以,A﹣2B=﹣5×(﹣1)2﹣4×(﹣1)+4
=﹣5+4+4
=3.
28.解:(1)3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2
=(3﹣6+2)(a﹣b)2
=﹣(a﹣b)2;
(2)∵x2﹣2y=4,
∴原式=3(x2﹣2y)﹣21
=3×4﹣21
=12﹣21
=﹣9;
(3)∵a﹣2b=3,2b﹣c=﹣5,c﹣d=10,
∴原式=a﹣c+2b﹣d﹣2b+c
=(a﹣2b)+(2b﹣c)+(c﹣d)
=3﹣5+10
=8.
29.解:(1)由表格①可得第四行后面每个数字是前面数字+4,
∴第五个数为15+4=19.
故答案为:19.
(2)根据表②位于表格第三列,下面的数字是上面数字+3,
∴a=14+3=17,
③位于表格中第6,7列,b位于第7列,
∴b=13+7=20,
∴a+b=37.
故答案为37.
(3)表①中第四行第一个数为3,第n个数为3+4(n﹣1),
当3+4(n﹣1)=107时,
解得n=27.
(4)第n行第一个数为n﹣1,第七个数为n﹣1+(7﹣1)n=7n﹣1.
故答案为:7n﹣1.
30.解:(1)﹣2x2﹣3x+1 的一次项系数是﹣3,最大的负整数是﹣1,单项式的次数是3,
∴a=﹣3,b=﹣1,c=3,
故答案为:﹣3,﹣1,3;
(2)点A以每秒2个单位长度的速度向左运动,
∴运动后对应的点为﹣3﹣2t,
点B以每秒1个单位长度向右运动,
∴运动后对应的点为﹣1+t,
点C以每秒3个单位长度的速度向右运动,
∴运动后对应的点为3+3t;
∴t秒钟后,
AB=|﹣1+t﹣(﹣3﹣2t)|=3t+2;
BC=|3+3t﹣(﹣1+t)|=2t+4.
故答案为:3t+2;2t+4;
(3)3BC﹣2AB
=3(2t+4)﹣2(3t+2)
=6t+12﹣6t﹣4
=8.
计算3BC﹣2AB的结果为8,故值不变.
31.解:(1)①以上化简步骤中,第一步的依据是乘法分配律;
故答案为:乘法分配律.
②以上化简步骤中,第二步开始出现不符合题意,这一步错误的原因是去括号没变号;
故答案为:二,去括号没变号.
(2)原式=3x2y+2xy﹣(2xy+2x2y)
=3x2y+2xy﹣2xy﹣2x2y
=x2y,
当x=﹣1,y=﹣时,
原式==﹣.
32.解:(1)当x=﹣1时,
A=2×(﹣1)2+(﹣1)
=2×1﹣1
=2﹣1
=1;
(2)小红的说法正确,理由如下:
∵A﹣B=(2x2+x)﹣[kx2﹣(3x2﹣x+1)]
=2x2+x﹣kx2+3x2﹣x+1
=(5﹣k)x2+1
∴当k=5时,A﹣B=1
∴小红的说法是正确的.
一.选择题
1.下列各式:a2+5,﹣3,a2﹣3a+2,π,,,其中整式有( )
A.3个 B.4个 C.5个 D.6个
2.下列各式中,与2a2b为同类项的是( )
A.﹣2a2b B.﹣2ab C.2ab2 D.2a2
3.一个两位数,它的十位数字是x,个位数字是y,那么这个两位数是( )
A.x+y B.10xy C.10(x+y) D.10x+y
4.下列说法中,正确的是( )
A.1不是单项式 B.﹣的系数是﹣5
C.﹣x2y是3次单项式 D.2x2+xy﹣1是四次三项式
5.下列各式中一定成立的是( )
A.﹣(b﹣a)=a﹣b B.﹣(b﹣a)=﹣b﹣a
C.﹣(a+b)=﹣a+b D.﹣(a﹣b)=﹣a﹣b
6.某地居民生活用水收费标准:每月用水量不超过17立方米,每立方米a元;超过部分每立方米(a+1.2)元.该地区某用户上月用水量为20立方米,则应缴水费为( )
A.20a元 B.(20a+24)元
C.(17a+3.6)元 D.(20a+3.6)元
7.若代数式x2+ax﹣(bx2﹣x﹣3)的值与字母x无关,则b﹣a的值为( )
A.2 B.1 C.0 D.﹣1
8.某超市出售一商品,有如下四种在原标价基础上调价的方案,其中调价后售价最低的是( )
A.先打九五折,再打九五折
B.先提价50%,再打六折
C.先提价30%,再降价30%
D.先提价25%,再降价25%
9.已知x2﹣3x﹣12=0,则代数式﹣3x2+9x+5的值是( )
A.31 B.﹣31 C.41 D.﹣41
10.按如图所示的运算程序,若输入x=3,y=2,则输出结果为( )
A.10 B.13 C.25 D.36
11.对于任意的有理数a,b,如果满足+=,那么我们称这一对数a,b为“相随数对”,记为(a,b).若(m,n)是“相随数对”,则3m+2[3m+(2n﹣1)]=( )
A.﹣2 B.﹣1 C.2 D.3
12.根据图中数字的规律,若第n个图中的q=143,则p的值为( )
A.100 B.121 C.144 D.169
13.如果﹣5am﹣1b3与6a4b2﹣3n是同类项,那么m和n的值分别为( )
A.3和4 B.5和 C.5和 D.4和
14.现代的数学符号体系,不仅使得数学语言变得简洁明了,还能更好地帮助人们总结出便于运算的各种运算法则,简明地揭示数量之间的相互关系.我国在1905年清朝学堂的课本中还用“ ⊥”来表示相当于的代数式,观察其中的规律,化简“⊥ ”后得( )
A. B. C. D.
二.填空题
15.计算:2a2﹣(a2+2)= .
16.某超市的苹果价格如图,试说明代数式100﹣6.8x的实际意义 .
17.如果﹣2021xn+1y与2022x5y2m+2的和是单项式,那么mn= .
18.若多项式5x2﹣mxy﹣y2+7xy﹣1(m为常数)不含xy项,则m= .
19.定义一种新运算“ ”,观察下列各式:
2 3=2×3+3=9
3 (﹣1)=3×3﹣1=8
4 4=4×3+4=16
5 (﹣3)=5×3﹣3=12,
则a b= (用含a、b的代数式表示).
20.王老师在黑板上书写了一个正确的整式加减运算等式,随后用手盖住了一部分,如图所示,所盖住的部分为 .
21.已知2a﹣5b=3,则2+4a﹣10b= .
22.下面图形都是由同样大小的小球按一定规律排列的,依照此规律排列下去,第 个图形共有210个小球.
23.如图,某广场长为a米,宽为b米,四个角铺了四分之一圆的草地面积,若圆的半径为r米,用含a、b、r的代数式表示空白广场面积共有 平方米.
24.合并同类项3x2﹣2x﹣2x2+x+1= .
三.解答题
25.先化简再求值:3(a2﹣2ab)﹣[3a2﹣2b+2(ab+b)],其中a、b满足(a+)2+|b﹣3|=0.
26.为改善居民居住条件,让人民群众生活更方便更美好,国家出台了改造提升城镇老旧小区政策.在我县“老城换新颜”小区改造中,某小区规划修建一个广场(平面图形如图所示):
(1)用含m,n的代数式表示广场(阴影部分)的面积S;
(2)若m=60米,n=50米,求出该广场的面积.
27.某同学做一道题,已知两个多项式A、B,求A﹣2B的值.他误将“A﹣2B”看成“A+2B”,经过正确计算得到的结果是x2+14x﹣6.已知A=﹣2x2+5x﹣1.
(1)请你帮助这位同学求出正确的结果;
(2)若x是最大的负整数,求A﹣2B的值.
28.阅读材料:“整体思想”是中学数学的重要思想方法,在解题中会经常用到.我们知道,合并同类项:4x﹣2x+x=(4﹣2+1)x=3x,类似地,我们把(a+b)看成一个整体,则4(a+b)﹣2(a+b)+(a+b)=(4﹣2+1)(a+b)=3(a+b).
尝试应用:
(1)把(a﹣b)2看成一个整体,合并3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2的结果是 .
(2)已知x2﹣2y=4,求3x2﹣6y﹣21的值.
拓展探索:
(3)已知a﹣2b=3,2b﹣c=﹣5,c﹣d=10,求(a﹣c)+(2b﹣d)﹣(2b﹣c)的值.
29.已知表②,表③分别是从表①中选取的一部分,表①中第一行第四个数是3,第二行第三个数是5,根据表①中的规律,解答下列问题:
(1)表①中第四行第五个数是 ;
(2)表②,表③中的a,b的和是 ;
(3)求表①中第四行第几个数是107?
(4)表①中第n行第7个数是 (用含n的代数式表示).
30.如图:在数轴上点A表示数a,点B表示数b,点C表示数c,数a是多项式﹣2x2﹣3x+1的一次项系数,数b是最大的负整数,数c是单项式﹣x2y的次数.
(1)a= ,b= ,c= .
(2)点A,B,C开始在数轴上运动,若点B和点C分别以每秒1个单位长度和每秒3个单位长度的速度向右运动,点A以每秒2个单位长度的速度向左运动,t秒过后,若点A与点B之间的距离表示为AB,点B与点C之间的距离表示为BC,则AB= ,BC= .(用含t的代数式表示)
(3)试问:3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求出这个值.
31.下面是小彬同学进行整式化简的过程,请认真阅读并完成相应任务.
(1)填空:
①以上化简步骤中,第一步的依据是 ;
②以上化简步骤中,第 步开始不符合题意,这一步错误的原因是 ;
(2)请写出该整式正确的化简过程,并计算当x=﹣1,y=﹣时该整式的值.
32.设A=2x2+x,B=kx2﹣(3x2﹣x+1).
(1)当x=﹣1时,求A的值;
(2)小明认为不论k取何值,A﹣B的值都无法确定,小红认为k可以找到适当的数,使代数式A﹣B的值是常数.你认为谁的说法正确?请说明理由.
参考答案
一.选择题
1.解:整式有:a2+5,﹣3,a2﹣3a+2,π,共有4个.
故选:B.
2.解:2a2b中含有两个字母:a、b,且a的指数是2,b的指数是1,观察选项,与2a2b是同类项的是﹣2a2b.
故选:A.
3.解:一个两位数,它的十位数字是x,个位数字是y,这个两位数10x+y.
故选:D.
4.解:1是单项式,故A错误,不符合题意;
﹣的系数是﹣,故B错误,不符合题意;
﹣x2y是3次单项式,故C正确,符合题意;
2x2+xy﹣1是二次三项式,故D错误,不符合题意;
故选:C.
5.解:A.﹣(b﹣a)=a﹣b,原去括号正确,故此选项符合题意;
B.﹣(b﹣a)=﹣b+a,原去括号错误,故此选项不符合题意;
C.﹣(a+b)=﹣a﹣b,原去括号错误,故此选项不符合题意;
D.﹣(a﹣b)=﹣a+b,原去括号错误,故此选项不符合题意;
故选:A.
6.解:根据题意知:17a+(20﹣17)(a+1.2)=(20a+3.6)(元).
故选:D.
7.解:x2+ax﹣(bx2﹣x﹣3)
=x2+ax﹣bx2+x+3
=(1﹣b)x2+(a+1)x+3,
∵代数式的值与字母x无关,
∴1﹣b=0,a+1=0,
∴b=1,a=﹣1,
∴b﹣a=1﹣(﹣1)
=1+1
=2,
故选:A.
8.解:设商品原标价为a元,
A.先打九五折,再打九五折的售价为:0.95×0.95a=0.9025a(元);
B.先提价50%,再打六折的售价为:(1+50%)×0.6a=0.9a(元);
C.先提价30%,再降价30%的售价为:(1+30%)(1﹣30%)a=0.91a(元);
D.先提价25%,再降价25%的售价为:(1+25%)(1﹣25%)a=0.9375a(元);
∵0.9a<0.9025a<0.91a<0.9375a,
∴B选项的调价方案调价后售价最低,
故选:B.
9.解:∵x2﹣3x﹣12=0,
∴x2﹣3x=12.
原式=﹣3(x2﹣3x)+5=﹣3×12+5=﹣36+5=﹣31.
故选:B.
10.解:∵x=3,3是奇数,
∴将x=3,y=2代入x2+y2,
原式=32+22=13,
故选:B.
11.解:∵(m,n)是“相随数对”,
∴+=,
∴=,
即9m+4n=0,
∴3m+2[3m+(2n﹣1)]
=3m+2[3m+2n﹣1]
=3m+6m+4n﹣2
=9m+4n﹣2
=0﹣2
=﹣2,
故选:A.
12.解:通过观察可得规律:p=n2,q=(n+1)2﹣1,
∵q=143,
∴(n+1)2﹣1=143,
解得:n=11,
∴p=n2=112=121,
故选:B.
13.解:∵﹣5am﹣1b3与6a4b2﹣3n是同类项,
∴m﹣1=4,2﹣3n=3,
解得:m=5,n=.
故选:B.
14.解:由题意可得,
原式=
=
=
=,
故选:A.
二.填空题
15.解:原式=2a2﹣a2﹣2=a2﹣2,
故答案为:a2﹣2.
16.解:代数式100﹣6.8x的实际意义为:用100元买每斤6.8元的苹果x斤余下的钱.
故答案为:用100元买每斤6.8元的苹果x斤余下的钱.
17.解:∵﹣2021xn+1y与2022x5y2m+2的和是单项式,
∴﹣2021xn+1y与2022x5y2m+2是同类项,
∴n+1=5,2m+2=1,
解得n=4,m=﹣,
∴mn==.
故答案为:.
18.解:5x2﹣mxy﹣y2+7xy﹣1=5x2+(7﹣m)xy﹣y2﹣1,
∵多项式5x2﹣mxy﹣y2+7xy﹣1(m为常数)不含xy项,
∴7﹣m=0,
解得,m=7,
故答案为:7.
19.解:∵2 3=2×3+3=9,
3 (﹣1)=3×3﹣1=8,
4 4=4×3+4=16,
5 (﹣3)=5×3﹣3=12,
∴a b=3a+b,
故答案为:3a+b.
20.解:由题意可得,所盖住的部分为:
x2﹣5x+1﹣(﹣3x+2)
=x2﹣5x+1+3x﹣2
=x2﹣2x﹣1.
故答案为:x2﹣2x﹣1.
21.解:∵2a﹣5b=3,
∴2+4a﹣10b
=2+2(2a﹣5b)
=2+2×3
=8,
故答案为:8.
22.解:第1个图中有1个小球,
第2个图中有3个小球,3=1+2,
第3个图中有6个小球,6=1+2+3,
第4个图中有10个小球,10=1+2+3+4,
……
照此规律,第n个图中有1+2+3+……+n=个小球,
当时,
解之得:n1=20,n2=﹣21(舍),
故答案为:20.
23.解:根据题意,空白广场面积共有(ab﹣πr2)平方米,
故答案为:(ab﹣πr2).
24.解:3x2﹣2x﹣2x2+x+1=x2﹣x+1,
故答案为:x2﹣x+1.
三.解答题
25.解:∵(a+)2+|b﹣3|=0,
∴a+=0,b﹣3=0,
∴a=﹣,b=3,
3(a2﹣2ab)﹣[3a2﹣2b+2(ab+b)]
=3a2﹣6ab)﹣3a2+2b﹣2(ab+b)
=3a2﹣6ab﹣3a2+2b﹣2ab﹣2b
=﹣8ab,
当a=﹣,b=3时,
原式=﹣8×(﹣)×3=12.
26.解:(1)由题意得,
S=2m 2n﹣(2n﹣n﹣0.5n)m
=4mn﹣0.5mn
=3.5mn;
(2)∵m=60米,n=50米,
∴S=3.5mn=3.5×60×50=10500.
答:该广场的面积为10500平方米.
27.解:(1)由题意得:
2B=x2+14x﹣6﹣(﹣2x2+5x﹣1)
=x2+14x﹣6+2x2﹣5x+1
=3x2+9x﹣5,
所以,A﹣2B=﹣2x2+5x﹣1﹣(3x2+9x﹣5)
=﹣2x2+5x﹣1﹣3x2﹣9x+5
=﹣5x2﹣4x+4;
(2)由x是最大的负整数,可知x=﹣1,
所以,A﹣2B=﹣5×(﹣1)2﹣4×(﹣1)+4
=﹣5+4+4
=3.
28.解:(1)3(a﹣b)2﹣6(a﹣b)2+2(a﹣b)2
=(3﹣6+2)(a﹣b)2
=﹣(a﹣b)2;
(2)∵x2﹣2y=4,
∴原式=3(x2﹣2y)﹣21
=3×4﹣21
=12﹣21
=﹣9;
(3)∵a﹣2b=3,2b﹣c=﹣5,c﹣d=10,
∴原式=a﹣c+2b﹣d﹣2b+c
=(a﹣2b)+(2b﹣c)+(c﹣d)
=3﹣5+10
=8.
29.解:(1)由表格①可得第四行后面每个数字是前面数字+4,
∴第五个数为15+4=19.
故答案为:19.
(2)根据表②位于表格第三列,下面的数字是上面数字+3,
∴a=14+3=17,
③位于表格中第6,7列,b位于第7列,
∴b=13+7=20,
∴a+b=37.
故答案为37.
(3)表①中第四行第一个数为3,第n个数为3+4(n﹣1),
当3+4(n﹣1)=107时,
解得n=27.
(4)第n行第一个数为n﹣1,第七个数为n﹣1+(7﹣1)n=7n﹣1.
故答案为:7n﹣1.
30.解:(1)﹣2x2﹣3x+1 的一次项系数是﹣3,最大的负整数是﹣1,单项式的次数是3,
∴a=﹣3,b=﹣1,c=3,
故答案为:﹣3,﹣1,3;
(2)点A以每秒2个单位长度的速度向左运动,
∴运动后对应的点为﹣3﹣2t,
点B以每秒1个单位长度向右运动,
∴运动后对应的点为﹣1+t,
点C以每秒3个单位长度的速度向右运动,
∴运动后对应的点为3+3t;
∴t秒钟后,
AB=|﹣1+t﹣(﹣3﹣2t)|=3t+2;
BC=|3+3t﹣(﹣1+t)|=2t+4.
故答案为:3t+2;2t+4;
(3)3BC﹣2AB
=3(2t+4)﹣2(3t+2)
=6t+12﹣6t﹣4
=8.
计算3BC﹣2AB的结果为8,故值不变.
31.解:(1)①以上化简步骤中,第一步的依据是乘法分配律;
故答案为:乘法分配律.
②以上化简步骤中,第二步开始出现不符合题意,这一步错误的原因是去括号没变号;
故答案为:二,去括号没变号.
(2)原式=3x2y+2xy﹣(2xy+2x2y)
=3x2y+2xy﹣2xy﹣2x2y
=x2y,
当x=﹣1,y=﹣时,
原式==﹣.
32.解:(1)当x=﹣1时,
A=2×(﹣1)2+(﹣1)
=2×1﹣1
=2﹣1
=1;
(2)小红的说法正确,理由如下:
∵A﹣B=(2x2+x)﹣[kx2﹣(3x2﹣x+1)]
=2x2+x﹣kx2+3x2﹣x+1
=(5﹣k)x2+1
∴当k=5时,A﹣B=1
∴小红的说法是正确的.
