2022-2023学年鲁教版(五四制)六年级数学上册 第1章丰富的图形世界 常考题型达标测试题(word版含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)六年级数学上册 第1章丰富的图形世界 常考题型达标测试题(word版含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 268.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览




文档简介
2022-2023学年鲁教版六年级数学上册《第1章丰富的图形世界》
常考题型达标测试题(附答案)
一.选择题(共10小题,满分50分)
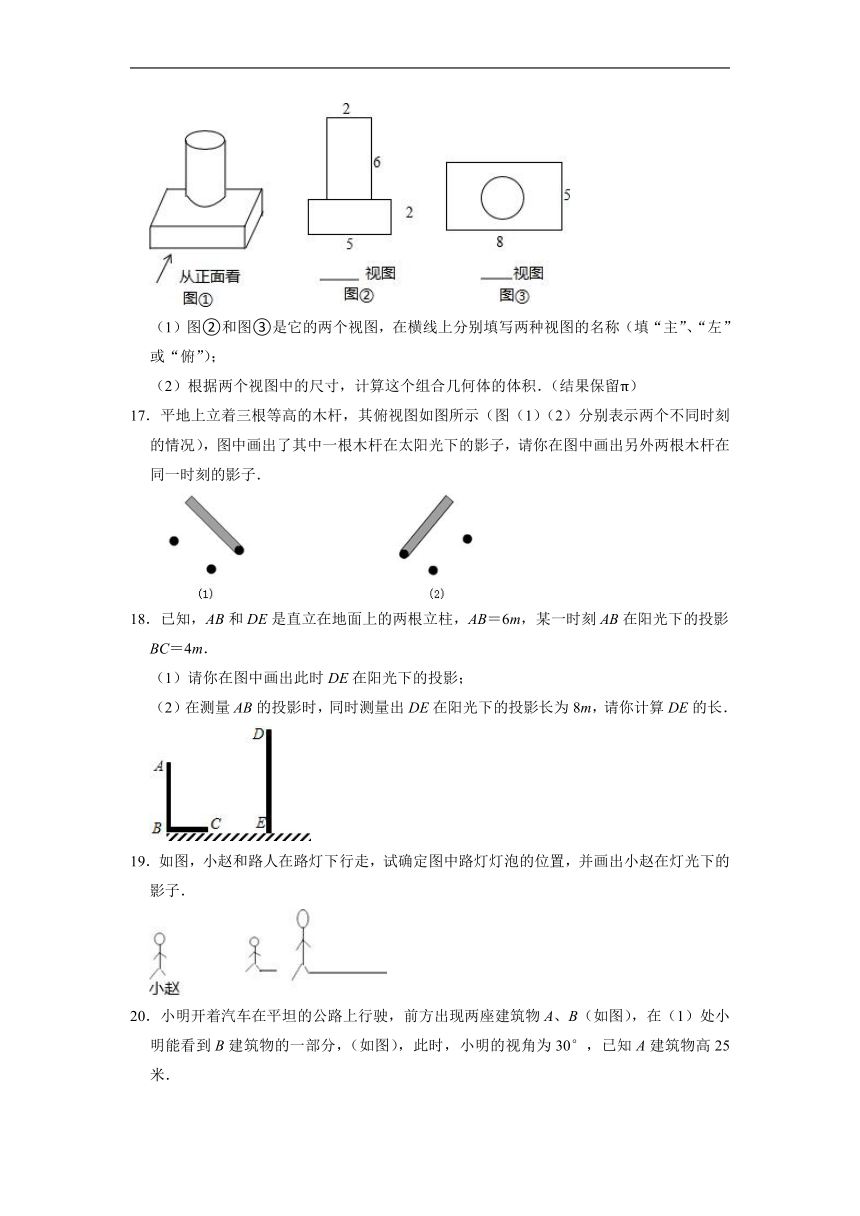
1.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A.1个 B.2个 C.3个 D.4个
2.一个正三棱柱和一个正四棱柱的底面边长和高都相等,当一只小猫只看到它的一个侧面时,它看到( )
A.正三棱柱的区域大 B.正四棱柱的区域大
C.两者的区域一样大 D.无法确定
3.如图放置的几何体的左视图是( )
A. B. C. D.
4.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
5.某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为( )
A.3π B.2π C.π D.12
6.观察如图所示的三种视图,与之对应的物体是( )
A. B. C. D.
7.如图为一个用正方体积木搭成的几何体的三视图,俯视图中方格上的数字表示该位置上积木累积的个数.若保证正视图和左视图成立,则a+b+c+d的最大值为( )
A.12 B.13 C.14 D.15
8.如图,是由一些完全相同的小正方体搭成的几何体的主视图和俯视图,则这个几何体的搭法有( )种.
A.3 B.4 C.5 D.6
9.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图,如图,按图中尺寸(单位:cm)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( )
A.1000cm2 B.1030cm2 C.1100cm2 D.1200cm2
10.如图是某工件的三视图,则此工件的表面积为( )
A.20πcm2 B.36πcm2 C.56πcm2 D.24πcm2
二.填空题(共5小题,满分25分)
11.一个圆锥的主视图是底边为12,底边上的高为8的等腰三角形,则这个圆锥的表面积为 cm2.
12.太阳光形成的投影是 ,手电筒、电灯泡所发出的光线形成的投影是 .
13.一天上午小红先参加了校运动会女子100m比赛,过一段时间又参加了女子400m比赛,如图是摄影师在同一位置拍摄的两张照片,那么 (填“甲”或“乙”照片)是参加400m比赛时照的.
14.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
15.从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是 .
三.解答题(共6小题,满分45分)
16.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
17.平地上立着三根等高的木杆,其俯视图如图所示(图(1)(2)分别表示两个不同时刻的情况),图中画出了其中一根木杆在太阳光下的影子,请你在图中画出另外两根木杆在同一时刻的影子.
18.已知,AB和DE是直立在地面上的两根立柱,AB=6m,某一时刻AB在阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.
19.如图,小赵和路人在路灯下行走,试确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
20.小明开着汽车在平坦的公路上行驶,前方出现两座建筑物A、B(如图),在(1)处小明能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)
21.先观察下图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
参考答案
一.选择题(共10小题,满分50分)
1.解:正方体从前往后看和从上往下看,看到的图形形状都是正方形,①符合题意;
球从前往后看和从上往下看,看到的图形形状都是圆,②符合题意;
圆锥从前往后看和从上往下看,看到的图形形状分别是三角形和圆,③不合题意;
圆柱从前往后看和从上往下看,看到的图形形状分别是矩形和圆,④不合题意,
故选:B.
2.解:正三棱柱和正四棱柱的底面边长和高相等,但是棱长不能确定,所以看到的区域大小不能确定.
故选:D.
3.解:左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
故选:C.
4.解:这样的几何体不止一种,而有多种摆法.
最少需要2+1+1+1=5(个)小立方块,最多需要2×3+1=7(个)小立方块.
因为用6个小立方块搭一个几何体,
所以它的左视图不可能是.
故选:D.
5.解:根据三视图可以判断该几何体为圆柱,圆柱的底面半径为1,高为3,
故体积为:πr2h=π×1×3=3π,
故选:A.
6.解:结合主视图和俯视图发现几何体的背面应该有个凸起,
故淘汰选项ABC,选D.
故选:D.
7.解:由正视图第1列和左视图第1列可知a最大为3,由正视图第2列和左视图第2列可知b最大为3,由正视图第3列和左视图第1列和第2列可知c最大为4,d最大为3,
则a+b+c+d的最大值为3+3+4+3=13.
故选:B.
8.解:由主视图易得这个几何体共有3层,由俯视图易得最底层有3个小正方体,第2列第二层和第3层的情况数有5种.
故选:C.
9.解:(18×12+18×10+12×10)×2
=(216+180+120)×2
=516×2
=1032(cm2),
故如果只考虑面积因素,采用面积1100cm2的铁板最合理.
故选:C.
10.解:由三视图,得:
OB=8÷2=4(cm),OA=3cm,
AB==5(cm),
圆锥的侧面积×8π×5=20π(cm2),
圆锥的底面积π×()2=16π(cm2),
圆锥的表面积20π+16π=36π(cm2).
故选:B.
二.填空题(共5小题,满分25分)
11.解:底面周长是12πcm,底面积是:π×(12÷2)2=36πcm2.
母线长是:=10cm,
则圆锥的侧面积是:π×(12÷2)×10=60πcm2,
则圆锥的表面积为36π+60π=96πcm2.
故答案是:96π.
12.解:∵由光线所形成的投影称为平行投影;有中心放射状光线所形成的投影称为中心投影.
∴太阳光形成的投影是平行投影,手电筒、电灯泡所发出的光线形成的投影是中心投影,
故答案为:平行投影,中心投影.
13.解:根据平行投影的规律:从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长;
∵比赛是在上午进行,
∴则甲照片是参加100m的,乙照片是参加400m的.
故答案为:乙.
14.解:当旋转到达地面时,为最短影长,等于AB,
∵最小值3m,
∴AB=3m,
∵影长最大时,木杆与光线垂直,
即AC=5m,
∴BC=4,
∵AE=5m,
∴EF=7.5m.
故答案为:7.5.
15.解:∵主视图和左视图都是长方形,
∴此几何体为柱体,
∵俯视图是一个圆,
∴此几何体为圆柱.
故答案为:圆柱.
三.解答题(共6小题,满分45分)
16.解:(1)如图所示:
;
(2)2×5×8+π×(2÷2)2×6
=80+π×1×6
=80+6π.
答:这个组合几何体的体积是80+6π.
17.解:如图:
18.解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∵AB=6m,BC=4m,EF=8
∴6:4=DE:8
∴DE=12(m).
19.解:
线段BC的长即为小赵的影子.
20.解:(1)如图所示:
汽车行驶到E点位置时,小明刚好看不到建筑物B;
(2)∵小明的视角为30°,A建筑物高25米,
∴AC=25,
∵∠AEC=45°,
∴AE=AC=25m,
∴ME=AM﹣AE=43.3﹣25=18.3m.
则他向前行驶了18.3米.
21.解:从它的正面、左面、上面三个方向所看到的平面图形(每个图(2分) )
常考题型达标测试题(附答案)
一.选择题(共10小题,满分50分)
1.下面四个几何体中,同一几何体从前往后看和从上往下看,看到的图形形状相同的共有( )几何体.
A.1个 B.2个 C.3个 D.4个
2.一个正三棱柱和一个正四棱柱的底面边长和高都相等,当一只小猫只看到它的一个侧面时,它看到( )
A.正三棱柱的区域大 B.正四棱柱的区域大
C.两者的区域一样大 D.无法确定
3.如图放置的几何体的左视图是( )
A. B. C. D.
4.用6个小立方块搭一个几何体,它主视图和俯视图如图所示,则它的左视图不可能是( )
A. B. C. D.
5.某几何体的主视图、左视图和俯视图分别如图所示,则该几何体的体积为( )
A.3π B.2π C.π D.12
6.观察如图所示的三种视图,与之对应的物体是( )
A. B. C. D.
7.如图为一个用正方体积木搭成的几何体的三视图,俯视图中方格上的数字表示该位置上积木累积的个数.若保证正视图和左视图成立,则a+b+c+d的最大值为( )
A.12 B.13 C.14 D.15
8.如图,是由一些完全相同的小正方体搭成的几何体的主视图和俯视图,则这个几何体的搭法有( )种.
A.3 B.4 C.5 D.6
9.要制作一个密封的长方体铁盒,嘉嘉设计出了它的三视图,如图,按图中尺寸(单位:cm)判断,要制作这个长方体铁盒,如果只考虑面积因素,采用下列哪种面积的铁板最合理( )
A.1000cm2 B.1030cm2 C.1100cm2 D.1200cm2
10.如图是某工件的三视图,则此工件的表面积为( )
A.20πcm2 B.36πcm2 C.56πcm2 D.24πcm2
二.填空题(共5小题,满分25分)
11.一个圆锥的主视图是底边为12,底边上的高为8的等腰三角形,则这个圆锥的表面积为 cm2.
12.太阳光形成的投影是 ,手电筒、电灯泡所发出的光线形成的投影是 .
13.一天上午小红先参加了校运动会女子100m比赛,过一段时间又参加了女子400m比赛,如图是摄影师在同一位置拍摄的两张照片,那么 (填“甲”或“乙”照片)是参加400m比赛时照的.
14.如图,一根直立于水平地面的木杆AB在灯光下形成影子AC(AC>AB),当木杆绕点A按逆时针方向旋转,直至到达地面时,影子的长度发生变化.已知AE=5m,在旋转过程中,影长的最大值为5m,最小值3m,且影长最大时,木杆与光线垂直,则路灯EF的高度为 m.
15.从三个不同方向看一个几何体,得到的平面图形如图所示,则这个几何体是 .
三.解答题(共6小题,满分45分)
16.如图①所示的组合几何体,它的下面是一个长方体,上面是一个圆柱.
(1)图②和图③是它的两个视图,在横线上分别填写两种视图的名称(填“主”、“左”或“俯”);
(2)根据两个视图中的尺寸,计算这个组合几何体的体积.(结果保留π)
17.平地上立着三根等高的木杆,其俯视图如图所示(图(1)(2)分别表示两个不同时刻的情况),图中画出了其中一根木杆在太阳光下的影子,请你在图中画出另外两根木杆在同一时刻的影子.
18.已知,AB和DE是直立在地面上的两根立柱,AB=6m,某一时刻AB在阳光下的投影BC=4m.
(1)请你在图中画出此时DE在阳光下的投影;
(2)在测量AB的投影时,同时测量出DE在阳光下的投影长为8m,请你计算DE的长.
19.如图,小赵和路人在路灯下行走,试确定图中路灯灯泡的位置,并画出小赵在灯光下的影子.
20.小明开着汽车在平坦的公路上行驶,前方出现两座建筑物A、B(如图),在(1)处小明能看到B建筑物的一部分,(如图),此时,小明的视角为30°,已知A建筑物高25米.
(1)请问汽车行驶到什么位置时,小明刚好看不到建筑物B?请在图中标出这点.
(2)若小明刚好看不到B建筑物时,他的视线与公路的夹角为45°,请问他向前行驶了多少米?( 精确到0.1)
21.先观察下图的立体图形,再分别画出从它的正面、左面、上面三个方向所看到的平面图形.
参考答案
一.选择题(共10小题,满分50分)
1.解:正方体从前往后看和从上往下看,看到的图形形状都是正方形,①符合题意;
球从前往后看和从上往下看,看到的图形形状都是圆,②符合题意;
圆锥从前往后看和从上往下看,看到的图形形状分别是三角形和圆,③不合题意;
圆柱从前往后看和从上往下看,看到的图形形状分别是矩形和圆,④不合题意,
故选:B.
2.解:正三棱柱和正四棱柱的底面边长和高相等,但是棱长不能确定,所以看到的区域大小不能确定.
故选:D.
3.解:左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
故选:C.
4.解:这样的几何体不止一种,而有多种摆法.
最少需要2+1+1+1=5(个)小立方块,最多需要2×3+1=7(个)小立方块.
因为用6个小立方块搭一个几何体,
所以它的左视图不可能是.
故选:D.
5.解:根据三视图可以判断该几何体为圆柱,圆柱的底面半径为1,高为3,
故体积为:πr2h=π×1×3=3π,
故选:A.
6.解:结合主视图和俯视图发现几何体的背面应该有个凸起,
故淘汰选项ABC,选D.
故选:D.
7.解:由正视图第1列和左视图第1列可知a最大为3,由正视图第2列和左视图第2列可知b最大为3,由正视图第3列和左视图第1列和第2列可知c最大为4,d最大为3,
则a+b+c+d的最大值为3+3+4+3=13.
故选:B.
8.解:由主视图易得这个几何体共有3层,由俯视图易得最底层有3个小正方体,第2列第二层和第3层的情况数有5种.
故选:C.
9.解:(18×12+18×10+12×10)×2
=(216+180+120)×2
=516×2
=1032(cm2),
故如果只考虑面积因素,采用面积1100cm2的铁板最合理.
故选:C.
10.解:由三视图,得:
OB=8÷2=4(cm),OA=3cm,
AB==5(cm),
圆锥的侧面积×8π×5=20π(cm2),
圆锥的底面积π×()2=16π(cm2),
圆锥的表面积20π+16π=36π(cm2).
故选:B.
二.填空题(共5小题,满分25分)
11.解:底面周长是12πcm,底面积是:π×(12÷2)2=36πcm2.
母线长是:=10cm,
则圆锥的侧面积是:π×(12÷2)×10=60πcm2,
则圆锥的表面积为36π+60π=96πcm2.
故答案是:96π.
12.解:∵由光线所形成的投影称为平行投影;有中心放射状光线所形成的投影称为中心投影.
∴太阳光形成的投影是平行投影,手电筒、电灯泡所发出的光线形成的投影是中心投影,
故答案为:平行投影,中心投影.
13.解:根据平行投影的规律:从早晨到傍晚物体的指向是:西﹣西北﹣北﹣东北﹣东,影长由长变短,再变长;
∵比赛是在上午进行,
∴则甲照片是参加100m的,乙照片是参加400m的.
故答案为:乙.
14.解:当旋转到达地面时,为最短影长,等于AB,
∵最小值3m,
∴AB=3m,
∵影长最大时,木杆与光线垂直,
即AC=5m,
∴BC=4,
∵AE=5m,
∴EF=7.5m.
故答案为:7.5.
15.解:∵主视图和左视图都是长方形,
∴此几何体为柱体,
∵俯视图是一个圆,
∴此几何体为圆柱.
故答案为:圆柱.
三.解答题(共6小题,满分45分)
16.解:(1)如图所示:
;
(2)2×5×8+π×(2÷2)2×6
=80+π×1×6
=80+6π.
答:这个组合几何体的体积是80+6π.
17.解:如图:
18.解:(1)连接AC,过点D作DF∥AC,交直线BC于点F,线段EF即为DE的投影.
(2)∵AC∥DF,
∴∠ACB=∠DFE.
∵∠ABC=∠DEF=90°
∵AB=6m,BC=4m,EF=8
∴6:4=DE:8
∴DE=12(m).
19.解:
线段BC的长即为小赵的影子.
20.解:(1)如图所示:
汽车行驶到E点位置时,小明刚好看不到建筑物B;
(2)∵小明的视角为30°,A建筑物高25米,
∴AC=25,
∵∠AEC=45°,
∴AE=AC=25m,
∴ME=AM﹣AE=43.3﹣25=18.3m.
则他向前行驶了18.3米.
21.解:从它的正面、左面、上面三个方向所看到的平面图形(每个图(2分) )
