2022-2023学年鲁教版(五四制)九年级数学上册 3.6二次函数的应用 题型分类练习题 (word版含答案)
文档属性
| 名称 | 2022-2023学年鲁教版(五四制)九年级数学上册 3.6二次函数的应用 题型分类练习题 (word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 599.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览




文档简介
2022-2023学年鲁教版九年级数学上册《3.6二次函数的应用》题型分类练习题(附答案)
一.实际问题到二次函数
1.据省统计局公布的数据,合肥市2021年一月GDP总值约为6百亿元人民币,若合肥市三月GDP总值为y百亿元人民币,平均每个月GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=6(1+2x) B.y=6(1﹣x)2
C.y=6(1+x)2 D.y=6+6(1+x)+6(1+x)2
2.商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x为正整数),每星期销售的利润为y元,则y与x的函数关系式为( )
A.y=10(200﹣10x) B.y=200(10+x)
C.y=10(200﹣10x)2 D.y=(10+x)(200﹣10x)
3.如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该农场计划用木材围成总长24m的栅栏,设面积为s(m2),垂直于墙的一边长为x(m).则s关于x的函数关系式: (并写出自变量的取值范围)
4.如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为( )
A.S=t(0<t≤3) B.S=t2(0<t≤3)
C.S=t2(0<t≤3) D.S=t2﹣1(0<t≤3)
二.课堂训练
5.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y平方米,则y关于x的函数关系式为( )
A.y=x(40﹣x) B.y=x(18﹣x)
C.y=x(40﹣2x) D.y=2x(40﹣2x)
6.一台机器原价100万元,若每年的折旧率是x,两年后这台机器约为y万元,则y与x的函数关系式为( )
A.y=100(1﹣x) B.y=100﹣x2
C.y=100(1+x)2 D.y=100(1﹣x)2
7.正方形边长为2,若边长增加x,那么面积增加y,则y与x的函数关系式是 .
8.某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量y(万件)与x之间的关系应表示为 .
三.能力提升
9.长方形的周长为12cm,其中一边为x(0<x<6)cm,面积为ycm2.那么y与x的关系是( )
A.y=(12﹣x)2 B.y=(6﹣x)2 C.y=x(12﹣x) D.y=x(6﹣x)
10.如图,某涵洞的截面是抛物线的一部分,现水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,求涵洞所在抛物线的解析式.
11.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系m=162﹣3x.
(1)请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到500元?如果能,求出此时的销售价格;如果不能,说明理由.
12.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
四.二次函数的应用
13.某幢建筑物,从10米高的窗口A用水管向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直),(如图)如果抛物线的最高点M离墙1米,离地面米,则水流下落点B离墙距离OB是( )
A.3米 B.2米 C.5米 D.4米
14.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
15.如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式h=﹣(t﹣6)2+5,则沙包在飞行过程中距离地面的最大高度是 米.
16.某产品进货单价为90元,按100元一件出售时,能售500件,如果这种商品每涨价1元,其销售量就减少10件,为了获得最大利润,其单价应定为 元.
五.课堂训练
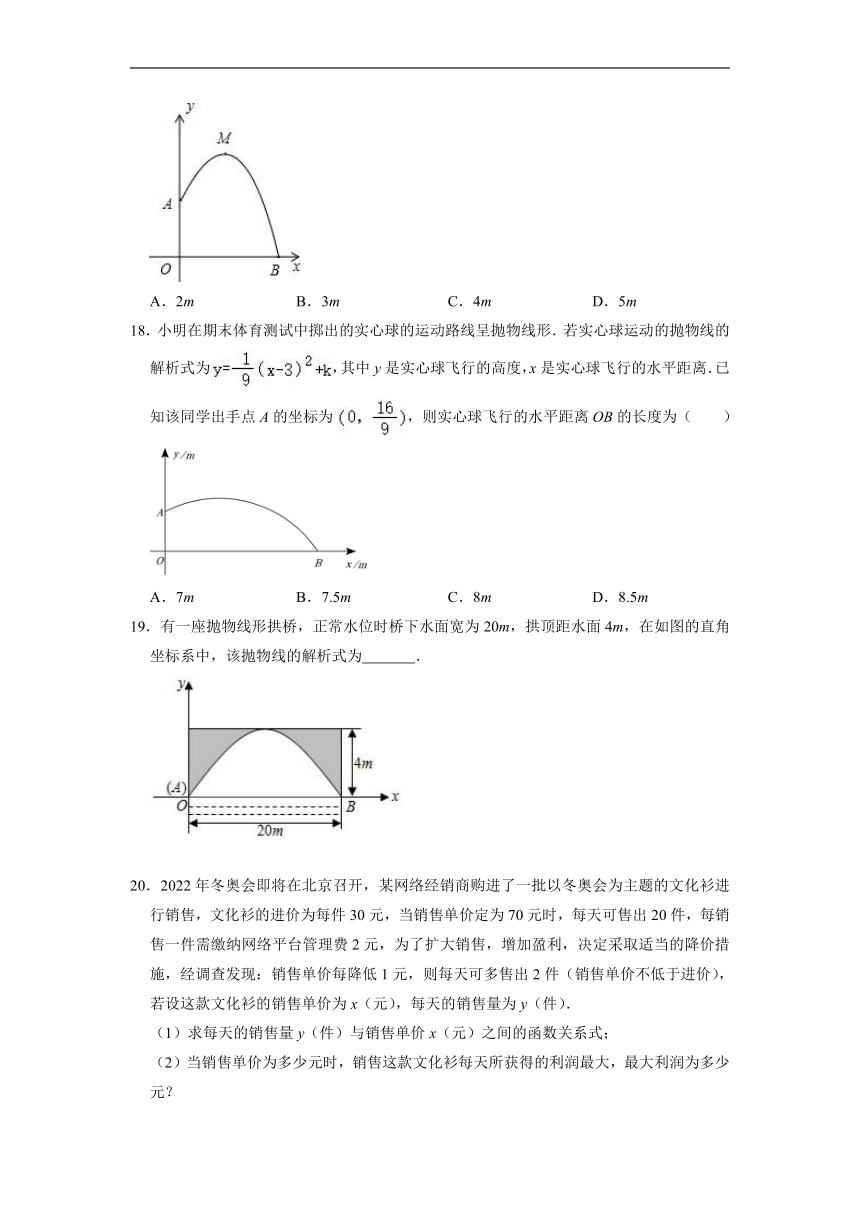
17.如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
18.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
19.有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m,在如图的直角坐标系中,该抛物线的解析式为 .
20.2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件30元,当销售单价定为70元时,每天可售出20件,每销售一件需缴纳网络平台管理费2元,为了扩大销售,增加盈利,决定采取适当的降价措施,经调查发现:销售单价每降低1元,则每天可多售出2件(销售单价不低于进价),若设这款文化衫的销售单价为x(元),每天的销售量为y(件).
(1)求每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?
六.能力提升
21.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是( )
A.柱子OA的高度为3m
B.喷出的水流距柱子1m处达到最大高度
C.喷出的水流距水平面的最大高度是3m
D.水池的半径至少要3m才能使喷出的水流不至于落在池外
22.某商品的进价为每件20元,售价为每件30元,每月可卖出180件.如果该商品的售价每上涨1元,就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数)时,月销售利润为y元.
(1)求y与x之间的函数解析式,并直接写出自变量x的取值范围.
(2)当每件商品的售价定为多少元时,可获得的月利润最大?最大月利润是多少?
23.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.
(1)求每次下降的百分率.
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
(3)在(2)的条件下,若使商场每天的盈利达到最大值,则应涨价多少元?此时每天的最大盈利是多少?
24.端午节吃粽子是中华民族的传统习俗,市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉棕和用6000元购进的豆沙粽盒数相同,在销售中,该商家发现猪肉棕每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒,设猪肉粽每盒售价x元,y表示该商家每天销售猪肉棕的利润(单位:元).
(1)猪肉棕和豆沙粽每盒的进价分别为 元和 元;
(2)若每盒利润率不超过50%,问猪肉粽价格为多少元时,商家每天获利1350元?
(3)若x满足50≤x≤65,求商家每天的最大利润.
七.二次函数的综合
25.如图,直线y1=﹣x+3与x轴于交于点B,与y轴交于点C.抛物线y2=﹣x2+bx+c经过B、C两点,并与x轴另一个交点为A.
(1)求抛物线y2的解析式;
(2)若点M在抛物线上,且S△MOC=4S△AOC,求点M的坐标;
(3)设点P是线段BC上一动点,过P作PQ⊥x轴,交抛物线于点Q,求线段PQ长度的最大值.
26.如图,在平面直角坐标系中,已知点B的坐标为(﹣2,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.
(1)求A,C两点的坐标;
(2)求抛物线的解析式;
(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.
27.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过点B、C,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在x轴上找一点E,使EC+ED的值最小,求EC+ED的最小值;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出P点坐标;若不存在,请说明理由.
28.如图,抛物线y=ax2+bx+4交x轴于点A(﹣1,0)、B(4,0),交y轴于点C,点P是直线BC上方抛物线上的一点.
(1)求抛物线的解析式;
(2)求△PBC的面积的最大值以及此时点P的坐标;
(3)在(2)的条件下,将直线BC向右平移个单位得到直线l,直线l交对称轴右侧的抛物线于点Q,连接PQ,点R为直线BC上的一动点,请问在在平面直角坐标系内是否存在一点T,使得四边形PQTR为菱形,若存在,请直接写出点T的坐标;若不存在,请说明理由.
八.课堂训练
29.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
30.如图,若一次函数y=﹣3x﹣3的图象与x轴、y轴分别交于A、C两点,点B的坐标为(3,0),二次函数y=ax2+bx﹣3的图象过A、B、C三点.
(1)求二次函数的表达式;
(2)如图1,若点P在直线BC下方的抛物线上运动,过P点作PF⊥BC,交线段BC于点F,在点P运动过程中,线段PF是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(3)点P在y轴右侧的抛物线上运动,过P点作x轴的垂线,与直线BC交于点D,若∠PCD+∠ACO=45°,请在备用图上画出示意图,并直接写出点P的坐标.
31.如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式;
(2)连接BC,求直线BC的解析式;
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值;
(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
32.如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象与y轴交于点C,与x轴交于点A、B,点A在原点的左侧,点A的坐标为(﹣1,0),点B的坐标为(3,0),且OB=OC.
(1)写出C点的坐标;
(2)求这个二次函数的解析式;
(3)若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,△AGP的面积最大?求此时点P的坐标和△AGP的最大面积.
九.能力提升
33.如图,已知二次函数y=ax2+bx+6的图象与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C.
(1)请求出该二次函数的表达式;
(2)请求出图象的对称轴和顶点坐标;
(3)在二次函数图象的对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
34.如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点坐标为C(3,6),并与y轴交于点B(0,3),点A是对称轴与x轴的交点.
(1)求抛物线的解析式;
(2)如图①所示,P是抛物线上的一个动点,且位于第一象限,连接BP,AP,求△ABP的面积的最大值;
(3)如图②所示,在对称轴AC的右侧作∠ACD=30°交抛物线于点D,求出D点的坐标;并探究:在y轴上是否存在点Q,使∠CQD=60°?若存在,求点Q的坐标;若不存在,请说明理由.
35.将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.
(1)求抛物线H的表达式;
(2)如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;
(3)如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
36.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A,B两点,与y轴交于点C,其中A(﹣1,0),B(4,0).
(1)求抛物线的解析式;
(2)连接BC,在直线BC上方的抛物线上有一动点D,连接AD,与直线BC相交于点E,当DE:AE=4:5时,求tan∠DAB的值;
(3)点P是直线BC上一点,在平面内是否存在点Q,使以点P,Q,C,A为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案
一.实际问题到二次函数
1.解:设平均每个月GDP增长的百分率为x,
由题意可得:
y关于x的函数表达式是:y=6(1+x)2,
故选:C.
2.解:由题意可得,y与x的函数关系式为:
y=(60﹣50+x)(200﹣10x)
=(10+x)(200﹣10x).
故选:D.
3.解:根据题意可知,三间羊圈与旧墙平行的一边的总长为(24﹣4x),
则:s=(24﹣4x)x=﹣4x2+24x
由图可知:24﹣4x>0,x>0,
所以x的取值范围是0<x<6,
故答案为:s=﹣4x2+24x(0<x<6).
4.解:如图所示,
∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=×OD×CD
=t2(0<t≤3),即S=t2(0<t≤3).故选:B.
二.课堂训练
5.解:设这个苗圃园垂直于墙的一边长为x米,则苗圃园与墙平行的一边长为(40﹣2x)米.
依题意可得:y=x(40﹣2x).
故选:C.
6.解:根据题意知y=100(1﹣x)2,
故选:D.
7.解:新正方形的边长为x+2,原正方形的边长为2.
∴新正方形的面积为(x+2)2,原正方形的面积为4,
∴y=(x+2)2﹣4=x2+4x,
故答案为y=x2+4x.
8.解:y与x之间的关系应表示为:y=20+20(x+1)+20(x+1)2.
故答案为:y=20+20(x+1)+20(x+1)2.
三.能力提升
9.解:∵长方形的周长为12cm,其中一边长为xcm,
∴另一边长为(6﹣x)cm,
面积y=x(6﹣x),
故选:D.
10.解:根据题意得:A(﹣0.8,﹣2.4),
设涵洞所在抛物线解析式为y=ax2,
把x=﹣0.8,y=﹣2.4代入得:a=﹣,
则涵洞所在抛物线解析式为y=﹣x2.
11.解:(1)由题意得,每件商品的销售利润为(x﹣30)元,那么m件的销售利润为y=m(x﹣30),
又∵m=162﹣3x,
∴y=(x﹣30)(162﹣3x),
即y=﹣3x2+252x﹣4860,
∵x﹣30≥0,
∴x≥30.
又∵m≥0,
∴162﹣3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=﹣3x2+252x﹣4860(30≤x≤54).
(2)由(1)得y=﹣3x2+252x﹣4860=﹣3(x﹣42)2+432,
所以可得售价定为42元时获得的利润最大,最大销售利润是432元.
∵500>432,
∴商场每天销售这种商品的销售利润不能达到500元.
12.解:∵PB=6﹣t,BE+EQ=6+t,
∴S=PB BQ=PB (BE+EQ)
=(6﹣t)(6+t)
=﹣t2+18,
∴S=﹣t2+18(0≤t<6).
四.二次函数的应用
13.解:以地面,墙面所在直线为x轴,y轴建立平面直角坐标系,
如图,
设抛物线解析式:y=a(x﹣1)2+,
把点A(0,10)代入抛物线解析式得:
a=﹣,
∴抛物线解析式:y=﹣(x﹣1)2+.
当y=0时,x1=﹣1(舍去),x2=3.
∴OB=3米.
故选:A.
14.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
15.解:∵h=﹣(t﹣6)2+5为开口向下的抛物线,
∴当t=6时,h最大=5.
故答案为:5.
16.解:设单价定为x,总利润为W,
则可得销量为:500﹣10(x﹣100),单件利润为:(x﹣90),
由题意得,W=(x﹣90)[500﹣10(x﹣100)]=﹣10x2+2400x﹣135000=﹣10(x﹣120)2+9000,
故可得,当x=120时,W取得最大,
即为了获得最大利润,其单价应定为120元.
故答案为:120.
五.课堂训练
17.解:设抛物线的解析式为y=a(x﹣1)2+,由题意,得
10=a+,
a=﹣.
∴抛物线的解析式为:y=﹣(x﹣1)2+.
当y=0时,
0=﹣(x﹣1)2+,
解得:x1=﹣1(舍去),x2=3.
OB=3m.
故选:B.
18.解:把A代入得:
=﹣×9+k,
∴k=,
∴y=﹣(x﹣3)2+,
令y=0得﹣(x﹣3)2+=0,
解得x=﹣2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故选:C.
19.解:(1)设所求抛物线的解析式为:y=a(x﹣h)2+k,
∵由AB=20,AB到拱桥顶C的距离为4m,
则C(10,4),A(0,0),B(20,0)
把A,B,C的坐标分别代入得a=﹣0.04,h=10,k=4
抛物线的解析式为y=﹣0.04(x﹣10)2+4.
故答案为:y=﹣0.04(x﹣10)2+4.
20.解:(1)由题意可得:y=20+2(70﹣x),
整理,得:y=﹣2x+160,
∴每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=﹣2x+160(30≤x<70);
(2)设销售所得利润为w,由题意可得:
w=(x﹣30﹣2)y=(x﹣32)(﹣2x+160)=﹣2x2+224x﹣5120,
整理,得:w=﹣2(x﹣56)2+1152,
∵﹣2<0,
∴当x=56时,w取最大值为1152,
∴当销售单价为56元时,销售这款文化衫每天所获得的利润最大,最大利润为1152元.
六.能力提升
21.解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴当x=0时,y=3,即OA=3m,故A选项正确,
当x=1时,y取得最大值,此时y=4,故B选项正确,C选项错误,
当y=0时,x=3或x=﹣1(舍去),故D选项正确,
故选:C.
22.解:(1)y=(30﹣20+x)(180﹣10x)=﹣10x2+80x+1800(0≤x≤5,且x为整数);
(2)由(1)知,y=﹣10x2+80x+1800(0≤x≤5,且x为整数).
∵﹣10<0,
∴当x==4时,y最大=1960元;
∴每件商品的售价为34元.
答:每件商品的售价为34元时,商品的利润最大,为1960元;
23.解:(1)设每次下降的百分率为a,根据题意,得:
50(1﹣a)2=32,
解得:a=1.8(舍)或a=0.2,
答:每次下降的百分率为20%;
(2)设每千克应涨价x元,由题意,得:
(10+x)(500﹣20x)=6000,
整理,得 x2﹣15x+50=0,
解得:x1=5,x2=10,
因为要尽快减少库存,所以x=5符合题意.
答:该商场要保证每天盈利6000元,那么每千克应涨价5元;
(3)设商场每天的盈利为y元,由(2)可知:
y=(10+x)(500﹣20x)=﹣20x2+300x+5000,
∵﹣20<0,
∴当x=﹣=7.5时,y取最大值,
∴当x=7.5时,y最大值=(10+7.5)×(500﹣20×7.5)=6125(元),
答:应涨价7.5元,每天的盈利达到最大值,为6125元.
24.解:(1)设猪肉粽每盒进价a元,则豆沙粽每盒进价(a﹣10)元,
则=,
解得a=40,
经检验a=40是方程的解,
∴猪肉粽每盒进价40元,豆沙粽每盒进价30元,
故答案为:40,30;
(2)∵每盒利润率不超过50%,
∴40≤x≤60,
由题意得,(x﹣40)[100﹣2(x﹣50)]=1350,
整理得,x2﹣140x+4675=0,
解得x1=85(舍去),x2=55.
答:猪肉粽价格为55元时,商家每天获利1350元;
(3)设商家的利润为y元,
∴y=x[100﹣2(x﹣50)]﹣40×[100﹣2(x﹣50)]=﹣2x2+280x﹣8000,
配方得:y=﹣2(x﹣70)2+1800,
∵x<70时,y随x的增大而增大,
∴当x=65时,y取最大值,最大值为1750.
答:最大利润为1750元.
七.二次函数的综合
25.解:(1)由直线y1=﹣x+3得:B(3,0),C(0,3),
将其代入y2=﹣x2+bx+c,得
.
解得.
故抛物线y2的解析式是:y2=﹣x2+2x+3;
(2)抛物线y2的解析式y2=﹣x2+2x+3=﹣(x﹣3)(x+1)知,A(﹣1,0).
∴OA=1.
又∵C(0,3),
∴OC=3.
设点M的坐标为(x,﹣x2+2x+3),
∵S△MOC=4S△AOC,
∴×3×|x|=4××3×1,
∴|x|=4,
∴x=±4,
当x=4时,﹣x2+2x+3=﹣16+8+3=﹣5;
当x=﹣4时,﹣x2+2x+3=﹣16﹣8+3=﹣21,
∴点M的坐标为(4,﹣5)或(﹣4,﹣21);
(3)设P(a,﹣a+3),此时Q(a,﹣a2+2a+3),
∴PQ=﹣a2+2a+3﹣(﹣a+3)=﹣a2+3a=﹣(a﹣)2+.
∴该抛物线顶点坐标是(,),且开口向下,
∴当a=时,PQ取最大值.
26.解:(1)∵B的坐标为(﹣2,0),
∴OB=2,
∴OA=OC=4OB=8,
故点A、C的坐标分别为(8,0)、(0,﹣8);
(2)由(1)知,抛物线的表达式可写为:y=a(x+2)(x﹣8)=a(x2﹣6x﹣16),
把C(0,﹣8)代入得:﹣16a=﹣8,
解得:a=,
故抛物线的表达式为:y=x2﹣3x﹣8;
(3)∵直线CA过点C,
∴设其函数表达式为:y=kx﹣8,
将点A坐标代入上式并解得:k=1,
故直线CA的表达式为:y=x﹣8,
过点P作y轴的平行线交AC于点H,
∵OA=OC=8,
∴∠OAC=∠OCA=45°,
∵PH∥y轴,
∴∠PHD=∠OCA=45°,
设点P(a,a2﹣3a﹣8),则点H(a,a﹣8),
∴PD=HPsin∠PHD=(a﹣8﹣a2+3a+8)==﹣(a﹣4)2+4,
∴当a=4时,其最大值为4,此时点P(4,﹣12).
27.解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0)、(0,3),
将点B、C的坐标代入二次函数表达式得:,解得:,
故函数的表达式为:y=﹣x2+2x+3,
令y=0,则x=﹣1或3,故点A(﹣1,0);
(2)如图1中,作点C关于x轴的对称点C′,连接CD′交x轴于点E,则此时EC+ED为最小,
函数顶点D坐标为(1,4),点C′(0,﹣3),
将C′、D的坐标代入一次函数表达式并解得:
直线C′D的表达式为:y=7x﹣3,
当y=0时,x=,
故点E(,0),
则EC+ED的最小值为DC′=;
(3)①当点P在x轴上方时,如图2中,
∵OB=OC=3,则∠OCB=45°=∠APB,
过点B作BH⊥AP于点H,设PH=BH=m,
则PB=PA=m,
由勾股定理得:AB2=AH2+BH2,
16=m2+(m﹣m)2,解得:m2=8+4,
则PB2=2m2=16+8
则yP==2+2;
②当点P在x轴下方时,
则yP=﹣(2);
故点P的坐标为(1,2)或(1,﹣2﹣2).
28.解:(1)将A(﹣1,0)、B(4,0)代入抛物线公式,如下:
,
求得.
抛物线解析式为:y=﹣x2+3x+4.
(2)设P到直线BC的距离为d,P点坐标为(x,﹣x2+3x+4)(0<x<4),
∵y=﹣x2+3x+4交y轴于点C,
令x=0,
∴y=4,
∴C(0,4),
由B(4,0),C(0,4)两点求得直线BC的解析式为:y+x﹣4=0.
作直线BC的平行线K:y=﹣x+m,因为K与BC平行,我们将K平移,根据题意,点P是直线BC上方抛物线上的一点,
∴随着K平行移动,以BC为底的△PBC的高d在逐渐增大,当K与抛物线y=﹣x2+3x+4恰有一个交点时,此时以BC为底的△PBC的高d最大,即此时△PBC面积最大.
∵此时K:y=﹣x+m与抛物线y=﹣x2+3x+4相交,且仅有一个交点,
∴﹣x+m=﹣x2+3x+4,m=8.
∴直线K:y=﹣x+8.
此时求K和抛物线的交点为:
﹣x+8=﹣x2+3x+4,解得x=2,
将x=2代入直线K:y=﹣x+8,
解得y=6.
因此P(2,6).
现在我们来求P到直线BC的距离,即△PBC的高d:
过P作垂直于BC的直线k:y=x+m.
∵P在直线k上,
∴6=2+m,
∴m=4,直线k=x+4.
直线K与直线k的交点为:,
解得交点坐标(0,4),即交点为C点.
因此的△PBC的高d即为B点和C点两点之间的距离,
∴d=|BC|==.
在△PBC中,
∵|BC|=4,△PBC的面积的最大值S△PBC=|BC| d==8.
(3)存在.直线BC向右平移个单位得到直线l,
∴l:y=﹣(x﹣)+4=﹣x+.
,解得.
二次函数y=﹣x2+3x+4对称轴为x=,
∵直线l交对称轴右侧的抛物线于点Q,
∴x=,代入y=﹣x+=.
∴Q().
设T(a,b).
∵R为直线BC上的一动点,∴设R(x,﹣x+4).
在菱形中PQTR中,|PR|=|QP|,
(2﹣x)2+([6﹣(﹣x+4)]2=(2﹣)2+(6﹣)2
解得x=±,
当x=时,点R的坐标(,4﹣),此时T点坐标为:T(+,﹣).
当x=﹣时,R(﹣,4+),此时T(﹣+,+)
综上所述:T存在两点,分别为:(+,﹣)或(﹣+,+).
八.课堂训练
29.解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
∴,
解得,
∴抛物线解析式为y=x2﹣4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=﹣x+3,
设点P(x,x2﹣4x+3),
∵PD∥y轴,
∴点D(x,﹣x+3),
∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣)2+,
∵a=﹣1<0,
∴当x=时,线段PD的长度有最大值;
(3)①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形.
30.解:(1)在y=﹣3x﹣3中,令x=0,得y=﹣3,
∴C(0,﹣3),
令y=0,得﹣3x﹣3=0,
解得:x=﹣1,
∴A(﹣1,0),
∵二次函数y=ax2+bx﹣3的图象过点A(﹣1,0),B(3,0),
∴,
解得:,
∴二次函数的表达式为:y=x2﹣2x﹣3;
(2)设直线BC的解析式为y=kx+c,
∵B(3,0),C(0,﹣3),
∴,
解得:,
∴直线BC的解析式为y=x﹣3,
在Rt△BOC中,OB=OC=3,BC===3,
设P(m,m2﹣2m﹣3),过点P作PT∥y轴交直线BC于点T,则T(m,m﹣3),
∴PT=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,
∵PF⊥BC,
∴∠PFT=∠BOC=90°,
∵PT∥y轴,
∴∠PTF=∠BCO,
∴△PTF∽△BCO,
∴=,即:=,
∴PF=(﹣m2+3m)=﹣(m﹣)2+,
∴当m=时,PF取得最大值;
(3)设P(t,t2﹣2t﹣3),分以下两种情况:
①当点P在直线BC下方的抛物线上时,如图2,过点P作PM⊥y轴于点M,
则M(0,t2﹣2t﹣3),
∴CM=t2﹣2t﹣3﹣(﹣3)=t2﹣2t,PM=t,
∵∠PCD+∠ACO=45°,∠BCO=45°,
∴∠ACP=90°,
∴∠PCM+∠ACO=∠CAO+∠ACO=90°,
∴∠PCM=∠CAO,
∵∠PMC=∠AOC=90°,
∴△PCM∽△CAO,
∴=,
∴=,
∴3t2﹣7t=0,
解得:t1=0(舍去),t2=,
当t=时,t2﹣2t﹣3=()2﹣2×﹣3=﹣,
∴P(,﹣);
②当点P在直线BC上方的抛物线上时,如图3,过点P作PM⊥y轴于点M,
则M(0,t2﹣2t﹣3),
∴CM=t2﹣2t﹣3﹣(﹣3)=t2﹣2t,PM=t,
∵∠PCD+∠ACO=45°,∠PCD+∠PCM=45°,
∴∠PCM=∠ACO,
∵∠PMC=∠AOC=90°,
∴△PCM∽△ACO,
∴=,
∴=,
∴t2﹣5t=0,
解得:t1=0(舍去),t2=5,
当t=5时,t2﹣2t﹣3=52﹣2×5﹣3=12,
∴P(5,12),
综上所述,点P的坐标为(,﹣)或(5,12).
31.解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,
解得,
∴y=﹣x2+3x+4;
(2)在y=﹣x2+3x+4中,令x=0,则y=4,
∴C(0,4),
设BC的解析式为y=kx+b,
∵B(4,0),C(0,4),
∴,
∴,
∴直线BC的解析式为y=﹣x+4.
(3)如图1中,
由题意A,B关于抛物线的对称轴直线x=对称,
连接BC交直线x=于点P,连接PA,此时PA+PC的值最小,最小值为线段BC的长==4,
此时P(,).
(4)如图2中,存在.
观察图象可知,满足条件的点N的纵坐标为4或﹣4,
对于抛物线y=﹣x2+3x+4,当y=4时,x2﹣3x=0,解得x=0或3,
∴N1(3,4).
当y=﹣4时,x2﹣3x﹣8=0,解得x=,
∴N2(,﹣4),N3(,﹣4),
综上所述,满足条件的点N的坐标为(3,4)或(,﹣4)或(,﹣4).
32.解:(1)由点B的坐标为(3,0),且OB=OC,得C(0,﹣3);
(2)二次函数y=ax2+bx+c(a>0)的图象过A、B、C点,得
,解得,
这个二次函数的解析式y=x2﹣2x﹣3;
(3)过点P作y轴的平行线与AG交于点Q,
当x=2时,y=22﹣2×2﹣3=﹣3,G(2,﹣3),
直线AG为y=﹣x﹣1.
设P(x,x2﹣2x﹣3),则Q(x,﹣x﹣1),
PQ=﹣x2+x+2.S△APG=S△APQ+S△GPQ=(﹣x2+x+2)×3
当x=时,△APG的面积最大,
此时P点的坐标为(,﹣),S△APG最大=××3=.
九.能力提升
33.解:(1)将A,B两点的坐标代入y=ax2+bx+6,得
.
解得.
∴二次函数的表达式为y=﹣x2+2x+6.
(2)∵y=﹣x2+2x+6=﹣(x﹣2)2+8,
∴二次函数图象的对称轴为直线x=2,顶点坐标为(2,8).
(3)存在,理由如下:
如图,作点C关于二次函数图象的对称轴的对称点C′,连接AC′,交二次函数图象的对称轴于点P,此时△APC的周长最小.
∵C(0,6),
∴C′(4,6).
设直线AC′的表达式为y=kx+n,则.
解得.
∴直线AC′的表达式为y=x+2.
当x=2时,y=4,即P(2,4).
34.解:(1)抛物线顶点坐标为C(3,6),
∴可设抛物线解析式为y=a(x﹣3)2+6,
将B(0,3)代入可得a=﹣,
∴y=﹣x2+2x+3;
(2)连接PO,
由题意,BO=3,AO=3,
设P(n,﹣n2+2n+3),
∴S△ABP=S△BOP+S△AOP﹣S△ABO,
S△BPO=n,
S△APO=﹣n2+3n+,
S△ABO=,
∴S△ABP=S△BOP+S△AOP﹣S△ABO=﹣n2+n=﹣(n﹣)2+,
∴当n=时,S△ABP的最大值为;
(3)存在,设D点的坐标为(t,﹣t2+2t+3),
过D作对称轴的垂线,垂足为G,
则DG=t﹣3,CG=6﹣(﹣t2+2t+3)=t2﹣2t+3,
∵∠ACD=30°,
∴2DG=DC,
在Rt△CGD中,
CG=DG,
∴(t﹣3)=t2﹣2t+3,
∴t=3+3或t=3(舍)
∴D(3+3,﹣3),
∴AG=3,GD=3,
连接AD,在Rt△ADG中,
∴AD==6,
∴AD=AC=6,∠CAD=120°,
∴在以A为圆心,AC为半径的圆与y轴的交点为Q点,
此时,∠CQD=∠CAD=60°,
设Q(0,m),AQ为圆A的半径,
AQ2=OA2+QO2=9+m2,
∴AQ2=AC2,
∴9+m2=36,
∴m=3或m=﹣3,
综上所述:Q点坐标为(0,3)或(0,﹣3).
35.解:(1)由题意得抛物线的顶点坐标为(﹣1,4),
∴抛物线H:y=a(x+1)2+4,
将A(﹣3,0)代入,得:a(﹣3+1)2+4=0,
解得:a=﹣1,
∴抛物线H的表达式为y=﹣(x+1)2+4;
(2)如图1,由(1)知:y=﹣x2﹣2x+3,
令x=0,得y=3,
∴C(0,3),
设直线AC的解析式为y=mx+n,
∵A(﹣3,0),C(0,3),
∴,
解得:,
∴直线AC的解析式为y=x+3,
设P(m,﹣m2﹣2m+3),则E(m,m+3),
∴PE=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m=﹣(m+)2+,
∵﹣1<0,
∴当m=﹣时,PE有最大值,
∵OA=OC=3,∠AOC=90°,
∴△AOC是等腰直角三角形,
∴∠ACO=45°,
∵PD⊥AB,
∴∠ADP=90°,
∴∠ADP=∠AOC,
∴PD∥OC,
∴∠PEF=∠ACO=45°,
∵PF⊥AC,
∴△PEF是等腰直角三角形,
∴PF=EF=PE,
∴S△PEF=PF EF=PE2,
∴当m=﹣时,S△PEF最大值=×()2=;
(3)①当AC为平行四边形的边时,则有PQ∥AC,且PQ=AC,
如图2,过点P作对称轴的垂线,垂足为G,设AC交对称轴于点H,
则∠AHG=∠ACO=∠PQG,
在△PQG和△ACO中,
,
∴△PQG≌△ACO(AAS),
∴PG=AO=3,
∴点P到对称轴的距离为3,
又∵y=﹣(x+1)2+4,
∴抛物线对称轴为直线x=﹣1,
设点P(x,y),则|x+1|=3,
解得:x=2或x=﹣4,
当x=2时,y=﹣5,
当x=﹣4时,y=﹣5,
∴点P坐标为(2,﹣5)或(﹣4,﹣5);
②当AC为平行四边形的对角线时,
如图3,设AC的中点为M,
∵A(﹣3,0),C(0,3),
∴M(﹣,),
∵点Q在对称轴上,
∴点Q的横坐标为﹣1,设点P的横坐标为x,
根据中点公式得:x+(﹣1)=2×(﹣)=﹣3,
∴x=﹣2,此时y=3,
∴P(﹣2,3);
综上所述,点P的坐标为(2,﹣5)或(﹣4,﹣5)或(﹣2,3).
36.解:将A(﹣1,0),B(4,0)代入y=ax2+bx+3,
得,解得,
∴解析式为;
(2)当x=0时,,
∴C(0,3),
设直线BC的解析式为y=kx+b,
将B(4,0),C(0,3)分别代入得,解得:,
∴直线BC的解析式为:,
过点D作y轴的平行线,交直线BC与点F,交x轴于点H,
过点A作y轴的平行线,交直线BC与点G,
∵A(﹣1,0),
∴当x=﹣1时,y=﹣=,
∴,,
∵AG∥y轴∥DF,
∴△DEF∽△AEG,
∴,
∴=,
∴DF=3,
设,,
∴,
解得:t1=t2=2,
∴,
∴,AH=1+2=3,
在Rt△ADH中,;
(3)存在,分三种情况:
①如图2,四边形ACPQ是菱形,则PC=AC,
设P(x,﹣x+3),
∵A(﹣1,0),C(0,3),
∴,
解得:x=,
当x=﹣时,P(﹣,),
∴Q(﹣﹣1,),
当x=时,P(,﹣),
∴Q(﹣1,﹣);
②如图3,四边形APCQ是菱形,
∵BC=AB=5,
∴B在AC的垂直平分线上,
∴P与B重合,
∴Q(﹣5,3);
③如图4,四边形ACQP是菱形,同理得P(,),
∴Q(,);
综上,点Q的坐标为(﹣﹣1,)或(﹣1,﹣)或(﹣5,3)或(,).
一.实际问题到二次函数
1.据省统计局公布的数据,合肥市2021年一月GDP总值约为6百亿元人民币,若合肥市三月GDP总值为y百亿元人民币,平均每个月GDP增长的百分率为x,则y关于x的函数表达式是( )
A.y=6(1+2x) B.y=6(1﹣x)2
C.y=6(1+x)2 D.y=6+6(1+x)+6(1+x)2
2.商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价上涨1元,则每星期就会少卖10件.每件商品的售价上涨x元(x为正整数),每星期销售的利润为y元,则y与x的函数关系式为( )
A.y=10(200﹣10x) B.y=200(10+x)
C.y=10(200﹣10x)2 D.y=(10+x)(200﹣10x)
3.如图,某农场要盖一排三间长方形的羊圈,打算一面利用旧墙,其余各面用木材围成栅栏,该农场计划用木材围成总长24m的栅栏,设面积为s(m2),垂直于墙的一边长为x(m).则s关于x的函数关系式: (并写出自变量的取值范围)
4.如图,在Rt△ABO中,AB⊥OB,且AB=OB=3,设直线x=t截此三角形所得的阴影部分的面积为S,则S与t之间的函数关系式为( )
A.S=t(0<t≤3) B.S=t2(0<t≤3)
C.S=t2(0<t≤3) D.S=t2﹣1(0<t≤3)
二.课堂训练
5.某中学课外兴趣活动小组准备围建一个矩形苗圃园,其中一边靠墙,另外三边用长为40米的篱笆围成,已知墙长为18米(如图所示),设这个苗圃园垂直于墙的一边长为x米,围成的苗圃面积为y平方米,则y关于x的函数关系式为( )
A.y=x(40﹣x) B.y=x(18﹣x)
C.y=x(40﹣2x) D.y=2x(40﹣2x)
6.一台机器原价100万元,若每年的折旧率是x,两年后这台机器约为y万元,则y与x的函数关系式为( )
A.y=100(1﹣x) B.y=100﹣x2
C.y=100(1+x)2 D.y=100(1﹣x)2
7.正方形边长为2,若边长增加x,那么面积增加y,则y与x的函数关系式是 .
8.某工厂今年一月份生产防疫护目镜的产量是20万件,计划之后两个月增加产量,如果月平均增长率为x,那么第一季度防疫护目镜的产量y(万件)与x之间的关系应表示为 .
三.能力提升
9.长方形的周长为12cm,其中一边为x(0<x<6)cm,面积为ycm2.那么y与x的关系是( )
A.y=(12﹣x)2 B.y=(6﹣x)2 C.y=x(12﹣x) D.y=x(6﹣x)
10.如图,某涵洞的截面是抛物线的一部分,现水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,求涵洞所在抛物线的解析式.
11.某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m(件)与每件的销售价x(元)满足一次函数关系m=162﹣3x.
(1)请写出商场卖这种商品每天的销售利润y(元)与每件销售价x(元)之间的函数关系式.
(2)商场每天销售这种商品的销售利润能否达到500元?如果能,求出此时的销售价格;如果不能,说明理由.
12.如图所示,在矩形ABCD中,AB=6厘米,BC=12厘米,点P在线段AB上,P从点A开始沿AB边以1厘米/秒的速度向点B移动.点E为线段BC的中点,点Q从E点开始,沿EC以1厘米/秒的速度向点C移动.如果P、Q同时分别从A、E出发,写出出发时间t与△BPQ的面积S的函数关系式,求出t的取值范围.
四.二次函数的应用
13.某幢建筑物,从10米高的窗口A用水管向外喷水,喷的水流呈抛物线(抛物线所在平面与墙面垂直),(如图)如果抛物线的最高点M离墙1米,离地面米,则水流下落点B离墙距离OB是( )
A.3米 B.2米 C.5米 D.4米
14.一人一盔安全守规,一人一带平安常在!某商店销售一批头盔,售价为每顶80元,每月可售出200顶.在“创建文明城市”期间,计划将头盔降价销售,经调查发现:每降价1元,每月可多售出20顶.已知头盔的进价为每顶50元,则该商店每月获得最大利润时,每顶头盔的售价为( )元.
A.60 B.65 C.70 D.75
15.如图,小明抛投一个沙包,沙包被抛出后距离地面的高度h(米)和飞行时间t(秒)近似满足函数关系式h=﹣(t﹣6)2+5,则沙包在飞行过程中距离地面的最大高度是 米.
16.某产品进货单价为90元,按100元一件出售时,能售500件,如果这种商品每涨价1元,其销售量就减少10件,为了获得最大利润,其单价应定为 元.
五.课堂训练
17.如图,从某建筑物10m高的窗口A处用水管向外喷水,喷出的水成抛物线状(抛物线所在平面与墙面垂直).如果抛物线的最高点M离墙1m,离地面m,则水流落地点B离墙的距离OB是( )
A.2m B.3m C.4m D.5m
18.小明在期末体育测试中掷出的实心球的运动路线呈抛物线形.若实心球运动的抛物线的解析式为,其中y是实心球飞行的高度,x是实心球飞行的水平距离.已知该同学出手点A的坐标为,则实心球飞行的水平距离OB的长度为( )
A.7m B.7.5m C.8m D.8.5m
19.有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m,在如图的直角坐标系中,该抛物线的解析式为 .
20.2022年冬奥会即将在北京召开,某网络经销商购进了一批以冬奥会为主题的文化衫进行销售,文化衫的进价为每件30元,当销售单价定为70元时,每天可售出20件,每销售一件需缴纳网络平台管理费2元,为了扩大销售,增加盈利,决定采取适当的降价措施,经调查发现:销售单价每降低1元,则每天可多售出2件(销售单价不低于进价),若设这款文化衫的销售单价为x(元),每天的销售量为y(件).
(1)求每天的销售量y(件)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少元时,销售这款文化衫每天所获得的利润最大,最大利润为多少元?
六.能力提升
21.某地要建造一个圆形喷水池,在水池中央垂直于地面安装一个柱子OA,O恰为水面中心,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下.在过OA的任一平面上,建立平面直角坐标系(如图),水流喷出的高度y(m)与水平距离x(m)之间的关系式是y=﹣x2+2x+3,则下列结论错误的是( )
A.柱子OA的高度为3m
B.喷出的水流距柱子1m处达到最大高度
C.喷出的水流距水平面的最大高度是3m
D.水池的半径至少要3m才能使喷出的水流不至于落在池外
22.某商品的进价为每件20元,售价为每件30元,每月可卖出180件.如果该商品的售价每上涨1元,就会少卖出10件,但每件售价不能高于35元,设每件商品的售价上涨x元(x为整数)时,月销售利润为y元.
(1)求y与x之间的函数解析式,并直接写出自变量x的取值范围.
(2)当每件商品的售价定为多少元时,可获得的月利润最大?最大月利润是多少?
23.某水果商场经销一种高档水果,原价每千克50元,连续两次降价后每千克32元,若每次下降的百分率相同.
(1)求每次下降的百分率.
(2)若每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下商场决定采取适当的涨价措施,若每千克涨价1元,日销售量将减少20千克,现该商场要保证每天盈利6000元,且要尽快减少库存,那么每千克应涨价多少元?
(3)在(2)的条件下,若使商场每天的盈利达到最大值,则应涨价多少元?此时每天的最大盈利是多少?
24.端午节吃粽子是中华民族的传统习俗,市场上豆沙粽的进价比猪肉粽的进价每盒便宜10元,某商家用8000元购进的猪肉棕和用6000元购进的豆沙粽盒数相同,在销售中,该商家发现猪肉棕每盒售价50元时,每天可售出100盒;每盒售价提高1元时,每天少售出2盒,设猪肉粽每盒售价x元,y表示该商家每天销售猪肉棕的利润(单位:元).
(1)猪肉棕和豆沙粽每盒的进价分别为 元和 元;
(2)若每盒利润率不超过50%,问猪肉粽价格为多少元时,商家每天获利1350元?
(3)若x满足50≤x≤65,求商家每天的最大利润.
七.二次函数的综合
25.如图,直线y1=﹣x+3与x轴于交于点B,与y轴交于点C.抛物线y2=﹣x2+bx+c经过B、C两点,并与x轴另一个交点为A.
(1)求抛物线y2的解析式;
(2)若点M在抛物线上,且S△MOC=4S△AOC,求点M的坐标;
(3)设点P是线段BC上一动点,过P作PQ⊥x轴,交抛物线于点Q,求线段PQ长度的最大值.
26.如图,在平面直角坐标系中,已知点B的坐标为(﹣2,0),且OA=OC=4OB,抛物线y=ax2+bx+c(a≠0)图象经过A,B,C三点.
(1)求A,C两点的坐标;
(2)求抛物线的解析式;
(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P的坐标及PD的最大值.
27.如图,直线y=﹣x+3与x轴、y轴分别交于B、C两点,抛物线y=﹣x2+bx+c经过点B、C,与x轴另一交点为A,顶点为D.
(1)求抛物线的解析式;
(2)在x轴上找一点E,使EC+ED的值最小,求EC+ED的最小值;
(3)在抛物线的对称轴上是否存在一点P,使得∠APB=∠OCB?若存在,求出P点坐标;若不存在,请说明理由.
28.如图,抛物线y=ax2+bx+4交x轴于点A(﹣1,0)、B(4,0),交y轴于点C,点P是直线BC上方抛物线上的一点.
(1)求抛物线的解析式;
(2)求△PBC的面积的最大值以及此时点P的坐标;
(3)在(2)的条件下,将直线BC向右平移个单位得到直线l,直线l交对称轴右侧的抛物线于点Q,连接PQ,点R为直线BC上的一动点,请问在在平面直角坐标系内是否存在一点T,使得四边形PQTR为菱形,若存在,请直接写出点T的坐标;若不存在,请说明理由.
八.课堂训练
29.如图,抛物线y=x2+bx+c过点A(3,0),B(1,0),交y轴于点C,点P是该抛物线上一动点,点P从C点沿抛物线向A点运动(点P不与A重合),过点P作PD∥y轴交直线AC于点D.
(1)求抛物线的解析式;
(2)求点P在运动的过程中线段PD长度的最大值;
(3)△APD能否构成直角三角形?若能,请直接写出所有符合条件的点P坐标;若不能,请说明理由.
30.如图,若一次函数y=﹣3x﹣3的图象与x轴、y轴分别交于A、C两点,点B的坐标为(3,0),二次函数y=ax2+bx﹣3的图象过A、B、C三点.
(1)求二次函数的表达式;
(2)如图1,若点P在直线BC下方的抛物线上运动,过P点作PF⊥BC,交线段BC于点F,在点P运动过程中,线段PF是否存在最大值?若存在,求出最大值;若不存在,请说明理由.
(3)点P在y轴右侧的抛物线上运动,过P点作x轴的垂线,与直线BC交于点D,若∠PCD+∠ACO=45°,请在备用图上画出示意图,并直接写出点P的坐标.
31.如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.
(1)求抛物线的解析式;
(2)连接BC,求直线BC的解析式;
(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值;
(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.
32.如图,在平面直角坐标系中,二次函数y=ax2+bx+c(a>0)的图象与y轴交于点C,与x轴交于点A、B,点A在原点的左侧,点A的坐标为(﹣1,0),点B的坐标为(3,0),且OB=OC.
(1)写出C点的坐标;
(2)求这个二次函数的解析式;
(3)若点G(2,y)是该抛物线上一点,点P是直线AG下方的抛物线上的一动点,当点P运动到什么位置时,△AGP的面积最大?求此时点P的坐标和△AGP的最大面积.
九.能力提升
33.如图,已知二次函数y=ax2+bx+6的图象与x轴交于A(﹣2,0),B(6,0)两点,与y轴交于点C.
(1)请求出该二次函数的表达式;
(2)请求出图象的对称轴和顶点坐标;
(3)在二次函数图象的对称轴上是否存在点P,使△APC的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由.
34.如图所示,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的顶点坐标为C(3,6),并与y轴交于点B(0,3),点A是对称轴与x轴的交点.
(1)求抛物线的解析式;
(2)如图①所示,P是抛物线上的一个动点,且位于第一象限,连接BP,AP,求△ABP的面积的最大值;
(3)如图②所示,在对称轴AC的右侧作∠ACD=30°交抛物线于点D,求出D点的坐标;并探究:在y轴上是否存在点Q,使∠CQD=60°?若存在,求点Q的坐标;若不存在,请说明理由.
35.将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.
(1)求抛物线H的表达式;
(2)如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;
(3)如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.
36.如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A,B两点,与y轴交于点C,其中A(﹣1,0),B(4,0).
(1)求抛物线的解析式;
(2)连接BC,在直线BC上方的抛物线上有一动点D,连接AD,与直线BC相交于点E,当DE:AE=4:5时,求tan∠DAB的值;
(3)点P是直线BC上一点,在平面内是否存在点Q,使以点P,Q,C,A为顶点的四边形是菱形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
参考答案
一.实际问题到二次函数
1.解:设平均每个月GDP增长的百分率为x,
由题意可得:
y关于x的函数表达式是:y=6(1+x)2,
故选:C.
2.解:由题意可得,y与x的函数关系式为:
y=(60﹣50+x)(200﹣10x)
=(10+x)(200﹣10x).
故选:D.
3.解:根据题意可知,三间羊圈与旧墙平行的一边的总长为(24﹣4x),
则:s=(24﹣4x)x=﹣4x2+24x
由图可知:24﹣4x>0,x>0,
所以x的取值范围是0<x<6,
故答案为:s=﹣4x2+24x(0<x<6).
4.解:如图所示,
∵Rt△AOB中,AB⊥OB,且AB=OB=3,
∴∠AOB=∠A=45°,
∵CD⊥OB,
∴CD∥AB,
∴∠OCD=∠A,
∴∠AOD=∠OCD=45°,
∴OD=CD=t,
∴S△OCD=×OD×CD
=t2(0<t≤3),即S=t2(0<t≤3).故选:B.
二.课堂训练
5.解:设这个苗圃园垂直于墙的一边长为x米,则苗圃园与墙平行的一边长为(40﹣2x)米.
依题意可得:y=x(40﹣2x).
故选:C.
6.解:根据题意知y=100(1﹣x)2,
故选:D.
7.解:新正方形的边长为x+2,原正方形的边长为2.
∴新正方形的面积为(x+2)2,原正方形的面积为4,
∴y=(x+2)2﹣4=x2+4x,
故答案为y=x2+4x.
8.解:y与x之间的关系应表示为:y=20+20(x+1)+20(x+1)2.
故答案为:y=20+20(x+1)+20(x+1)2.
三.能力提升
9.解:∵长方形的周长为12cm,其中一边长为xcm,
∴另一边长为(6﹣x)cm,
面积y=x(6﹣x),
故选:D.
10.解:根据题意得:A(﹣0.8,﹣2.4),
设涵洞所在抛物线解析式为y=ax2,
把x=﹣0.8,y=﹣2.4代入得:a=﹣,
则涵洞所在抛物线解析式为y=﹣x2.
11.解:(1)由题意得,每件商品的销售利润为(x﹣30)元,那么m件的销售利润为y=m(x﹣30),
又∵m=162﹣3x,
∴y=(x﹣30)(162﹣3x),
即y=﹣3x2+252x﹣4860,
∵x﹣30≥0,
∴x≥30.
又∵m≥0,
∴162﹣3x≥0,即x≤54.
∴30≤x≤54.
∴所求关系式为y=﹣3x2+252x﹣4860(30≤x≤54).
(2)由(1)得y=﹣3x2+252x﹣4860=﹣3(x﹣42)2+432,
所以可得售价定为42元时获得的利润最大,最大销售利润是432元.
∵500>432,
∴商场每天销售这种商品的销售利润不能达到500元.
12.解:∵PB=6﹣t,BE+EQ=6+t,
∴S=PB BQ=PB (BE+EQ)
=(6﹣t)(6+t)
=﹣t2+18,
∴S=﹣t2+18(0≤t<6).
四.二次函数的应用
13.解:以地面,墙面所在直线为x轴,y轴建立平面直角坐标系,
如图,
设抛物线解析式:y=a(x﹣1)2+,
把点A(0,10)代入抛物线解析式得:
a=﹣,
∴抛物线解析式:y=﹣(x﹣1)2+.
当y=0时,x1=﹣1(舍去),x2=3.
∴OB=3米.
故选:A.
14.解:每顶头盔降价x元,利润为w元,
由题意可得,w=(80﹣x﹣50)(200+20x)=﹣20(x﹣10)2+8000,
∴当x=10时,w取得最大值,此时80﹣x=70,
即该商店每月获得最大利润时,每顶头盔的售价为70元,
故选:C.
15.解:∵h=﹣(t﹣6)2+5为开口向下的抛物线,
∴当t=6时,h最大=5.
故答案为:5.
16.解:设单价定为x,总利润为W,
则可得销量为:500﹣10(x﹣100),单件利润为:(x﹣90),
由题意得,W=(x﹣90)[500﹣10(x﹣100)]=﹣10x2+2400x﹣135000=﹣10(x﹣120)2+9000,
故可得,当x=120时,W取得最大,
即为了获得最大利润,其单价应定为120元.
故答案为:120.
五.课堂训练
17.解:设抛物线的解析式为y=a(x﹣1)2+,由题意,得
10=a+,
a=﹣.
∴抛物线的解析式为:y=﹣(x﹣1)2+.
当y=0时,
0=﹣(x﹣1)2+,
解得:x1=﹣1(舍去),x2=3.
OB=3m.
故选:B.
18.解:把A代入得:
=﹣×9+k,
∴k=,
∴y=﹣(x﹣3)2+,
令y=0得﹣(x﹣3)2+=0,
解得x=﹣2(舍去)或x=8,
∴实心球飞行的水平距离OB的长度为8m,
故选:C.
19.解:(1)设所求抛物线的解析式为:y=a(x﹣h)2+k,
∵由AB=20,AB到拱桥顶C的距离为4m,
则C(10,4),A(0,0),B(20,0)
把A,B,C的坐标分别代入得a=﹣0.04,h=10,k=4
抛物线的解析式为y=﹣0.04(x﹣10)2+4.
故答案为:y=﹣0.04(x﹣10)2+4.
20.解:(1)由题意可得:y=20+2(70﹣x),
整理,得:y=﹣2x+160,
∴每天的销售量y(件)与销售单价x(元)之间的函数关系式为y=﹣2x+160(30≤x<70);
(2)设销售所得利润为w,由题意可得:
w=(x﹣30﹣2)y=(x﹣32)(﹣2x+160)=﹣2x2+224x﹣5120,
整理,得:w=﹣2(x﹣56)2+1152,
∵﹣2<0,
∴当x=56时,w取最大值为1152,
∴当销售单价为56元时,销售这款文化衫每天所获得的利润最大,最大利润为1152元.
六.能力提升
21.解:∵y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴当x=0时,y=3,即OA=3m,故A选项正确,
当x=1时,y取得最大值,此时y=4,故B选项正确,C选项错误,
当y=0时,x=3或x=﹣1(舍去),故D选项正确,
故选:C.
22.解:(1)y=(30﹣20+x)(180﹣10x)=﹣10x2+80x+1800(0≤x≤5,且x为整数);
(2)由(1)知,y=﹣10x2+80x+1800(0≤x≤5,且x为整数).
∵﹣10<0,
∴当x==4时,y最大=1960元;
∴每件商品的售价为34元.
答:每件商品的售价为34元时,商品的利润最大,为1960元;
23.解:(1)设每次下降的百分率为a,根据题意,得:
50(1﹣a)2=32,
解得:a=1.8(舍)或a=0.2,
答:每次下降的百分率为20%;
(2)设每千克应涨价x元,由题意,得:
(10+x)(500﹣20x)=6000,
整理,得 x2﹣15x+50=0,
解得:x1=5,x2=10,
因为要尽快减少库存,所以x=5符合题意.
答:该商场要保证每天盈利6000元,那么每千克应涨价5元;
(3)设商场每天的盈利为y元,由(2)可知:
y=(10+x)(500﹣20x)=﹣20x2+300x+5000,
∵﹣20<0,
∴当x=﹣=7.5时,y取最大值,
∴当x=7.5时,y最大值=(10+7.5)×(500﹣20×7.5)=6125(元),
答:应涨价7.5元,每天的盈利达到最大值,为6125元.
24.解:(1)设猪肉粽每盒进价a元,则豆沙粽每盒进价(a﹣10)元,
则=,
解得a=40,
经检验a=40是方程的解,
∴猪肉粽每盒进价40元,豆沙粽每盒进价30元,
故答案为:40,30;
(2)∵每盒利润率不超过50%,
∴40≤x≤60,
由题意得,(x﹣40)[100﹣2(x﹣50)]=1350,
整理得,x2﹣140x+4675=0,
解得x1=85(舍去),x2=55.
答:猪肉粽价格为55元时,商家每天获利1350元;
(3)设商家的利润为y元,
∴y=x[100﹣2(x﹣50)]﹣40×[100﹣2(x﹣50)]=﹣2x2+280x﹣8000,
配方得:y=﹣2(x﹣70)2+1800,
∵x<70时,y随x的增大而增大,
∴当x=65时,y取最大值,最大值为1750.
答:最大利润为1750元.
七.二次函数的综合
25.解:(1)由直线y1=﹣x+3得:B(3,0),C(0,3),
将其代入y2=﹣x2+bx+c,得
.
解得.
故抛物线y2的解析式是:y2=﹣x2+2x+3;
(2)抛物线y2的解析式y2=﹣x2+2x+3=﹣(x﹣3)(x+1)知,A(﹣1,0).
∴OA=1.
又∵C(0,3),
∴OC=3.
设点M的坐标为(x,﹣x2+2x+3),
∵S△MOC=4S△AOC,
∴×3×|x|=4××3×1,
∴|x|=4,
∴x=±4,
当x=4时,﹣x2+2x+3=﹣16+8+3=﹣5;
当x=﹣4时,﹣x2+2x+3=﹣16﹣8+3=﹣21,
∴点M的坐标为(4,﹣5)或(﹣4,﹣21);
(3)设P(a,﹣a+3),此时Q(a,﹣a2+2a+3),
∴PQ=﹣a2+2a+3﹣(﹣a+3)=﹣a2+3a=﹣(a﹣)2+.
∴该抛物线顶点坐标是(,),且开口向下,
∴当a=时,PQ取最大值.
26.解:(1)∵B的坐标为(﹣2,0),
∴OB=2,
∴OA=OC=4OB=8,
故点A、C的坐标分别为(8,0)、(0,﹣8);
(2)由(1)知,抛物线的表达式可写为:y=a(x+2)(x﹣8)=a(x2﹣6x﹣16),
把C(0,﹣8)代入得:﹣16a=﹣8,
解得:a=,
故抛物线的表达式为:y=x2﹣3x﹣8;
(3)∵直线CA过点C,
∴设其函数表达式为:y=kx﹣8,
将点A坐标代入上式并解得:k=1,
故直线CA的表达式为:y=x﹣8,
过点P作y轴的平行线交AC于点H,
∵OA=OC=8,
∴∠OAC=∠OCA=45°,
∵PH∥y轴,
∴∠PHD=∠OCA=45°,
设点P(a,a2﹣3a﹣8),则点H(a,a﹣8),
∴PD=HPsin∠PHD=(a﹣8﹣a2+3a+8)==﹣(a﹣4)2+4,
∴当a=4时,其最大值为4,此时点P(4,﹣12).
27.解:(1)直线y=﹣x+3与x轴、y轴分别交于B、C两点,则点B、C的坐标分别为(3,0)、(0,3),
将点B、C的坐标代入二次函数表达式得:,解得:,
故函数的表达式为:y=﹣x2+2x+3,
令y=0,则x=﹣1或3,故点A(﹣1,0);
(2)如图1中,作点C关于x轴的对称点C′,连接CD′交x轴于点E,则此时EC+ED为最小,
函数顶点D坐标为(1,4),点C′(0,﹣3),
将C′、D的坐标代入一次函数表达式并解得:
直线C′D的表达式为:y=7x﹣3,
当y=0时,x=,
故点E(,0),
则EC+ED的最小值为DC′=;
(3)①当点P在x轴上方时,如图2中,
∵OB=OC=3,则∠OCB=45°=∠APB,
过点B作BH⊥AP于点H,设PH=BH=m,
则PB=PA=m,
由勾股定理得:AB2=AH2+BH2,
16=m2+(m﹣m)2,解得:m2=8+4,
则PB2=2m2=16+8
则yP==2+2;
②当点P在x轴下方时,
则yP=﹣(2);
故点P的坐标为(1,2)或(1,﹣2﹣2).
28.解:(1)将A(﹣1,0)、B(4,0)代入抛物线公式,如下:
,
求得.
抛物线解析式为:y=﹣x2+3x+4.
(2)设P到直线BC的距离为d,P点坐标为(x,﹣x2+3x+4)(0<x<4),
∵y=﹣x2+3x+4交y轴于点C,
令x=0,
∴y=4,
∴C(0,4),
由B(4,0),C(0,4)两点求得直线BC的解析式为:y+x﹣4=0.
作直线BC的平行线K:y=﹣x+m,因为K与BC平行,我们将K平移,根据题意,点P是直线BC上方抛物线上的一点,
∴随着K平行移动,以BC为底的△PBC的高d在逐渐增大,当K与抛物线y=﹣x2+3x+4恰有一个交点时,此时以BC为底的△PBC的高d最大,即此时△PBC面积最大.
∵此时K:y=﹣x+m与抛物线y=﹣x2+3x+4相交,且仅有一个交点,
∴﹣x+m=﹣x2+3x+4,m=8.
∴直线K:y=﹣x+8.
此时求K和抛物线的交点为:
﹣x+8=﹣x2+3x+4,解得x=2,
将x=2代入直线K:y=﹣x+8,
解得y=6.
因此P(2,6).
现在我们来求P到直线BC的距离,即△PBC的高d:
过P作垂直于BC的直线k:y=x+m.
∵P在直线k上,
∴6=2+m,
∴m=4,直线k=x+4.
直线K与直线k的交点为:,
解得交点坐标(0,4),即交点为C点.
因此的△PBC的高d即为B点和C点两点之间的距离,
∴d=|BC|==.
在△PBC中,
∵|BC|=4,△PBC的面积的最大值S△PBC=|BC| d==8.
(3)存在.直线BC向右平移个单位得到直线l,
∴l:y=﹣(x﹣)+4=﹣x+.
,解得.
二次函数y=﹣x2+3x+4对称轴为x=,
∵直线l交对称轴右侧的抛物线于点Q,
∴x=,代入y=﹣x+=.
∴Q().
设T(a,b).
∵R为直线BC上的一动点,∴设R(x,﹣x+4).
在菱形中PQTR中,|PR|=|QP|,
(2﹣x)2+([6﹣(﹣x+4)]2=(2﹣)2+(6﹣)2
解得x=±,
当x=时,点R的坐标(,4﹣),此时T点坐标为:T(+,﹣).
当x=﹣时,R(﹣,4+),此时T(﹣+,+)
综上所述:T存在两点,分别为:(+,﹣)或(﹣+,+).
八.课堂训练
29.解:(1)∵抛物线y=x2+bx+c过点A(3,0),B(1,0),
∴,
解得,
∴抛物线解析式为y=x2﹣4x+3;
(2)令x=0,则y=3,
∴点C(0,3),
则直线AC的解析式为y=﹣x+3,
设点P(x,x2﹣4x+3),
∵PD∥y轴,
∴点D(x,﹣x+3),
∴PD=(﹣x+3)﹣(x2﹣4x+3)=﹣x2+3x=﹣(x﹣)2+,
∵a=﹣1<0,
∴当x=时,线段PD的长度有最大值;
(3)①∠APD是直角时,点P与点B重合,
此时,点P(1,0),
②∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴抛物线的顶点坐标为(2,﹣1),
∵A(3,0),
∴点P为在抛物线顶点时,∠PAD=45°+45°=90°,
此时,点P(2,﹣1),
综上所述,点P(1,0)或(2,﹣1)时,△APD能构成直角三角形.
30.解:(1)在y=﹣3x﹣3中,令x=0,得y=﹣3,
∴C(0,﹣3),
令y=0,得﹣3x﹣3=0,
解得:x=﹣1,
∴A(﹣1,0),
∵二次函数y=ax2+bx﹣3的图象过点A(﹣1,0),B(3,0),
∴,
解得:,
∴二次函数的表达式为:y=x2﹣2x﹣3;
(2)设直线BC的解析式为y=kx+c,
∵B(3,0),C(0,﹣3),
∴,
解得:,
∴直线BC的解析式为y=x﹣3,
在Rt△BOC中,OB=OC=3,BC===3,
设P(m,m2﹣2m﹣3),过点P作PT∥y轴交直线BC于点T,则T(m,m﹣3),
∴PT=m﹣3﹣(m2﹣2m﹣3)=﹣m2+3m,
∵PF⊥BC,
∴∠PFT=∠BOC=90°,
∵PT∥y轴,
∴∠PTF=∠BCO,
∴△PTF∽△BCO,
∴=,即:=,
∴PF=(﹣m2+3m)=﹣(m﹣)2+,
∴当m=时,PF取得最大值;
(3)设P(t,t2﹣2t﹣3),分以下两种情况:
①当点P在直线BC下方的抛物线上时,如图2,过点P作PM⊥y轴于点M,
则M(0,t2﹣2t﹣3),
∴CM=t2﹣2t﹣3﹣(﹣3)=t2﹣2t,PM=t,
∵∠PCD+∠ACO=45°,∠BCO=45°,
∴∠ACP=90°,
∴∠PCM+∠ACO=∠CAO+∠ACO=90°,
∴∠PCM=∠CAO,
∵∠PMC=∠AOC=90°,
∴△PCM∽△CAO,
∴=,
∴=,
∴3t2﹣7t=0,
解得:t1=0(舍去),t2=,
当t=时,t2﹣2t﹣3=()2﹣2×﹣3=﹣,
∴P(,﹣);
②当点P在直线BC上方的抛物线上时,如图3,过点P作PM⊥y轴于点M,
则M(0,t2﹣2t﹣3),
∴CM=t2﹣2t﹣3﹣(﹣3)=t2﹣2t,PM=t,
∵∠PCD+∠ACO=45°,∠PCD+∠PCM=45°,
∴∠PCM=∠ACO,
∵∠PMC=∠AOC=90°,
∴△PCM∽△ACO,
∴=,
∴=,
∴t2﹣5t=0,
解得:t1=0(舍去),t2=5,
当t=5时,t2﹣2t﹣3=52﹣2×5﹣3=12,
∴P(5,12),
综上所述,点P的坐标为(,﹣)或(5,12).
31.解:(1)把A(﹣1,0),B(4,0)代入y=ax2+bx+4,得到,
解得,
∴y=﹣x2+3x+4;
(2)在y=﹣x2+3x+4中,令x=0,则y=4,
∴C(0,4),
设BC的解析式为y=kx+b,
∵B(4,0),C(0,4),
∴,
∴,
∴直线BC的解析式为y=﹣x+4.
(3)如图1中,
由题意A,B关于抛物线的对称轴直线x=对称,
连接BC交直线x=于点P,连接PA,此时PA+PC的值最小,最小值为线段BC的长==4,
此时P(,).
(4)如图2中,存在.
观察图象可知,满足条件的点N的纵坐标为4或﹣4,
对于抛物线y=﹣x2+3x+4,当y=4时,x2﹣3x=0,解得x=0或3,
∴N1(3,4).
当y=﹣4时,x2﹣3x﹣8=0,解得x=,
∴N2(,﹣4),N3(,﹣4),
综上所述,满足条件的点N的坐标为(3,4)或(,﹣4)或(,﹣4).
32.解:(1)由点B的坐标为(3,0),且OB=OC,得C(0,﹣3);
(2)二次函数y=ax2+bx+c(a>0)的图象过A、B、C点,得
,解得,
这个二次函数的解析式y=x2﹣2x﹣3;
(3)过点P作y轴的平行线与AG交于点Q,
当x=2时,y=22﹣2×2﹣3=﹣3,G(2,﹣3),
直线AG为y=﹣x﹣1.
设P(x,x2﹣2x﹣3),则Q(x,﹣x﹣1),
PQ=﹣x2+x+2.S△APG=S△APQ+S△GPQ=(﹣x2+x+2)×3
当x=时,△APG的面积最大,
此时P点的坐标为(,﹣),S△APG最大=××3=.
九.能力提升
33.解:(1)将A,B两点的坐标代入y=ax2+bx+6,得
.
解得.
∴二次函数的表达式为y=﹣x2+2x+6.
(2)∵y=﹣x2+2x+6=﹣(x﹣2)2+8,
∴二次函数图象的对称轴为直线x=2,顶点坐标为(2,8).
(3)存在,理由如下:
如图,作点C关于二次函数图象的对称轴的对称点C′,连接AC′,交二次函数图象的对称轴于点P,此时△APC的周长最小.
∵C(0,6),
∴C′(4,6).
设直线AC′的表达式为y=kx+n,则.
解得.
∴直线AC′的表达式为y=x+2.
当x=2时,y=4,即P(2,4).
34.解:(1)抛物线顶点坐标为C(3,6),
∴可设抛物线解析式为y=a(x﹣3)2+6,
将B(0,3)代入可得a=﹣,
∴y=﹣x2+2x+3;
(2)连接PO,
由题意,BO=3,AO=3,
设P(n,﹣n2+2n+3),
∴S△ABP=S△BOP+S△AOP﹣S△ABO,
S△BPO=n,
S△APO=﹣n2+3n+,
S△ABO=,
∴S△ABP=S△BOP+S△AOP﹣S△ABO=﹣n2+n=﹣(n﹣)2+,
∴当n=时,S△ABP的最大值为;
(3)存在,设D点的坐标为(t,﹣t2+2t+3),
过D作对称轴的垂线,垂足为G,
则DG=t﹣3,CG=6﹣(﹣t2+2t+3)=t2﹣2t+3,
∵∠ACD=30°,
∴2DG=DC,
在Rt△CGD中,
CG=DG,
∴(t﹣3)=t2﹣2t+3,
∴t=3+3或t=3(舍)
∴D(3+3,﹣3),
∴AG=3,GD=3,
连接AD,在Rt△ADG中,
∴AD==6,
∴AD=AC=6,∠CAD=120°,
∴在以A为圆心,AC为半径的圆与y轴的交点为Q点,
此时,∠CQD=∠CAD=60°,
设Q(0,m),AQ为圆A的半径,
AQ2=OA2+QO2=9+m2,
∴AQ2=AC2,
∴9+m2=36,
∴m=3或m=﹣3,
综上所述:Q点坐标为(0,3)或(0,﹣3).
35.解:(1)由题意得抛物线的顶点坐标为(﹣1,4),
∴抛物线H:y=a(x+1)2+4,
将A(﹣3,0)代入,得:a(﹣3+1)2+4=0,
解得:a=﹣1,
∴抛物线H的表达式为y=﹣(x+1)2+4;
(2)如图1,由(1)知:y=﹣x2﹣2x+3,
令x=0,得y=3,
∴C(0,3),
设直线AC的解析式为y=mx+n,
∵A(﹣3,0),C(0,3),
∴,
解得:,
∴直线AC的解析式为y=x+3,
设P(m,﹣m2﹣2m+3),则E(m,m+3),
∴PE=﹣m2﹣2m+3﹣(m+3)=﹣m2﹣3m=﹣(m+)2+,
∵﹣1<0,
∴当m=﹣时,PE有最大值,
∵OA=OC=3,∠AOC=90°,
∴△AOC是等腰直角三角形,
∴∠ACO=45°,
∵PD⊥AB,
∴∠ADP=90°,
∴∠ADP=∠AOC,
∴PD∥OC,
∴∠PEF=∠ACO=45°,
∵PF⊥AC,
∴△PEF是等腰直角三角形,
∴PF=EF=PE,
∴S△PEF=PF EF=PE2,
∴当m=﹣时,S△PEF最大值=×()2=;
(3)①当AC为平行四边形的边时,则有PQ∥AC,且PQ=AC,
如图2,过点P作对称轴的垂线,垂足为G,设AC交对称轴于点H,
则∠AHG=∠ACO=∠PQG,
在△PQG和△ACO中,
,
∴△PQG≌△ACO(AAS),
∴PG=AO=3,
∴点P到对称轴的距离为3,
又∵y=﹣(x+1)2+4,
∴抛物线对称轴为直线x=﹣1,
设点P(x,y),则|x+1|=3,
解得:x=2或x=﹣4,
当x=2时,y=﹣5,
当x=﹣4时,y=﹣5,
∴点P坐标为(2,﹣5)或(﹣4,﹣5);
②当AC为平行四边形的对角线时,
如图3,设AC的中点为M,
∵A(﹣3,0),C(0,3),
∴M(﹣,),
∵点Q在对称轴上,
∴点Q的横坐标为﹣1,设点P的横坐标为x,
根据中点公式得:x+(﹣1)=2×(﹣)=﹣3,
∴x=﹣2,此时y=3,
∴P(﹣2,3);
综上所述,点P的坐标为(2,﹣5)或(﹣4,﹣5)或(﹣2,3).
36.解:将A(﹣1,0),B(4,0)代入y=ax2+bx+3,
得,解得,
∴解析式为;
(2)当x=0时,,
∴C(0,3),
设直线BC的解析式为y=kx+b,
将B(4,0),C(0,3)分别代入得,解得:,
∴直线BC的解析式为:,
过点D作y轴的平行线,交直线BC与点F,交x轴于点H,
过点A作y轴的平行线,交直线BC与点G,
∵A(﹣1,0),
∴当x=﹣1时,y=﹣=,
∴,,
∵AG∥y轴∥DF,
∴△DEF∽△AEG,
∴,
∴=,
∴DF=3,
设,,
∴,
解得:t1=t2=2,
∴,
∴,AH=1+2=3,
在Rt△ADH中,;
(3)存在,分三种情况:
①如图2,四边形ACPQ是菱形,则PC=AC,
设P(x,﹣x+3),
∵A(﹣1,0),C(0,3),
∴,
解得:x=,
当x=﹣时,P(﹣,),
∴Q(﹣﹣1,),
当x=时,P(,﹣),
∴Q(﹣1,﹣);
②如图3,四边形APCQ是菱形,
∵BC=AB=5,
∴B在AC的垂直平分线上,
∴P与B重合,
∴Q(﹣5,3);
③如图4,四边形ACQP是菱形,同理得P(,),
∴Q(,);
综上,点Q的坐标为(﹣﹣1,)或(﹣1,﹣)或(﹣5,3)或(,).
