河北省沧州市孟村回族自治县2021-2022学年八年级上学期期末数学试题(word版含简略答案)
文档属性
| 名称 | 河北省沧州市孟村回族自治县2021-2022学年八年级上学期期末数学试题(word版含简略答案) |  | |
| 格式 | docx | ||
| 文件大小 | 499.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-05 16:22:12 | ||
图片预览


文档简介
2021~2022学年八年级第一学期期末考试
数学(人教版)
一、选择题.(本题共有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题所给四个选项中,只有一项符合题目要求)
1. 将一张长方形纸对折,然后用笔尖在纸上扎出“B”,再把纸铺平,可以看到的是( )
A. B. C. D.
2. 某公司运用5G技术,下载一个2.4M的文件大约只需要0.000048秒,则0.000048用科学记数法表示为( )
A. B. C. D.
3. 下列选项是最简分式的是( )
A. B. C. D.
4. 将多项式利用提公因式法分解因式,则提取的公因式为( )
A. B. ab C. a D. b
5. 在平面直角坐标系中,点A(m+1,5)与点B(3,n)关于y轴对称,则m,n的值分别为( )
A. m=-4,n=5 B. m=-4,n=3 C. m=2,n=5 D. m=-2,n=5
6. 如图,将一张含有角三角形纸片的两个顶点叠放在长方形纸条的两条对边上,若,则的度数为( )
A. B. C. D.
7. 如图,已知Rt△ABD≌Rt△CDB,则∠ADB+∠C=( )
A. 70° B. 80° C. 90° D. 无法确定
8. 已知,,则a与b的大小关系为( )
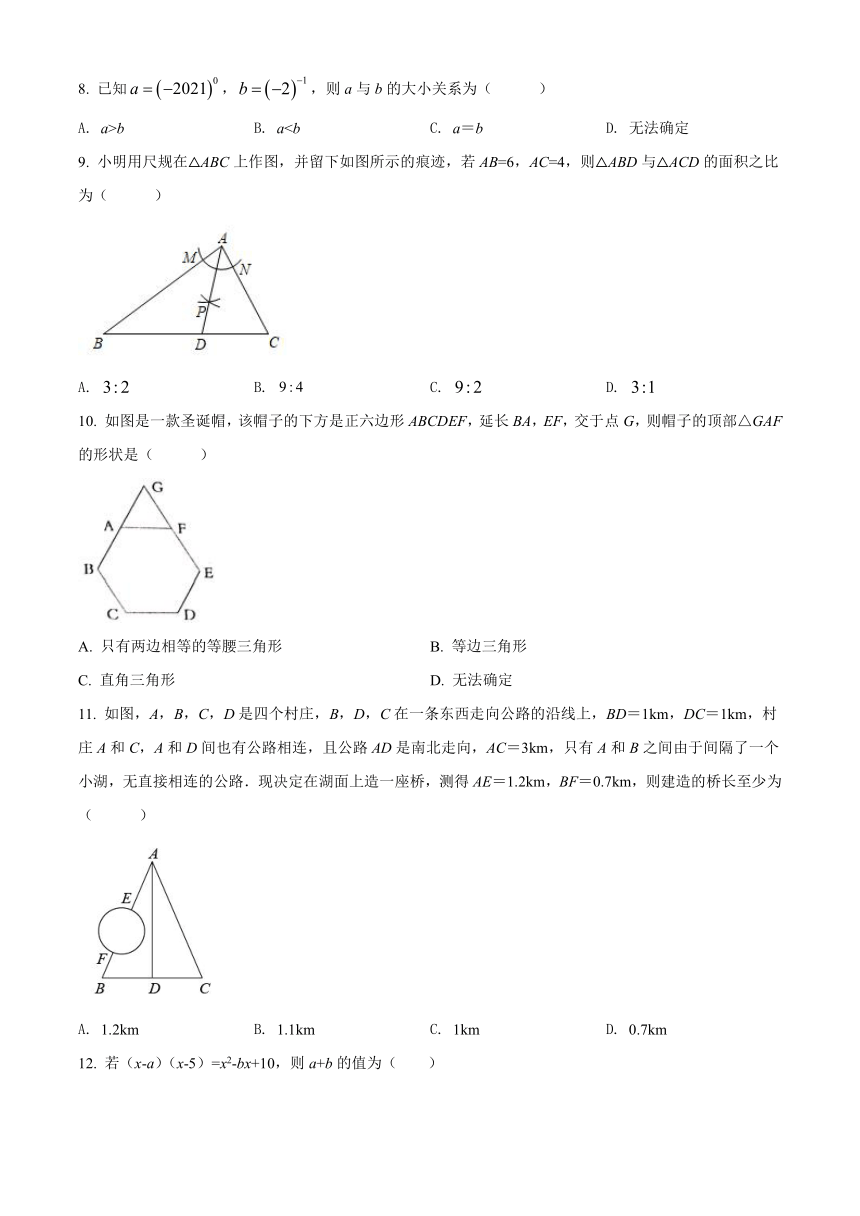
A. a>b B. a9. 小明用尺规在△ABC上作图,并留下如图所示的痕迹,若AB=6,AC=4,则△ABD与△ACD的面积之比为( )
A. B. C. D.
10. 如图是一款圣诞帽,该帽子的下方是正六边形ABCDEF,延长BA,EF,交于点G,则帽子的顶部△GAF的形状是( )
A. 只有两边相等的等腰三角形 B. 等边三角形
C. 直角三角形 D. 无法确定
11. 如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄A和C,A和D间也有公路相连,且公路AD是南北走向,AC=3km,只有A和B之间由于间隔了一个小湖,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,BF=0.7km,则建造的桥长至少为( )
A. 1.2km B. 1.1km C. 1km D. 0.7km
12. 若(x-a)(x-5)=x2-bx+10,则a+b的值为( )
A 2 B. 5 C. 7 D. 9
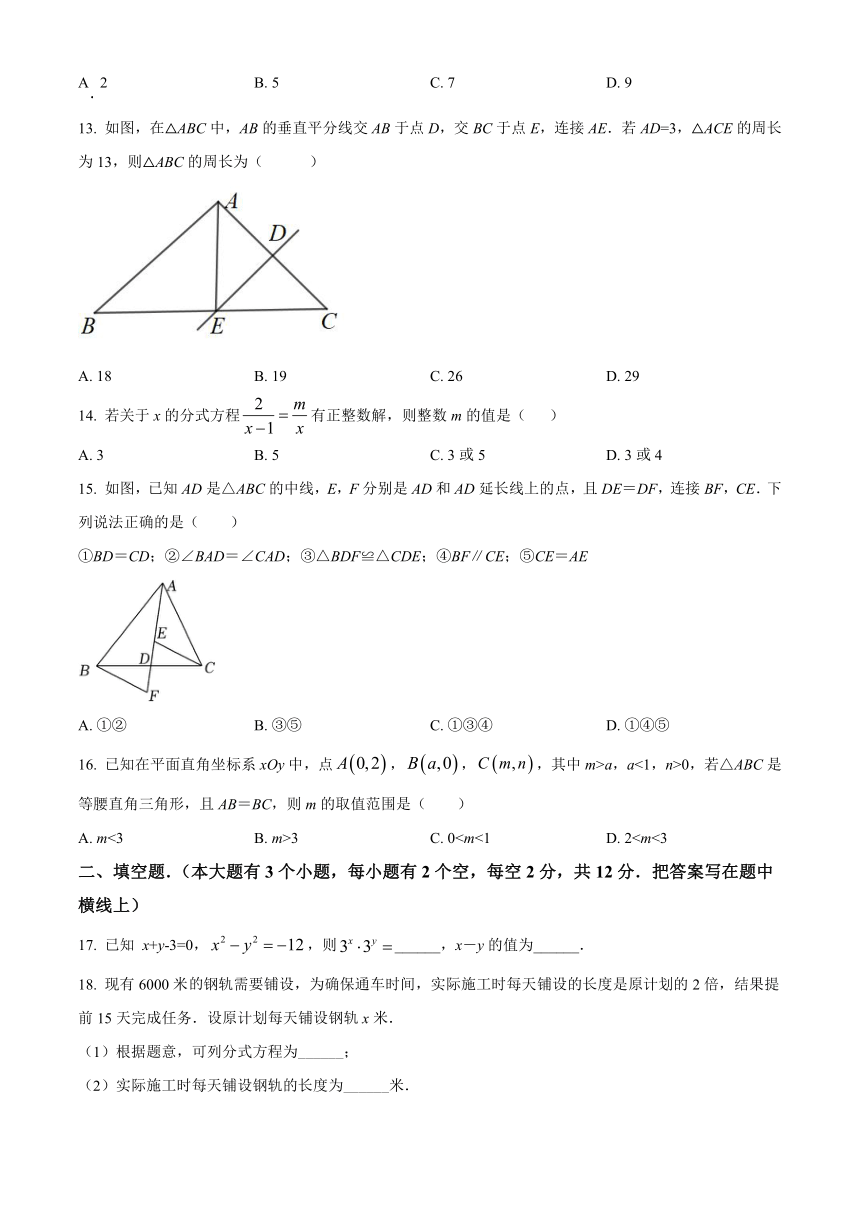
13. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若AD=3,△ACE的周长为13,则△ABC的周长为( )
A. 18 B. 19 C. 26 D. 29
14. 若关于x的分式方程有正整数解,则整数m的值是( )
A. 3 B. 5 C. 3或5 D. 3或4
15. 如图,已知AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法正确的是( )
①BD=CD;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
16. 已知在平面直角坐标系xOy中,点,,,其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A. m<3 B. m>3 C. 0二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
17. 已知 x+y-3=0,,则______,x-y的值为______.
18. 现有6000米钢轨需要铺设,为确保通车时间,实际施工时每天铺设的长度是原计划的2倍,结果提前15天完成任务.设原计划每天铺设钢轨x米.
(1)根据题意,可列分式方程为______;
(2)实际施工时每天铺设钢轨的长度为______米.
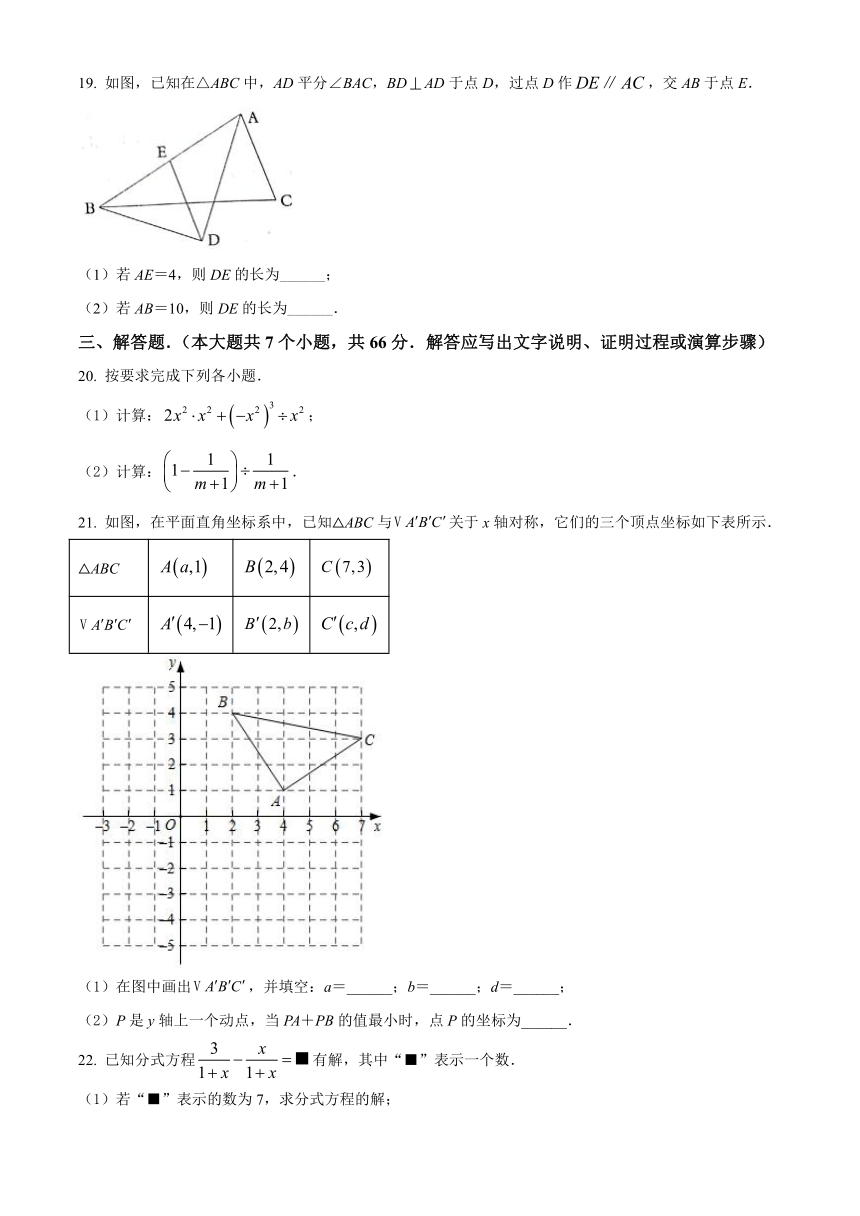
19. 如图,已知在△ABC中,AD平分∠BAC,BDAD于点D,过点D作,交AB于点E.
(1)若AE=4,则DE的长为______;
(2)若AB=10,则DE的长为______.
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20. 按要求完成下列各小题.
(1)计算:;
(2)计算:.
21. 如图,在平面直角坐标系中,已知△ABC与关于x轴对称,它们的三个顶点坐标如下表所示.
△ABC
(1)在图中画出,并填空:a=______;b=______;d=______;
(2)P是y轴上一个动点,当PA+PB的值最小时,点P的坐标为______.
22. 已知分式方程有解,其中“■”表示一个数.
(1)若“■”表示的数为7,求分式方程的解;
(2)嘉淇回忆说:由于抄题时等号右边的数值抄错,导致找不到原题目,但可以肯定的是“■”是-1或0,试确定“■”表示的数.
23 阅读材料:将(x+y)2+2(x+y)+1分解因式.
解:将x+y看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2,再将A还原,原式=(x+y+1)2.
上述材料解题过程用到了整体思想,整体思想是数学中常用方法,请根据上面方法完成下列各小题.
(1)因式分解:(m+n)2﹣6(m+n)+9;
(2)设M=(a﹣b)(a﹣b﹣2)+1.
①因式分解M;
②若M=0,求a﹣b的值.
24. 如图.AD为△ABC的中线,BE为△ABD的中线,EF⊥BC于点F.
(1)在△BEF中,请指出边EF上的高;
(2)若BD=5,EF=2,求△ACD的面积;
(3)若AB=m,AC=n,若△ACD的周长为a,请用含m,n,a的式子表示△ABD的周长.
25. 如图,已知在△ABC中,AE平分△ABC的外角∠PAC,DE垂直平分BC,分别交BC,AC,AE于点D,F,E,分别过点E作EQAP,EHAC,垂足分别为Q,H.
(1)求证:BQ=CH;
(2)若AQ=4,BQ=12,求AC的长.
26. 如图,已知在等边三角形ABC中,AB=AC=BC=20厘米,CD=8厘米,点M以6厘米/秒的速度运动,点M从点C出发,同时点N从点B出发,设运动时间为t秒.
(1)若点M在线段CB上运动,点N在线段BA上运动,点N的运动速度与点M的运动速度相等.
①当t=2时,△BMN和△CDM是否全等?请说明理由;
②当点M,N的运动时间t为______秒时,△BMN是一个直角三角形;
(2)若点M在线段CB上运动,点N在线段BA上运动,但点N的运动速度与点M的运动速度不相等,它们同时出发,是否存在t值,使得△BMN和△CDM全等?若存在,求出t的值及点N的运动速度;若不存在,请说明理由;
(3)已知点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,两点都按顺时针方向沿△ABC三边运动,经过50秒,点M与点N第一次相遇,则点N的运动速度是______厘米/秒.
2021~2022学年八年级第一学期期末考试
数学(人教版)
一、选择题.(本题共有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题所给四个选项中,只有一项符合题目要求)
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】D
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】A
【9题答案】
【答案】A
【10题答案】
【答案】B
【11题答案】
【答案】B
【12题答案】
【答案】D
【13题答案】
【答案】B
【14题答案】
【答案】D
【15题答案】
【答案】C
【16题答案】
【答案】D
二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
【17题答案】
【答案】 ①. 27 ②. -4
【18题答案】
【答案】 ①. ②. 400
【19题答案】
【答案】 ①. 4 ②. 5
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
【20题答案】
【答案】(1)
(2)m
【21题答案】
【答案】(1)图见解析;4;-4;-3
(2)(0,3)
【22题答案】
【答案】(1)
(2)0
【23题答案】
【答案】(1)
(2)①;②1
【24题答案】
【答案】(1)边EF上的高是BF;
(2)S△ACD=10;
(3)△ABD的周长为m+a-n.
【25题答案】
【答案】(1)见解析 (2)16
【26题答案】
【答案】(1)① 全等,理由见解析;② 或
(2)存在,,厘米|秒
(3)5.6或6.8
数学(人教版)
一、选择题.(本题共有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题所给四个选项中,只有一项符合题目要求)
1. 将一张长方形纸对折,然后用笔尖在纸上扎出“B”,再把纸铺平,可以看到的是( )
A. B. C. D.
2. 某公司运用5G技术,下载一个2.4M的文件大约只需要0.000048秒,则0.000048用科学记数法表示为( )
A. B. C. D.
3. 下列选项是最简分式的是( )
A. B. C. D.
4. 将多项式利用提公因式法分解因式,则提取的公因式为( )
A. B. ab C. a D. b
5. 在平面直角坐标系中,点A(m+1,5)与点B(3,n)关于y轴对称,则m,n的值分别为( )
A. m=-4,n=5 B. m=-4,n=3 C. m=2,n=5 D. m=-2,n=5
6. 如图,将一张含有角三角形纸片的两个顶点叠放在长方形纸条的两条对边上,若,则的度数为( )
A. B. C. D.
7. 如图,已知Rt△ABD≌Rt△CDB,则∠ADB+∠C=( )
A. 70° B. 80° C. 90° D. 无法确定
8. 已知,,则a与b的大小关系为( )
A. a>b B. a9. 小明用尺规在△ABC上作图,并留下如图所示的痕迹,若AB=6,AC=4,则△ABD与△ACD的面积之比为( )
A. B. C. D.
10. 如图是一款圣诞帽,该帽子的下方是正六边形ABCDEF,延长BA,EF,交于点G,则帽子的顶部△GAF的形状是( )
A. 只有两边相等的等腰三角形 B. 等边三角形
C. 直角三角形 D. 无法确定
11. 如图,A,B,C,D是四个村庄,B,D,C在一条东西走向公路的沿线上,BD=1km,DC=1km,村庄A和C,A和D间也有公路相连,且公路AD是南北走向,AC=3km,只有A和B之间由于间隔了一个小湖,无直接相连的公路.现决定在湖面上造一座桥,测得AE=1.2km,BF=0.7km,则建造的桥长至少为( )
A. 1.2km B. 1.1km C. 1km D. 0.7km
12. 若(x-a)(x-5)=x2-bx+10,则a+b的值为( )
A 2 B. 5 C. 7 D. 9
13. 如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若AD=3,△ACE的周长为13,则△ABC的周长为( )
A. 18 B. 19 C. 26 D. 29
14. 若关于x的分式方程有正整数解,则整数m的值是( )
A. 3 B. 5 C. 3或5 D. 3或4
15. 如图,已知AD是△ABC的中线,E,F分别是AD和AD延长线上的点,且DE=DF,连接BF,CE.下列说法正确的是( )
①BD=CD;②∠BAD=∠CAD;③△BDF≌△CDE;④BF∥CE;⑤CE=AE
A. ①② B. ③⑤ C. ①③④ D. ①④⑤
16. 已知在平面直角坐标系xOy中,点,,,其中m>a,a<1,n>0,若△ABC是等腰直角三角形,且AB=BC,则m的取值范围是( )
A. m<3 B. m>3 C. 0
17. 已知 x+y-3=0,,则______,x-y的值为______.
18. 现有6000米钢轨需要铺设,为确保通车时间,实际施工时每天铺设的长度是原计划的2倍,结果提前15天完成任务.设原计划每天铺设钢轨x米.
(1)根据题意,可列分式方程为______;
(2)实际施工时每天铺设钢轨的长度为______米.
19. 如图,已知在△ABC中,AD平分∠BAC,BDAD于点D,过点D作,交AB于点E.
(1)若AE=4,则DE的长为______;
(2)若AB=10,则DE的长为______.
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
20. 按要求完成下列各小题.
(1)计算:;
(2)计算:.
21. 如图,在平面直角坐标系中,已知△ABC与关于x轴对称,它们的三个顶点坐标如下表所示.
△ABC
(1)在图中画出,并填空:a=______;b=______;d=______;
(2)P是y轴上一个动点,当PA+PB的值最小时,点P的坐标为______.
22. 已知分式方程有解,其中“■”表示一个数.
(1)若“■”表示的数为7,求分式方程的解;
(2)嘉淇回忆说:由于抄题时等号右边的数值抄错,导致找不到原题目,但可以肯定的是“■”是-1或0,试确定“■”表示的数.
23 阅读材料:将(x+y)2+2(x+y)+1分解因式.
解:将x+y看成整体,令x+y=A,则原式=A2+2A+1=(A+1)2,再将A还原,原式=(x+y+1)2.
上述材料解题过程用到了整体思想,整体思想是数学中常用方法,请根据上面方法完成下列各小题.
(1)因式分解:(m+n)2﹣6(m+n)+9;
(2)设M=(a﹣b)(a﹣b﹣2)+1.
①因式分解M;
②若M=0,求a﹣b的值.
24. 如图.AD为△ABC的中线,BE为△ABD的中线,EF⊥BC于点F.
(1)在△BEF中,请指出边EF上的高;
(2)若BD=5,EF=2,求△ACD的面积;
(3)若AB=m,AC=n,若△ACD的周长为a,请用含m,n,a的式子表示△ABD的周长.
25. 如图,已知在△ABC中,AE平分△ABC的外角∠PAC,DE垂直平分BC,分别交BC,AC,AE于点D,F,E,分别过点E作EQAP,EHAC,垂足分别为Q,H.
(1)求证:BQ=CH;
(2)若AQ=4,BQ=12,求AC的长.
26. 如图,已知在等边三角形ABC中,AB=AC=BC=20厘米,CD=8厘米,点M以6厘米/秒的速度运动,点M从点C出发,同时点N从点B出发,设运动时间为t秒.
(1)若点M在线段CB上运动,点N在线段BA上运动,点N的运动速度与点M的运动速度相等.
①当t=2时,△BMN和△CDM是否全等?请说明理由;
②当点M,N的运动时间t为______秒时,△BMN是一个直角三角形;
(2)若点M在线段CB上运动,点N在线段BA上运动,但点N的运动速度与点M的运动速度不相等,它们同时出发,是否存在t值,使得△BMN和△CDM全等?若存在,求出t的值及点N的运动速度;若不存在,请说明理由;
(3)已知点N的运动速度与点M的运动速度不相等,点N从点B出发,点M以原来的运动速度从点C同时出发,两点都按顺时针方向沿△ABC三边运动,经过50秒,点M与点N第一次相遇,则点N的运动速度是______厘米/秒.
2021~2022学年八年级第一学期期末考试
数学(人教版)
一、选择题.(本题共有16个小题,共42分.1~10小题各3分;11~16小题各2分.在每小题所给四个选项中,只有一项符合题目要求)
【1题答案】
【答案】C
【2题答案】
【答案】C
【3题答案】
【答案】D
【4题答案】
【答案】D
【5题答案】
【答案】A
【6题答案】
【答案】D
【7题答案】
【答案】C
【8题答案】
【答案】A
【9题答案】
【答案】A
【10题答案】
【答案】B
【11题答案】
【答案】B
【12题答案】
【答案】D
【13题答案】
【答案】B
【14题答案】
【答案】D
【15题答案】
【答案】C
【16题答案】
【答案】D
二、填空题.(本大题有3个小题,每小题有2个空,每空2分,共12分.把答案写在题中横线上)
【17题答案】
【答案】 ①. 27 ②. -4
【18题答案】
【答案】 ①. ②. 400
【19题答案】
【答案】 ①. 4 ②. 5
三、解答题.(本大题共7个小题,共66分.解答应写出文字说明、证明过程或演算步骤)
【20题答案】
【答案】(1)
(2)m
【21题答案】
【答案】(1)图见解析;4;-4;-3
(2)(0,3)
【22题答案】
【答案】(1)
(2)0
【23题答案】
【答案】(1)
(2)①;②1
【24题答案】
【答案】(1)边EF上的高是BF;
(2)S△ACD=10;
(3)△ABD的周长为m+a-n.
【25题答案】
【答案】(1)见解析 (2)16
【26题答案】
【答案】(1)① 全等,理由见解析;② 或
(2)存在,,厘米|秒
(3)5.6或6.8
同课章节目录
