沪科版八年级数学上册 12.2一次函数(第2课时) 教案(表格式)
文档属性
| 名称 | 沪科版八年级数学上册 12.2一次函数(第2课时) 教案(表格式) |

|
|
| 格式 | docx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览



文档简介
第12章 一次函数
12.2 一次函数
第2课时 一次函数的图象及其性质
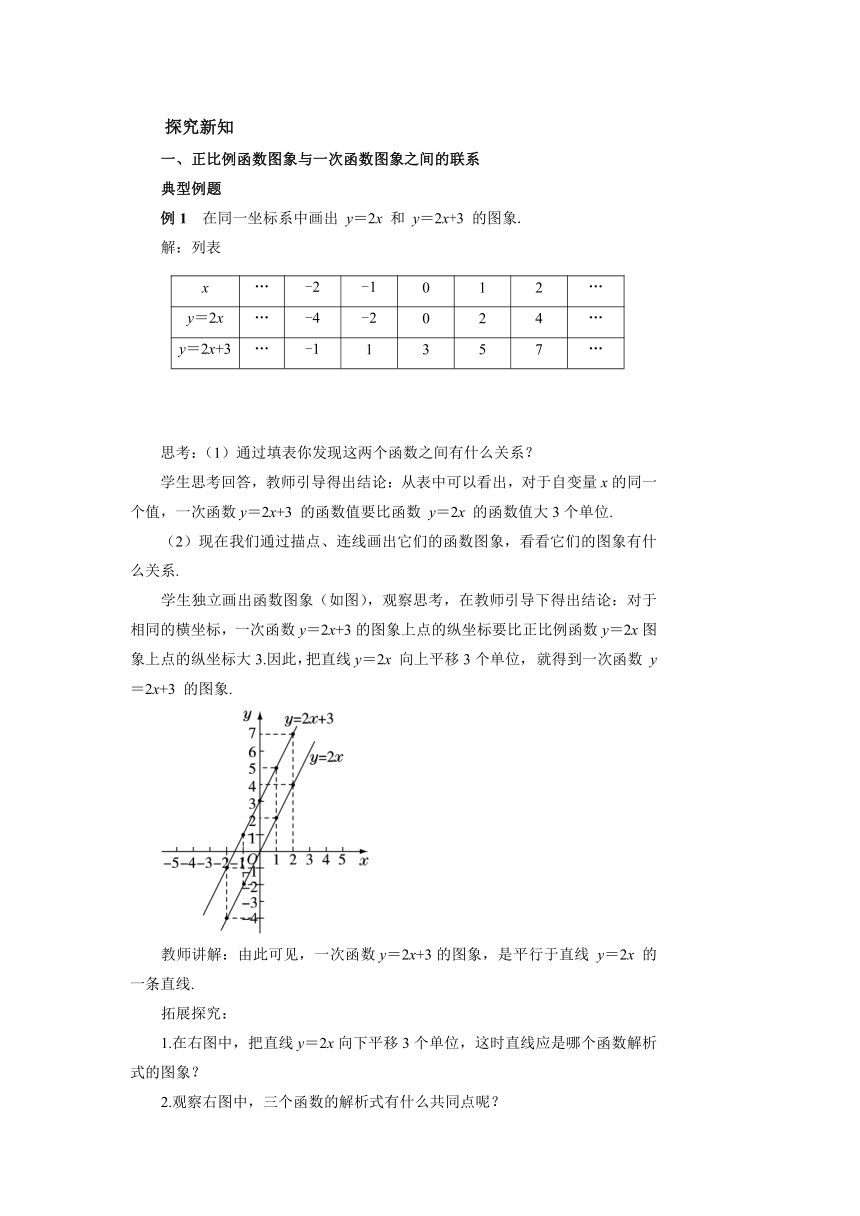
教学目标 1.会用两点法画一次函数图象. 2.利用数形结合的思想,分析一次函数与正比例函数的联系及一次函数的性质. 教学重难点 重点:分析一次函数与正比例函数解析式和图象之间的联系 难点:画一次函数图象,掌握一次函数的图象及其性质 教学过程 知识回顾 提问:1.什么是一次函数? 一般地,形如 y=kx+b ( k,b为常数,且 k≠0)的函数叫做一次函数. 2.什么是正比例函数? 形如 y=kx (k为常数,且k≠0) 的函数 ,叫做正比例函数. 3.正比例函数与一次函数有什么关系? 正比例函数是一次函数一般式b=0时的特殊情形 .即 :正比例函数一定是一次函数,而一次函数不一定是正比例函数. 4.正比例函数 y=kx ( k为常数,且k≠0 ) 的图象有什么性质? 对于正比例函数y=kx,当k>0 时,y=kx 的图象在一、三象限,且y随x的增大而增大;当k<0时,y=kx的图象在二、四象限,且y随x的增大而减小. 新课导入 正比例函数y=kx (k为常数,且k≠0) 的函数图象是一条经过原点的直线 ,对于一次函数 y=kx+b (k,b为常数,且k≠0),当b≠0时,它的图象又是什么呢? 下面,我们一起来研究一次函数的图象及其性质. 探究新知 一、正比例函数图象与一次函数图象之间的联系 典型例题 例1 在同一坐标系中画出 y=2x 和 y=2x+3 的图象. 解:列表 x…-2-1012…y=2x…-4-2024…y=2x+3…-11357…
思考:(1)通过填表你发现这两个函数之间有什么关系? 学生思考回答,教师引导得出结论:从表中可以看出,对于自变量x的同一个值,一次函数y=2x+3 的函数值要比函数 y=2x 的函数值大3个单位. (2)现在我们通过描点、连线画出它们的函数图象,看看它们的图象有什么关系. 学生独立画出函数图象(如图),观察思考,在教师引导下得出结论:对于相同的横坐标,一次函数y=2x+3的图象上点的纵坐标要比正比例函数y=2x图象上点的纵坐标大3.因此,把直线y=2x 向上平移3个单位, 就得到一次函数 y=2x+3 的图象. 教师讲解:由此可见,一次函数y=2x+3的图象,是平行于直线 y=2x 的一条直线. 拓展探究: 1.在右图中,把直线y=2x向下平移3个单位,这时直线应是哪个函数解析式的图象? 2.观察右图中,三个函数的解析式有什么共同点呢? 3.观察右图中,三个函数的图象,你发现了什么? 4.观察三个函数的图象和解析式,你能得到什么结论? 学生独立完成,小组交流讨论,并展示成果. 1.y=2x-3; 2.三个函数解析式 k值相等,b值不同; 3.三个函数图象都是直线,且互相平行; 4.当两个一次函数的k值相等,b值不同时,这两个一次函数的图象是互相平行的. 教师讲解: 一般地,一次函数 y=kx+b (k,b为常数,且k≠0) 的图象是平行于直线 y=kx 的一条直线,因此,我们以后把一次函数 y=kx+b (k,b为常数,且k≠0) 的图象叫做直线y=kx+b. 拓展:(1)所有一次函数y=kx+b的图象都是直线. (2)直线y=kx+b与直线y=kx相互平行. (3)直线y=kx+b可以看作由直线y=kx平移得到: 当b>0时,向上平移b个单位长度; 当b<0时,向下平移b个单位长度. 典型例题 例2 已知直线 y=kx+b (k≠0) 平行于直线 y=-2x+1,且过点(-2,4),分别求出k和b. 解:因为直线y=kx+b (k≠0) 与直线 y=-2x+1平行,所以k=-2. 又因为直线y=kx+b (k≠0) 经过点(-2,4),所以 4=-2×(-2)+b, 解得b=0.综上所述,k=-2,b=0. 两点法画一次函数图象 探究:完成下列填空,思考怎样快速作出一个一次函数的图象? 直线 y=2x+3与y轴的交点坐标是 ,与x轴的交点坐标是 . 直线 y=2x-3与y轴的交点坐标是 ,与x轴的交点坐标是 . (3)y=kx+b 与y轴的交点坐标是 ,与x轴的交点坐标是 . 教师讲解: 画一次函数 y=kx+b (k≠0)的图象,若b≠0,通常取该直线与y轴的交点(0,b)和与x轴的交点,由两点确定一条直线得一次函数的图象. 直线 y=kx+b 与y轴相交于点(0,b),b叫做直线y=kx+b在y轴上的截距,简称截距. 注意:截距不同于距离,截距可正可负,也可以为零.截距不同,图象与y轴的交点就不同. 典型例题 例3 画出直线 y=x-2,并求它的截距. x03y-20
解:列表: 过点(0,-2)和点(3,0)画一线, 就得直线y=x-2. 它的截距是-2. 三、一次函数的性质 探究1:在同一平面直角坐标系中,画下列函数的图象: y=3x+1,y=2x-3,y=x+4. 学生独立完成,画出函数图象. 观察函数图象,分析这三个函数解析式有什么共同的特点? 结合正比例函数的性质,想一想一次函数的图象有什么特征? 学生独立完成,并展示探究成果,教师引导纠正,得出正确答案. (1) 这三个解析式k>0,b不相同. 当k>0时,y=kx+b 的图象经过的象限中必有一、三象限, 且 y随 x的 增大而增大(图象是自左向右上升的). 探究2:观察右图中的三个函数的解析式和图象,你能得到什么结论? 学生独立思考,回答问题,教师引导得出正确结论: 当k<0时,y=kx+b 的图象经过的象限中必有二、四象限,且y随x的增大而减小(图象是自左向右下降的). 思考:一次函数解析式y=kx+b(k,b是常数,k≠0)中, k,b的正负对函数图象及性质有什么影响? 观察下列图象分析k、b的取值. 学生独立思考,小组讨论,回答问题. 教师讲解: (1)当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大. b>0时,直线经过第一、二、三象限; b<0时,直线经过第一、三、四象限. (2)当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小. ① b>0时,直线经过第 一、二、四象限; ② b<0时,直线经过第二、三、四象限. 典型例题 例4 已知一次函数 y=(1-2m)x+m-1,求满足下列条件的m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限. 解:(1)由题意得1-2m>0,解得m<. (2)由题意得1-2m≠0且m-1<0,即m<1且m≠. (3)由题意得1-2m<0且m-1<0,解得<m<1. 课堂练习 1.在平面直角坐标系中,函数y=-2x+3的图象经过( ) A.一、二、三象限 B.二、三、四象限 C.一、三、四象限 D.一、二、四象限 2.一次函数 y=x-2 的大致图象为( ) A B C D 3.一次函数y=(m2+1)x+a+1(m,a为常数)的图象不可能经过的象限为( ) A.一、二、三 B.一、三 C.一、二、四 D.一、三、四 4.若一次函数y=kx+1(k为常数,k≠0)的图象经过第一、二、三象限,则k的取值范围是_______ . 5.直线y=2x-3 与x 轴交点的坐标为_______;与y轴交点的坐标为______;图象经过第 象限, y 随x 的增大而________. 6.若直线y=kx+2与y=3x-1平行,则k= . 7.点A(-1,y),B(3,y)是直线y=kx+b(k<0)上的两点,则y-y 0(填“>”或“<”). 参考答案 1.D 2.C 3.C 4.k>0 5.(1.5,0) (0,-3) 一、三、四 增大 6.k=3 7.> 课堂小结 图象k,b的符号k>0, b>0k>0, b<0k<0, b>0k<0, b<0经过象限一、二、三一、三、四一、二、四二、三、四增减性y随x的增 大而增大y随x的增 大而增大y随x的增 大而减小y随x的增 大而减小
布置作业 教材38页练习1,2,3题; 教材39页练习1,2,3,4,5题. 板书设计 第2课时 一次函数的图象及其性质 当k>0,b>0时,直线经过第一、二、三象限; 当k>0,b<0时,直线经过第一、三、四象限; 当k<0,b>0时,直线经过第一、二、四象限; 当k<0,b<0时,直线经过第二、三、四象限. 例 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限. 解:(1)由题意得1-2m>0,解得m<. (2)由题意得1-2m≠0且m-1<0,即m<1且m≠ (3)由题意得1-2m<0且m-1<0,解得<m<1.
12.2 一次函数
第2课时 一次函数的图象及其性质
教学目标 1.会用两点法画一次函数图象. 2.利用数形结合的思想,分析一次函数与正比例函数的联系及一次函数的性质. 教学重难点 重点:分析一次函数与正比例函数解析式和图象之间的联系 难点:画一次函数图象,掌握一次函数的图象及其性质 教学过程 知识回顾 提问:1.什么是一次函数? 一般地,形如 y=kx+b ( k,b为常数,且 k≠0)的函数叫做一次函数. 2.什么是正比例函数? 形如 y=kx (k为常数,且k≠0) 的函数 ,叫做正比例函数. 3.正比例函数与一次函数有什么关系? 正比例函数是一次函数一般式b=0时的特殊情形 .即 :正比例函数一定是一次函数,而一次函数不一定是正比例函数. 4.正比例函数 y=kx ( k为常数,且k≠0 ) 的图象有什么性质? 对于正比例函数y=kx,当k>0 时,y=kx 的图象在一、三象限,且y随x的增大而增大;当k<0时,y=kx的图象在二、四象限,且y随x的增大而减小. 新课导入 正比例函数y=kx (k为常数,且k≠0) 的函数图象是一条经过原点的直线 ,对于一次函数 y=kx+b (k,b为常数,且k≠0),当b≠0时,它的图象又是什么呢? 下面,我们一起来研究一次函数的图象及其性质. 探究新知 一、正比例函数图象与一次函数图象之间的联系 典型例题 例1 在同一坐标系中画出 y=2x 和 y=2x+3 的图象. 解:列表 x…-2-1012…y=2x…-4-2024…y=2x+3…-11357…
思考:(1)通过填表你发现这两个函数之间有什么关系? 学生思考回答,教师引导得出结论:从表中可以看出,对于自变量x的同一个值,一次函数y=2x+3 的函数值要比函数 y=2x 的函数值大3个单位. (2)现在我们通过描点、连线画出它们的函数图象,看看它们的图象有什么关系. 学生独立画出函数图象(如图),观察思考,在教师引导下得出结论:对于相同的横坐标,一次函数y=2x+3的图象上点的纵坐标要比正比例函数y=2x图象上点的纵坐标大3.因此,把直线y=2x 向上平移3个单位, 就得到一次函数 y=2x+3 的图象. 教师讲解:由此可见,一次函数y=2x+3的图象,是平行于直线 y=2x 的一条直线. 拓展探究: 1.在右图中,把直线y=2x向下平移3个单位,这时直线应是哪个函数解析式的图象? 2.观察右图中,三个函数的解析式有什么共同点呢? 3.观察右图中,三个函数的图象,你发现了什么? 4.观察三个函数的图象和解析式,你能得到什么结论? 学生独立完成,小组交流讨论,并展示成果. 1.y=2x-3; 2.三个函数解析式 k值相等,b值不同; 3.三个函数图象都是直线,且互相平行; 4.当两个一次函数的k值相等,b值不同时,这两个一次函数的图象是互相平行的. 教师讲解: 一般地,一次函数 y=kx+b (k,b为常数,且k≠0) 的图象是平行于直线 y=kx 的一条直线,因此,我们以后把一次函数 y=kx+b (k,b为常数,且k≠0) 的图象叫做直线y=kx+b. 拓展:(1)所有一次函数y=kx+b的图象都是直线. (2)直线y=kx+b与直线y=kx相互平行. (3)直线y=kx+b可以看作由直线y=kx平移得到: 当b>0时,向上平移b个单位长度; 当b<0时,向下平移b个单位长度. 典型例题 例2 已知直线 y=kx+b (k≠0) 平行于直线 y=-2x+1,且过点(-2,4),分别求出k和b. 解:因为直线y=kx+b (k≠0) 与直线 y=-2x+1平行,所以k=-2. 又因为直线y=kx+b (k≠0) 经过点(-2,4),所以 4=-2×(-2)+b, 解得b=0.综上所述,k=-2,b=0. 两点法画一次函数图象 探究:完成下列填空,思考怎样快速作出一个一次函数的图象? 直线 y=2x+3与y轴的交点坐标是 ,与x轴的交点坐标是 . 直线 y=2x-3与y轴的交点坐标是 ,与x轴的交点坐标是 . (3)y=kx+b 与y轴的交点坐标是 ,与x轴的交点坐标是 . 教师讲解: 画一次函数 y=kx+b (k≠0)的图象,若b≠0,通常取该直线与y轴的交点(0,b)和与x轴的交点,由两点确定一条直线得一次函数的图象. 直线 y=kx+b 与y轴相交于点(0,b),b叫做直线y=kx+b在y轴上的截距,简称截距. 注意:截距不同于距离,截距可正可负,也可以为零.截距不同,图象与y轴的交点就不同. 典型例题 例3 画出直线 y=x-2,并求它的截距. x03y-20
解:列表: 过点(0,-2)和点(3,0)画一线, 就得直线y=x-2. 它的截距是-2. 三、一次函数的性质 探究1:在同一平面直角坐标系中,画下列函数的图象: y=3x+1,y=2x-3,y=x+4. 学生独立完成,画出函数图象. 观察函数图象,分析这三个函数解析式有什么共同的特点? 结合正比例函数的性质,想一想一次函数的图象有什么特征? 学生独立完成,并展示探究成果,教师引导纠正,得出正确答案. (1) 这三个解析式k>0,b不相同. 当k>0时,y=kx+b 的图象经过的象限中必有一、三象限, 且 y随 x的 增大而增大(图象是自左向右上升的). 探究2:观察右图中的三个函数的解析式和图象,你能得到什么结论? 学生独立思考,回答问题,教师引导得出正确结论: 当k<0时,y=kx+b 的图象经过的象限中必有二、四象限,且y随x的增大而减小(图象是自左向右下降的). 思考:一次函数解析式y=kx+b(k,b是常数,k≠0)中, k,b的正负对函数图象及性质有什么影响? 观察下列图象分析k、b的取值. 学生独立思考,小组讨论,回答问题. 教师讲解: (1)当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大. b>0时,直线经过第一、二、三象限; b<0时,直线经过第一、三、四象限. (2)当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小. ① b>0时,直线经过第 一、二、四象限; ② b<0时,直线经过第二、三、四象限. 典型例题 例4 已知一次函数 y=(1-2m)x+m-1,求满足下列条件的m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限. 解:(1)由题意得1-2m>0,解得m<. (2)由题意得1-2m≠0且m-1<0,即m<1且m≠. (3)由题意得1-2m<0且m-1<0,解得<m<1. 课堂练习 1.在平面直角坐标系中,函数y=-2x+3的图象经过( ) A.一、二、三象限 B.二、三、四象限 C.一、三、四象限 D.一、二、四象限 2.一次函数 y=x-2 的大致图象为( ) A B C D 3.一次函数y=(m2+1)x+a+1(m,a为常数)的图象不可能经过的象限为( ) A.一、二、三 B.一、三 C.一、二、四 D.一、三、四 4.若一次函数y=kx+1(k为常数,k≠0)的图象经过第一、二、三象限,则k的取值范围是_______ . 5.直线y=2x-3 与x 轴交点的坐标为_______;与y轴交点的坐标为______;图象经过第 象限, y 随x 的增大而________. 6.若直线y=kx+2与y=3x-1平行,则k= . 7.点A(-1,y),B(3,y)是直线y=kx+b(k<0)上的两点,则y-y 0(填“>”或“<”). 参考答案 1.D 2.C 3.C 4.k>0 5.(1.5,0) (0,-3) 一、三、四 增大 6.k=3 7.> 课堂小结 图象k,b的符号k>0, b>0k>0, b<0k<0, b>0k<0, b<0经过象限一、二、三一、三、四一、二、四二、三、四增减性y随x的增 大而增大y随x的增 大而增大y随x的增 大而减小y随x的增 大而减小
布置作业 教材38页练习1,2,3题; 教材39页练习1,2,3,4,5题. 板书设计 第2课时 一次函数的图象及其性质 当k>0,b>0时,直线经过第一、二、三象限; 当k>0,b<0时,直线经过第一、三、四象限; 当k<0,b>0时,直线经过第一、二、四象限; 当k<0,b<0时,直线经过第二、三、四象限. 例 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值: (1)函数值y 随x的增大而增大; (2)函数图象与y 轴的负半轴相交; (3)函数的图象过第二、三、四象限. 解:(1)由题意得1-2m>0,解得m<. (2)由题意得1-2m≠0且m-1<0,即m<1且m≠ (3)由题意得1-2m<0且m-1<0,解得<m<1.
