三角函数模型的简单应用[上学期]
文档属性
| 名称 | 三角函数模型的简单应用[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 96.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-03-27 00:00:00 | ||
图片预览



文档简介
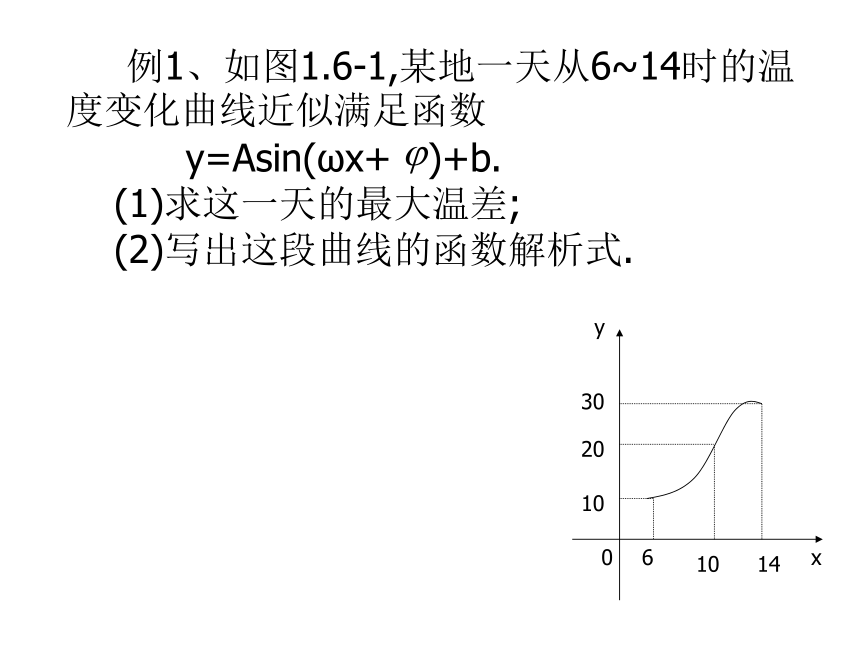
课件11张PPT。1.6 三角函数模型的简单应用 例1、如图1.6-1,某地一天从6~14时的温度变化曲线近似满足函数
y=Asin(ωx+ )+b.
(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.解:(1)由图可知,这段时间的最大温差是200C.(2)从图中可以看出,从6~14时的图象是函数y=
Asin(vωx+ )+b的半个周期的图象,所以 A= (30-10)=10,
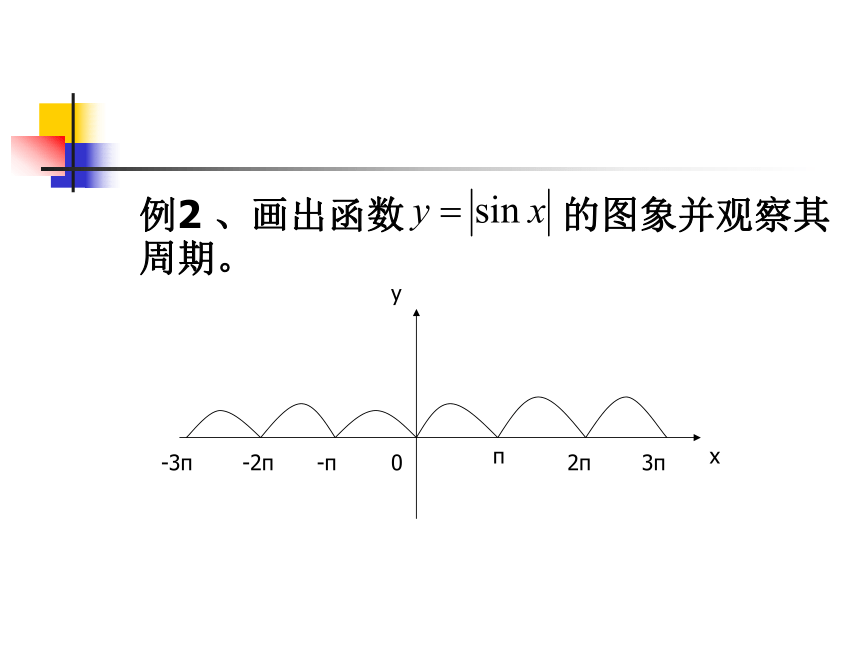
b= (30+10)=20,∵ 将x=6,y=10代入上式,解的综上,所求解析式为例2 、画出函数 的图象并观察其
周期。解:函数图象如图所示。从图中可以看出,函数 是以π为
周期的波浪形曲线。
我们也可以这样进行验证:由于所以,函数 是以π为周期的函数。例3、如图,设地球表面某地正午太阳高度
角为θ,δ为此时太阳直射纬度, 为该地
的纬度值,那么这三个量之间的关系是
当地夏半年δ取正值,
冬半年δ取负值。
如果在北京地区(纬度数约为北纬400)
的一幢高为h0的楼房北面盖一新楼,要使新
楼一层正午的太阳全年不被前面的楼房遮挡,
两楼的距离不应小于多少?
ABMC40°0°23°26′-23°26′图示解:如图,A、B、C分别为太阳直射北回归
线、赤道、南回归线时楼顶在地面上的投影
点。要使新楼一层正午的太阳全年不被前面
的楼房遮挡,应取太阳直射南回归线的情况
考虑,此时的太阳直射纬度为-23026’.依题意
两楼的间距应不小于MC.
根据太阳高度角的定义,有即在盖楼时,为使后楼不被前楼遮挡,要
留出相当于楼高两倍的间距。课本第69页例4动画演示图示 五、总结提炼
(1) 三角应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图.
②建模:根据已知条件与求解目标,把已知量与求
解量尽量集中在有关的三角形中,建立一个解三角形的
数学模型.
③求解:利用三角形,求得数学模型的解.
④检验:检验上述所求的解是否符合实际意义,从
而得出实际问题的解.即解三角应用题的基本思路
y=Asin(ωx+ )+b.
(1)求这一天的最大温差;
(2)写出这段曲线的函数解析式.解:(1)由图可知,这段时间的最大温差是200C.(2)从图中可以看出,从6~14时的图象是函数y=
Asin(vωx+ )+b的半个周期的图象,所以 A= (30-10)=10,
b= (30+10)=20,∵ 将x=6,y=10代入上式,解的综上,所求解析式为例2 、画出函数 的图象并观察其
周期。解:函数图象如图所示。从图中可以看出,函数 是以π为
周期的波浪形曲线。
我们也可以这样进行验证:由于所以,函数 是以π为周期的函数。例3、如图,设地球表面某地正午太阳高度
角为θ,δ为此时太阳直射纬度, 为该地
的纬度值,那么这三个量之间的关系是
当地夏半年δ取正值,
冬半年δ取负值。
如果在北京地区(纬度数约为北纬400)
的一幢高为h0的楼房北面盖一新楼,要使新
楼一层正午的太阳全年不被前面的楼房遮挡,
两楼的距离不应小于多少?
ABMC40°0°23°26′-23°26′图示解:如图,A、B、C分别为太阳直射北回归
线、赤道、南回归线时楼顶在地面上的投影
点。要使新楼一层正午的太阳全年不被前面
的楼房遮挡,应取太阳直射南回归线的情况
考虑,此时的太阳直射纬度为-23026’.依题意
两楼的间距应不小于MC.
根据太阳高度角的定义,有即在盖楼时,为使后楼不被前楼遮挡,要
留出相当于楼高两倍的间距。课本第69页例4动画演示图示 五、总结提炼
(1) 三角应用题的一般步骤是:
①分析:理解题意,分清已知与未知,画出示意图.
②建模:根据已知条件与求解目标,把已知量与求
解量尽量集中在有关的三角形中,建立一个解三角形的
数学模型.
③求解:利用三角形,求得数学模型的解.
④检验:检验上述所求的解是否符合实际意义,从
而得出实际问题的解.即解三角应用题的基本思路
