平面向量的数量积[上学期]
图片预览




文档简介
课件10张PPT。教学目的:
1.掌握平面向量的数量积及其几何意义;
2.掌握平面向量数量积的重要性质及运算律;
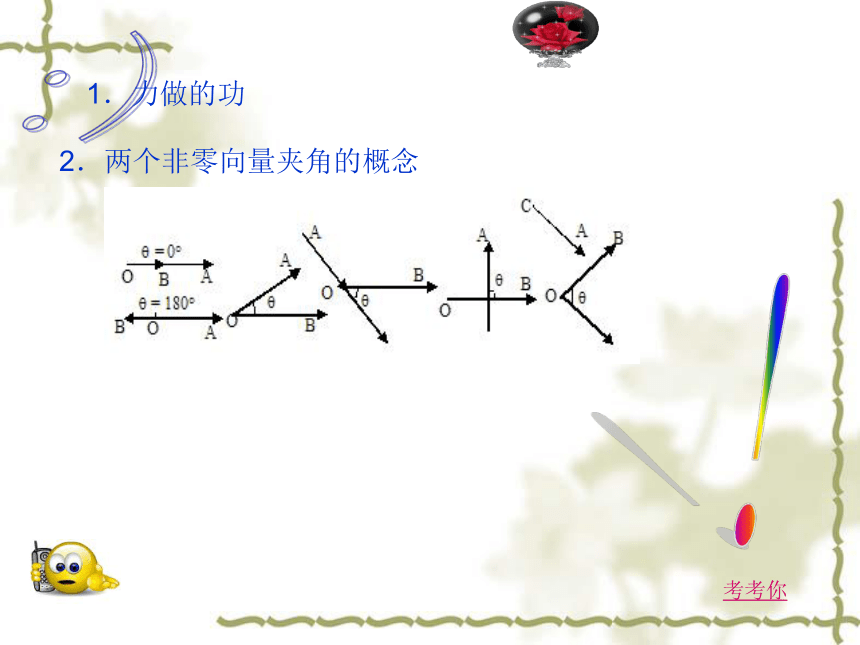
3.了解用平面向量的数量积可以处理有关长度、角度和垂直的问题; 4.掌握向量垂直的条件.第7课时§2.4平面向量的数量积一、 平面向量的数量积的物理背景及其含义$﹫·一、复习引入:1. 向量共线定理 2.平面向量基本定理 3.平面向量的坐标表示4.平面向量的坐标运算5.∥ (?)的条件 6.两个非零向量夹角的概念?:(过程下一张小车运动考考你!:)1.力做的功 2.两个非零向量夹角的概念返回2.平面向量数量积(内积)的定义:已知两个非零向量a与b,
它们的夹角是θ,则数量|a||b|cos?叫a与b的数量积,
记作a?b,即有a?b = |a||b|cos?,
(0≤θ≤π).并规定0与任何向量的数量积为0.?探究:1.两个向量的数量积与同实数积有什么区别?2.两个向量的数量积与实数同向量的积有什么区别?返回(1)两个向量的数量积是一个实数,不是向量,符号由cos?的符号所决定.
(2)两个向量的数量积称为内积,写成a?b;今后要学到两个向量的外积a×b,
而a?b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,
既不能省略,也不能用“×”代替.
(3)在实数中,若a?0,且a?b=0,则b=0;但是在数量积中,若a?0,且a?b=0,
不能推出b=0.因为其中cos?有可能为0.
(4)已知实数a、b、c(b?0),则ab=bc ? a=c.但是a?b = b?c不能
得到 a=c
如右图:a?b = |a||b|cos? = |b||OA|,b?c = |b||c|cos? = |b||OA|
? a?b = b?c 但a ? c
(5)在实数中,有(a?b)c = a(b?c),但是(a?b)c ? a(b?c)
显然,这是因为左端是与c共线的向量,而右端是与a共线的向量,
而向量a与c不一定共线.两个向量的数量积与同实数积的区别两个向量的数量积与实数同向量的积的区别 两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量返回概念:作3.“投影”的图
定义:|b|cos?叫做向量b在a方向上的投影.
投影也是一个数量,不是向量;当?为锐角时投影为正值;
当?为钝角时投影为负值;当?为直角时投影为0;当? = 0?时投影
为 |b|;当? = 180?时投影为 ?|b|.
返回4.向量的数量积的几何意义:
数量积a?b等于a的长度与b在a方向上投影|b|cos?的乘积.
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量.1? e?a = a?e =|a|cos?
2? a?b ? a?b = 0
3? 当a与b同向时,a?b = |a||b|;当a与b反向时,a?b = ?|a||b|.
特别的a?a = |a|2或4? cos? =5? |a?b| ≤ |a||b|?练习:三、讲解范例:
例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.
例2 已知|a|=6, |b|=4, a与b的夹角为60o求(a+2b)·(a-3b).
例3 已知|a|=3, |b|=4, 且a与b不共线,k为何值时,
向量a+kb与a-kb互相垂直.
例4 判断正误,并简要说明理由.
①a·0=0;②0·a=0;③0-=④|a·b|=|a||b|;
⑤若a≠0,则对任一非零b有a·b≠0;
⑥a·b=0,则a与b中至少有一个为0;
⑦对任意向量a,b,с都有(a·b) ·c= a·(b ·c)
⑧a与b是两个单位向量,则a2=b2.谢谢
1.掌握平面向量的数量积及其几何意义;
2.掌握平面向量数量积的重要性质及运算律;
3.了解用平面向量的数量积可以处理有关长度、角度和垂直的问题; 4.掌握向量垂直的条件.第7课时§2.4平面向量的数量积一、 平面向量的数量积的物理背景及其含义$﹫·一、复习引入:1. 向量共线定理 2.平面向量基本定理 3.平面向量的坐标表示4.平面向量的坐标运算5.∥ (?)的条件 6.两个非零向量夹角的概念?:(过程下一张小车运动考考你!:)1.力做的功 2.两个非零向量夹角的概念返回2.平面向量数量积(内积)的定义:已知两个非零向量a与b,
它们的夹角是θ,则数量|a||b|cos?叫a与b的数量积,
记作a?b,即有a?b = |a||b|cos?,
(0≤θ≤π).并规定0与任何向量的数量积为0.?探究:1.两个向量的数量积与同实数积有什么区别?2.两个向量的数量积与实数同向量的积有什么区别?返回(1)两个向量的数量积是一个实数,不是向量,符号由cos?的符号所决定.
(2)两个向量的数量积称为内积,写成a?b;今后要学到两个向量的外积a×b,
而a?b是两个向量的数量的积,书写时要严格区分.符号“· ”在向量运算中不是乘号,
既不能省略,也不能用“×”代替.
(3)在实数中,若a?0,且a?b=0,则b=0;但是在数量积中,若a?0,且a?b=0,
不能推出b=0.因为其中cos?有可能为0.
(4)已知实数a、b、c(b?0),则ab=bc ? a=c.但是a?b = b?c不能
得到 a=c
如右图:a?b = |a||b|cos? = |b||OA|,b?c = |b||c|cos? = |b||OA|
? a?b = b?c 但a ? c
(5)在实数中,有(a?b)c = a(b?c),但是(a?b)c ? a(b?c)
显然,这是因为左端是与c共线的向量,而右端是与a共线的向量,
而向量a与c不一定共线.两个向量的数量积与同实数积的区别两个向量的数量积与实数同向量的积的区别 两个向量的数量积是一个实数,不是向量,符号
由cos?的符号所决定,而实数同向量的积是一个向量返回概念:作3.“投影”的图
定义:|b|cos?叫做向量b在a方向上的投影.
投影也是一个数量,不是向量;当?为锐角时投影为正值;
当?为钝角时投影为负值;当?为直角时投影为0;当? = 0?时投影
为 |b|;当? = 180?时投影为 ?|b|.
返回4.向量的数量积的几何意义:
数量积a?b等于a的长度与b在a方向上投影|b|cos?的乘积.
5.两个向量的数量积的性质:
设a、b为两个非零向量,e是与b同向的单位向量.1? e?a = a?e =|a|cos?
2? a?b ? a?b = 0
3? 当a与b同向时,a?b = |a||b|;当a与b反向时,a?b = ?|a||b|.
特别的a?a = |a|2或4? cos? =5? |a?b| ≤ |a||b|?练习:三、讲解范例:
例1 已知|a|=5, |b|=4, a与b的夹角θ=120o,求a·b.
例2 已知|a|=6, |b|=4, a与b的夹角为60o求(a+2b)·(a-3b).
例3 已知|a|=3, |b|=4, 且a与b不共线,k为何值时,
向量a+kb与a-kb互相垂直.
例4 判断正误,并简要说明理由.
①a·0=0;②0·a=0;③0-=④|a·b|=|a||b|;
⑤若a≠0,则对任一非零b有a·b≠0;
⑥a·b=0,则a与b中至少有一个为0;
⑦对任意向量a,b,с都有(a·b) ·c= a·(b ·c)
⑧a与b是两个单位向量,则a2=b2.谢谢
