正余弦定理综合运用[上学期]

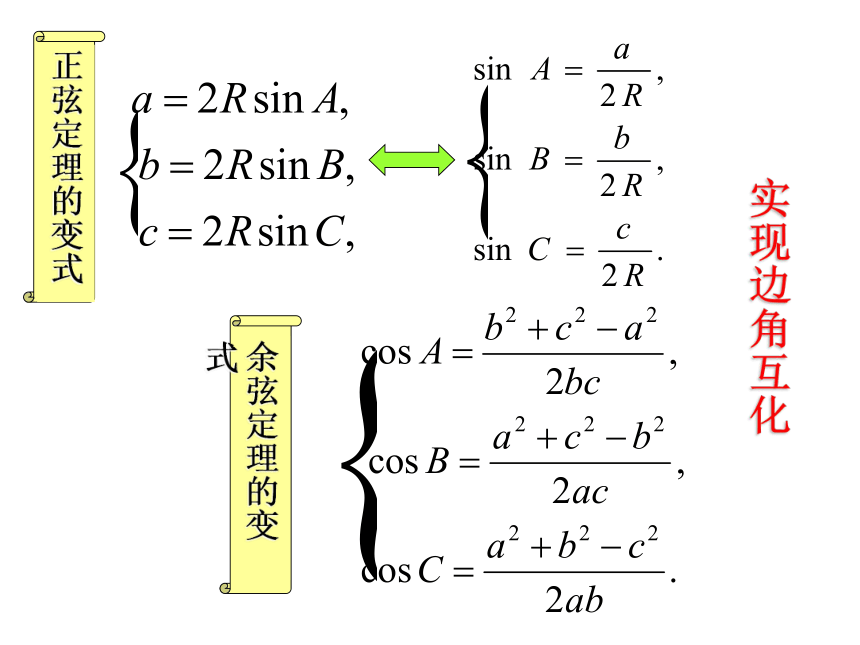
课件14张PPT。 课题:正弦定理、余弦定理综合运用汕头市聿怀中学数学组 阎锐2006-9-6余弦定理：正弦定理： 正弦定理、余弦定理综合运用复习：（R是三角形外接圆半径）实现边角互化例1：在△ABC中，已知acosA=bcosB，
试判断三角形的形状。解法一：（化角为边）由余弦定理得：是等腰三角形或直角三角形 题型一：判断三角形的形状解法二：（化边为角）由正弦定理得：是等腰三角形或直角三角形例1：在△ABC中，已知acosA=bcosB，
试判断三角形的形状。解题小结：
判断三角形形状时，一般考虑两种变形方向：一个是化角为边，再进行代数恒等变换求出三条边之间的关系式。另一个方向是化边为角，再进行三角恒等变换求出三个角之间的关系式。
两种转化主要应用正弦定理和余弦定理。在 中，若 ，则 是( )
A．等腰三角形 B．等腰直角三角形
C．直角三角形 D．等边三角形D 练习一题型二：三角形中的求值题例2：△ABC中，已知a=2，求bcosC＋ccosB的值。解:（化角为边）由余弦定理得：bcosC＋ccosB＝＋c·b·解法二:（化边为角） 由正弦定理得：bcosC＋ccosB
＝例2：△ABC中，已知a=2，求bcosC＋ccosB的值。射影定理：
a= bcosC＋ccosB,
b=ccosA+acosC,
c=acosB+bcosA解法一：代入 得： 由正弦定理得：（化边为角）例3：

解法二：由余弦定理得代入 得：整理得（化角为边）例3：解：由余弦定理知：（化边为角）练习二小结： 1、学会利用正弦、余弦定理解决两类题型：
（1） 判断三角形的形状；
（2） 三角形中的求值题。
2、两种题型思路的共同点就是从“统一”着眼， 或统一转化为三角函数，作三角变换；
或统一转化为边，作代数变换。3、解三角形中的求值题时还要注意综合运用
三角形的有关性质和三角公式进行变形。4、本节课渗透的主要数学思想：
转换的思想和方程的思想作业：2、试判断三角形的形状。求∠C的大小。