21.3 一元二次方程的实际应用 课件(共19张PPT)
文档属性
| 名称 | 21.3 一元二次方程的实际应用 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-22 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
一元二次方程的应用
人教版九年级上册
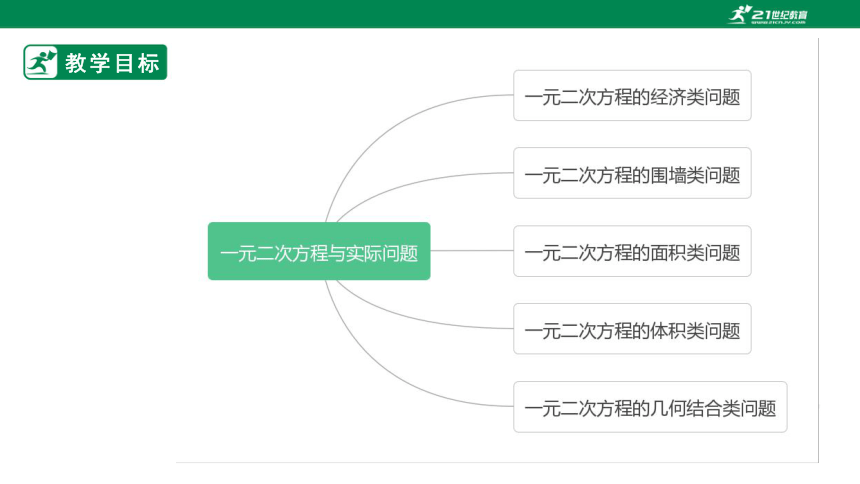
教学目标
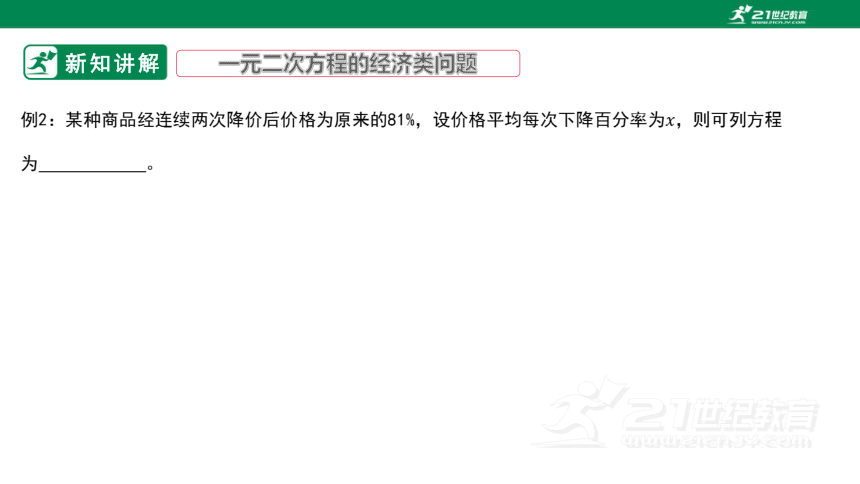
新知讲解
一元二次方程的经济类问题
例1:来自信息产业部的统计数字显示,今年1月至4月份我国手机产量为4000万台,相当于去年全年手机产量的80%,预计到明年年底手机产量达到9800万台。设这两年手机产量平均每年的增长率为,则可以列方程为 。
新知讲解
一元二次方程的经济类问题
例2:某种商品经连续两次降价后价格为原来的81%,设价格平均每次下降百分率为,则可列方程为 。
新知讲解
一元二次方程的经济类问题
例3:要组织一次篮球比赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,则应邀请多少个球队参加比赛?设应邀请,根据题意列方程?
新知讲解
一元二次方程的经济类问题
例4:李明去参加聚会,每两人都互相赠送礼物,他发现共礼物20件,若设有
新知讲解
一元二次方程的经济类问题
例5:某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件。现在要使利润为6125元,每件商品应降价多少元?
新知讲解
一元二次方程的经济类问题
例6:某商场在“五一”小长假期间销售一批衬衫,平均每天可销售20件,每件可获利400元,经调查发现,在一定范围内,衬衫的单价每降10元,每天就可多售出2件衬衫。这种衬衫的单价应降价多少元,才能使商场通过销售这批衬衫平均每天盈利12000元?
新知讲解
一元二次方程的围墙类问题
例1:如图,在足够大的空地上有一段长为木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏。
若=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
新知讲解
一元二次方程的围墙类问题
例2:如图,某农场老板准备建造一个矩形养兔场ABCD,他打算让矩形兔场的一边完全靠着墙MN,墙MN可利用的长度为24米,另外三边用长度为50米的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)。
若要使矩形养兔场的面积为300平方米,则垂直于墙的一边长AB为多少米?
新知讲解
一元二次方程的围墙类问题
例3:如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为。
(1)若矩形鸡舍ABCD面积为150平方米,求篱笆BC的长。
(2)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应的值;若不可以,则说明理由。
新知讲解
一元二次方程的面积类问题
例1:如图,一块长6米宽4米的地毯,为了美观设计了两横两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的。求配色条纹的宽度?
新知讲解
一元二次方程的面积类问题
例2: 如图,某小区规划在一个长的矩形场地上修建两横竖通道,横竖通道的宽度比为2:1,其余部分种植花草,若通道所占面积是整个场地面积的。求横、竖通道的宽各为多少?
新知讲解
一元二次方程的面积类问题
例3:如图,要设计一副宽的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3,如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少
新知讲解
一元二次方程的面积类问题
例4:兴隆镇某养鸡专业户准备建造如图所示的矩形养鸡场,要求长与宽的比为2:1,在养鸡场内,沿前侧内墙保留3宽的走道,其他三侧内墙各保留1宽的走道,当矩形养鸡场长和宽各为多少时,鸡笼区域面积是288?
新知讲解
一元二次方程的体积类问题
例1:长方体木箱的高是8,长比宽多5,体积是52,那么宽是多少?
新知讲解
一元二次方程的体积类问题
例2:如图,有一块矩形铁皮,长它的四角各切去一个同样大小的正方形,然后将四周突出部分折起,就能制作成一个无盖的方盒,如果制成的无盖方盒的底面积为3600制成的方盒的体积是多少
新知讲解
一元二次方程的体积类问题
例3:一个圆柱的底面半径为R若它的高不变,将底面半径增加了体积相应增加了,则R= 。
新知讲解
一元二次方程的体积类问题
例4:如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计)。若长方形纸板边长分别为,且折成的长方体盒子表面积是950,求此时长方体盒子的体积。
一元二次方程的应用
人教版九年级上册
教学目标
新知讲解
一元二次方程的经济类问题
例1:来自信息产业部的统计数字显示,今年1月至4月份我国手机产量为4000万台,相当于去年全年手机产量的80%,预计到明年年底手机产量达到9800万台。设这两年手机产量平均每年的增长率为,则可以列方程为 。
新知讲解
一元二次方程的经济类问题
例2:某种商品经连续两次降价后价格为原来的81%,设价格平均每次下降百分率为,则可列方程为 。
新知讲解
一元二次方程的经济类问题
例3:要组织一次篮球比赛,赛制为单循环形式(每两队之间都赛一场),计划安排15场比赛,则应邀请多少个球队参加比赛?设应邀请,根据题意列方程?
新知讲解
一元二次方程的经济类问题
例4:李明去参加聚会,每两人都互相赠送礼物,他发现共礼物20件,若设有
新知讲解
一元二次方程的经济类问题
例5:某商品的进价为每件40元,当售价为每件60元时,每星期可卖出300件;现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件。现在要使利润为6125元,每件商品应降价多少元?
新知讲解
一元二次方程的经济类问题
例6:某商场在“五一”小长假期间销售一批衬衫,平均每天可销售20件,每件可获利400元,经调查发现,在一定范围内,衬衫的单价每降10元,每天就可多售出2件衬衫。这种衬衫的单价应降价多少元,才能使商场通过销售这批衬衫平均每天盈利12000元?
新知讲解
一元二次方程的围墙类问题
例1:如图,在足够大的空地上有一段长为木栏围成一个矩形菜园ABCD,其中AD≤MN,已知矩形菜园的一边靠墙,另三边一共用了100米木栏。
若=20,所围成的矩形菜园的面积为450平方米,求所利用旧墙AD的长;
新知讲解
一元二次方程的围墙类问题
例2:如图,某农场老板准备建造一个矩形养兔场ABCD,他打算让矩形兔场的一边完全靠着墙MN,墙MN可利用的长度为24米,另外三边用长度为50米的篱笆围成(篱笆正好要全部用完,且不考虑接头的部分)。
若要使矩形养兔场的面积为300平方米,则垂直于墙的一边长AB为多少米?
新知讲解
一元二次方程的围墙类问题
例3:如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为。
(1)若矩形鸡舍ABCD面积为150平方米,求篱笆BC的长。
(2)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应的值;若不可以,则说明理由。
新知讲解
一元二次方程的面积类问题
例1:如图,一块长6米宽4米的地毯,为了美观设计了两横两纵的配色条纹(图中阴影部分),已知配色条纹的宽度相同,所占面积是整个地毯面积的。求配色条纹的宽度?
新知讲解
一元二次方程的面积类问题
例2: 如图,某小区规划在一个长的矩形场地上修建两横竖通道,横竖通道的宽度比为2:1,其余部分种植花草,若通道所占面积是整个场地面积的。求横、竖通道的宽各为多少?
新知讲解
一元二次方程的面积类问题
例3:如图,要设计一副宽的图案,其中有一横一竖的彩条,横、竖彩条的宽度之比为2:3,如果要彩条所占面积是图案面积的19%,问横、竖彩条的宽度各为多少
新知讲解
一元二次方程的面积类问题
例4:兴隆镇某养鸡专业户准备建造如图所示的矩形养鸡场,要求长与宽的比为2:1,在养鸡场内,沿前侧内墙保留3宽的走道,其他三侧内墙各保留1宽的走道,当矩形养鸡场长和宽各为多少时,鸡笼区域面积是288?
新知讲解
一元二次方程的体积类问题
例1:长方体木箱的高是8,长比宽多5,体积是52,那么宽是多少?
新知讲解
一元二次方程的体积类问题
例2:如图,有一块矩形铁皮,长它的四角各切去一个同样大小的正方形,然后将四周突出部分折起,就能制作成一个无盖的方盒,如果制成的无盖方盒的底面积为3600制成的方盒的体积是多少
新知讲解
一元二次方程的体积类问题
例3:一个圆柱的底面半径为R若它的高不变,将底面半径增加了体积相应增加了,则R= 。
新知讲解
一元二次方程的体积类问题
例4:如图,将一张长方形纸板的四个角上分别剪掉2个小正方形和2个小长方形(阴影部分即剪掉的部分),剩余的部分可以折成一个有盖的长方体盒子(纸板的厚度忽略不计)。若长方形纸板边长分别为,且折成的长方体盒子表面积是950,求此时长方体盒子的体积。
同课章节目录
