等比数列1[上学期]
图片预览





文档简介
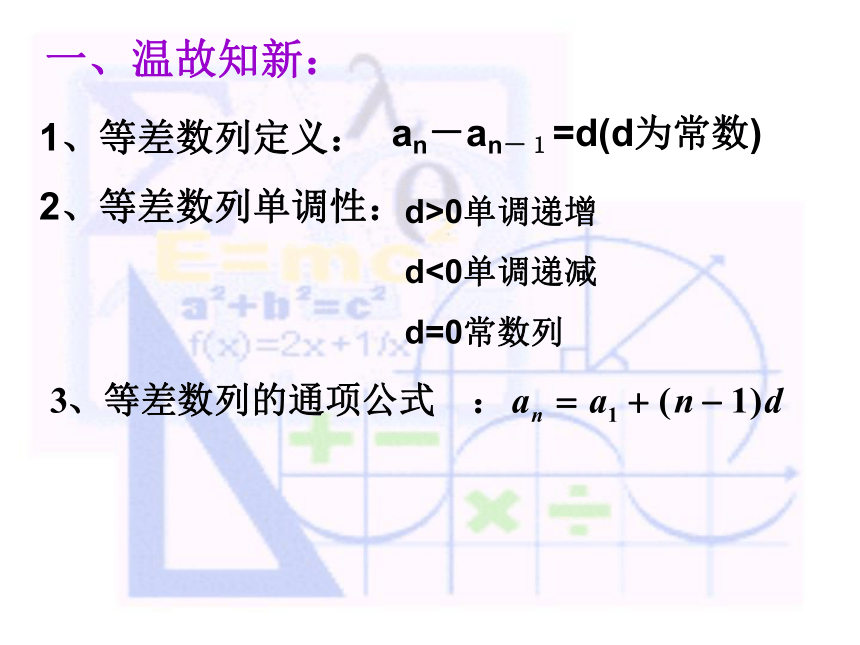
课件16张PPT。等比数列 2006.9.26一、温故知新:1、等差数列定义:
2、等差数列单调性:
an-an-1=d(d为常数)d>0单调递增
d<0单调递减
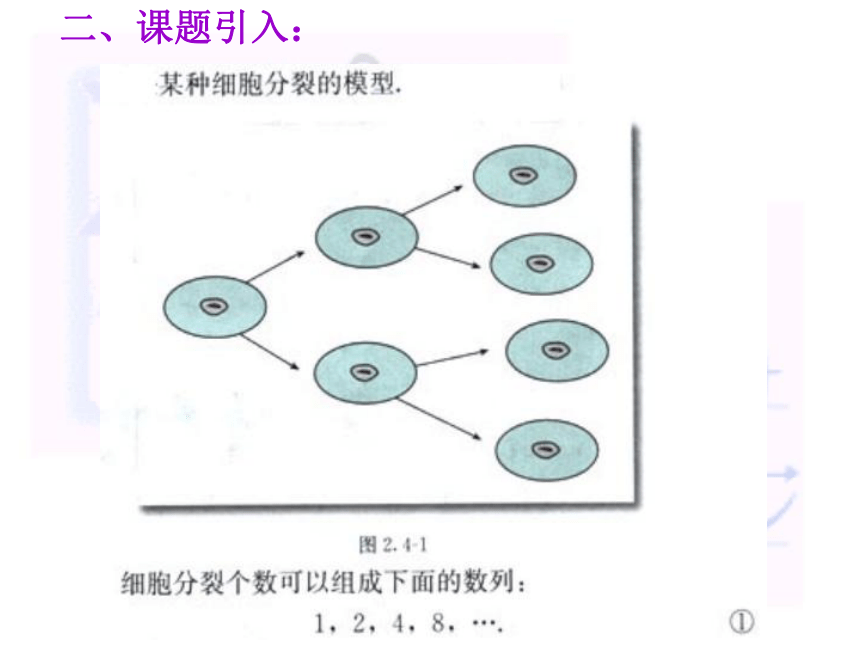
d=0常数列二、课题引入: 一般地,如果一个数列从第二项起每
一项与它的前一项的比等于同一个常数,那
么这个数列就叫做等比数列,这个常数叫做
等比数列的公比,公比通常用字母q表示(q≠0) 。问:数列a, a, a, a, …(a∈R)是否为等比数列?
如果是,a必须满足什么条件?(1) a=0; 它只是等差数列。
(2) a≠0; 它既是等差数列又是等比数列。1.定义:注:对定义的认识1.等比数列的首项不为0, 即a1≠0。
2.等比数列的每一项都不为0,即an≠0。
3.公比不为0,即q≠0。数学语言:an+1:an=q (q≠0的常数)。2.由定义归纳通项公式问:如何用a1和q表示第n项an
a2/a1=q
a3/a2=q
a4/a3=q
…
an/an-1=q其中,a1与q均不为0。由于当n=1时上面等式两边均为a1,
即等式也成立,说明上面公式当n∈N*时都成立,因此它
就是等比数列{an}的通项公式。这n-1个式子相乘得an/a1=qn-1
所以 an=a1qn-1
1.叠乘法(累乘法)
a2=a1q
a3=a2q=a1q2
a4=a3q=a1q3
…
an=a1qn-12.不完全归纳法等比数列的通项公式:
an=a1qn-1
(n∈N﹡,q≠0)特别地,等比数列{an}中,a1≠0,q≠0若数列{an}的首项是a1=1,公比q=2,则用通项公式表示是: ______an=2 n-1上式还可以写成可见,表示这个等比数列
的各点都在函数
的图象上,如右图所示。 0 1 2 3 4 nan
8
7
6
5
4
3
2
1····例题讲解是例题讲解2.根据右图的框图,写出所打印数列的前5项,并建立数列的递推公式.这个数列是等比数列吗?例3.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.(分析:要求第1项和第2项,必先求公比q.
可利用方程的思想进行求解。)解:用{an} 表示题中公比为q的等比数列,由已知条件,有解得 因此,答:这个数列的第1项与第2项分别是例3.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.课 后 作 业1.(3)(4)组A思考P59练习第3,4题.
2、等差数列单调性:
an-an-1=d(d为常数)d>0单调递增
d<0单调递减
d=0常数列二、课题引入: 一般地,如果一个数列从第二项起每
一项与它的前一项的比等于同一个常数,那
么这个数列就叫做等比数列,这个常数叫做
等比数列的公比,公比通常用字母q表示(q≠0) 。问:数列a, a, a, a, …(a∈R)是否为等比数列?
如果是,a必须满足什么条件?(1) a=0; 它只是等差数列。
(2) a≠0; 它既是等差数列又是等比数列。1.定义:注:对定义的认识1.等比数列的首项不为0, 即a1≠0。
2.等比数列的每一项都不为0,即an≠0。
3.公比不为0,即q≠0。数学语言:an+1:an=q (q≠0的常数)。2.由定义归纳通项公式问:如何用a1和q表示第n项an
a2/a1=q
a3/a2=q
a4/a3=q
…
an/an-1=q其中,a1与q均不为0。由于当n=1时上面等式两边均为a1,
即等式也成立,说明上面公式当n∈N*时都成立,因此它
就是等比数列{an}的通项公式。这n-1个式子相乘得an/a1=qn-1
所以 an=a1qn-1
1.叠乘法(累乘法)
a2=a1q
a3=a2q=a1q2
a4=a3q=a1q3
…
an=a1qn-12.不完全归纳法等比数列的通项公式:
an=a1qn-1
(n∈N﹡,q≠0)特别地,等比数列{an}中,a1≠0,q≠0若数列{an}的首项是a1=1,公比q=2,则用通项公式表示是: ______an=2 n-1上式还可以写成可见,表示这个等比数列
的各点都在函数
的图象上,如右图所示。 0 1 2 3 4 nan
8
7
6
5
4
3
2
1····例题讲解是例题讲解2.根据右图的框图,写出所打印数列的前5项,并建立数列的递推公式.这个数列是等比数列吗?例3.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.(分析:要求第1项和第2项,必先求公比q.
可利用方程的思想进行求解。)解:用{an} 表示题中公比为q的等比数列,由已知条件,有解得 因此,答:这个数列的第1项与第2项分别是例3.一个等比数列的第3项和第4项分别是12和18,求它的第1项和第2项.课 后 作 业1.(3)(4)组A思考P59练习第3,4题.
