2022--2023学年北师大版八年级数学上册3.2 平面直角坐标系 同步复习小测 (Word版含答案)
文档属性
| 名称 | 2022--2023学年北师大版八年级数学上册3.2 平面直角坐标系 同步复习小测 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 206.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 11:12:22 | ||
图片预览




文档简介
3.2平面直角坐标系---八年级同步复习小测(基础复习+能力提升)
【北师大版】
【基础复习】
一、单选题
1.在x轴上到点A(3,0)的距离为4的点一定是( )
A.(7,0) B.(-1,0)
C.(7,0) 和(-1,0) D.以上都不对
2.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,2) B.(2,0) C.(4,0) D.(0,﹣4)
3.已知点,则和满足( )
A.P1P2//x轴 B. C.P1P2//y轴 D.
4.一只跳蚤在第一象限及 、 轴上跳动,第一次它从原点跳到 ,然后按图中箭头所示方向跳动 ……,每次跳一个单位长度,则第2020次跳到点( )
A. B. C. D.
二、填空题
5.在平面直角坐标系中,已知点M(m-1,2m+3)在y轴上,则m= .
6.已知点 在 轴上,则点 的坐标为 .
7.已知在平面直角坐标系中,点M的坐标为,点N的坐标为,若轴,则点M的坐标为 .
8.如图,在平面直角坐标系中,第一次将 变换成 ,第二次将 变换成 ,第三次将 变换成 , ,将 进行n次变换,得到 ,观察每次变换中三角形顶点坐标有何变化,找出规律,推测 的坐标是 , 的坐标是 .
三、解答题
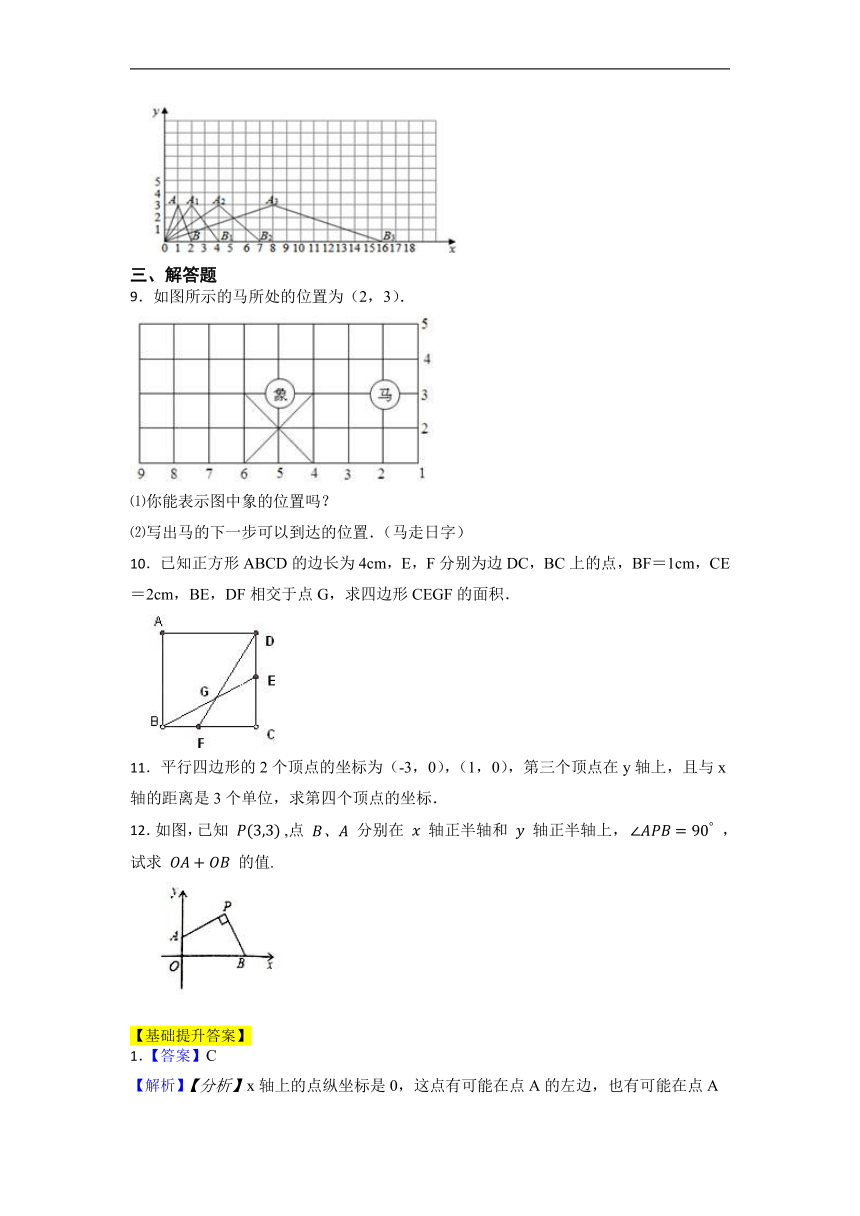
9.如图所示的马所处的位置为(2,3).
⑴你能表示图中象的位置吗?
⑵写出马的下一步可以到达的位置.(马走日字)
10.已知正方形ABCD的边长为4cm,E,F分别为边DC,BC上的点,BF=1cm,CE=2cm,BE,DF相交于点G,求四边形CEGF的面积.
11.平行四边形的2个顶点的坐标为(-3,0),(1,0),第三个顶点在y轴上,且与x轴的距离是3个单位,求第四个顶点的坐标.
12.如图,已知 ,点 分别在 轴正半轴和 轴正半轴上, ,试求 的值.
【基础提升答案】
1.【答案】C
【解析】【分析】x轴上的点纵坐标是0,这点有可能在点A的左边,也有可能在点A的右边.
【解答】∵3+4=7,3-4=-1,
∴点的横坐标是7或-1,
∴在x轴上到点A(3,0)的距离为4的点为(7,0)和(-1,0).
故选C.
【点评】本题考查了点到坐标轴距离的含义,到x轴上到一定点等于定长的点的有2个.
2.【答案】B
【解析】【解答】解:∵点P(m+3,m+1)在x轴上,
∴y=0,
∴m+1=0,
解得:m=﹣1,
∴m+3=﹣1+3=2,
∴点P的坐标为(2,0).
故选:B.
【分析】根据点P在x轴上,即y=0,可得出m的值,从而得出点P的坐标.
3.【答案】C
【解析】【解答】解:∵P1( 6,2),P2( 6, 2),
∴两个点关于x轴对称,与y轴平行,
故答案为:C.
【分析】根据点P1、P2的横坐标相同,纵坐标相反可得两个点关于x轴对称,与y轴平行,从而得解。
4.【答案】D
【解析】【解答】解:跳蚤运动的速度是每秒运动一个单位长度, 用的次数是 次,到 是第 次,到 是第 次,到 是第 次,到 是第 次,到 第 次,依此类推,到 是第2025次. ,
故第2018次时跳蚤所在位置的坐标是 .
故答案为:D.
【分析】根据跳蚤运动的速度确定: 用的次数是 次,到 是第 次,到 是第 次,到 是第 次,到 是第 次,到 是第 次,依此类推,到 是第2025次,后退5次可得2020次所对应的坐标.
5.【答案】1
【解析】【解答】解:由 在 轴上,
解得:m=1
故答案为:1
【分析】由 轴上的点的横坐标为 ,列方程求解即可.
6.【答案】
【解析】【解答】解: 点 在 轴上
解得
故答案为: .
【分析】根据y轴上点的横坐标为0建立方程,求出m值即可求出结论.
7.【答案】(28,12)
【解析】【解答】∵点M的坐标为,点N的坐标为,轴,
∴,
∴,
∴,
∴点M的坐标为(28,12),
故答案为:(28,12).
【分析】根据轴可得,则,即可求出点M的坐标。
8.【答案】;
【解析】【解答】解: ,
的横坐标为 , 纵坐标都为3,
,即
故答案为: ; .
【分析】根据图形写出点A系列的坐标,根据具体数值找到规律即可.
9.【答案】解:(1)象的位置(5,3);
(2)马的下一步可到达位置(1,1)(3,1)(4,2)(1,5)(3,5)(4,4)
【解析】【解答】(1)由马所处的位置为(2,3),知横向的为横坐标,纵向的为纵坐标,从而确定图中象的位置;
(2)根据马走“日”字,先确定马到达是点,再用坐标表示位置.
(1)象的位置(5,3);
(2)马的下一步可到达位置(1,1)(3,1)(4,2)(1,5)(3,5)(4,4)
【分析】解决此类问题需要先确定原点的位置,再求未知点的位置.或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
10.【答案】解:以B点为坐标原点建立坐标系,如下图:由题意可得几个点的坐标A(0,4),B(0,0),C(4,0),D(4,4),E(4,2),F(1,0).设BE所在直线的解析式是y=kx,因为BE所在直线经过E点,因此有4k=2,k= ,因此BE所在直线的解析式是y= x(1),同理可得出DF所在直线的解析式是y= (x-1)(2),联立(1)(2)可解得点G的坐标为( , ).故可求四边形CEGF的面积S=S△BCE-S△BFG= ×4×2- ×1× = .
【解析】【分析】以B点为坐标原点建立坐标系,根据已知条件BF=1cm,CE=2cm可的A,B,C,D,E,F六个点的坐标,四边形CEGF的面积=BCE的面积-BFG的面积即可求解。
11.【答案】解:①当第三个点C1在y轴正半轴时:
AC1为对角线时,第四个点为(-4,3);
AB为对角线时,第四个点为(-2,-3);
BC1为对角线时,第四个点为(4,3).
②当第三个点C2在y轴负半轴时:
AC2为对角线时,第四个点为(-4,-3);
AB为对角线时,第四个点为(-2,3);
BC2为对角线时,第四个点为(4,-3).
即第4个顶点坐标为:(4,3),(-4,3),(-2,-3),或(4,-3),(-4,-3),(-2,3).
【解析】【分析】先分C点在y轴的正半轴还是负半轴进行讨论,①若C点在y轴的正半轴,再分AC、AB、BC为对角线三种情况求第四个点坐标,②若C点在y轴的负半轴,同样再分AC、AB、BC为对角线三种情况求第四个点坐标。
12.【答案】解:过 作 轴于 轴于,
,
,
轴 轴,
,
,
则四边形 是正方形,
,
,
,
,
在 和 中
,
,
,
故答案为: .
【解析】【分析】 过作轴于轴于点N,可得四边形PMON是正方形,从而可得OM=ON=PN=PM=3,∠APB=∠MON=90°,继而可得∠APM=∠BPN,根据“ASA”可证△APM≌△BPN,可得AM=BN,由OA+OB=ON+OM即可求出结论.
【能力提升】
一、单选题
1.若点P在第二象限内,点P到x轴的距离是5,到y轴的距离是2,则点P的坐标为( )
A.(-5,2) B.(-5,-2) C.(-2,5) D.(-2,-5)
2.在平面直角坐标系中,下列说法正确的是( )
A.点P(3,2)到x轴的距离是3
B.若ab=0,则点P(a,b)表示原点
C.若A(2,-2),B(2,2),则直线AB∥x轴
D.第三象限内点的坐标,横、纵坐标同号
3.已知直角坐标系内有一点M(a,b),且ab=0,则点M的位置一定在( )
A.原点上 B.x轴上 C.y轴上 D.坐标轴上
4.平面直角坐标系中,已知点A(-3,2),B(x,y),且AB//x轴,若点B到y轴的距离是到x轴距离的2倍,则点B的坐标为( ).
A.(4,2)或(-4, 2) B.(-4,2)或 (-4,-2)
C.(4,2)或 (4,-2) D.(-4,-2)或(4,-2)
二、填空题
5.矩形OABC在坐标系中的位置如图,点B坐标为(3,-2),则矩形的面积等于
6.如图,已知OA=OB,BC⊥AC于点C,点C对应的数是-2,AC=1,那么数轴上点B所表示的数是
7.在平面直角坐标系中,点 在第二象限,且该点到 轴与到 轴的距离相等,则 点坐标为 .
8.在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x, )的纵坐标满足 ,那么称点Q为点P的“关联点”.请写出点(3,5)的“关联点”的坐标 ;如果点P(x,y)的关联点Q坐标为(-2,3),则点P的坐标为 .
三、解答题
9.在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系?顺次连接A,B,C,D四点,求四边形ABCD的面积.
10.对于边长为4的等边三角形 ,请建立适当的平面直角坐标系,并写出各个顶点的坐标.
11.已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积.
12.建立平面直角坐标系,依次描出点A(-2,0),B(0,-3),C(-3,-5),连接AB、BC、CA.求△ABC的面积.
【能力提升答案】
1.【答案】C
【解析】【解答】解:∵点P在第二象限内,点P到x轴的距离是5,到y轴的距离是2,
∴点P的横坐标为-2,纵坐标为5,
∴点P的坐标为(-2,5).
故答案为:C.
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值,据此解答即可.
2.【答案】D
【解析】【解答】A.点P(3,2) 到x轴的距离是2,故本选项不符合题意.
B.当ab=0时,点P(a,b)表示原点或坐标轴上的点,故本选项不符合题意.
C.当A(2,-2) ,B(2,2)时,直线AB∥y轴,故本选项不符合题意.
D.第三象限内点的坐标,横、纵坐标都是负数,即同号,故本选项符合题意
故答案为:D.
【分析】根据点的坐标的几何意义,逐项判断即可。
3.【答案】D
【解析】【分析】根据坐标轴上的点的特征:至少一个坐标为0解答.
【解答】若ab=0,则a=0,或b=0,或a,b均为0.
当a=0,M在y轴上;
当b=0,M在x轴上;
当a,b均为0,M在原点;
即点M在坐标轴上.
故选D.
【点评】本题主要考查了点在坐标轴上时点的符号特点,注意考虑问题要全面,坐标轴上的点的特点要记清
4.【答案】A
【解析】【解答】解:∵AB//x,
∴B点的纵坐标为2,
∴B点到x轴的距离为2,
∵点B到y轴的距离是到x轴距离的2倍,
∴ ,得 ,
∴点B的坐标为(4,2)或(-4, 2),
故答案为:A.
【分析】由平行于x轴的直线上所有点的纵坐标相同,可知A、B两点的纵坐标都是2,根据一个点到x轴的距离等于其纵坐标的绝对值,到y轴的距离等于其横坐标的绝对值,把那个结合点B到y轴的距离是到x轴距离的2倍可求解.
5.【答案】6
【解析】【解答】解:∵点B坐标为(3,-2),
∴矩形的长为3,宽为2,
则矩形的面积=3×2=6.
故答案为6.
【分析】根据点B的坐标可得矩形的长为3,宽为2,再利用矩形的面积公式求解即可。
6.【答案】
【解析】【解答】解:由图可知,OC=2,作AC⊥OC,垂足为C,
∵AC=1,
∴OB=OA= ,
∵B在x的负半轴上,
∴数轴上点B所表示的数是- .
故答案为:- .
【分析】先利用勾股定理求出BO的长,再根据OB=OA及数轴上两点之间的距离公式即可表示出点B的数。
7.【答案】
【解析】【解答】解:∵点 在第二象限,且该点到x、y轴的距离相等,
∴ ,
解得: .
则 , ,
故 点坐标为: .
故答案为: .
【分析】根据第二象限的点的横坐标是负数,纵坐标是正数,在列出方程求解即可。
8.【答案】(3,2);(-2,1)或(-2,-5)
【解析】【解答】解:∵3<5,根据关联点的定义,
∴y′=5-3=2,
点(3,5)的“关联点”的坐标(3,2);
∵点P(x,y)的关联点Q坐标为(-2,3),
∴y′=y-x=3或x-y=3,
即y-(-2)=3或(-2)-y=3,
解得:y=1或y=-5,
∴点P的坐标为(-2,1)或(-2,-5).
故答案为:(3,2);(-2,1)或(-2,-5).
【分析】根据关联点的定义,可得答案.
9.【答案】解:(1)画出图形直接得到AB∥x轴,DC∥x轴,所以AB∥CD;(2)S=4×3=12
【解析】【分析】先在平面直角坐标系中描点、连线,画出图形。然后证明这是一个平行四边形,从而求出平行四边形ABCD的面积=底×高。
10.【答案】解:如图,以边BC所在的直线为x轴,以边BC的中垂线为y轴建立直角坐标系。
由等边三角形的性质可知AO= ,
顶点A,B,C的坐标分别为:
A(0, ),B(-2,0),C(2,0) (每个坐标各2分)
(此题答案不唯一)
【解析】【分析】 如图,以边BC所在的直线为x轴,以边BC的中垂线为y轴建立直角坐标系 ,根据等腰三角形的三线合一得出BO=OC=2,在Rt△ABO中,根据勾股定理算出AO的长,进而根据纵坐标轴上的点的坐标特点即可写出A,B,C三点的坐标.
11.【答案】解:∵AB边上的高为4,
∴点C的纵坐标为4或﹣4,
∵第三个顶点C的横坐标为﹣1,
∴点C的坐标为(﹣1,4)或(﹣1,﹣4);
∵A(﹣4,0),B(2,0),
∴AB=2﹣(﹣4)=2+4=6,
∴△ABC的面积= ×6×4=12.
【解析】【分析】根据点C到AB的距离分点C在x轴上方和下方两种情况写出点C的坐标,再根据三角形的面积公式列式计算即可得解.
12.【答案】解:如图所示,
S△ABC=S矩形CEOD﹣S△ACD﹣S△CEB﹣S△AOB
=3×5﹣ ×1×5﹣ ×2×3﹣ ×2×3
=15﹣8.5
=6.5.
【解析】【分析】在平面直角坐标系中连接AB、BC、CA,构成三角形,利用“割补法”求△ABC的面积.
【北师大版】
【基础复习】
一、单选题
1.在x轴上到点A(3,0)的距离为4的点一定是( )
A.(7,0) B.(-1,0)
C.(7,0) 和(-1,0) D.以上都不对
2.如果点P(m+3,m+1)在x轴上,则点P的坐标为( )
A.(0,2) B.(2,0) C.(4,0) D.(0,﹣4)
3.已知点,则和满足( )
A.P1P2//x轴 B. C.P1P2//y轴 D.
4.一只跳蚤在第一象限及 、 轴上跳动,第一次它从原点跳到 ,然后按图中箭头所示方向跳动 ……,每次跳一个单位长度,则第2020次跳到点( )
A. B. C. D.
二、填空题
5.在平面直角坐标系中,已知点M(m-1,2m+3)在y轴上,则m= .
6.已知点 在 轴上,则点 的坐标为 .
7.已知在平面直角坐标系中,点M的坐标为,点N的坐标为,若轴,则点M的坐标为 .
8.如图,在平面直角坐标系中,第一次将 变换成 ,第二次将 变换成 ,第三次将 变换成 , ,将 进行n次变换,得到 ,观察每次变换中三角形顶点坐标有何变化,找出规律,推测 的坐标是 , 的坐标是 .
三、解答题
9.如图所示的马所处的位置为(2,3).
⑴你能表示图中象的位置吗?
⑵写出马的下一步可以到达的位置.(马走日字)
10.已知正方形ABCD的边长为4cm,E,F分别为边DC,BC上的点,BF=1cm,CE=2cm,BE,DF相交于点G,求四边形CEGF的面积.
11.平行四边形的2个顶点的坐标为(-3,0),(1,0),第三个顶点在y轴上,且与x轴的距离是3个单位,求第四个顶点的坐标.
12.如图,已知 ,点 分别在 轴正半轴和 轴正半轴上, ,试求 的值.
【基础提升答案】
1.【答案】C
【解析】【分析】x轴上的点纵坐标是0,这点有可能在点A的左边,也有可能在点A的右边.
【解答】∵3+4=7,3-4=-1,
∴点的横坐标是7或-1,
∴在x轴上到点A(3,0)的距离为4的点为(7,0)和(-1,0).
故选C.
【点评】本题考查了点到坐标轴距离的含义,到x轴上到一定点等于定长的点的有2个.
2.【答案】B
【解析】【解答】解:∵点P(m+3,m+1)在x轴上,
∴y=0,
∴m+1=0,
解得:m=﹣1,
∴m+3=﹣1+3=2,
∴点P的坐标为(2,0).
故选:B.
【分析】根据点P在x轴上,即y=0,可得出m的值,从而得出点P的坐标.
3.【答案】C
【解析】【解答】解:∵P1( 6,2),P2( 6, 2),
∴两个点关于x轴对称,与y轴平行,
故答案为:C.
【分析】根据点P1、P2的横坐标相同,纵坐标相反可得两个点关于x轴对称,与y轴平行,从而得解。
4.【答案】D
【解析】【解答】解:跳蚤运动的速度是每秒运动一个单位长度, 用的次数是 次,到 是第 次,到 是第 次,到 是第 次,到 是第 次,到 第 次,依此类推,到 是第2025次. ,
故第2018次时跳蚤所在位置的坐标是 .
故答案为:D.
【分析】根据跳蚤运动的速度确定: 用的次数是 次,到 是第 次,到 是第 次,到 是第 次,到 是第 次,到 是第 次,依此类推,到 是第2025次,后退5次可得2020次所对应的坐标.
5.【答案】1
【解析】【解答】解:由 在 轴上,
解得:m=1
故答案为:1
【分析】由 轴上的点的横坐标为 ,列方程求解即可.
6.【答案】
【解析】【解答】解: 点 在 轴上
解得
故答案为: .
【分析】根据y轴上点的横坐标为0建立方程,求出m值即可求出结论.
7.【答案】(28,12)
【解析】【解答】∵点M的坐标为,点N的坐标为,轴,
∴,
∴,
∴,
∴点M的坐标为(28,12),
故答案为:(28,12).
【分析】根据轴可得,则,即可求出点M的坐标。
8.【答案】;
【解析】【解答】解: ,
的横坐标为 , 纵坐标都为3,
,即
故答案为: ; .
【分析】根据图形写出点A系列的坐标,根据具体数值找到规律即可.
9.【答案】解:(1)象的位置(5,3);
(2)马的下一步可到达位置(1,1)(3,1)(4,2)(1,5)(3,5)(4,4)
【解析】【解答】(1)由马所处的位置为(2,3),知横向的为横坐标,纵向的为纵坐标,从而确定图中象的位置;
(2)根据马走“日”字,先确定马到达是点,再用坐标表示位置.
(1)象的位置(5,3);
(2)马的下一步可到达位置(1,1)(3,1)(4,2)(1,5)(3,5)(4,4)
【分析】解决此类问题需要先确定原点的位置,再求未知点的位置.或者直接利用坐标系中的移动法则“右加左减,上加下减”来确定坐标.
10.【答案】解:以B点为坐标原点建立坐标系,如下图:由题意可得几个点的坐标A(0,4),B(0,0),C(4,0),D(4,4),E(4,2),F(1,0).设BE所在直线的解析式是y=kx,因为BE所在直线经过E点,因此有4k=2,k= ,因此BE所在直线的解析式是y= x(1),同理可得出DF所在直线的解析式是y= (x-1)(2),联立(1)(2)可解得点G的坐标为( , ).故可求四边形CEGF的面积S=S△BCE-S△BFG= ×4×2- ×1× = .
【解析】【分析】以B点为坐标原点建立坐标系,根据已知条件BF=1cm,CE=2cm可的A,B,C,D,E,F六个点的坐标,四边形CEGF的面积=BCE的面积-BFG的面积即可求解。
11.【答案】解:①当第三个点C1在y轴正半轴时:
AC1为对角线时,第四个点为(-4,3);
AB为对角线时,第四个点为(-2,-3);
BC1为对角线时,第四个点为(4,3).
②当第三个点C2在y轴负半轴时:
AC2为对角线时,第四个点为(-4,-3);
AB为对角线时,第四个点为(-2,3);
BC2为对角线时,第四个点为(4,-3).
即第4个顶点坐标为:(4,3),(-4,3),(-2,-3),或(4,-3),(-4,-3),(-2,3).
【解析】【分析】先分C点在y轴的正半轴还是负半轴进行讨论,①若C点在y轴的正半轴,再分AC、AB、BC为对角线三种情况求第四个点坐标,②若C点在y轴的负半轴,同样再分AC、AB、BC为对角线三种情况求第四个点坐标。
12.【答案】解:过 作 轴于 轴于,
,
,
轴 轴,
,
,
则四边形 是正方形,
,
,
,
,
在 和 中
,
,
,
故答案为: .
【解析】【分析】 过作轴于轴于点N,可得四边形PMON是正方形,从而可得OM=ON=PN=PM=3,∠APB=∠MON=90°,继而可得∠APM=∠BPN,根据“ASA”可证△APM≌△BPN,可得AM=BN,由OA+OB=ON+OM即可求出结论.
【能力提升】
一、单选题
1.若点P在第二象限内,点P到x轴的距离是5,到y轴的距离是2,则点P的坐标为( )
A.(-5,2) B.(-5,-2) C.(-2,5) D.(-2,-5)
2.在平面直角坐标系中,下列说法正确的是( )
A.点P(3,2)到x轴的距离是3
B.若ab=0,则点P(a,b)表示原点
C.若A(2,-2),B(2,2),则直线AB∥x轴
D.第三象限内点的坐标,横、纵坐标同号
3.已知直角坐标系内有一点M(a,b),且ab=0,则点M的位置一定在( )
A.原点上 B.x轴上 C.y轴上 D.坐标轴上
4.平面直角坐标系中,已知点A(-3,2),B(x,y),且AB//x轴,若点B到y轴的距离是到x轴距离的2倍,则点B的坐标为( ).
A.(4,2)或(-4, 2) B.(-4,2)或 (-4,-2)
C.(4,2)或 (4,-2) D.(-4,-2)或(4,-2)
二、填空题
5.矩形OABC在坐标系中的位置如图,点B坐标为(3,-2),则矩形的面积等于
6.如图,已知OA=OB,BC⊥AC于点C,点C对应的数是-2,AC=1,那么数轴上点B所表示的数是
7.在平面直角坐标系中,点 在第二象限,且该点到 轴与到 轴的距离相等,则 点坐标为 .
8.在平面直角坐标系xOy中,对于点P(x,y),如果点Q(x, )的纵坐标满足 ,那么称点Q为点P的“关联点”.请写出点(3,5)的“关联点”的坐标 ;如果点P(x,y)的关联点Q坐标为(-2,3),则点P的坐标为 .
三、解答题
9.在图中描出A(-4,4),B(0,4),C(2,1),D(-2,1)四个点,线段AB、CD有什么位置关系?顺次连接A,B,C,D四点,求四边形ABCD的面积.
10.对于边长为4的等边三角形 ,请建立适当的平面直角坐标系,并写出各个顶点的坐标.
11.已知三角形ABC的两个顶点坐标为A(﹣4,0),B(2,0),如图,且过这两个点的边上的高为4,第三个顶点的横坐标为﹣1,求顶点C的坐标及三角形的面积.
12.建立平面直角坐标系,依次描出点A(-2,0),B(0,-3),C(-3,-5),连接AB、BC、CA.求△ABC的面积.
【能力提升答案】
1.【答案】C
【解析】【解答】解:∵点P在第二象限内,点P到x轴的距离是5,到y轴的距离是2,
∴点P的横坐标为-2,纵坐标为5,
∴点P的坐标为(-2,5).
故答案为:C.
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的绝对值,到y轴的距离等于横坐标的绝对值,据此解答即可.
2.【答案】D
【解析】【解答】A.点P(3,2) 到x轴的距离是2,故本选项不符合题意.
B.当ab=0时,点P(a,b)表示原点或坐标轴上的点,故本选项不符合题意.
C.当A(2,-2) ,B(2,2)时,直线AB∥y轴,故本选项不符合题意.
D.第三象限内点的坐标,横、纵坐标都是负数,即同号,故本选项符合题意
故答案为:D.
【分析】根据点的坐标的几何意义,逐项判断即可。
3.【答案】D
【解析】【分析】根据坐标轴上的点的特征:至少一个坐标为0解答.
【解答】若ab=0,则a=0,或b=0,或a,b均为0.
当a=0,M在y轴上;
当b=0,M在x轴上;
当a,b均为0,M在原点;
即点M在坐标轴上.
故选D.
【点评】本题主要考查了点在坐标轴上时点的符号特点,注意考虑问题要全面,坐标轴上的点的特点要记清
4.【答案】A
【解析】【解答】解:∵AB//x,
∴B点的纵坐标为2,
∴B点到x轴的距离为2,
∵点B到y轴的距离是到x轴距离的2倍,
∴ ,得 ,
∴点B的坐标为(4,2)或(-4, 2),
故答案为:A.
【分析】由平行于x轴的直线上所有点的纵坐标相同,可知A、B两点的纵坐标都是2,根据一个点到x轴的距离等于其纵坐标的绝对值,到y轴的距离等于其横坐标的绝对值,把那个结合点B到y轴的距离是到x轴距离的2倍可求解.
5.【答案】6
【解析】【解答】解:∵点B坐标为(3,-2),
∴矩形的长为3,宽为2,
则矩形的面积=3×2=6.
故答案为6.
【分析】根据点B的坐标可得矩形的长为3,宽为2,再利用矩形的面积公式求解即可。
6.【答案】
【解析】【解答】解:由图可知,OC=2,作AC⊥OC,垂足为C,
∵AC=1,
∴OB=OA= ,
∵B在x的负半轴上,
∴数轴上点B所表示的数是- .
故答案为:- .
【分析】先利用勾股定理求出BO的长,再根据OB=OA及数轴上两点之间的距离公式即可表示出点B的数。
7.【答案】
【解析】【解答】解:∵点 在第二象限,且该点到x、y轴的距离相等,
∴ ,
解得: .
则 , ,
故 点坐标为: .
故答案为: .
【分析】根据第二象限的点的横坐标是负数,纵坐标是正数,在列出方程求解即可。
8.【答案】(3,2);(-2,1)或(-2,-5)
【解析】【解答】解:∵3<5,根据关联点的定义,
∴y′=5-3=2,
点(3,5)的“关联点”的坐标(3,2);
∵点P(x,y)的关联点Q坐标为(-2,3),
∴y′=y-x=3或x-y=3,
即y-(-2)=3或(-2)-y=3,
解得:y=1或y=-5,
∴点P的坐标为(-2,1)或(-2,-5).
故答案为:(3,2);(-2,1)或(-2,-5).
【分析】根据关联点的定义,可得答案.
9.【答案】解:(1)画出图形直接得到AB∥x轴,DC∥x轴,所以AB∥CD;(2)S=4×3=12
【解析】【分析】先在平面直角坐标系中描点、连线,画出图形。然后证明这是一个平行四边形,从而求出平行四边形ABCD的面积=底×高。
10.【答案】解:如图,以边BC所在的直线为x轴,以边BC的中垂线为y轴建立直角坐标系。
由等边三角形的性质可知AO= ,
顶点A,B,C的坐标分别为:
A(0, ),B(-2,0),C(2,0) (每个坐标各2分)
(此题答案不唯一)
【解析】【分析】 如图,以边BC所在的直线为x轴,以边BC的中垂线为y轴建立直角坐标系 ,根据等腰三角形的三线合一得出BO=OC=2,在Rt△ABO中,根据勾股定理算出AO的长,进而根据纵坐标轴上的点的坐标特点即可写出A,B,C三点的坐标.
11.【答案】解:∵AB边上的高为4,
∴点C的纵坐标为4或﹣4,
∵第三个顶点C的横坐标为﹣1,
∴点C的坐标为(﹣1,4)或(﹣1,﹣4);
∵A(﹣4,0),B(2,0),
∴AB=2﹣(﹣4)=2+4=6,
∴△ABC的面积= ×6×4=12.
【解析】【分析】根据点C到AB的距离分点C在x轴上方和下方两种情况写出点C的坐标,再根据三角形的面积公式列式计算即可得解.
12.【答案】解:如图所示,
S△ABC=S矩形CEOD﹣S△ACD﹣S△CEB﹣S△AOB
=3×5﹣ ×1×5﹣ ×2×3﹣ ×2×3
=15﹣8.5
=6.5.
【解析】【分析】在平面直角坐标系中连接AB、BC、CA,构成三角形,利用“割补法”求△ABC的面积.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
