2022-2023学年人教版八年级数学上册 11.1 与三角形有关的线段 同步测试卷 (Word版含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学上册 11.1 与三角形有关的线段 同步测试卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 537.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 11:34:02 | ||
图片预览




文档简介
11.1 与三角形有关的线段
考点一、三角形三边的关系
知识点:
①三角形任意两边之和大于第三边,b + c > a;
②三角形任意两边之差小于第三边,b - c < a。
理论依据:两点之间线段最短;
判断三条已知线段a、b、c能否组成三角形:
当a最长,且有 b + c > a时,就可构成三角形。
确定三角形第三边的取值范围:|a-b| < c < a+b
相应练习:
1、三角形的三边长分别为2,,5,则x的取值范围是( )
A. B. C. D.
2、△ABC为等腰三角形,周长为7cm,且各边长为整数,则该三角形最长边的长为 cm.
3、已知的两边长a和b满足.
(1)若第三边长为c,求c的取值范围.
(2)若是等腰三角形,求的周长.
4、若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
5、已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.
挑战题:
1、不等边△ABC的两条高的长度分别为4和12,若第三条高也为整数,那么它的长度最大值是
考点二、三角形的高、中线与角平分线
知识点:
1、三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
①锐角三角形的三条高线交于三角形内部一点;
②直角三角形的三条高线交于直角顶点;
③钝角三角形的三条高线所在直线交于三角形外部一点。
三条高线的交点称为“垂心”。
2、三角形的中线
连接三角形一个顶点与它对边中点的线段叫做三角形的中线。
三角形三条中线交于三角形内部一点,这一点叫做“三角形的重心”;
重要结论:①BD=CD=BC
②S△ABD=S△ADC=S△ABC
③C△ABD-C△ADC=AB-AC
3、三角形的角平分线
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
三角形三条角平分线交于三角形内部一点,这一点叫做“三角形的内心”。
相应练习:
1、如图, 于点D, 于点C, 于点F,下列关于高的说法错误的是( )
A.在 中, 是 边上的高
B.在 中, 是 边上的高
C.在 中, 是 边上的高
D.在 中, 是 边上的高
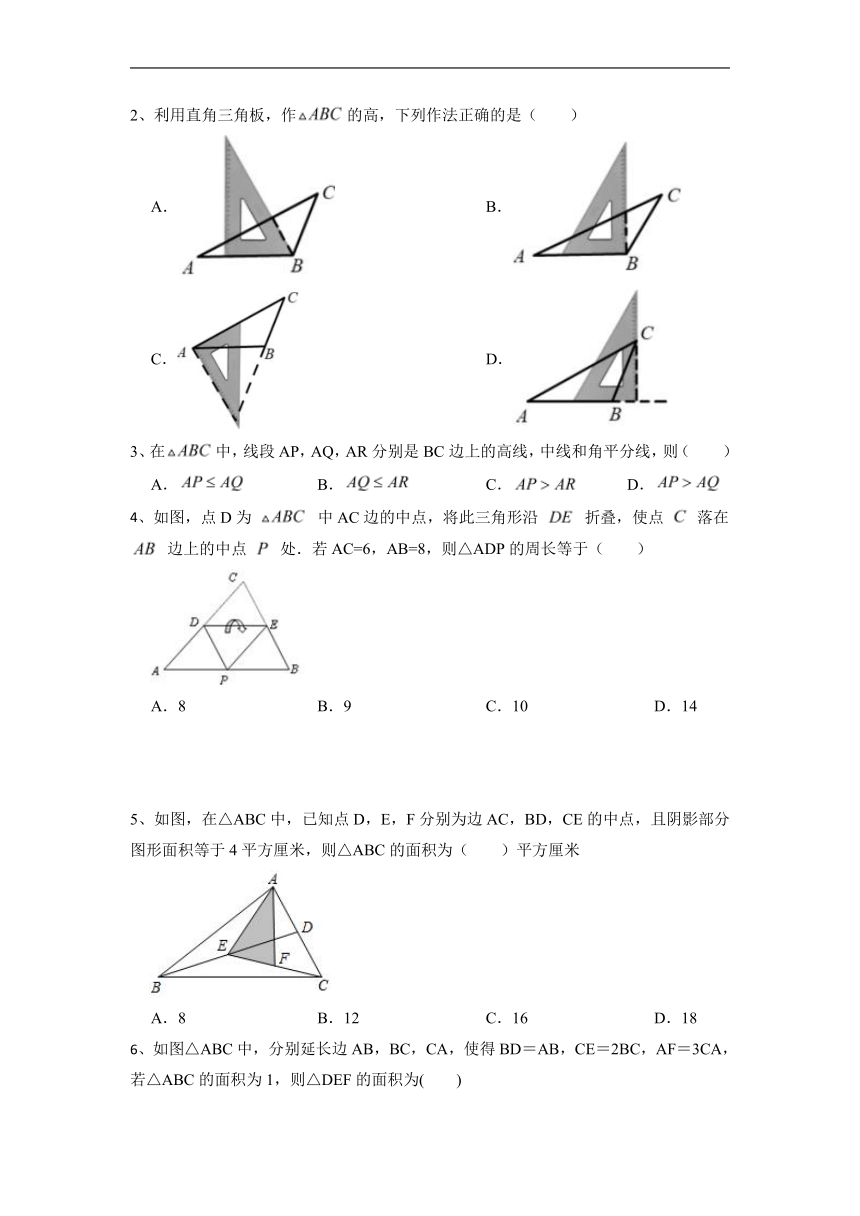
2、利用直角三角板,作的高,下列作法正确的是( )
A. B.
C. D.
3、在中,线段AP,AQ,AR分别是BC边上的高线,中线和角平分线,则( )
A. B. C. D.
4、如图,点D为 中AC边的中点,将此三角形沿 折叠,使点 落在 边上的中点 处.若AC=6,AB=8,则△ADP的周长等于( )
A.8 B.9 C.10 D.14
5、如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
6、如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )
A.12 B.14 C.16 D.18
7、如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的有( )个①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A.1 B.2 C.3 D.4
8、如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为 .如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是 .
9、如图,中,BE为AC边上的高,CD平分,CD、BE相交于点F.若,,求的度数.
10、如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数.
11、如图,在△ABC中,AB>AC,AD是中线,将三角形的周长分为15cm和12cm两部分AB+AC=21,求AB、AC的长.
12、如图,在 中, , 边上的高 , 为 边上任一点, 于点 , 于点 ,求 的值.
挑战题:
1、如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD,AE相交于F,已知BD=4AD,设△ABC的面积为S,△CEF的面积为S1,△ADF的面积为S2,则 的值为( )
A. B. C. D.
考点三、三角形的稳定性
知识点:
1. 三角形具有稳定性。
2. 四边形及多边形不具有稳定性。
相应练习:
1、人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间线段最短 B.三角形的稳定性
C.两点确定一条直线 D.垂线段最短
2、如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
3、小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理.
答案解析:
考点一、三角形三边的关系
1、【答案】D
【解析】【解答】解: 三角形的三边长分别为2,,5,
由①得:
由②得:
所以:
所以x的取值范围是
故答案为:D.
【分析】三角形两边之和大于第三边,两边之差小于第三边,列出不等式组,据此解答即可.
2、【答案】3
【解析】【解答】解:设腰长为x,则底边为7-2x.
∵7-2x-x<x<7-2x+x,
∴1.75<x<3.5,
∵三边长均为整数,
∴x可取的值为2或3,
故各边的长为2,2,3或3,3,1.
∴该三角形最长边的长为3cm.
故答案为:3.
【分析】设腰长为x,则底边为7-2x,根据三角形的三边关系可得x的范围,结合x为整数可得x的值,进而得到三角形的三边长,据此可得最长边的长.
3、【答案】(1)解:∵,
∴,,
∴,,
第三边长为c,求c的取值范围是:,
即.
(2)解:由(1)得,,,
是等腰三角形,当a为腰时,的周长为:9+9+4=22,
当b为腰时,4+4<9,不能构成三角形,舍去.
【解析】【分析】(1)根据二次根式及偶次幂的非负性,由两个非负数的和为0,则每一个数都等于0,求出a、b的值,再利用三角形的三边关系求出C的范围即可;
(2) 分两种情况:当a为腰、b为底或当b为腰、a为底,据此分别求解即可.
4、【答案】(1)解:根据三角形的三边关系,
,
解得:3<m<5;
(2)解:因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m 2)+(2m+1)+8=3m+7=3×4+7=19.
【解析】【分析】(1)根据三角形三边的关系可得,再求出m的取值范围即可;
(2)根据m的值为整数可得m的值,再利用三角形的周长公式计算即可。
5、【答案】解:∵b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,
∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|
=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)
=(b+c-a-b+c+a-c+a+b-a+b-c
=2b
【解析】【分析】根据三角形的任意两边之和大于第三边,任意两边之差小于第三边及不等式的性质得出 b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,再根据绝对值的意义去掉绝对值的符号,合并同类项即可.
挑战题:
【答案】5
【解析】【解答】解:因为不等边△ABC的两条高的长度分别为4和12,根据面积相等可设 △ABC的两边长为3x,x;
因为 3x×4=12×x(2倍的面积),面积S=6x,
因为知道两条边的假设长度,根据两边之和大于第三边,两边之差小于第三边可得:2x<第三边长度<4x,
因为要求高的最大长度,所以当第三边最短时,在第三边上的高就越长,
S=×第三边的长×高,6x>×2x×高,6x<×4x×高,
∴6>高>3,
∵是不等边三角形,且高为整数,
∴高的最大值为5,
故答案为:5.
【分析】根据 不等边△ABC的两条高的长度分别为4和12, 求解即可。
考点二、三角形的高、中线与角平分线
1、【答案】C
【解析】【解答】解:A、在△ABC中, AD是BC边上的高,该说法正确,故本选项不符合题意;
B、在△GBC 中,CF是BG边上的高,该说法正确,故本选项不符合题意;
C、在△ABC 中,GC不是BC边上的高,该说法错误,故本选项符合题意;
D、在△GBC 中,GC 是BC边上的高,该说法正确,故本选项不符合题意.
故答案为:C.
【分析】过三角形一个顶点向其对边所在的直线引垂线,顶点与垂足间的线段就是三角形的高,利用三角形高线的定义,对各选项逐一判断即可.
2、【答案】D
【解析】【解答】解:A、B、C均不是高线.
故答案为:D.
【分析】利用作高的方法对每个选项一一判断即可。
3、【答案】A
【解析】【解答】解:∵线段AP是BC边上在的高线,
∴根据垂线段最短得:PA≤AQ,PA≤AR.
故答案为:A.
【分析】根据等腰三角形的性质可得底边的高线、中线和角平分线重合,然后结合垂线段最短的性质进行判断.
4、【答案】C
【解析】【解答】解:∵△PDE是△CDE沿DE折叠而来,
∴CD=DP,
∵点D为AC的中点,AC=6
∴CD=DP=AD=3,
∵点P为AB的中点,AB=8,
∴AP= =4,
∴△ADP的周长=AD+DP+AP=3+3+4=10.
故答案为:C.
【分析】根据折叠的性质可得CD=DP,再利用中点的性质可得CD=DP=AD=3,AP= =4,最后利用三角形的周长公式计算即可。
5、【答案】C
【解析】【解答】解:∵F是EC的中点,
∴,
∴,
∵ E是BD的中点 ,
∴,,
∵,
∴,
∴,
故答案为:C.
【分析】根据三角形中线的性质可得,,,再结合,即可得到。
6、【答案】D
【解析】【解答】解:连接AE和CD,
∵BD=AB,
∴S△ABC=S△BCD=1,S△ACD=1+1=2,
∵AF=3AC,
∴FC=4AC,
∴S△FCD=4S△ACD=4×2=8,
同理可以求得:S△ACE=2S△ABC=2,则S△FCE=4S△ACE=4×2=8;
S△DCE=2S△BCD=2×1=2;
∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18.
故答案为:D.
【分析】连接AE和CD, 根据同高三角形的面积之间的关系可得S△ABC=S△BCD=1,S△ACD=2,S△FCD=4S△ACD=8,同理可得:S△ACE=2S△ABC,则S△FCE=4S△ACE,S△DCE=2S△BCD,然后根据S△DEF=S△FCD+S△FCE+S△DCE进行计算.
7、【答案】B
【解析】【解答】解:∵BE是AC边的中线
∴AE=CE
∵∠BAC=90°
∴ ,
∴△ABE的面积=△BCE的面积
故①正确;
∵AD是BC边上的高
∴∠FAG+∠ABC=90°
∵∠BAC=90°
∴∠ABC+∠ACB=90°
∴∠FAG=∠ACB
∵CF是∠ACB的角平分线
∴∠FCB= ∠ACB=∠ACF
∴
故②错误;
∵∠AFG+∠ACF=∠DGC+∠FCB=90°,∠AGF=∠DGC
∴∠AFG=∠AGF
∴AF=AG
故③正确;
根据已知条件无法证明BH=CH
故④错误;
故答案为:B.
【分析】根据三角形中线的性质可得△ABE的面积=△BCE的面积,据此判断①;根据余角的性质可得∠FAG=∠ACB,由角平分线的定义可得∠FCB=∠ACB=∠ACF,即得,据此判断②;根据余角的性质可得∠AFG=∠AGF,可得AF=AG,据此判断③;根据已知条件无法证明BH=CH,据此判断④.
8、【答案】16;
【解析】【解答】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF= BC,EG= AC,FG= AB,
∴EF+FG+EG= (BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为 ×64=16,
以此类推,第n个小三角形的周长是第一个三角形周长的64×( )n-1,
故答案为:16,64×( )n-1.
【分析】根据三角形中位线定理求出△EFG的周长;然后找出规律,第n个小三角形的周长是第一个三角形周长的64×( )n-1。
9、【答案】解:在中,,,
,
平分,
,
为边上的高,
,
.
【解析】【分析】根据三角形的角平分线、中线和高,以及角的运算法则即可得出答案。
10、【答案】解:∵AE是角平分线,∠CAB=50°,
∴ ,
∵∠BOA=120°,
∴ ,
∵BF是角平分线,
∴ ,
∴ ;
∴ ,
∵AD是高,
∴ .
【解析】【分析】根据AE是角平分线,∠CAB=50°,求出 ,再根据∠BOA=120°,利用三角形内角和定理求出∠ABF的度数,再根据BF是角平分线,得出 ,再利用三角形的内角和定理可求出∠AEB的度数,即可求出∠EAD的度数,即可得出结论。
11、【答案】解:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长=AB+BD+AD,
△ACD的周长=AC+CD+AD =AC+BD+AD,
∴△ABD的周长-△ACD的周长=AB-AC=3.
又∵AB+AC=21,
即: ,
解方程组,得,AB=12,AC=9
答:AB和AC的长分别为12cm和9cm.
【解析】【分析】由中线的定义可得BD=CD, 由三角形的周长差可得AB-AC=3. 结合已知可得关于AB、AC的方程组,解方程组可求得AB、AC的长.
12、【答案】解:连接 ,
∵CD⊥AB, , ,
∴ , , ,
∵ ,
∴ ,
又∵ , ,
∴ .
【解析】【分析】连接AP,根据三角形面积的计算公式即可得到PM+PN的值。
挑战题:
【答案】C
【解析】【解答】解:由折叠可知 ,
∴ ,
∴ ,
∴①,
过E作EH⊥AB于H,CM垂直AB交BA的延长线于M,
∴ , ,
∵BD=4AD,
∴ ,
∴②,
①-②得: ,
∵CM⊥AB,
∴ ,
,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为:C.
【分析】先求出 ,再求出 ,最后计算求解即可。
考点三、三角形的稳定性
1、【答案】B
【知识点】三角形的稳定性
【解析】【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加梯子的稳定性.
故答案为:B.
【分析】三角形具有稳定性,据此解答即可.
2、【答案】D
【知识点】三角形的稳定性
【解析】【解答】解:A.若钉在E,H两点之间构成了三角形,能固定窗框,故不符合题意;
B.若钉在A,C两点之间能构成三角形,能固定窗框,故不符合题意;
C.若钉在F,E两点之间能构成三角形,能固定窗框,故不符合题意;
D.若钉在E,G两点之间不能构成三角形,不能固定窗框,故符合题意;
故答案为:D.
【分析】利用三角形的定义判断求解即可。
3、【答案】解:如图所示:
【知识点】三角形的稳定性
【解析】【分析】 根据三角形具有稳定性,主要是应用了三角形的稳定性.
考点一、三角形三边的关系
知识点:
①三角形任意两边之和大于第三边,b + c > a;
②三角形任意两边之差小于第三边,b - c < a。
理论依据:两点之间线段最短;
判断三条已知线段a、b、c能否组成三角形:
当a最长,且有 b + c > a时,就可构成三角形。
确定三角形第三边的取值范围:|a-b| < c < a+b
相应练习:
1、三角形的三边长分别为2,,5,则x的取值范围是( )
A. B. C. D.
2、△ABC为等腰三角形,周长为7cm,且各边长为整数,则该三角形最长边的长为 cm.
3、已知的两边长a和b满足.
(1)若第三边长为c,求c的取值范围.
(2)若是等腰三角形,求的周长.
4、若△ABC的三边长分别为m-2,2m+1,8.
(1)求m的取值范围;
(2)若△ABC的三边均为整数,求△ABC的周长.
5、已知a、b、c是三角形三边长,试化简:|b+c﹣a|+|b﹣c﹣a|+|c﹣a﹣b|﹣|a﹣b+c|.
挑战题:
1、不等边△ABC的两条高的长度分别为4和12,若第三条高也为整数,那么它的长度最大值是
考点二、三角形的高、中线与角平分线
知识点:
1、三角形的高
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形的高。
①锐角三角形的三条高线交于三角形内部一点;
②直角三角形的三条高线交于直角顶点;
③钝角三角形的三条高线所在直线交于三角形外部一点。
三条高线的交点称为“垂心”。
2、三角形的中线
连接三角形一个顶点与它对边中点的线段叫做三角形的中线。
三角形三条中线交于三角形内部一点,这一点叫做“三角形的重心”;
重要结论:①BD=CD=BC
②S△ABD=S△ADC=S△ABC
③C△ABD-C△ADC=AB-AC
3、三角形的角平分线
三角形一个角的平分线与它的对边相交,这个角的顶点与交点之间的线段叫做三角形的角平分线。
三角形三条角平分线交于三角形内部一点,这一点叫做“三角形的内心”。
相应练习:
1、如图, 于点D, 于点C, 于点F,下列关于高的说法错误的是( )
A.在 中, 是 边上的高
B.在 中, 是 边上的高
C.在 中, 是 边上的高
D.在 中, 是 边上的高
2、利用直角三角板,作的高,下列作法正确的是( )
A. B.
C. D.
3、在中,线段AP,AQ,AR分别是BC边上的高线,中线和角平分线,则( )
A. B. C. D.
4、如图,点D为 中AC边的中点,将此三角形沿 折叠,使点 落在 边上的中点 处.若AC=6,AB=8,则△ADP的周长等于( )
A.8 B.9 C.10 D.14
5、如图,在△ABC中,已知点D,E,F分别为边AC,BD,CE的中点,且阴影部分图形面积等于4平方厘米,则△ABC的面积为( )平方厘米
A.8 B.12 C.16 D.18
6、如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )
A.12 B.14 C.16 D.18
7、如图,在△ABC中,∠BAC=90°,AD是BC边上的高,BE是AC边的中线,CF是∠ACB的角平分线,CF交AD于点G,交BE于点H,下面说法正确的有( )个①△ABE的面积=△BCE的面积;②∠FAG=∠FCB;③AF=AG;④BH=CH.
A.1 B.2 C.3 D.4
8、如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为 .如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是 .
9、如图,中,BE为AC边上的高,CD平分,CD、BE相交于点F.若,,求的度数.
10、如图,△ABC中,AD是高,AE、BF是角平分线,它们相交于点O,∠CAB=50°,∠BOA=120°,求∠DAE和∠C的度数.
11、如图,在△ABC中,AB>AC,AD是中线,将三角形的周长分为15cm和12cm两部分AB+AC=21,求AB、AC的长.
12、如图,在 中, , 边上的高 , 为 边上任一点, 于点 , 于点 ,求 的值.
挑战题:
1、如图,将三角形纸片ABC沿DE折叠,使B与C重合,CD,AE相交于F,已知BD=4AD,设△ABC的面积为S,△CEF的面积为S1,△ADF的面积为S2,则 的值为( )
A. B. C. D.
考点三、三角形的稳定性
知识点:
1. 三角形具有稳定性。
2. 四边形及多边形不具有稳定性。
相应练习:
1、人字梯中间一般会设计一“拉杆”,这样做的道理是( )
A.两点之间线段最短 B.三角形的稳定性
C.两点确定一条直线 D.垂线段最短
2、如图,工人师傅做了一个长方形窗框 分别是四条边上的中点,为使它稳固,需要在窗框上钉一根木条,这根木条不能钉在( )
A. 两点之间 B. 两点之间
C. 两点之间 D. 两点之间
3、小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理.
答案解析:
考点一、三角形三边的关系
1、【答案】D
【解析】【解答】解: 三角形的三边长分别为2,,5,
由①得:
由②得:
所以:
所以x的取值范围是
故答案为:D.
【分析】三角形两边之和大于第三边,两边之差小于第三边,列出不等式组,据此解答即可.
2、【答案】3
【解析】【解答】解:设腰长为x,则底边为7-2x.
∵7-2x-x<x<7-2x+x,
∴1.75<x<3.5,
∵三边长均为整数,
∴x可取的值为2或3,
故各边的长为2,2,3或3,3,1.
∴该三角形最长边的长为3cm.
故答案为:3.
【分析】设腰长为x,则底边为7-2x,根据三角形的三边关系可得x的范围,结合x为整数可得x的值,进而得到三角形的三边长,据此可得最长边的长.
3、【答案】(1)解:∵,
∴,,
∴,,
第三边长为c,求c的取值范围是:,
即.
(2)解:由(1)得,,,
是等腰三角形,当a为腰时,的周长为:9+9+4=22,
当b为腰时,4+4<9,不能构成三角形,舍去.
【解析】【分析】(1)根据二次根式及偶次幂的非负性,由两个非负数的和为0,则每一个数都等于0,求出a、b的值,再利用三角形的三边关系求出C的范围即可;
(2) 分两种情况:当a为腰、b为底或当b为腰、a为底,据此分别求解即可.
4、【答案】(1)解:根据三角形的三边关系,
,
解得:3<m<5;
(2)解:因为△ABC的三边均为整数,且3<m<5,所以m=4.
所以,△ABC 的周长为:(m 2)+(2m+1)+8=3m+7=3×4+7=19.
【解析】【分析】(1)根据三角形三边的关系可得,再求出m的取值范围即可;
(2)根据m的值为整数可得m的值,再利用三角形的周长公式计算即可。
5、【答案】解:∵b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,
∴|b+c-a|+|b-c-a|+|c-a-b|-|a-b+c|
=(b+c-a)-(b-c-a)-(c-a-b)-(a-b+c)
=(b+c-a-b+c+a-c+a+b-a+b-c
=2b
【解析】【分析】根据三角形的任意两边之和大于第三边,任意两边之差小于第三边及不等式的性质得出 b+c-a>0,b-c-a<0.c-a-b<0,a-b+c>0,再根据绝对值的意义去掉绝对值的符号,合并同类项即可.
挑战题:
【答案】5
【解析】【解答】解:因为不等边△ABC的两条高的长度分别为4和12,根据面积相等可设 △ABC的两边长为3x,x;
因为 3x×4=12×x(2倍的面积),面积S=6x,
因为知道两条边的假设长度,根据两边之和大于第三边,两边之差小于第三边可得:2x<第三边长度<4x,
因为要求高的最大长度,所以当第三边最短时,在第三边上的高就越长,
S=×第三边的长×高,6x>×2x×高,6x<×4x×高,
∴6>高>3,
∵是不等边三角形,且高为整数,
∴高的最大值为5,
故答案为:5.
【分析】根据 不等边△ABC的两条高的长度分别为4和12, 求解即可。
考点二、三角形的高、中线与角平分线
1、【答案】C
【解析】【解答】解:A、在△ABC中, AD是BC边上的高,该说法正确,故本选项不符合题意;
B、在△GBC 中,CF是BG边上的高,该说法正确,故本选项不符合题意;
C、在△ABC 中,GC不是BC边上的高,该说法错误,故本选项符合题意;
D、在△GBC 中,GC 是BC边上的高,该说法正确,故本选项不符合题意.
故答案为:C.
【分析】过三角形一个顶点向其对边所在的直线引垂线,顶点与垂足间的线段就是三角形的高,利用三角形高线的定义,对各选项逐一判断即可.
2、【答案】D
【解析】【解答】解:A、B、C均不是高线.
故答案为:D.
【分析】利用作高的方法对每个选项一一判断即可。
3、【答案】A
【解析】【解答】解:∵线段AP是BC边上在的高线,
∴根据垂线段最短得:PA≤AQ,PA≤AR.
故答案为:A.
【分析】根据等腰三角形的性质可得底边的高线、中线和角平分线重合,然后结合垂线段最短的性质进行判断.
4、【答案】C
【解析】【解答】解:∵△PDE是△CDE沿DE折叠而来,
∴CD=DP,
∵点D为AC的中点,AC=6
∴CD=DP=AD=3,
∵点P为AB的中点,AB=8,
∴AP= =4,
∴△ADP的周长=AD+DP+AP=3+3+4=10.
故答案为:C.
【分析】根据折叠的性质可得CD=DP,再利用中点的性质可得CD=DP=AD=3,AP= =4,最后利用三角形的周长公式计算即可。
5、【答案】C
【解析】【解答】解:∵F是EC的中点,
∴,
∴,
∵ E是BD的中点 ,
∴,,
∵,
∴,
∴,
故答案为:C.
【分析】根据三角形中线的性质可得,,,再结合,即可得到。
6、【答案】D
【解析】【解答】解:连接AE和CD,
∵BD=AB,
∴S△ABC=S△BCD=1,S△ACD=1+1=2,
∵AF=3AC,
∴FC=4AC,
∴S△FCD=4S△ACD=4×2=8,
同理可以求得:S△ACE=2S△ABC=2,则S△FCE=4S△ACE=4×2=8;
S△DCE=2S△BCD=2×1=2;
∴S△DEF=S△FCD+S△FCE+S△DCE=8+8+2=18.
故答案为:D.
【分析】连接AE和CD, 根据同高三角形的面积之间的关系可得S△ABC=S△BCD=1,S△ACD=2,S△FCD=4S△ACD=8,同理可得:S△ACE=2S△ABC,则S△FCE=4S△ACE,S△DCE=2S△BCD,然后根据S△DEF=S△FCD+S△FCE+S△DCE进行计算.
7、【答案】B
【解析】【解答】解:∵BE是AC边的中线
∴AE=CE
∵∠BAC=90°
∴ ,
∴△ABE的面积=△BCE的面积
故①正确;
∵AD是BC边上的高
∴∠FAG+∠ABC=90°
∵∠BAC=90°
∴∠ABC+∠ACB=90°
∴∠FAG=∠ACB
∵CF是∠ACB的角平分线
∴∠FCB= ∠ACB=∠ACF
∴
故②错误;
∵∠AFG+∠ACF=∠DGC+∠FCB=90°,∠AGF=∠DGC
∴∠AFG=∠AGF
∴AF=AG
故③正确;
根据已知条件无法证明BH=CH
故④错误;
故答案为:B.
【分析】根据三角形中线的性质可得△ABE的面积=△BCE的面积,据此判断①;根据余角的性质可得∠FAG=∠ACB,由角平分线的定义可得∠FCB=∠ACB=∠ACF,即得,据此判断②;根据余角的性质可得∠AFG=∠AGF,可得AF=AG,据此判断③;根据已知条件无法证明BH=CH,据此判断④.
8、【答案】16;
【解析】【解答】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF= BC,EG= AC,FG= AB,
∴EF+FG+EG= (BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为 ×64=16,
以此类推,第n个小三角形的周长是第一个三角形周长的64×( )n-1,
故答案为:16,64×( )n-1.
【分析】根据三角形中位线定理求出△EFG的周长;然后找出规律,第n个小三角形的周长是第一个三角形周长的64×( )n-1。
9、【答案】解:在中,,,
,
平分,
,
为边上的高,
,
.
【解析】【分析】根据三角形的角平分线、中线和高,以及角的运算法则即可得出答案。
10、【答案】解:∵AE是角平分线,∠CAB=50°,
∴ ,
∵∠BOA=120°,
∴ ,
∵BF是角平分线,
∴ ,
∴ ;
∴ ,
∵AD是高,
∴ .
【解析】【分析】根据AE是角平分线,∠CAB=50°,求出 ,再根据∠BOA=120°,利用三角形内角和定理求出∠ABF的度数,再根据BF是角平分线,得出 ,再利用三角形的内角和定理可求出∠AEB的度数,即可求出∠EAD的度数,即可得出结论。
11、【答案】解:∵AD是△ABC的中线,
∴BD=CD,
∵△ABD的周长=AB+BD+AD,
△ACD的周长=AC+CD+AD =AC+BD+AD,
∴△ABD的周长-△ACD的周长=AB-AC=3.
又∵AB+AC=21,
即: ,
解方程组,得,AB=12,AC=9
答:AB和AC的长分别为12cm和9cm.
【解析】【分析】由中线的定义可得BD=CD, 由三角形的周长差可得AB-AC=3. 结合已知可得关于AB、AC的方程组,解方程组可求得AB、AC的长.
12、【答案】解:连接 ,
∵CD⊥AB, , ,
∴ , , ,
∵ ,
∴ ,
又∵ , ,
∴ .
【解析】【分析】连接AP,根据三角形面积的计算公式即可得到PM+PN的值。
挑战题:
【答案】C
【解析】【解答】解:由折叠可知 ,
∴ ,
∴ ,
∴①,
过E作EH⊥AB于H,CM垂直AB交BA的延长线于M,
∴ , ,
∵BD=4AD,
∴ ,
∴②,
①-②得: ,
∵CM⊥AB,
∴ ,
,
∴ ,
∴ ,
∴ ,
∴ ,
故答案为:C.
【分析】先求出 ,再求出 ,最后计算求解即可。
考点三、三角形的稳定性
1、【答案】B
【知识点】三角形的稳定性
【解析】【解答】解:人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加梯子的稳定性.
故答案为:B.
【分析】三角形具有稳定性,据此解答即可.
2、【答案】D
【知识点】三角形的稳定性
【解析】【解答】解:A.若钉在E,H两点之间构成了三角形,能固定窗框,故不符合题意;
B.若钉在A,C两点之间能构成三角形,能固定窗框,故不符合题意;
C.若钉在F,E两点之间能构成三角形,能固定窗框,故不符合题意;
D.若钉在E,G两点之间不能构成三角形,不能固定窗框,故符合题意;
故答案为:D.
【分析】利用三角形的定义判断求解即可。
3、【答案】解:如图所示:
【知识点】三角形的稳定性
【解析】【分析】 根据三角形具有稳定性,主要是应用了三角形的稳定性.
