2021-2022学年苏科版九年级数学下册 5.2 二次函数的图像和性质 一课一练 (Word版含答案)
文档属性
| 名称 | 2021-2022学年苏科版九年级数学下册 5.2 二次函数的图像和性质 一课一练 (Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-07 11:37:09 | ||
图片预览



文档简介
5.2 二次函数的图像和性质(5)
1.二次函数的图象的对称轴是( )
A. B. C. D.
2.已知二次函数,且,则图象一定经过( )象限.
A.三、四 B.一、三、四 C.一、二、三、四 D.二、三、四
3.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为 ②抛物线与y轴的交点为
③抛物线的对称轴是:直线 ④在对称轴左侧y随x的增大而增大
A.1 B.2 C.3 D.4
4.对于二次函数,下列结果中正确的是( ).
A.抛物线有最小值是 B.时随的增大而减小
C.抛物线的对称轴是直线 D.图象与轴没有交点
5.已知抛物线,点在该抛物线上,下列正确的是( )
A. B. C. D.
6.抛物线y=x2+2x+7的开口方向 ___,顶点坐标 ___.
7.(1)抛物线必过__________点.
(2)若二次函数经过原点,则__________,则它的解析式是__________.
(3)若二次函数的最大值是3,则__________.
8.对于二次函数,图象的对称轴为____________,当自变量x满足时,函数值y的取值范围为,则a的取值范围为________.
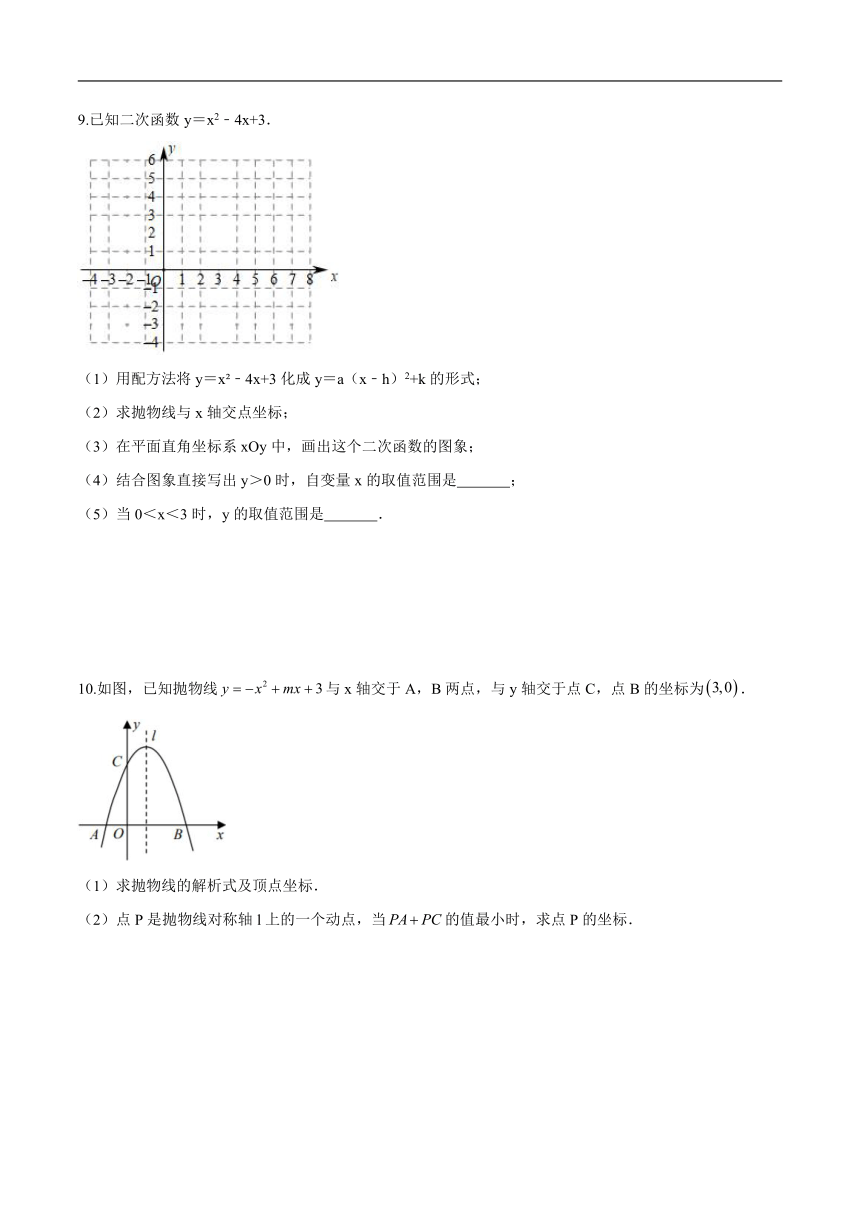
9.已知二次函数y=x2﹣4x+3.
(1)用配方法将y=x ﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求抛物线与x轴交点坐标;
(3)在平面直角坐标系xOy中,画出这个二次函数的图象;
(4)结合图象直接写出y>0时,自变量x的取值范围是 ;
(5)当0<x<3时,y的取值范围是 .
10.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为.
(1)求抛物线的解析式及顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当的值最小时,求点P的坐标.
11.将二次函数y=2x 2-8x-1化成y=a(x-h)2+k的形式,结果为( )
A.y=2(x-2)2-1 B.y=2(x-4)2+32
C.y=2(x-2)2-9 D.y=2(x-4)2-33
12.关于抛物线,下列说法错误的是( )
A.该抛物线经过原点 B.该抛物线的对称轴是直线
C.该抛物线的最大值为1 D.当时,随增大而减小
13.若抛物线y=x2-bx+8的顶点在x轴的负半轴上,则b=( )
A. B. C. D.
14.已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=2x2+8x+m上的点,则( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
15.(1)已知函数,当______时,y随x的增大而减小,当_______时,y随x的增大而增大;
(2)已知函数,当______时,y随x的增大而增大,当_______时,y随x的增大而减小.
16.二次函数y=x2—2x一2的图象向右平移2个单位长度后,再向上平移5个单位长度,平移后的图象对应的二次函数解析式为_______.
17.如图,已知⊙P的半径为1,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为__________________.
已知二次函数,当时,的取值范围为______.
19.已知二次函数.
(1)将其化成的形式;(2)写出开口方向,对称轴方程,顶点坐标;
(3)求图象与两坐标轴的交点坐标;(4)画出函数图象;
(5)说明其图象与抛物线的关系;(6)当x取何值时,y随x增大而减小;
(7)x取何值时,;(8)当x取何值时,函数y有最值?并求出最值?
(9)时,y的取值范围;(10)求函数图象与两坐标轴交点所围成的三角形面积.
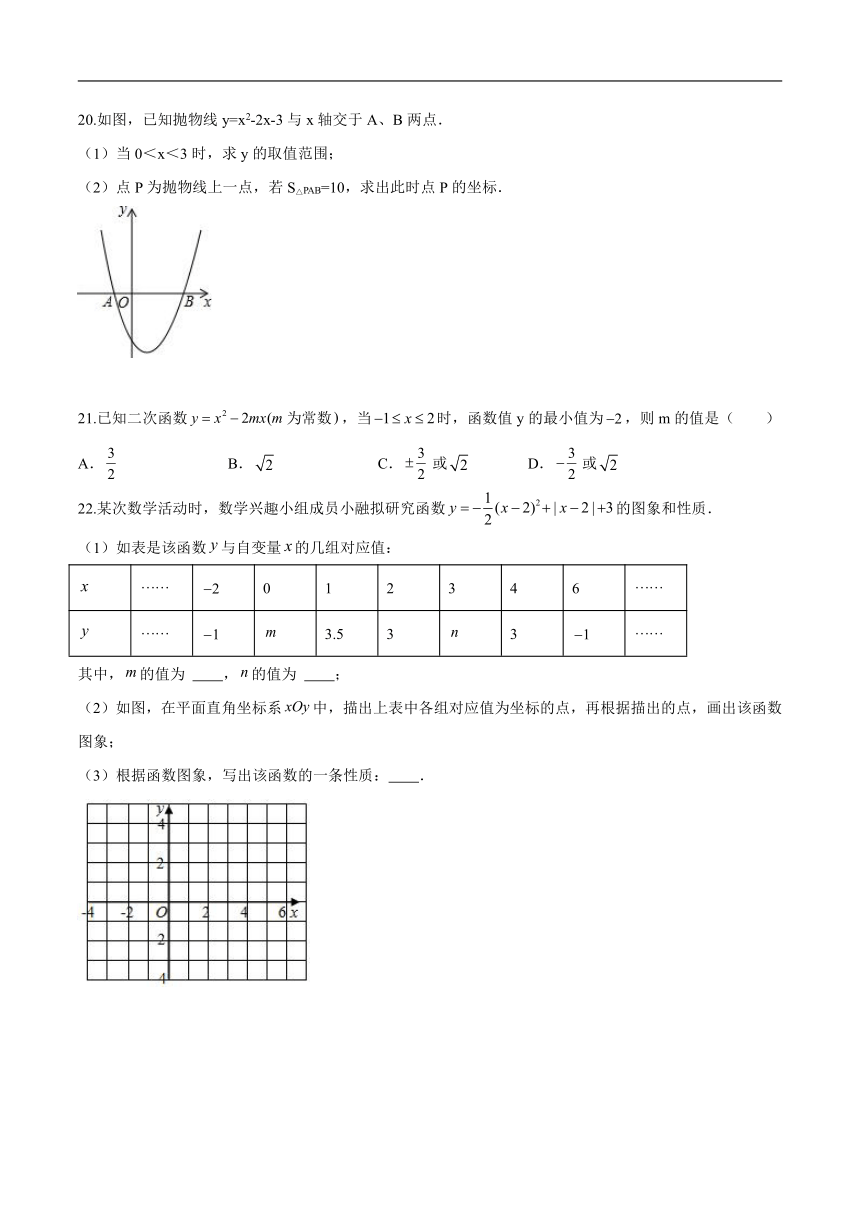
20.如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
21.已知二次函数为常数,当时,函数值y的最小值为,则m的值是( )
A. B. C.或 D.或
22.某次数学活动时,数学兴趣小组成员小融拟研究函数的图象和性质.
(1)如表是该函数与自变量的几组对应值:
0 1 2 3 4 6
3.5 3 3
其中,的值为 ,的值为 ;
(2)如图,在平面直角坐标系中,描出上表中各组对应值为坐标的点,再根据描出的点,画出该函数图象;
(3)根据函数图象,写出该函数的一条性质: .
5.2 二次函数的图像和性质(5)
1.二次函数的图象的对称轴是( )
A. B. C. D.
【答案】A
【解析】解:.
二次函数的图象的对称轴是.
故选A.
2.已知二次函数,且,则图象一定经过( )象限.
A.三、四 B.一、三、四 C.一、二、三、四 D.二、三、四
【答案】A
【解析】解:∵二次函数中,,,
∴二次函数的解析式为,二次函数的开口向下,二次函数与y轴的交点在y轴的负半轴,
∴二次函数的顶点坐标为(0,c),在y轴负半轴,
∴二次函数的图象 经过三、四象限;
故选A.
3.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为 ②抛物线与y轴的交点为
③抛物线的对称轴是:直线 ④在对称轴左侧y随x的增大而增大
A.1 B.2 C.3 D.4
【答案】C
【解析】解:根据表格中信息,得:
当 时, ,当时 , ,
∴点,在抛物线上,故①②正确;
根据表格中信息,得:
当 时, ,
当 时,,
∴抛物线的对称轴为 ,故③错误;
∵ ,
∴抛物线开口向下,
∴在对称轴左侧y随x的增大而增大,故④正确;
所以正确的有①②④,共3个.
故选:C.
4.对于二次函数,下列结果中正确的是( ).
A.抛物线有最小值是 B.时随的增大而减小
C.抛物线的对称轴是直线 D.图象与轴没有交点
【答案】A
【解析】解:∵=2(x+)2 ,
∴抛物线的对称轴为直线x= ,二次函数有最小值 ;所以A选项正确,C选项错误;
当x< 时,y随x的增大而减小,所以B选项错误;
∵方程2x2+x 3=0有两个不相等的实数解,
∴抛物线与x轴有两个交点,所以D选项错误.
故选:A.
5.已知抛物线,点在该抛物线上,下列正确的是( )
A. B. C. D.
【答案】A
【解析】解:∵抛物线,
∴抛物线开口向下,对称轴直线,
∵点在该抛物线上,
∴三点都在对称轴的右侧,y随x的增大而减小,
∵ 1<0<1,
∴,
故选:A.
6.抛物线y=x2+2x+7的开口方向 ___,顶点坐标 ___.
【答案】向上
【解析】解:原式,
则函数的开口方向向上,顶点坐标为,
故答案为:向上、.
7.(1)抛物线必过__________点.
(2)若二次函数经过原点,则__________,则它的解析式是__________.
(3)若二次函数的最大值是3,则__________.
【答案】(1)原点;(2);(3)
【解析】解:(1)
当时,则 抛物线必过原点.
(2) 二次函数经过原点,
则它的解析式是.
(3) 二次函数的最大值是3,
<且
经检验:它们都是原方程的根,但不合题意,舍去,
故答案为:(1)原点;(2);(3)
8.对于二次函数,图象的对称轴为____________,当自变量x满足时,函数值y的取值范围为,则a的取值范围为________.
【答案】直线
【解析】解:∵二次函数,
∴对称轴为直线;
∵,
∴当 时,函数有最小值,最小值为 ,
当 时,有,
解得: ,
∴如图所示,点A,B的坐标分别为,
∴当时, ,
∵时,函数值y的取值范围为,
从图象中可得到时,.
故答案为:直线;.
9.已知二次函数y=x2﹣4x+3.
(1)用配方法将y=x ﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求抛物线与x轴交点坐标;
(3)在平面直角坐标系xOy中,画出这个二次函数的图象;
(4)结合图象直接写出y>0时,自变量x的取值范围是 ;
(5)当0<x<3时,y的取值范围是 .
【答案】(1)y=(x﹣2)2﹣1;(2)该图象与x轴的交点坐标为(1,0)或(3,0);(3)画函数图象见解析;(4)或;(5)﹣1<y<3.
【解析】解:(1)y=x2﹣4x+3=(x﹣2)2﹣1;
(2)由二次函数y=x2﹣4x+3=(x﹣1)(x﹣3)知,
该图象与x轴的交点为(1,0)或(3,0);
(3)当x=0时,y=3;
当x=1时,y=0;
当x=﹣2时,y=﹣1;
当x=3时,y=0;
当x=4时,y=3,
用上述五点描点连线得到函数图象如下:
(4)观察函数图象知,当自变量x的取值范围满足或时,y>0.
故答案是:或;
(5)观察函数图象知,当0<x<3时,y的取值范围是:﹣1<y<3.
故答案是:﹣1<y<3.
10.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为.
(1)求抛物线的解析式及顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当的值最小时,求点P的坐标.
【答案】(1),;(2)点P的坐标为
【解析】解:(1)由题意得:,
解得:,
∴,
∴顶点坐标为:;
(2)连接BC交抛物线对称轴l于点P,则此时的值最小,
设直线BC的解析式为:,
由题意得:,
解得,
∴直线BC的解析式为:,
当时,,
∴当的值最小时,点P的坐标为.
11.将二次函数y=2x 2-8x-1化成y=a(x-h)2+k的形式,结果为( )
A.y=2(x-2)2-1 B.y=2(x-4)2+32
C.y=2(x-2)2-9 D.y=2(x-4)2-33
【答案】C
【解析】解:y=2x 2-8x-1
=2(x 2-4x+4)-8-1
=2(x-2)2-9,
即y=2(x-2)2-9.
故选C.
12.关于抛物线,下列说法错误的是( )
A.该抛物线经过原点 B.该抛物线的对称轴是直线
C.该抛物线的最大值为1 D.当时,随增大而减小
【答案】D
【解析】解:当抛物线,当时,,
经过原点,正确,
配方得:,
顶点坐标是,对称轴是直线,根据,得出开口向下有最大值,当时,随的增大而减小,、说法正确;
说法错误.
故选.
13.若抛物线y=x2-bx+8的顶点在x轴的负半轴上,则b=( )
A. B. C. D.
【答案】B
【解析】解:抛物线的顶点在轴的负半轴上,
顶点的横坐标小于0,纵坐标为零,即,,解得,
故选:B.
14.已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=2x2+8x+m上的点,则( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
【答案】D
【解析】解:抛物线的对称轴为直线,
∵,∴时,函数值最小,
又∵-1到-2的距离比-4到-2的距离小,∴∴.
故选D.
15.(1)已知函数,当______时,y随x的增大而减小,当_______时,y随x的增大而增大;
(2)已知函数,当______时,y随x的增大而增大,当_______时,y随x的增大而减小.
【答案】-1 -1
【解析】(1)∵,
∴抛物线开口向上,对称轴为直线,
∴当时,y随x的增大而减小;当时,y随x的增大而增大;
故答案为:
(2)∵,
∴抛物线开口向下,对称轴为直线,
∴当时,y随x的增大而增大;当时,y随x的增大而减小.
故答案为:
16.二次函数y=x2—2x一2的图象向右平移2个单位长度后,再向上平移5个单位长度,平移后的图象对应的二次函数解析式为_______.
【答案】y=(x-4)2+1
【解析】解:∵y=x2-2x-2=(x-2)2-4,
把其图象向右平移2个单位长度,再向上平移5个单位长度,
得抛物线y=(x-2-2)2-4+5,
即为y=(x-4)2+1.
故答案为:y=(x-4)2+1.
17.如图,已知⊙P的半径为1,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为__________________.
【答案】(2,1)或(﹣2,1)或(0,﹣1)
【解析】解:∵⊙P与x轴相切,∴P到x轴的距离等于半径1,∴点P的纵坐标为1或﹣1,
当y=1时,代入可得1=x2﹣1,解得x=2或x=﹣2,此时P点坐标为(2,1)或(﹣2,1);
当y=﹣1时,代入可得﹣1=x2﹣1,解得x=0,此时P点坐标为(0,﹣1);
综上可知P点坐标为(2,1)或(﹣2,1)或(0,﹣1),
故答案为:(2,1)或(﹣2,1)或(0,﹣1).
18.已知二次函数,当时,的取值范围为______.
【答案】
【解析】∵
∴抛物线的对称轴为直线x=-1,顶点坐标为(-1,4)
∵二次项系数1为正数
∴当-4≤x≤-1时,函数值y随自变量x的增大而减小;当-1≤x≤1时,函数值y随自变量x的增大而增大,函数的最小值为-4
∵当x=-4时,y=5,当x=1时,y=0
∴当-4≤x≤-1时,-4≤y≤5;当-1≤x≤1时,-4≤y≤0
综上,当时,的取值范围为
故答案为:
19.已知二次函数.
(1)将其化成的形式;(2)写出开口方向,对称轴方程,顶点坐标;
(3)求图象与两坐标轴的交点坐标;(4)画出函数图象;
(5)说明其图象与抛物线的关系;(6)当x取何值时,y随x增大而减小;
(7)x取何值时,;(8)当x取何值时,函数y有最值?并求出最值?
(9)时,y的取值范围;(10)求函数图象与两坐标轴交点所围成的三角形面积.
【答案】(1);(2)开口向上,直线,顶点;(3)与x轴交点,与y轴交点;(4)见解析;(5)将抛物线向左平移1个单位,向下平移8个单位;得到的图象;(6);(7)当或时,;当或时,;当时,;(8)时,;(9);(10).
【解析】解:(1)∵===
∴化成的形式为;
(2)由可得:
开口向上,对称轴为直线x=-1,顶点坐标为(-1,-8);
(3)由y=0得,,解得或,
由x=0得:∴与x轴交点坐标为(-3,0),(1,0),与y轴交点坐标为(0,-6);
(4)由(1)(2)(3)可得函数简图如下:
(5)将抛物线先向左平移1个单位,可得的图象,然后再向下平移8个单位得到的图像;
(6)由图像可得:当时,y随x增大而减小;
(7)由图像可得:当或时,,
当或时,,
当时,;
(8)由图像可得:
当时,函数有最小值,且最小值为;
(9)∵,∴当时取得最小值为,
当时离对称轴最远,此时,∴y的取值范围为;
(10)由图可得,三角形底的长度为,高的长度为6,
∴三角形的面积为.
20.如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
【答案】(1) ﹣4≤y<0;(2) P点坐标为(﹣2,5)或(4,5)
【解析】 解:(1)∵抛物线的解析式为y=x2﹣2x﹣3,∴y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4),由图可得当0<x<3时,﹣4≤y<0.
(2)当y=0时,x2﹣2x﹣3=0, 解得:x1=-1 x2=3
∵A(﹣1,0)、B(3,0), ∴AB=4.
设P(x,y),则S△PAB=AB |y|=2|y|=10, ∴|y|=5, ∴y=±5.
①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,
此时P点坐标为(﹣2,5)或(4,5);
②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;
综上所述,P点坐标为(﹣2,5)或(4,5).
21.已知二次函数为常数,当时,函数值y的最小值为,则m的值是( )
A. B. C.或 D.或
【答案】D
【解析】解:∵二次函数(为常数),
∴抛物线的对称轴为直线x==m,
当m<-1时,-1<x<2表示的数在对称轴的右侧,
∵二次函数(为常数)中,a=1>0,
∴在对称轴的右侧,y随x的增大而增大,
∴当x=-1时,函数y取得最小值,即1+2m=-2,解得m=;
当-1<m<2时,
∵二次函数(为常数)中,a=1>0,函数有最小值,
∴当x=m时,y取得最小值,即=-2,
解得m= 或m=-(不在范围内,舍去);
当m>2时,
∵二次函数(为常数)中,a=1>0,
∴在对称轴的左侧,y随x的增大而减小,
∴当x=2时,函数y取得最小值,即4-4m=-2,解得m=,(不在范围内,舍去)
综上所述,m的值为或,
故选D.
22.某次数学活动时,数学兴趣小组成员小融拟研究函数的图象和性质.
(1)如表是该函数与自变量的几组对应值:
0 1 2 3 4 6
3.5 3 3
其中,的值为 ,的值为 ;
(2)如图,在平面直角坐标系中,描出上表中各组对应值为坐标的点,再根据描出的点,画出该函数图象;
(3)根据函数图象,写出该函数的一条性质: .
【答案】(1)3,3.5;(2)见解析;(3)图象关于直线对称.
【解析】解(1)当时,,即,
当时,,即
故答案为:3,3.5;
(2)图象如图所示:
(3)观察图象可知,图象关于直线对称,
故答案为:图象关于直线对称.
1.二次函数的图象的对称轴是( )
A. B. C. D.
2.已知二次函数,且,则图象一定经过( )象限.
A.三、四 B.一、三、四 C.一、二、三、四 D.二、三、四
3.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为 ②抛物线与y轴的交点为
③抛物线的对称轴是:直线 ④在对称轴左侧y随x的增大而增大
A.1 B.2 C.3 D.4
4.对于二次函数,下列结果中正确的是( ).
A.抛物线有最小值是 B.时随的增大而减小
C.抛物线的对称轴是直线 D.图象与轴没有交点
5.已知抛物线,点在该抛物线上,下列正确的是( )
A. B. C. D.
6.抛物线y=x2+2x+7的开口方向 ___,顶点坐标 ___.
7.(1)抛物线必过__________点.
(2)若二次函数经过原点,则__________,则它的解析式是__________.
(3)若二次函数的最大值是3,则__________.
8.对于二次函数,图象的对称轴为____________,当自变量x满足时,函数值y的取值范围为,则a的取值范围为________.
9.已知二次函数y=x2﹣4x+3.
(1)用配方法将y=x ﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求抛物线与x轴交点坐标;
(3)在平面直角坐标系xOy中,画出这个二次函数的图象;
(4)结合图象直接写出y>0时,自变量x的取值范围是 ;
(5)当0<x<3时,y的取值范围是 .
10.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为.
(1)求抛物线的解析式及顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当的值最小时,求点P的坐标.
11.将二次函数y=2x 2-8x-1化成y=a(x-h)2+k的形式,结果为( )
A.y=2(x-2)2-1 B.y=2(x-4)2+32
C.y=2(x-2)2-9 D.y=2(x-4)2-33
12.关于抛物线,下列说法错误的是( )
A.该抛物线经过原点 B.该抛物线的对称轴是直线
C.该抛物线的最大值为1 D.当时,随增大而减小
13.若抛物线y=x2-bx+8的顶点在x轴的负半轴上,则b=( )
A. B. C. D.
14.已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=2x2+8x+m上的点,则( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
15.(1)已知函数,当______时,y随x的增大而减小,当_______时,y随x的增大而增大;
(2)已知函数,当______时,y随x的增大而增大,当_______时,y随x的增大而减小.
16.二次函数y=x2—2x一2的图象向右平移2个单位长度后,再向上平移5个单位长度,平移后的图象对应的二次函数解析式为_______.
17.如图,已知⊙P的半径为1,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为__________________.
已知二次函数,当时,的取值范围为______.
19.已知二次函数.
(1)将其化成的形式;(2)写出开口方向,对称轴方程,顶点坐标;
(3)求图象与两坐标轴的交点坐标;(4)画出函数图象;
(5)说明其图象与抛物线的关系;(6)当x取何值时,y随x增大而减小;
(7)x取何值时,;(8)当x取何值时,函数y有最值?并求出最值?
(9)时,y的取值范围;(10)求函数图象与两坐标轴交点所围成的三角形面积.
20.如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
21.已知二次函数为常数,当时,函数值y的最小值为,则m的值是( )
A. B. C.或 D.或
22.某次数学活动时,数学兴趣小组成员小融拟研究函数的图象和性质.
(1)如表是该函数与自变量的几组对应值:
0 1 2 3 4 6
3.5 3 3
其中,的值为 ,的值为 ;
(2)如图,在平面直角坐标系中,描出上表中各组对应值为坐标的点,再根据描出的点,画出该函数图象;
(3)根据函数图象,写出该函数的一条性质: .
5.2 二次函数的图像和性质(5)
1.二次函数的图象的对称轴是( )
A. B. C. D.
【答案】A
【解析】解:.
二次函数的图象的对称轴是.
故选A.
2.已知二次函数,且,则图象一定经过( )象限.
A.三、四 B.一、三、四 C.一、二、三、四 D.二、三、四
【答案】A
【解析】解:∵二次函数中,,,
∴二次函数的解析式为,二次函数的开口向下,二次函数与y轴的交点在y轴的负半轴,
∴二次函数的顶点坐标为(0,c),在y轴负半轴,
∴二次函数的图象 经过三、四象限;
故选A.
3.抛物线上部分点的横坐标x,纵坐标y的对应值如下表:
x … 0 1 2 …
y … 0 4 6 6 4 …
从上表可知,下列说法正确的个数是( )
①抛物线与x轴的一个交点为 ②抛物线与y轴的交点为
③抛物线的对称轴是:直线 ④在对称轴左侧y随x的增大而增大
A.1 B.2 C.3 D.4
【答案】C
【解析】解:根据表格中信息,得:
当 时, ,当时 , ,
∴点,在抛物线上,故①②正确;
根据表格中信息,得:
当 时, ,
当 时,,
∴抛物线的对称轴为 ,故③错误;
∵ ,
∴抛物线开口向下,
∴在对称轴左侧y随x的增大而增大,故④正确;
所以正确的有①②④,共3个.
故选:C.
4.对于二次函数,下列结果中正确的是( ).
A.抛物线有最小值是 B.时随的增大而减小
C.抛物线的对称轴是直线 D.图象与轴没有交点
【答案】A
【解析】解:∵=2(x+)2 ,
∴抛物线的对称轴为直线x= ,二次函数有最小值 ;所以A选项正确,C选项错误;
当x< 时,y随x的增大而减小,所以B选项错误;
∵方程2x2+x 3=0有两个不相等的实数解,
∴抛物线与x轴有两个交点,所以D选项错误.
故选:A.
5.已知抛物线,点在该抛物线上,下列正确的是( )
A. B. C. D.
【答案】A
【解析】解:∵抛物线,
∴抛物线开口向下,对称轴直线,
∵点在该抛物线上,
∴三点都在对称轴的右侧,y随x的增大而减小,
∵ 1<0<1,
∴,
故选:A.
6.抛物线y=x2+2x+7的开口方向 ___,顶点坐标 ___.
【答案】向上
【解析】解:原式,
则函数的开口方向向上,顶点坐标为,
故答案为:向上、.
7.(1)抛物线必过__________点.
(2)若二次函数经过原点,则__________,则它的解析式是__________.
(3)若二次函数的最大值是3,则__________.
【答案】(1)原点;(2);(3)
【解析】解:(1)
当时,则 抛物线必过原点.
(2) 二次函数经过原点,
则它的解析式是.
(3) 二次函数的最大值是3,
<且
经检验:它们都是原方程的根,但不合题意,舍去,
故答案为:(1)原点;(2);(3)
8.对于二次函数,图象的对称轴为____________,当自变量x满足时,函数值y的取值范围为,则a的取值范围为________.
【答案】直线
【解析】解:∵二次函数,
∴对称轴为直线;
∵,
∴当 时,函数有最小值,最小值为 ,
当 时,有,
解得: ,
∴如图所示,点A,B的坐标分别为,
∴当时, ,
∵时,函数值y的取值范围为,
从图象中可得到时,.
故答案为:直线;.
9.已知二次函数y=x2﹣4x+3.
(1)用配方法将y=x ﹣4x+3化成y=a(x﹣h)2+k的形式;
(2)求抛物线与x轴交点坐标;
(3)在平面直角坐标系xOy中,画出这个二次函数的图象;
(4)结合图象直接写出y>0时,自变量x的取值范围是 ;
(5)当0<x<3时,y的取值范围是 .
【答案】(1)y=(x﹣2)2﹣1;(2)该图象与x轴的交点坐标为(1,0)或(3,0);(3)画函数图象见解析;(4)或;(5)﹣1<y<3.
【解析】解:(1)y=x2﹣4x+3=(x﹣2)2﹣1;
(2)由二次函数y=x2﹣4x+3=(x﹣1)(x﹣3)知,
该图象与x轴的交点为(1,0)或(3,0);
(3)当x=0时,y=3;
当x=1时,y=0;
当x=﹣2时,y=﹣1;
当x=3时,y=0;
当x=4时,y=3,
用上述五点描点连线得到函数图象如下:
(4)观察函数图象知,当自变量x的取值范围满足或时,y>0.
故答案是:或;
(5)观察函数图象知,当0<x<3时,y的取值范围是:﹣1<y<3.
故答案是:﹣1<y<3.
10.如图,已知抛物线与x轴交于A,B两点,与y轴交于点C,点B的坐标为.
(1)求抛物线的解析式及顶点坐标.
(2)点P是抛物线对称轴l上的一个动点,当的值最小时,求点P的坐标.
【答案】(1),;(2)点P的坐标为
【解析】解:(1)由题意得:,
解得:,
∴,
∴顶点坐标为:;
(2)连接BC交抛物线对称轴l于点P,则此时的值最小,
设直线BC的解析式为:,
由题意得:,
解得,
∴直线BC的解析式为:,
当时,,
∴当的值最小时,点P的坐标为.
11.将二次函数y=2x 2-8x-1化成y=a(x-h)2+k的形式,结果为( )
A.y=2(x-2)2-1 B.y=2(x-4)2+32
C.y=2(x-2)2-9 D.y=2(x-4)2-33
【答案】C
【解析】解:y=2x 2-8x-1
=2(x 2-4x+4)-8-1
=2(x-2)2-9,
即y=2(x-2)2-9.
故选C.
12.关于抛物线,下列说法错误的是( )
A.该抛物线经过原点 B.该抛物线的对称轴是直线
C.该抛物线的最大值为1 D.当时,随增大而减小
【答案】D
【解析】解:当抛物线,当时,,
经过原点,正确,
配方得:,
顶点坐标是,对称轴是直线,根据,得出开口向下有最大值,当时,随的增大而减小,、说法正确;
说法错误.
故选.
13.若抛物线y=x2-bx+8的顶点在x轴的负半轴上,则b=( )
A. B. C. D.
【答案】B
【解析】解:抛物线的顶点在轴的负半轴上,
顶点的横坐标小于0,纵坐标为零,即,,解得,
故选:B.
14.已知(﹣1,y1),(﹣2,y2),(﹣4,y3)是抛物线y=2x2+8x+m上的点,则( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
【答案】D
【解析】解:抛物线的对称轴为直线,
∵,∴时,函数值最小,
又∵-1到-2的距离比-4到-2的距离小,∴∴.
故选D.
15.(1)已知函数,当______时,y随x的增大而减小,当_______时,y随x的增大而增大;
(2)已知函数,当______时,y随x的增大而增大,当_______时,y随x的增大而减小.
【答案】-1 -1
【解析】(1)∵,
∴抛物线开口向上,对称轴为直线,
∴当时,y随x的增大而减小;当时,y随x的增大而增大;
故答案为:
(2)∵,
∴抛物线开口向下,对称轴为直线,
∴当时,y随x的增大而增大;当时,y随x的增大而减小.
故答案为:
16.二次函数y=x2—2x一2的图象向右平移2个单位长度后,再向上平移5个单位长度,平移后的图象对应的二次函数解析式为_______.
【答案】y=(x-4)2+1
【解析】解:∵y=x2-2x-2=(x-2)2-4,
把其图象向右平移2个单位长度,再向上平移5个单位长度,
得抛物线y=(x-2-2)2-4+5,
即为y=(x-4)2+1.
故答案为:y=(x-4)2+1.
17.如图,已知⊙P的半径为1,圆心P在抛物线y=x2﹣1上运动,当⊙P与x轴相切时,圆心P的坐标为__________________.
【答案】(2,1)或(﹣2,1)或(0,﹣1)
【解析】解:∵⊙P与x轴相切,∴P到x轴的距离等于半径1,∴点P的纵坐标为1或﹣1,
当y=1时,代入可得1=x2﹣1,解得x=2或x=﹣2,此时P点坐标为(2,1)或(﹣2,1);
当y=﹣1时,代入可得﹣1=x2﹣1,解得x=0,此时P点坐标为(0,﹣1);
综上可知P点坐标为(2,1)或(﹣2,1)或(0,﹣1),
故答案为:(2,1)或(﹣2,1)或(0,﹣1).
18.已知二次函数,当时,的取值范围为______.
【答案】
【解析】∵
∴抛物线的对称轴为直线x=-1,顶点坐标为(-1,4)
∵二次项系数1为正数
∴当-4≤x≤-1时,函数值y随自变量x的增大而减小;当-1≤x≤1时,函数值y随自变量x的增大而增大,函数的最小值为-4
∵当x=-4时,y=5,当x=1时,y=0
∴当-4≤x≤-1时,-4≤y≤5;当-1≤x≤1时,-4≤y≤0
综上,当时,的取值范围为
故答案为:
19.已知二次函数.
(1)将其化成的形式;(2)写出开口方向,对称轴方程,顶点坐标;
(3)求图象与两坐标轴的交点坐标;(4)画出函数图象;
(5)说明其图象与抛物线的关系;(6)当x取何值时,y随x增大而减小;
(7)x取何值时,;(8)当x取何值时,函数y有最值?并求出最值?
(9)时,y的取值范围;(10)求函数图象与两坐标轴交点所围成的三角形面积.
【答案】(1);(2)开口向上,直线,顶点;(3)与x轴交点,与y轴交点;(4)见解析;(5)将抛物线向左平移1个单位,向下平移8个单位;得到的图象;(6);(7)当或时,;当或时,;当时,;(8)时,;(9);(10).
【解析】解:(1)∵===
∴化成的形式为;
(2)由可得:
开口向上,对称轴为直线x=-1,顶点坐标为(-1,-8);
(3)由y=0得,,解得或,
由x=0得:∴与x轴交点坐标为(-3,0),(1,0),与y轴交点坐标为(0,-6);
(4)由(1)(2)(3)可得函数简图如下:
(5)将抛物线先向左平移1个单位,可得的图象,然后再向下平移8个单位得到的图像;
(6)由图像可得:当时,y随x增大而减小;
(7)由图像可得:当或时,,
当或时,,
当时,;
(8)由图像可得:
当时,函数有最小值,且最小值为;
(9)∵,∴当时取得最小值为,
当时离对称轴最远,此时,∴y的取值范围为;
(10)由图可得,三角形底的长度为,高的长度为6,
∴三角形的面积为.
20.如图,已知抛物线y=x2-2x-3与x轴交于A、B两点.
(1)当0<x<3时,求y的取值范围;
(2)点P为抛物线上一点,若S△PAB=10,求出此时点P的坐标.
【答案】(1) ﹣4≤y<0;(2) P点坐标为(﹣2,5)或(4,5)
【解析】 解:(1)∵抛物线的解析式为y=x2﹣2x﹣3,∴y=x2﹣2x﹣3=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4),由图可得当0<x<3时,﹣4≤y<0.
(2)当y=0时,x2﹣2x﹣3=0, 解得:x1=-1 x2=3
∵A(﹣1,0)、B(3,0), ∴AB=4.
设P(x,y),则S△PAB=AB |y|=2|y|=10, ∴|y|=5, ∴y=±5.
①当y=5时,x2﹣2x﹣3=5,解得:x1=﹣2,x2=4,
此时P点坐标为(﹣2,5)或(4,5);
②当y=﹣5时,x2﹣2x﹣3=﹣5,方程无解;
综上所述,P点坐标为(﹣2,5)或(4,5).
21.已知二次函数为常数,当时,函数值y的最小值为,则m的值是( )
A. B. C.或 D.或
【答案】D
【解析】解:∵二次函数(为常数),
∴抛物线的对称轴为直线x==m,
当m<-1时,-1<x<2表示的数在对称轴的右侧,
∵二次函数(为常数)中,a=1>0,
∴在对称轴的右侧,y随x的增大而增大,
∴当x=-1时,函数y取得最小值,即1+2m=-2,解得m=;
当-1<m<2时,
∵二次函数(为常数)中,a=1>0,函数有最小值,
∴当x=m时,y取得最小值,即=-2,
解得m= 或m=-(不在范围内,舍去);
当m>2时,
∵二次函数(为常数)中,a=1>0,
∴在对称轴的左侧,y随x的增大而减小,
∴当x=2时,函数y取得最小值,即4-4m=-2,解得m=,(不在范围内,舍去)
综上所述,m的值为或,
故选D.
22.某次数学活动时,数学兴趣小组成员小融拟研究函数的图象和性质.
(1)如表是该函数与自变量的几组对应值:
0 1 2 3 4 6
3.5 3 3
其中,的值为 ,的值为 ;
(2)如图,在平面直角坐标系中,描出上表中各组对应值为坐标的点,再根据描出的点,画出该函数图象;
(3)根据函数图象,写出该函数的一条性质: .
【答案】(1)3,3.5;(2)见解析;(3)图象关于直线对称.
【解析】解(1)当时,,即,
当时,,即
故答案为:3,3.5;
(2)图象如图所示:
(3)观察图象可知,图象关于直线对称,
故答案为:图象关于直线对称.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
