中等解答题满分策略、综合性解答题破解对策(下)[上下学期通用]
文档属性
| 名称 | 中等解答题满分策略、综合性解答题破解对策(下)[上下学期通用] |

|
|
| 格式 | rar | ||
| 文件大小 | 755.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-12-20 00:00:00 | ||
图片预览








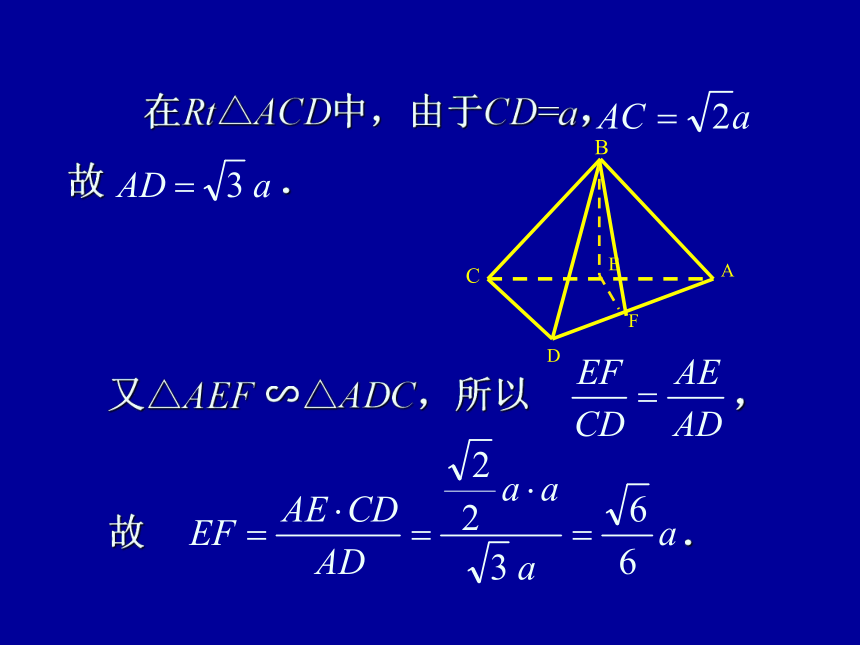

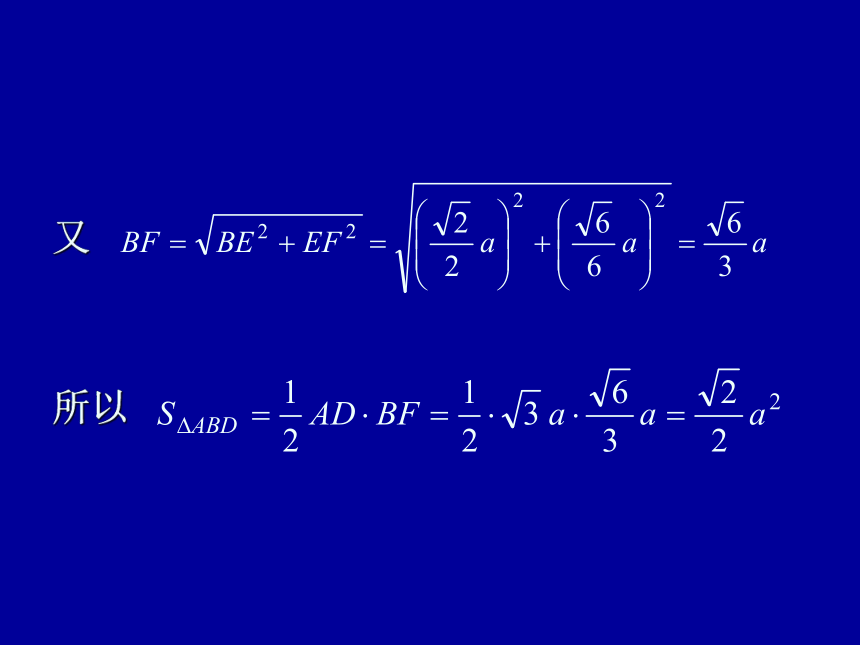
文档简介
课件58张PPT。清华同方“3+X”高分宝典数学(下)主讲:北京陈经纶中学 丁益祥(特级)
北 航 附 中 王人伟(特级)
例4 已知向量 所表示的复数z满足 ,
将 绕原点O按顺时针方向旋转
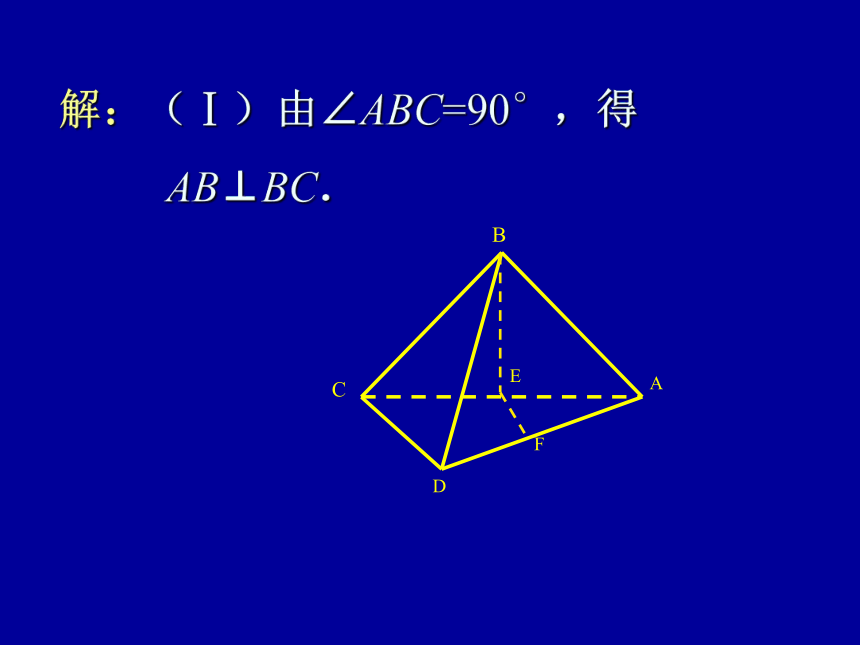
得 ,设 所表示的复数为z′,求复数 的辐角主值.解:由 ,得 . 于是 . 例5 如图,在平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使二面角
B-AC-D成直二面角.
(Ⅰ)求证:AB⊥面BCD;
(Ⅱ)求二面角B—AD—C
的大小;
(Ⅲ)求点C到平面ABD的
距离. 解:(Ⅰ)由∠ABC=90°,得
AB⊥BC.由于AB=BC=a,
故∠BCA=45°. 又在平面图形中,∠C=135°,
故在三棱锥中,∠ACD=90°.
从而CD⊥AC. 又因为二面角B-AC-D是直二面角,
所以 面ABC⊥面ACD,于是CD⊥面ABC,
因此 CD⊥AB .
故 AB⊥面BCD. (Ⅱ)过点B 作BE⊥AC于E,则BE = AE = CE,BE⊥面ACD. 过E 作EF⊥AD于F,连BF,由三垂线定理,知BF⊥AD.因此∠BFE是
二面角B—AD—C的平面角. 在Rt△ABC 中,由于AB=BC=a ,故. 在Rt△ACD中,由于CD=a,
故 . 又△AEF ∽△ADC,所以 ,
故 . 在Rt△BEF中, ,
故∠BFE=60°.
即二面角B-AD-C为60°. (Ⅲ)易知
.
又
所以 由于
设C到平面ABD的距离为d
则
即
解得
即点C到平面ABD的距离是 . 例6 某海军基地的三艘舰艇在某海域的A、B、C三处定点执行任务.已知A在B的正东方向,且A、B相距6千米.C在B的北偏西30°,B、C相距4千米.某时刻A处舰艇收到该海域内P处一渔船以每秒1千米的传播速度发出的“由于机器故障无法航行急需救助”的信号,4秒钟后B、C两处的舰艇才同时收到这一信号.现A处舰艇奉命前去救助,求A处舰艇前去救助时航向的方位角. 例6 某海军基地的三艘舰艇在某海域的A、B、C三处定点执行任务.已知A在B的正东方向,且A、B相距6千米.C在B的北偏西30°,B、C相距4千米.某时刻A处舰艇收到该海域内P处一渔船以每秒1千米的传播速度发出的“由于机器故障无法航行急需救助”的信号,4秒钟后B、C两处的舰艇才同时收到这一信号.现A处舰艇奉命前去救助,求A处舰艇前去救助时航向的方位角. 解:以BA所在直线为x轴,线段BA的中点为原点,正东、正北方向分别为x轴、y轴的正方向建立直角坐标系(如图), 则A(3,0),B(-3,0), =4. 过C作CM⊥x轴于M,由于C在B的北偏西 30°,故∠CBM = 60°. ∴ ,
,
于是得 .
由于B处舰艇收到信号比A处舰艇收到信号迟4秒,且信号传播速度为每秒1千米,
故|PB|-|PA|= 4. 因此,P点在以A、B为焦点的双曲
线的右支上,且 2a = 4,2c = 6,从而
a = 2,c = 3,b2 = c2-a2 = 5.
所以,双曲线的方程为
① 因为B、C两处舰艇同时收到P处渔船发出的呼救信号,所以|PB|=|PC|,于是点P必在线段BC 的垂直平分线上. 由点斜式得直线PQ 的方程为
整理,得 . ② 过P作PQ⊥BC于Q,则Q必为BC的中
点.故得 ,
.
联立①、②,注意到x≥2,解得x = 8,
,于是得 .
设PA的倾斜角为?,则
.
故 .因此所求的方位角为30°. 解好解答题中综合性难题的对策 一、“翻译”转化,弄清已知,明确
目标,理顺思路.
二、辨别题型,设计方案,寻求最
佳解法.
三、解前估测猜想,解后检验思考,
总结经验教训,分析错误原因.
例1.已知函数,f (x)=ax2-1 (a∈R,x∈R),集合
且A=B≠?.求a的取值范围.
抛物线y= ax2-1 与直线y=x的交点的横坐标. 方程ax2-1 =x的实根 方程a (ax2-1)2-1=x的实根 方程组 的解中x的值 曲线y=ax2-1与曲线x=ay2-1的公共点的横坐标. A=B≠? 集合A、B中元素都相同且不是空集 方程ax2-1=x有实根,且与方程
a (ax2-1)2-1=x同解 曲线y= ax2-1与y =x有交点,且
交点就是曲线y= ax2-1与x= ay2-1的交点. 由A≠?,得到a的一个范围;
证明 ;解题方案一(3) 由于 ,说明四次方程
a (ax2-1)2-1- x=0
左边的四次式必能因式分解,分解 出一个二次式ax2-1-x 与另一个二次式的乘积;
利用A=B再得出a的另一个范围.
(1) A≠? y=ax2-1与y=x有公共点;解题方案二 (2) A=B 曲线y= ax2-1上不存在两个
不同点关于直线y=x对称. 曲线y= ax2-1上斜率为-1 的平
行弦中点轨迹与y = x 没有公共点.
解题方案二解:(1) 由A≠?,知
方程ax2-x-1=0有实根, 当a=0时,该方程有实根; 当a≠0时,由△1≥0,得
1+4a≥0,
即 (a≠0),
综上,得 .(2) f [f (x)]=x即
a (ax2-1)2-1-x=0
a3x4-2a2x2-x+a-1=0
(ax2-x-1)(a2x2+ax-a+1)=0.
A=B当且仅当方程
a2x2+ax-a+1=0 ②
无实根或方程②的实根都是方程
ax2-x-1=0 ① 的实根,
方程①与②的实根不都相同 . 当△2=a2-4a2(-a+1)<0,即
时方程②无实根;
当△2=0,即 时,方程②有
重根 ,恰是方程①的两根之一;
∴ 当且仅当 时A=B.
综上,
A=B≠?时a的取值范围是 . 练习题 1 函数y =ax2-2的图像上存在不同两点关于直线y =x对称,求a的取值范围.例2.已知无穷数列{an}的每一项都是正
整数,且 ,
an0).
(1) 证明:an ≤an+1 (n∈N);
(2) 是否存在自然数m,当n≥m时,
an恒为一个常数?分析: 假设存在自然数k, ,那
么 ,
于是 ,
,
……
∵ 数列各项都是自然数,
∴
设 ,则 ,这与已知矛盾. (2) 如果存在自然数n, ,
那么
又因为 ,
∴ ,
从而
如果对于任意自然数n,都有 ,
那么因为已知此数列每一项都是自然数,
所以 ,从而
设 M 的整数部分是t,则
,
这与数列每一项都小于M 是矛盾的.
综上可知,存在自然数m,当n≥m 时,
an恒为一常数. 已知无穷数列{an}的每一项都是正整数,且 (n∈N),集合P={(x,y)|x=n,y=an,n∈N}.
求证:集合P 中有无穷多个点在一直线上.
练习题 2例3.已知抛物线顶点在x轴上,以y轴为准线,点A(4,0)到此抛物线上动点 P的距离的最小值为2,求此抛物线的方程.解:设所求抛物线顶点为(a,0),那么方 程为y2=4a (x-a).
设抛物线上动点P的坐标为 (x,y),
解得,
∴ 抛物线方程为
或 代数解法所得结论与解前估测的结
果不符,孰对孰错?
,
当4-2a≥a 即 时,
,
得 ;
分 析当 ,则x=a时|PA|最小,
∴ 得a=2或a=6. 综上,所求抛物线方程为
,
y2 =8(x-2),y2=24(x-6). 是否存在同时满足下列条件的双曲
线,若存在,求出方程;若不存在,说
明理由:
(1) 渐近线方程为x+2y=0 及x-2y=0 ;
(2) 点A (5,0)到双曲线上动点P 的距离
最小值为 .练习题 3 例4.设二次函数f (x)=ax2+bx+c (a>0),方
程f (x)-x=0的两个根x1,x2满足
(1) 当x∈(0,x1)时,证明x 证明: .证明一:(1) 令 ,
因x1,x2是方程f (x)-x=0的根,
所以 .
当 时, ,
又a>0,故 ,
即x∵ ,
∴ ,
,
∴ ,
(2) 依题意, .
∵ x1,x2是方程ax2+(b-1)x+c=0的根,
∴ .
∵ ,
∴ . 证明二:
由(2)的结论证明(1)的 .
∵ x=x0是f (x)图像的对称轴,且a>0,
∴ f (x)在 上递增,在
上递减.
当 时,f (x) 当 时,,∵ , ,
∴ ,
∴ .
综上两种情况,当 时,
.
北 航 附 中 王人伟(特级)
例4 已知向量 所表示的复数z满足 ,
将 绕原点O按顺时针方向旋转
得 ,设 所表示的复数为z′,求复数 的辐角主值.解:由 ,得 . 于是 . 例5 如图,在平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对角线AC将△ABC折起,使二面角
B-AC-D成直二面角.
(Ⅰ)求证:AB⊥面BCD;
(Ⅱ)求二面角B—AD—C
的大小;
(Ⅲ)求点C到平面ABD的
距离. 解:(Ⅰ)由∠ABC=90°,得
AB⊥BC.由于AB=BC=a,
故∠BCA=45°. 又在平面图形中,∠C=135°,
故在三棱锥中,∠ACD=90°.
从而CD⊥AC. 又因为二面角B-AC-D是直二面角,
所以 面ABC⊥面ACD,于是CD⊥面ABC,
因此 CD⊥AB .
故 AB⊥面BCD. (Ⅱ)过点B 作BE⊥AC于E,则BE = AE = CE,BE⊥面ACD. 过E 作EF⊥AD于F,连BF,由三垂线定理,知BF⊥AD.因此∠BFE是
二面角B—AD—C的平面角. 在Rt△ABC 中,由于AB=BC=a ,故. 在Rt△ACD中,由于CD=a,
故 . 又△AEF ∽△ADC,所以 ,
故 . 在Rt△BEF中, ,
故∠BFE=60°.
即二面角B-AD-C为60°. (Ⅲ)易知
.
又
所以 由于
设C到平面ABD的距离为d
则
即
解得
即点C到平面ABD的距离是 . 例6 某海军基地的三艘舰艇在某海域的A、B、C三处定点执行任务.已知A在B的正东方向,且A、B相距6千米.C在B的北偏西30°,B、C相距4千米.某时刻A处舰艇收到该海域内P处一渔船以每秒1千米的传播速度发出的“由于机器故障无法航行急需救助”的信号,4秒钟后B、C两处的舰艇才同时收到这一信号.现A处舰艇奉命前去救助,求A处舰艇前去救助时航向的方位角. 例6 某海军基地的三艘舰艇在某海域的A、B、C三处定点执行任务.已知A在B的正东方向,且A、B相距6千米.C在B的北偏西30°,B、C相距4千米.某时刻A处舰艇收到该海域内P处一渔船以每秒1千米的传播速度发出的“由于机器故障无法航行急需救助”的信号,4秒钟后B、C两处的舰艇才同时收到这一信号.现A处舰艇奉命前去救助,求A处舰艇前去救助时航向的方位角. 解:以BA所在直线为x轴,线段BA的中点为原点,正东、正北方向分别为x轴、y轴的正方向建立直角坐标系(如图), 则A(3,0),B(-3,0), =4. 过C作CM⊥x轴于M,由于C在B的北偏西 30°,故∠CBM = 60°. ∴ ,
,
于是得 .
由于B处舰艇收到信号比A处舰艇收到信号迟4秒,且信号传播速度为每秒1千米,
故|PB|-|PA|= 4. 因此,P点在以A、B为焦点的双曲
线的右支上,且 2a = 4,2c = 6,从而
a = 2,c = 3,b2 = c2-a2 = 5.
所以,双曲线的方程为
① 因为B、C两处舰艇同时收到P处渔船发出的呼救信号,所以|PB|=|PC|,于是点P必在线段BC 的垂直平分线上. 由点斜式得直线PQ 的方程为
整理,得 . ② 过P作PQ⊥BC于Q,则Q必为BC的中
点.故得 ,
.
联立①、②,注意到x≥2,解得x = 8,
,于是得 .
设PA的倾斜角为?,则
.
故 .因此所求的方位角为30°. 解好解答题中综合性难题的对策 一、“翻译”转化,弄清已知,明确
目标,理顺思路.
二、辨别题型,设计方案,寻求最
佳解法.
三、解前估测猜想,解后检验思考,
总结经验教训,分析错误原因.
例1.已知函数,f (x)=ax2-1 (a∈R,x∈R),集合
且A=B≠?.求a的取值范围.
抛物线y= ax2-1 与直线y=x的交点的横坐标. 方程ax2-1 =x的实根 方程a (ax2-1)2-1=x的实根 方程组 的解中x的值 曲线y=ax2-1与曲线x=ay2-1的公共点的横坐标. A=B≠? 集合A、B中元素都相同且不是空集 方程ax2-1=x有实根,且与方程
a (ax2-1)2-1=x同解 曲线y= ax2-1与y =x有交点,且
交点就是曲线y= ax2-1与x= ay2-1的交点. 由A≠?,得到a的一个范围;
证明 ;解题方案一(3) 由于 ,说明四次方程
a (ax2-1)2-1- x=0
左边的四次式必能因式分解,分解 出一个二次式ax2-1-x 与另一个二次式的乘积;
利用A=B再得出a的另一个范围.
(1) A≠? y=ax2-1与y=x有公共点;解题方案二 (2) A=B 曲线y= ax2-1上不存在两个
不同点关于直线y=x对称. 曲线y= ax2-1上斜率为-1 的平
行弦中点轨迹与y = x 没有公共点.
解题方案二解:(1) 由A≠?,知
方程ax2-x-1=0有实根, 当a=0时,该方程有实根; 当a≠0时,由△1≥0,得
1+4a≥0,
即 (a≠0),
综上,得 .(2) f [f (x)]=x即
a (ax2-1)2-1-x=0
a3x4-2a2x2-x+a-1=0
(ax2-x-1)(a2x2+ax-a+1)=0.
A=B当且仅当方程
a2x2+ax-a+1=0 ②
无实根或方程②的实根都是方程
ax2-x-1=0 ① 的实根,
方程①与②的实根不都相同 . 当△2=a2-4a2(-a+1)<0,即
时方程②无实根;
当△2=0,即 时,方程②有
重根 ,恰是方程①的两根之一;
∴ 当且仅当 时A=B.
综上,
A=B≠?时a的取值范围是 . 练习题 1 函数y =ax2-2的图像上存在不同两点关于直线y =x对称,求a的取值范围.例2.已知无穷数列{an}的每一项都是正
整数,且 ,
an
an恒为一个常数?分析: 假设存在自然数k, ,那
么 ,
于是 ,
,
……
∵ 数列各项都是自然数,
∴
设 ,则 ,这与已知矛盾. (2) 如果存在自然数n, ,
那么
又因为 ,
∴ ,
从而
如果对于任意自然数n,都有 ,
那么因为已知此数列每一项都是自然数,
所以 ,从而
设 M 的整数部分是t,则
,
这与数列每一项都小于M 是矛盾的.
综上可知,存在自然数m,当n≥m 时,
an恒为一常数. 已知无穷数列{an}的每一项都是正整数,且 (n∈N),集合P={(x,y)|x=n,y=an,n∈N}.
求证:集合P 中有无穷多个点在一直线上.
练习题 2例3.已知抛物线顶点在x轴上,以y轴为准线,点A(4,0)到此抛物线上动点 P的距离的最小值为2,求此抛物线的方程.解:设所求抛物线顶点为(a,0),那么方 程为y2=4a (x-a).
设抛物线上动点P的坐标为 (x,y),
解得,
∴ 抛物线方程为
或 代数解法所得结论与解前估测的结
果不符,孰对孰错?
,
当4-2a≥a 即 时,
,
得 ;
分 析当 ,则x=a时|PA|最小,
∴ 得a=2或a=6. 综上,所求抛物线方程为
,
y2 =8(x-2),y2=24(x-6). 是否存在同时满足下列条件的双曲
线,若存在,求出方程;若不存在,说
明理由:
(1) 渐近线方程为x+2y=0 及x-2y=0 ;
(2) 点A (5,0)到双曲线上动点P 的距离
最小值为 .练习题 3 例4.设二次函数f (x)=ax2+bx+c (a>0),方
程f (x)-x=0的两个根x1,x2满足
(1) 当x∈(0,x1)时,证明x
因x1,x2是方程f (x)-x=0的根,
所以 .
当 时, ,
又a>0,故 ,
即x
∴ ,
,
∴ ,
(2) 依题意, .
∵ x1,x2是方程ax2+(b-1)x+c=0的根,
∴ .
∵ ,
∴ . 证明二:
由(2)的结论证明(1)的 .
∵ x=x0是f (x)图像的对称轴,且a>0,
∴ f (x)在 上递增,在
上递减.
当 时,f (x)
∴ ,
∴ .
综上两种情况,当 时,
.
