直线与椭圆的位置关系[上学期]
文档属性
| 名称 | 直线与椭圆的位置关系[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 108.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-07 00:00:00 | ||
图片预览




文档简介
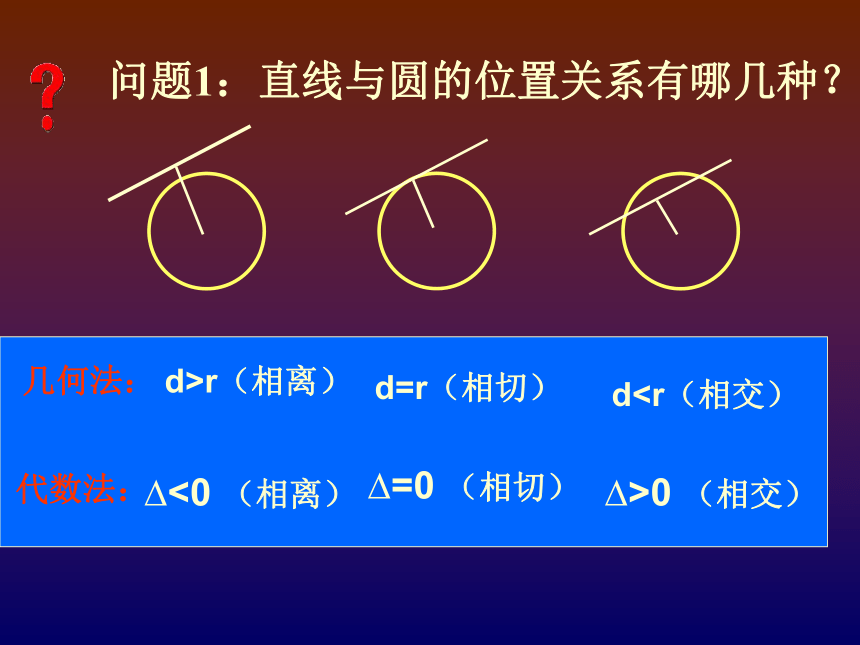
课件13张PPT。直线与椭圆的位置关系怎么判断它们之间的位置关系?问题1:直线与圆的位置关系有哪几种?d>r(相离)d0 (相交)?<0 (相离)?=0 (相切)几何法:代数法:点与椭圆的位置关系及判断1.点在椭圆外2.点在椭圆上3.点在椭圆内点P(x0,y0)
椭圆问题3:怎么判断它们之间的位置关系?能用几何法吗?问题2:椭圆与直线的位置关系?不能!所以只能用代数法----求解直线与二次曲线有关问题的通法。因为他们不像圆一样有统一的半径。例1:已知直线y=x- 与椭圆x2+4y2=2 ,判断它们的位置关系。解:联立方程组消去y?=36>0因为所以,方程(1)有两个根,那么,相交所得的弦AB的长是多少?弦长公式:则原方程组有两组解….----- (1)
由韦达
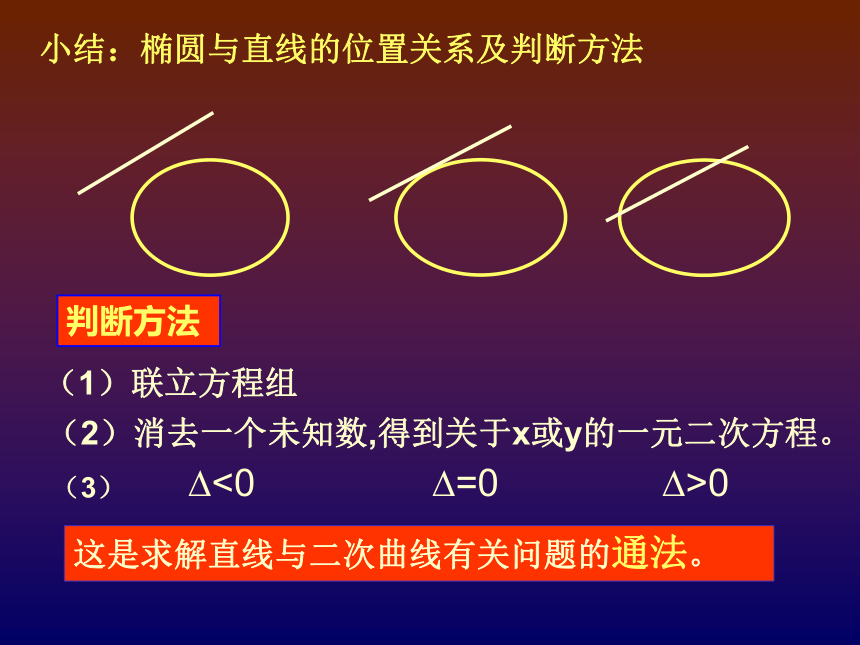
定理小结:椭圆与直线的位置关系及判断方法判断方法这是求解直线与二次曲线有关问题的通法。?<0?=0?>0(1)联立方程组(2)消去一个未知数,得到关于x或y的一元二次方程。(3)1、直线与圆相交的弦长A(x1,y1)小结:直线与二次曲线相交弦长的求法dr2、直线与其它二次曲线相交的弦长(1)联立方程组(2)消去一个未知数(3)利用弦长公式:|AB| = k 表示弦的斜率,x1、x2、y1、y2表示弦的端点坐标,一般由韦达定理求得 x1+ x2 与 y1+ y2通法B(x2,y2) = 设而不求椭圆 的两个焦点为F1 、F2 ,过左焦点作直线与椭圆交于A,B 两点,若直线AB的倾角为30度,求△ AB F2 的面积。例2法一:利用d联立方程组{d=2|AB|=过F2作到直线AB的垂线,设距离为d已知椭圆 ,若它的一条弦AB被M(1,1)平分,求AB所在的直线方程;(2)求过点M(1,1)的弦的中点的轨迹。解:设所求直线AB的方程为直线AB的方程为:(方法二)解:设直线AB的方程为:设而不求3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及等价条件;2、弦长的计算方法:
(1)垂径定理:|AB|= (只适用于圆)
(2)弦长公式:
|AB|=
= (适用于任何曲线) 小 结1、求椭圆 被过右焦点且垂直于x轴
的直线所截得的弦长。通径3、中心在原点,一个焦点为F(0, )的椭圆被
直线 y=3x-2所截得弦的中点横坐标是1/2,求椭圆
方程。练习2。y=kx+1与椭圆 恰有公共点,则m的范围( )
A、(0,1) B、(0,5 )
C、[ 1,5)∪(5,+ ∞ ) D、(1,+ ∞ )C
椭圆问题3:怎么判断它们之间的位置关系?能用几何法吗?问题2:椭圆与直线的位置关系?不能!所以只能用代数法----求解直线与二次曲线有关问题的通法。因为他们不像圆一样有统一的半径。例1:已知直线y=x- 与椭圆x2+4y2=2 ,判断它们的位置关系。解:联立方程组消去y?=36>0因为所以,方程(1)有两个根,那么,相交所得的弦AB的长是多少?弦长公式:则原方程组有两组解….----- (1)
由韦达
定理小结:椭圆与直线的位置关系及判断方法判断方法这是求解直线与二次曲线有关问题的通法。?<0?=0?>0(1)联立方程组(2)消去一个未知数,得到关于x或y的一元二次方程。(3)1、直线与圆相交的弦长A(x1,y1)小结:直线与二次曲线相交弦长的求法dr2、直线与其它二次曲线相交的弦长(1)联立方程组(2)消去一个未知数(3)利用弦长公式:|AB| = k 表示弦的斜率,x1、x2、y1、y2表示弦的端点坐标,一般由韦达定理求得 x1+ x2 与 y1+ y2通法B(x2,y2) = 设而不求椭圆 的两个焦点为F1 、F2 ,过左焦点作直线与椭圆交于A,B 两点,若直线AB的倾角为30度,求△ AB F2 的面积。例2法一:利用d联立方程组{d=2|AB|=过F2作到直线AB的垂线,设距离为d已知椭圆 ,若它的一条弦AB被M(1,1)平分,求AB所在的直线方程;(2)求过点M(1,1)的弦的中点的轨迹。解:设所求直线AB的方程为直线AB的方程为:(方法二)解:设直线AB的方程为:设而不求3、弦中点问题的两种处理方法:
(1)联立方程组,消去一个未知数,利用韦达定理;
(2)设两端点坐标,代入曲线方程相减可求出弦的斜率。 1、直线与椭圆的三种位置关系及等价条件;2、弦长的计算方法:
(1)垂径定理:|AB|= (只适用于圆)
(2)弦长公式:
|AB|=
= (适用于任何曲线) 小 结1、求椭圆 被过右焦点且垂直于x轴
的直线所截得的弦长。通径3、中心在原点,一个焦点为F(0, )的椭圆被
直线 y=3x-2所截得弦的中点横坐标是1/2,求椭圆
方程。练习2。y=kx+1与椭圆 恰有公共点,则m的范围( )
A、(0,1) B、(0,5 )
C、[ 1,5)∪(5,+ ∞ ) D、(1,+ ∞ )C
