椭圆性质1[上学期]
图片预览





文档简介
课件16张PPT。椭圆的几何性质复习思考2.平面解析几何研究的主要问题是什么? 答:1)根据已知条件,求出表示平面曲线的
方程。
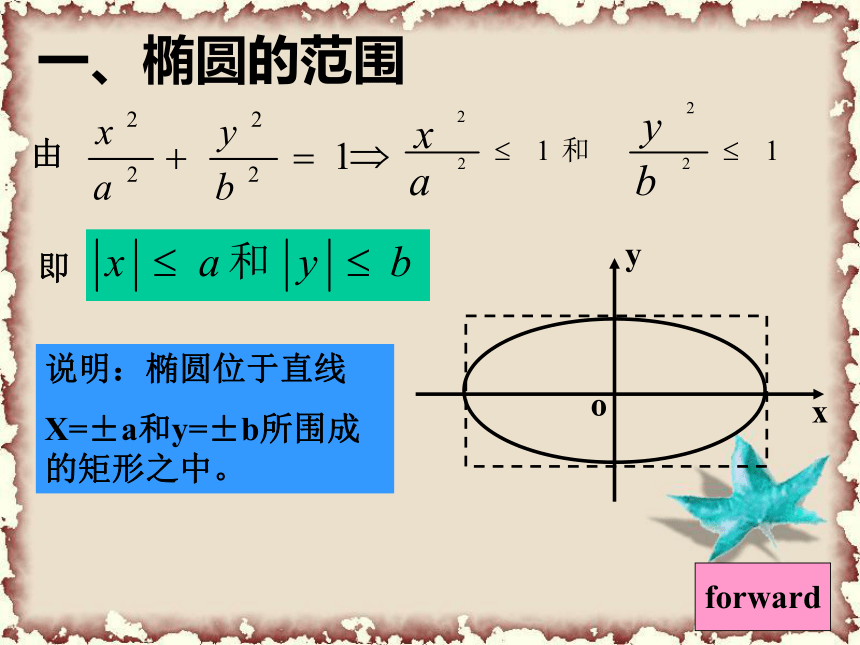
2)通过方程,研究平面曲线的性质。一、椭圆的范围说明:椭圆位于直线
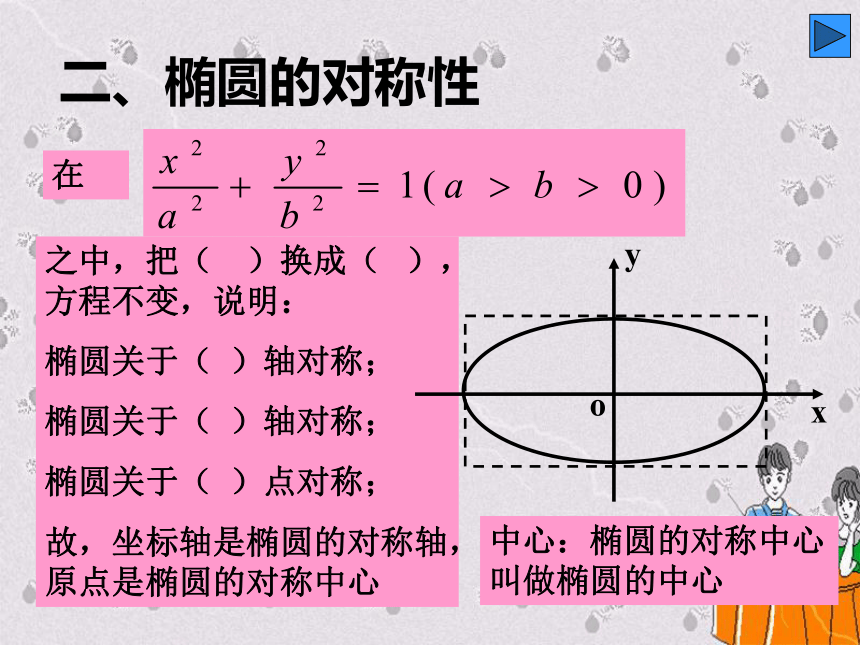
X=±a和y=±b所围成的矩形之中。forward二、椭圆的对称性中心:椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点( , ),
令 y=0,得 x=?说明椭圆与 x轴的交点( , )*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。︱ ︱
F1 F2
0 ±b±a 0四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:
因为 a > c > 0,所以1 >e >0[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,从而 b就越小(?),椭圆就越扁(?)
2)e 越接近 0,c 就越接近 0,从而 b就越大(?),椭圆就越圆(?)
3)特例:e =0,则 a = b,则 c=0,两个焦点重合,椭圆方程变为(?)
[1]椭圆标准方程所表示的椭圆的存在范围是什么?[2]上述方程表示的椭圆有几个对称轴?几个对称中心?[3]椭圆有几个顶点?顶点是谁与谁的交点?[4]对称轴与长轴、短轴是什么关系?[5]2a 和 2b是什么量? a和 b是什么量?[6]关于离心率讲了几点?回 顾小结一:基本元素{1}基本量:a、b、c、e、(共四个量){2}基本点:顶点、焦点、中心(共七个点){3}基本线:对称轴(共两条线)请考虑:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)∣ ∣
F1 F2_
_
A2A1B1B20关于x轴,y轴,原点
对称。关于x轴,y轴,原点对称。例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标,并用描点法画出它的图形.解:把已知方程化成标准方程这里,课堂练习(1)、说出下列椭圆的范围、对称性、顶点坐标
离心率?
(Ⅰ)
(Ⅱ)
(2)、下列方程所表示的曲线中,关于x轴和y 轴
都对称的是( )
A、X2=4Y B、X2+2XY+Y=0 C、X2-4Y2=X
D、9X2+Y2=4D题型{1}由椭圆标准方程求基本元素说明:例1是一种常见的题型,在以后的有关圆锥曲线的问题中,经常要用到这种题型,说它是一种题型不如说它是一种要经常用到的“基本计算”例2、求适合下列条件的椭圆的标准方程: (1)经过点P(-3,0),Q(0,-2); (2)长轴的长等于20,离心率等于3/5; 课堂练习:作业P47 5 6 中华一题 p29--30
方程。
2)通过方程,研究平面曲线的性质。一、椭圆的范围说明:椭圆位于直线
X=±a和y=±b所围成的矩形之中。forward二、椭圆的对称性中心:椭圆的对称中心叫做椭圆的中心三、椭圆的顶点在中,令 x=0,得 y=?,说明椭圆与 y轴的交点( , ),
令 y=0,得 x=?说明椭圆与 x轴的交点( , )*顶点:椭圆与它的对称轴的四个交点,叫做椭圆的顶点。
*长轴、短轴:线段A1A2、B1B2分别叫做椭圆的长轴和短轴。
a、b分别叫做椭圆的长半轴长和短半轴长。︱ ︱
F1 F2
0 ±b±a 0四、椭圆的离心率离心率:椭圆的焦距与长轴长的比:叫做椭圆的离心率。[1]离心率的取值范围:
因为 a > c > 0,所以1 >e >0[2]离心率对椭圆形状的影响:
1)e 越接近 1,c 就越接近 a,从而 b就越小(?),椭圆就越扁(?)
2)e 越接近 0,c 就越接近 0,从而 b就越大(?),椭圆就越圆(?)
3)特例:e =0,则 a = b,则 c=0,两个焦点重合,椭圆方程变为(?)
[1]椭圆标准方程所表示的椭圆的存在范围是什么?[2]上述方程表示的椭圆有几个对称轴?几个对称中心?[3]椭圆有几个顶点?顶点是谁与谁的交点?[4]对称轴与长轴、短轴是什么关系?[5]2a 和 2b是什么量? a和 b是什么量?[6]关于离心率讲了几点?回 顾小结一:基本元素{1}基本量:a、b、c、e、(共四个量){2}基本点:顶点、焦点、中心(共七个点){3}基本线:对称轴(共两条线)请考虑:基本量之间、基本点之间、基本线之间以及它们相互之间的关系(位置、数量之间的关系)∣ ∣
F1 F2_
_
A2A1B1B20关于x轴,y轴,原点
对称。关于x轴,y轴,原点对称。例1 求椭圆 16 x2 + 25y2 =400的长轴和短轴的长、离心率、焦点和顶点坐标,并用描点法画出它的图形.解:把已知方程化成标准方程这里,课堂练习(1)、说出下列椭圆的范围、对称性、顶点坐标
离心率?
(Ⅰ)
(Ⅱ)
(2)、下列方程所表示的曲线中,关于x轴和y 轴
都对称的是( )
A、X2=4Y B、X2+2XY+Y=0 C、X2-4Y2=X
D、9X2+Y2=4D题型{1}由椭圆标准方程求基本元素说明:例1是一种常见的题型,在以后的有关圆锥曲线的问题中,经常要用到这种题型,说它是一种题型不如说它是一种要经常用到的“基本计算”例2、求适合下列条件的椭圆的标准方程: (1)经过点P(-3,0),Q(0,-2); (2)长轴的长等于20,离心率等于3/5; 课堂练习:作业P47 5 6 中华一题 p29--30
