椭圆性质4[上学期]
图片预览



文档简介
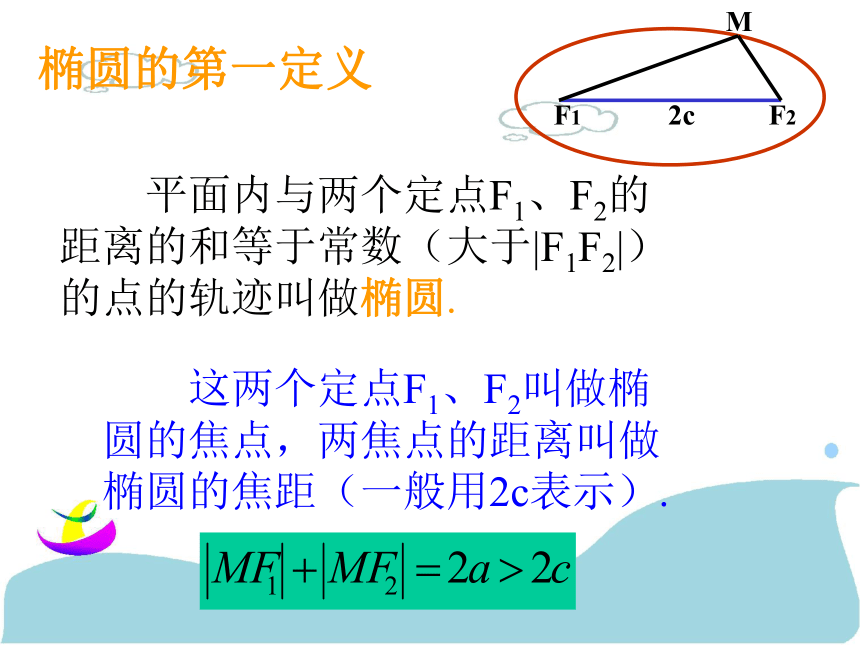
课件14张PPT。椭圆的简单几何性质 平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点F1、F2叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距(一般用2c表示).椭圆的第一定义动点M与一个定点的距离和它到一条定直线
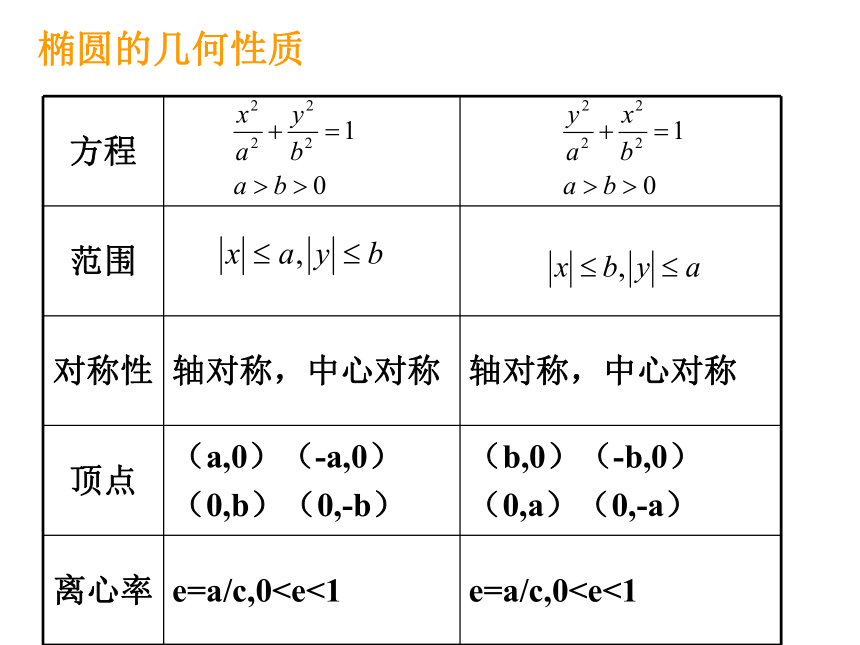
的距离之比是常数 (a>c>0),则动点M的轨迹叫做椭圆.这个定点叫做椭圆的一个焦点,这条定直线l叫做椭圆的准线,准线与长轴所在直线互相垂直。(椭圆的第二定义)椭圆的几何性质练习1、中点在原点,长轴长是短轴长的2倍,一条准线的方程x=4,椭圆的方程是______
2、椭圆的两个焦点三等分它两准线间的距离,则椭圆的离心率_______
3、椭圆的中心在原点,焦点在坐标轴上 ,准线方程y=18,y=-18,椭圆上一点到两焦点的距离分别是10和14,则椭圆的方程_______
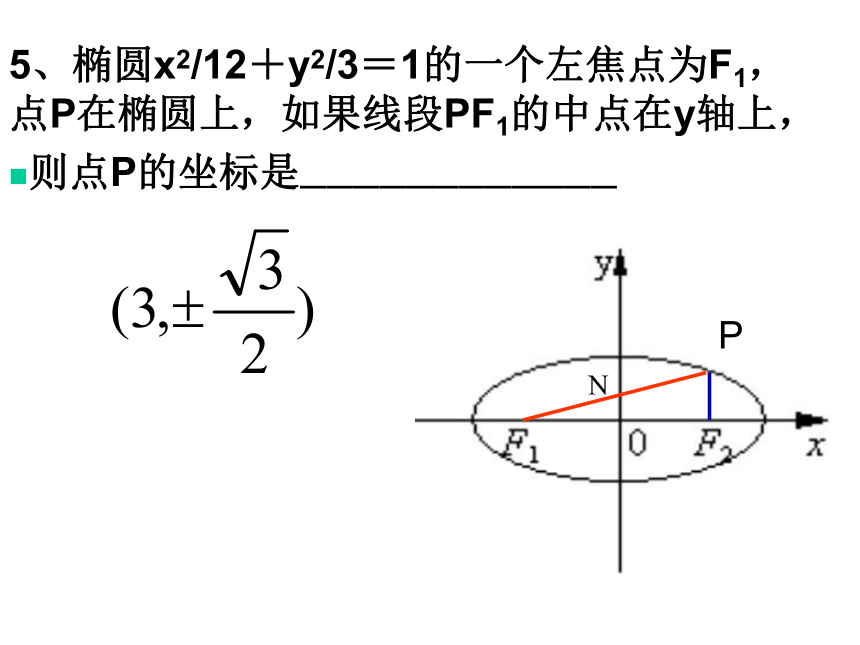
4、已知P是9x2+25y2=900,若P到椭圆右准线的距离是17/2,则P到左焦点的距离是_____5、椭圆x2/12+y2/3=1的一个左焦点为F1,点P在椭圆上,如果线段PF1的中点在y轴上,
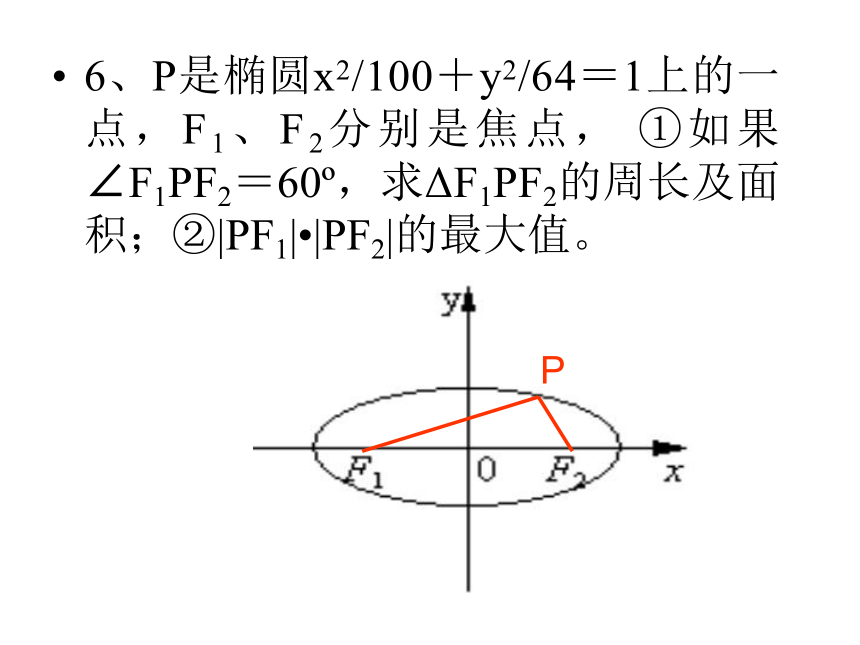
则点P的坐标是————————————P N6、P是椭圆x2/100+y2/64=1上的一点,F1、F2分别是焦点, ①如果∠F1PF2=60o,求ΔF1PF2的周长及面积;②|PF1|?|PF2|的最大值。 PMAKFOxyl评述: (1)以上解法就是椭圆第二定义的巧用,将问题转化成点到直线的距离去求,就可以使题目变得简单易解了。
(2)一般地,如果遇到一个定点到定直线问题应联想到椭圆第二定义。PPOOyyxxF2F1F2F1总结归纳思想方法:坐标法、待定系数法、平方 法、数形结合
技巧:充分利用椭圆的定义解题
知识点:定义、标准方程、几何性质作业:2、椭圆两焦点和中心将两准线间的距离四等分,则一焦点与短轴连线的夹角是( )
A、45o B、60o C、90o D、120o3、点M与定点F(8,0)的距离和它到
定直线 x=25/2的距离之比为4∶5,
则点M的轨迹方程是_________。yxpQOFQ/P/5、P47 7
的距离之比是常数 (a>c>0),则动点M的轨迹叫做椭圆.这个定点叫做椭圆的一个焦点,这条定直线l叫做椭圆的准线,准线与长轴所在直线互相垂直。(椭圆的第二定义)椭圆的几何性质练习1、中点在原点,长轴长是短轴长的2倍,一条准线的方程x=4,椭圆的方程是______
2、椭圆的两个焦点三等分它两准线间的距离,则椭圆的离心率_______
3、椭圆的中心在原点,焦点在坐标轴上 ,准线方程y=18,y=-18,椭圆上一点到两焦点的距离分别是10和14,则椭圆的方程_______
4、已知P是9x2+25y2=900,若P到椭圆右准线的距离是17/2,则P到左焦点的距离是_____5、椭圆x2/12+y2/3=1的一个左焦点为F1,点P在椭圆上,如果线段PF1的中点在y轴上,
则点P的坐标是————————————P N6、P是椭圆x2/100+y2/64=1上的一点,F1、F2分别是焦点, ①如果∠F1PF2=60o,求ΔF1PF2的周长及面积;②|PF1|?|PF2|的最大值。 PMAKFOxyl评述: (1)以上解法就是椭圆第二定义的巧用,将问题转化成点到直线的距离去求,就可以使题目变得简单易解了。
(2)一般地,如果遇到一个定点到定直线问题应联想到椭圆第二定义。PPOOyyxxF2F1F2F1总结归纳思想方法:坐标法、待定系数法、平方 法、数形结合
技巧:充分利用椭圆的定义解题
知识点:定义、标准方程、几何性质作业:2、椭圆两焦点和中心将两准线间的距离四等分,则一焦点与短轴连线的夹角是( )
A、45o B、60o C、90o D、120o3、点M与定点F(8,0)的距离和它到
定直线 x=25/2的距离之比为4∶5,
则点M的轨迹方程是_________。yxpQOFQ/P/5、P47 7
