椭圆及标准方程(一二)[上学期]
文档属性
| 名称 | 椭圆及标准方程(一二)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 711.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2006-11-07 17:12:00 | ||
图片预览




文档简介
课件28张PPT。椭圆及标准方程
1、圆锥曲线的定义: 通常把椭圆、双曲线、
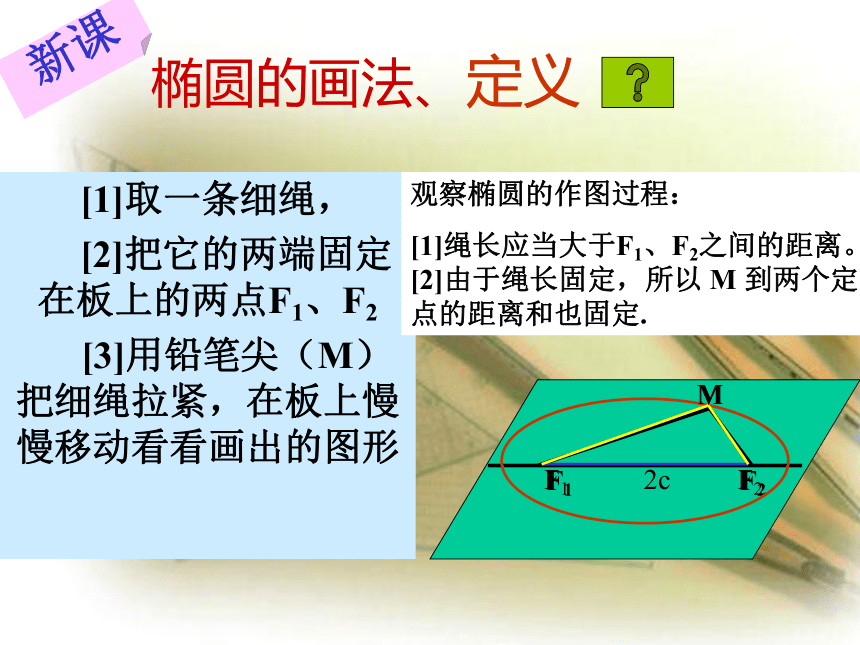
抛物线统称为圆锥曲线。导入2、天体运行的轨道 椭圆生活中的椭圆罐车的横截面椭圆的画法、定义 [1]取一条细绳,
[2]把它的两端固定在板上的两点F1、F2
[3]用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形观察椭圆的作图过程:
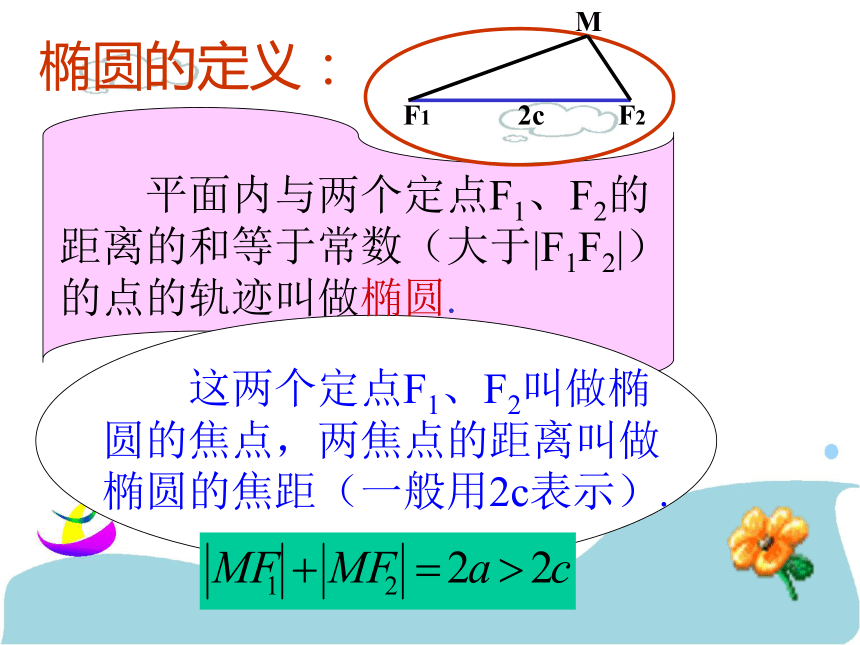
[1]绳长应当大于F1、F2之间的距离。[2]由于绳长固定,所以 M 到两个定点的距离和也固定.新课椭圆的定义: 平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点F1、F2叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距(一般用2c表示).小结一:满足哪几个条件的动点的轨迹叫做椭圆?[1]平面上----这是大前提
[2]动点 M 到两个定点 F1、F2 的距离之和是常数 2a
[3]常数 2a 要大于焦距 2C[二]椭圆方程推导的准备[1]建系,取点
[2]列等式
[3]等式坐标化
[4]化简
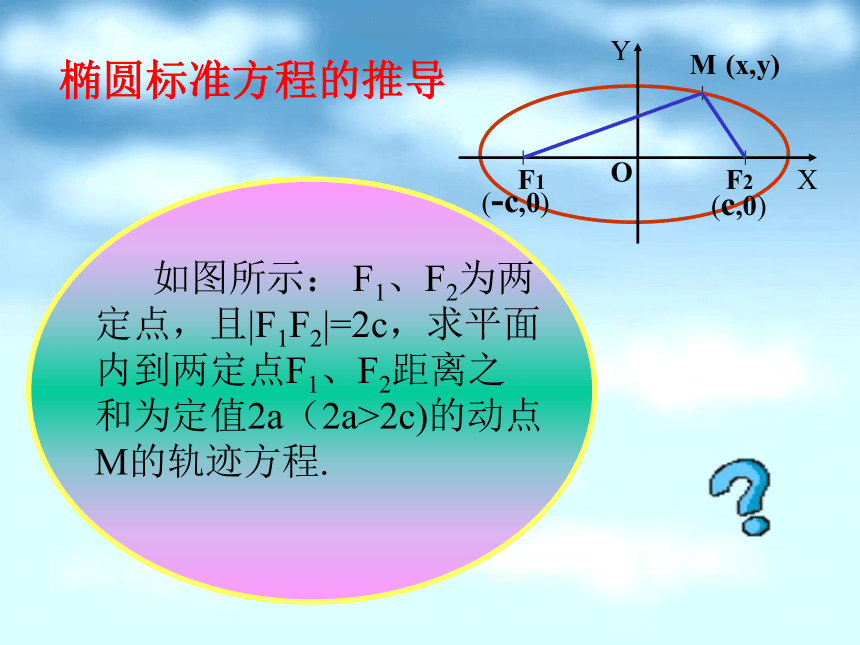
[5]检验,证明建系的一般原则? 如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程.椭圆标准方程的推导 解:以F1F2所在直线为x轴,F1F2 的中点为原点建立平面直角坐标系,则焦点F1、F2的坐标分别为(-c,0)、 (c,0).设M(x,y)为所求轨迹上的任意一点,则:|MF1|+ |MF2|=2a两边平方得:a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即:(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c,即a>c,所以a2-c2>0,
令a2-c2=b2,其中b>0,代入
上式可得:b2x2+a2y2=a2b2两边同时除以a2b2得:(a>b>0)
焦点在y轴上,焦点F1 ( 0 , -c),
F2 ( 0 , c),其中c2=a2-b2 .
焦点在x轴上,焦点F1 (-c,0),
F2 (c,0),其中c2=a2-b2 .
椭圆的标准方程椭圆的标准方程的再认识:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1;(2)椭圆的标准方程中三个参数a、b、c始终满足c2 = a2 -b2
(不要与勾股定理a2 +b2=c2 混淆);
(3)由椭圆的标准方程可以求出三个参数a、b、c的值;(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
哪一个轴上 . 1、 判定下列椭圆的焦点在?轴,并指明a2、b2,写出焦点坐标答:在 X 轴。(-3,0)和(3,0)答:在 y 轴。(0,-5)和(0,5)答:在y 轴。(0,-1)和(0,1)判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。巩固概念 2、将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标在上述方程中,A、B、C满足什么条件,就表示椭圆?
答: A、B、C同号,且A不等于B。例题精析543(-3,0) 、(3,0)
62021(0,-1)、(0,1)2例2、求满足下列条件的椭圆的标准方程: (1)两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10. 解:因为椭圆的焦点在X轴上,所以可设它的方程为:∵2a=10,2c=8∴a=5,c=4 ∴b2=a2-c2=52-42=9所以椭圆的标准方程为: 求椭圆的方程 (2)两焦点的坐标分别是(0,-2)、(0,2),并且椭圆经过点解:因为椭圆的焦点在y轴上,所以可设它的方程为:由椭圆的定义知,又c=2所以椭圆的标准方程为:在求椭圆的标准方程时,应从“定位”与“定量”两个方面去考虑,“定位”是指确定焦点所在的坐标轴,以判断方程的形式;“定量”是指确定方程中的 与 的具体数值,常常通过系数法去求.小结1、求满足下列条件的椭圆的标准方程:(1)满足a=4,b=1,焦点在X轴上的椭圆的标准方程为____________ (2)满足a=4,c= ,焦点在Y轴上的椭圆的标准方程为____________练习:有共同的焦点。 例3、已知B、C是两个定点, | BC|=6,
且△ABC的周长等于16,求顶点A的轨迹
方程。2、动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为----------------( )
A.椭圆
B.线段F1F2
C.直线F1F2
D.不能确定
B练习:例3:若方程4x2+kx2=1表示的曲线是焦点在y轴上的椭圆,求k的取值范围.解:由 4x2+ky2=1因为方程表示的曲线是焦点在y轴上的椭圆即:0中华一题 P26 13
1、圆锥曲线的定义: 通常把椭圆、双曲线、
抛物线统称为圆锥曲线。导入2、天体运行的轨道 椭圆生活中的椭圆罐车的横截面椭圆的画法、定义 [1]取一条细绳,
[2]把它的两端固定在板上的两点F1、F2
[3]用铅笔尖(M)把细绳拉紧,在板上慢慢移动看看画出的图形观察椭圆的作图过程:
[1]绳长应当大于F1、F2之间的距离。[2]由于绳长固定,所以 M 到两个定点的距离和也固定.新课椭圆的定义: 平面内与两个定点F1、F2的距离的和等于常数(大于|F1F2|)的点的轨迹叫做椭圆. 这两个定点F1、F2叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距(一般用2c表示).小结一:满足哪几个条件的动点的轨迹叫做椭圆?[1]平面上----这是大前提
[2]动点 M 到两个定点 F1、F2 的距离之和是常数 2a
[3]常数 2a 要大于焦距 2C[二]椭圆方程推导的准备[1]建系,取点
[2]列等式
[3]等式坐标化
[4]化简
[5]检验,证明建系的一般原则? 如图所示: F1、F2为两定点,且|F1F2|=2c,求平面内到两定点F1、F2距离之和为定值2a(2a>2c)的动点M的轨迹方程.椭圆标准方程的推导 解:以F1F2所在直线为x轴,F1F2 的中点为原点建立平面直角坐标系,则焦点F1、F2的坐标分别为(-c,0)、 (c,0).设M(x,y)为所求轨迹上的任意一点,则:|MF1|+ |MF2|=2a两边平方得:a4-2a2cx+c2x2=a2x2-2a2cx+a2c2+a2y2即:(a2-c2)x2+a2y2=a2(a2-c2)因为2a>2c,即a>c,所以a2-c2>0,
令a2-c2=b2,其中b>0,代入
上式可得:b2x2+a2y2=a2b2两边同时除以a2b2得:(a>b>0)
焦点在y轴上,焦点F1 ( 0 , -c),
F2 ( 0 , c),其中c2=a2-b2 .
焦点在x轴上,焦点F1 (-c,0),
F2 (c,0),其中c2=a2-b2 .
椭圆的标准方程椭圆的标准方程的再认识:(1)椭圆标准方程的形式:左边是两个分式的平方和,右边是1;(2)椭圆的标准方程中三个参数a、b、c始终满足c2 = a2 -b2
(不要与勾股定理a2 +b2=c2 混淆);
(3)由椭圆的标准方程可以求出三个参数a、b、c的值;(4)椭圆的标准方程中,x2与y2的分母哪一个大,则焦点在
哪一个轴上 . 1、 判定下列椭圆的焦点在?轴,并指明a2、b2,写出焦点坐标答:在 X 轴。(-3,0)和(3,0)答:在 y 轴。(0,-5)和(0,5)答:在y 轴。(0,-1)和(0,1)判断椭圆标准方程的焦点在哪个轴上的准则:
焦点在分母大的那个轴上。巩固概念 2、将下列方程化为标准方程,并判定焦点在哪个轴上,写出焦点坐标在上述方程中,A、B、C满足什么条件,就表示椭圆?
答: A、B、C同号,且A不等于B。例题精析543(-3,0) 、(3,0)
62021(0,-1)、(0,1)2例2、求满足下列条件的椭圆的标准方程: (1)两焦点的坐标分别是(-4,0)、(4,0),椭圆上一点P到两焦点距离之和等于10. 解:因为椭圆的焦点在X轴上,所以可设它的方程为:∵2a=10,2c=8∴a=5,c=4 ∴b2=a2-c2=52-42=9所以椭圆的标准方程为: 求椭圆的方程 (2)两焦点的坐标分别是(0,-2)、(0,2),并且椭圆经过点解:因为椭圆的焦点在y轴上,所以可设它的方程为:由椭圆的定义知,又c=2所以椭圆的标准方程为:在求椭圆的标准方程时,应从“定位”与“定量”两个方面去考虑,“定位”是指确定焦点所在的坐标轴,以判断方程的形式;“定量”是指确定方程中的 与 的具体数值,常常通过系数法去求.小结1、求满足下列条件的椭圆的标准方程:(1)满足a=4,b=1,焦点在X轴上的椭圆的标准方程为____________ (2)满足a=4,c= ,焦点在Y轴上的椭圆的标准方程为____________练习:有共同的焦点。 例3、已知B、C是两个定点, | BC|=6,
且△ABC的周长等于16,求顶点A的轨迹
方程。2、动点P到两定点F1(-4,0),F2(4,0)的距离之和为8,则动点P的轨迹为----------------( )
A.椭圆
B.线段F1F2
C.直线F1F2
D.不能确定
B练习:例3:若方程4x2+kx2=1表示的曲线是焦点在y轴上的椭圆,求k的取值范围.解:由 4x2+ky2=1因为方程表示的曲线是焦点在y轴上的椭圆即:0
