椭圆性质3[上学期]
图片预览





文档简介
课件14张PPT。高二数学组梁家斌椭圆的简单几何性质学习目标 1、进一步理解并掌握椭圆的定义、标准方程2、能根据条件求出椭圆的标准方程
3、进一步理解a、b、c、e的几何意义,会用几何性质解决有关问题
4、在坐标法的基础上掌握点的轨迹条件满足某曲线的定义时,用待定系数法求其方程1、椭圆的定义运用:
⑴ΔABC的周长为20,且B (-4,0),C(4,0),则点A的轨迹方程是_____________.
⑵已知A(-1,0),B(1,0),线段CA、AB、CB的长成等差数列,则点C的轨迹方程是_____________.
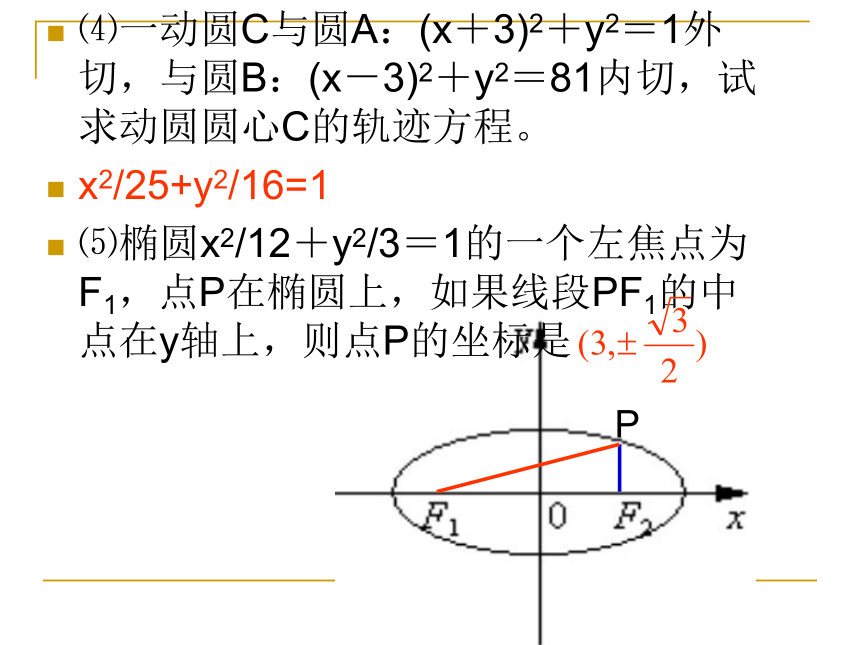
⑶过点A(0,2),且与圆B:x2+(y+2)2=36内切的动圆圆心C的轨迹方程是__________.x2/36+y2/20=1(y≠0)x2/4+y2/3=1x2/5+y2/9=1⑷一动圆C与圆A:(x+3)2+y2=1外切,与圆B:(x-3)2+y2=81内切,试求动圆圆心C的轨迹方程。
x2/25+y2/16=1
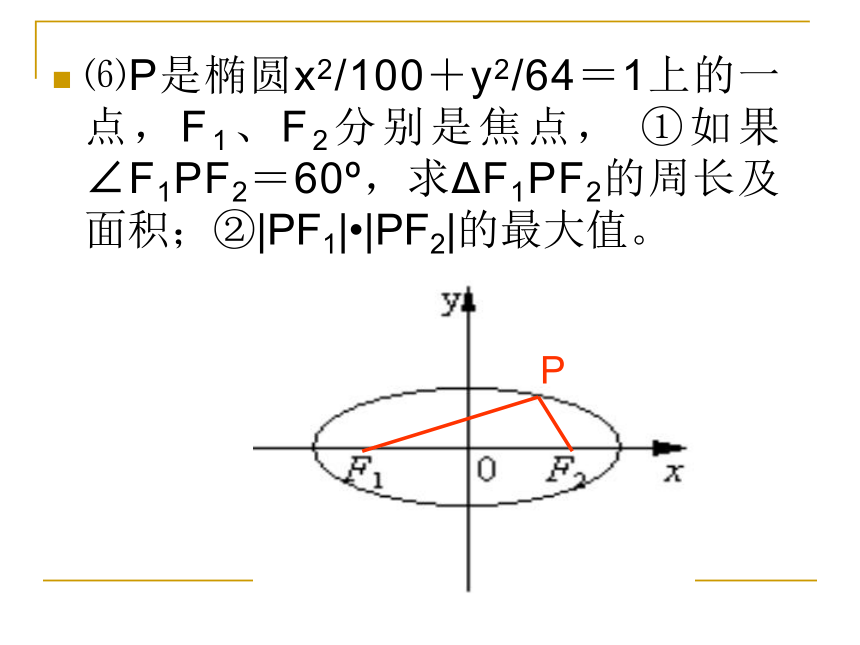
⑸椭圆x2/12+y2/3=1的一个左焦点为F1,点P在椭圆上,如果线段PF1的中点在y轴上,则点P的坐标是P⑹P是椭圆x2/100+y2/64=1上的一点,F1、F2分别是焦点, ①如果∠F1PF2=60o,求ΔF1PF2的周长及面积;②|PF1|?|PF2|的最大值。 P⑺已知点P为椭圆x2/25+y2/9=1上的一点,F1、F2为椭圆的左焦点与右焦点,点P到左准线的距离为d1, 点P到右准线的距离为d2。
①若|PF1|=4,则d2=______;
②若|PF1|∶|PF2|=2∶3,则点P的坐标是_______;
③若d2=4.5,则d1=_______;
④若P(3,y),则|PF1|=______;
⑤若|PF1|⊥|PF2|,则点P的坐标是_____;⑥若点M(3,-2)在椭圆内部,则|PM|+5|PF2|/4的最小值是_________。 15/2837/513/4⑻设椭圆x2/a2+y2/b2=1的两焦点为F1、F2,A1、A2为长轴的两个端点。
①P是椭圆上的一点,且∠F1PF2=60o,求ΔF1PF2的面积;
②若椭圆上存在一点Q,使∠A1QA2=120o,求椭圆离心率的范围。⑼求经过点M(1,2),以y轴为准线,离心率为1/2的椭圆左顶点的轨迹方程。⑴若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率是( )D2、利用图形及图形性质解题⑵已知椭圆 的一条准线方程是y=9/2,则m等于( ) A、1 B、2 C、3 D、7 A⑶椭圆两焦点和中心将两准线间的距离四等分,则一焦点与短轴连线的夹角是( )
A、45o B、60o C、90o D、120o
⑷椭圆x2/100+y2/36=1上的点P到它的左准线的距离是10,则点P到右焦点的距离是( )
A、15 B、12 C、10 D、8 CB⑸中心在原点,离心率为 ,且一条准线的方程是y=3的椭圆方程是______。
x2/2+y2/6=1
⑹点M与定点F(8,0)的距离和它到定直线 x=25/2的距离之比为4∶5,则点M的轨迹方程是_________。
x2/100+y2/36=1 总结归纳思想方法:坐标法、待定系数法、平方 法、数形结合
技巧:充分利用椭圆的定义解题
知识点:定义、标准方程、几何性质作业:P132 复习参考题八 5、6、8
3、进一步理解a、b、c、e的几何意义,会用几何性质解决有关问题
4、在坐标法的基础上掌握点的轨迹条件满足某曲线的定义时,用待定系数法求其方程1、椭圆的定义运用:
⑴ΔABC的周长为20,且B (-4,0),C(4,0),则点A的轨迹方程是_____________.
⑵已知A(-1,0),B(1,0),线段CA、AB、CB的长成等差数列,则点C的轨迹方程是_____________.
⑶过点A(0,2),且与圆B:x2+(y+2)2=36内切的动圆圆心C的轨迹方程是__________.x2/36+y2/20=1(y≠0)x2/4+y2/3=1x2/5+y2/9=1⑷一动圆C与圆A:(x+3)2+y2=1外切,与圆B:(x-3)2+y2=81内切,试求动圆圆心C的轨迹方程。
x2/25+y2/16=1
⑸椭圆x2/12+y2/3=1的一个左焦点为F1,点P在椭圆上,如果线段PF1的中点在y轴上,则点P的坐标是P⑹P是椭圆x2/100+y2/64=1上的一点,F1、F2分别是焦点, ①如果∠F1PF2=60o,求ΔF1PF2的周长及面积;②|PF1|?|PF2|的最大值。 P⑺已知点P为椭圆x2/25+y2/9=1上的一点,F1、F2为椭圆的左焦点与右焦点,点P到左准线的距离为d1, 点P到右准线的距离为d2。
①若|PF1|=4,则d2=______;
②若|PF1|∶|PF2|=2∶3,则点P的坐标是_______;
③若d2=4.5,则d1=_______;
④若P(3,y),则|PF1|=______;
⑤若|PF1|⊥|PF2|,则点P的坐标是_____;⑥若点M(3,-2)在椭圆内部,则|PM|+5|PF2|/4的最小值是_________。 15/2837/513/4⑻设椭圆x2/a2+y2/b2=1的两焦点为F1、F2,A1、A2为长轴的两个端点。
①P是椭圆上的一点,且∠F1PF2=60o,求ΔF1PF2的面积;
②若椭圆上存在一点Q,使∠A1QA2=120o,求椭圆离心率的范围。⑼求经过点M(1,2),以y轴为准线,离心率为1/2的椭圆左顶点的轨迹方程。⑴若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率是( )D2、利用图形及图形性质解题⑵已知椭圆 的一条准线方程是y=9/2,则m等于( ) A、1 B、2 C、3 D、7 A⑶椭圆两焦点和中心将两准线间的距离四等分,则一焦点与短轴连线的夹角是( )
A、45o B、60o C、90o D、120o
⑷椭圆x2/100+y2/36=1上的点P到它的左准线的距离是10,则点P到右焦点的距离是( )
A、15 B、12 C、10 D、8 CB⑸中心在原点,离心率为 ,且一条准线的方程是y=3的椭圆方程是______。
x2/2+y2/6=1
⑹点M与定点F(8,0)的距离和它到定直线 x=25/2的距离之比为4∶5,则点M的轨迹方程是_________。
x2/100+y2/36=1 总结归纳思想方法:坐标法、待定系数法、平方 法、数形结合
技巧:充分利用椭圆的定义解题
知识点:定义、标准方程、几何性质作业:P132 复习参考题八 5、6、8
