华师大版八年级数学下册第19章矩形、菱形与正方形 单元测试卷(word、含答案)
文档属性
| 名称 | 华师大版八年级数学下册第19章矩形、菱形与正方形 单元测试卷(word、含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 521.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 13:53:09 | ||
图片预览

文档简介
华师大版八年级数学下册单元测试卷
第19章矩形、菱形与正方形
时间:60分钟 总分:120分
一、选择题(每题3分,共24分)
1.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是 ( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量一组邻边是否相等 D.测量三个角是否为直角
2.正方形具有而矩形不一定具有的性质是 ( )
A.四个角都相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
3.如图,在正方形中有两个正方形,如果记正方形的面积为,正方形的面积为,则和的关系为 ( )
A. B. C. D.
4.下列关于矩形的说法不正确的是 ( )
A.对角线平分且相等 B.四个角都是直角
C.有四条对称轴 D.是中心对称图形
5.如图,要使平行四边形ABCD成为菱形,可添加的条件是 ( )
A. B. C. D.
6.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=12,BD=16,则菱形的高AE为 ( )
A.9.6 B.4.8 C.10 D.5
7.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则矩形ABCD的周长为 ( )
A.24 B.16 C.12 D.8
8.如图,正方形纸片ABCD的边长为15,E、F分别是CD、AD边上的点,连接AE,把正方形纸片沿BF折叠,使点A落在AE上的一点G,若CE=7,则GE的长为 ( )
A.3 B. C.4 D.
二、填空题(每题3分,共24分)
9.在菱形中,,,则菱形的边长等于______,
10.若一个正方形的一条对角线长为2,则它的周长为___________.
11.如图,在正方形ABCD内部作等边△CDE,连接BD.则的度数为______.
12.如图,矩形中,对角线交于点,如果,那么的度数为__________.
13.如图,平面内直线,且相邻两条平行线间隔均为1,正方形ABCD的4个顶点分别在4条平行线上,则正方形的面积为_________.
14.如图所示,菱形ABCD的对角线AC、BD相交于点若,,,垂足为E,则AE的长为______.
15.如图,在矩形ABCD中,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.若∠BDE=15°,则∠DOE=_____.
16.如图,已知:,,以AB为边作正方形ABCD,使P、D两点落在直线AB的两侧.当时,则PD的长为______.
三、解答题(每题9分,共72分)
17.已知:如图,在□中,点、分别在、上,且平分,//.求证:四边形是菱形.
18.如图,在菱形中,、分别为边和上的点,且.连接、交于点.求证:.
19.如图,已知平行四边形ABCD中,M,N是BD上的两点,且,.
(1)求证:四边形AMCN是矩形;
(2)若,,AB⊥AC,求四边形ABCD的面积.
20.如图,在矩形中,点,分别是,上的点,,且.求证:.
21.已知:如图,BE,BF分别是与它的邻补角的平分线,,垂足为点E,,垂足为点F,EF分别交边AB,AC于点M和N.
求证:
(1)四边形AFBE是矩形;
(2).
22.如图,将矩形ABCD绕着点B逆时针旋转得到矩形GBEF,使点C恰好落到线段AD上的E点处,连接CE,连接CG交BE于点H.
(1)求证:CE平分∠BED;
(2)取BC的中点M,连接MH,求证:MHBG;
(3)若BC=2AB=4,求CG的长.
23.在正方形ABCD中,点E是对角线AC上一点,点F是正方形ABCD外角平分线CM上一点,且CF=AE,连接BE,EF.
(1)如图1,当E是线段AC的中点时,BE与EF有何数量关系,并证明;
(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否仍然成立,并证明你的结论.
24.如图,四边形ABCD是菱形,点E,F在对角线AC上,且.
(1)求证:;
(2)求证:四边形DEBF是菱形.
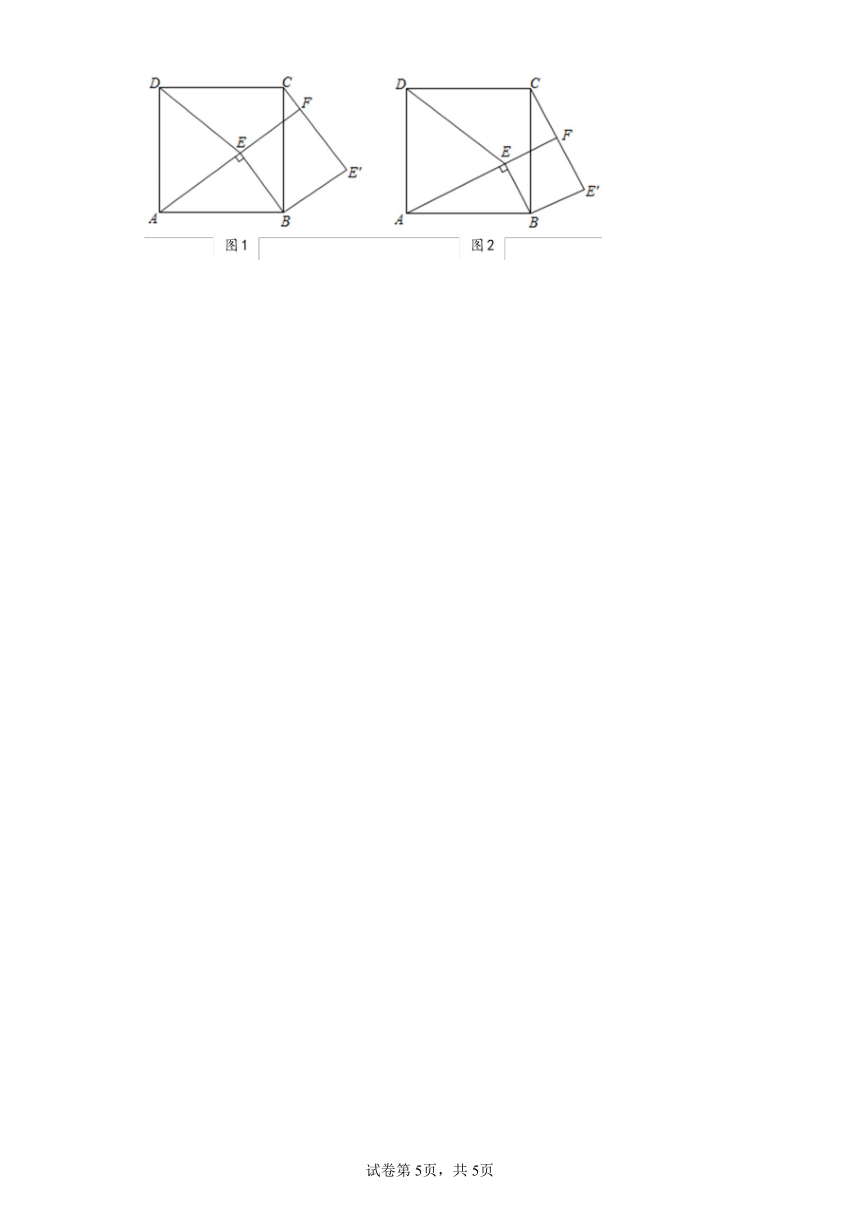
25.【问题情境】
如图1,点为正方形内一点,,将Rt△ABE绕点按顺时针方向旋转,得到(点的对应点为点.延长交于点,连接.
(1)试判断四边形的形状,并说明理由;
【解决问题】
(2)若请求出正方形的面积;
【猜想证明】
(3)如图2,若,请猜想线段与的数量关系并加以证明.
试卷第1页,共3页
试卷第1页,共5页
参考答案:
1.D
2.D
3.D
4.C
5.B
6.A
7.A
8.B
9.
10.
11.15°
12.
13.
14.
15.135°
16.
17.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF∥AB,
∴四边形ABFE是平行四边形,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠EBF,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
18.
证明:∵四边形ABCD是菱形,
∴DA=DC=AB=BC,
∵AE=CF,
∴DE=DF
在△DAF和△DCE中,
,
∴△DAF≌△DCE(SAS),
∴∠EAG=∠FCG,
在△AEG和△CFG中,
,
∴△AEG≌△CFG(AAS),
∴EG=FG,
在△DGE和△DGF中,
,
∴△DGE≌△DGF(SSS),
∴∠DGE=∠DGF.
19.
(1)证明:∵四边形ABCD是平行四边形,
∴,,
∵对角线BD上的两点M、N满足,
∴,即,
∴四边形AMCN是平行四边形,∴,
∵,∴,
∴四边形AMCN是矩形
(2)
∵四边形ABCD是平行四边形,
∴,,
∴,
∵,∴,
∵AB⊥AC,∴,
∴是等腰直角三角形,∴,
∴四边形ABCD的面积为.
20.
证明:∵矩形ABCD,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠CEF=90°,
∴∠AEF+∠CED=180°-∠CEF=90°,
∴∠AFE=∠CED,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS),
∴AF=DE.
21.
(1)证明:如图,
∵BE、BF分别是与的平分线,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴四边形AEBF为矩形.
(2)证明:∵四边形AEBF为矩形,
∴,
∴,
∵,
∴,
∴.
22.
(1)∵四边形ABCD是矩形,
∴BC=BE,DE∥BC,
∴∠BEC=∠BCE,∠BCE=∠DEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
(2)过点C作CN⊥BE,垂足为N,
∵四边形ABCD是矩形,
∴CD⊥DE,
∵CE平分∠BED,
∴CD=CN,
∵矩形ABCD绕着点B逆时针旋转得到矩形GBEF,
∴CD=BG,∠GBH=∠CNH=90°,
∴CN=BG,∠BHG=∠NHC,
∴△BHG≌△CHN,
∴HG=HC,
∴H是GC的中点,
∵BC的中点是M,
∴MH是△BGC中位线,
∴MHBG.
(3)过点C作CN⊥BE,垂足为N,
∵四边形ABCD是矩形,BC=2AB=4,矩形ABCD绕着点B逆时针旋转得到矩形GBEF,
∴GB⊥BH,GB=BM=2,
∵MH是△BGC中位线,
∴MH=1,
∴∠HBM=∠QGB,
∵GB=BM=2,∠BHM=∠GQB,
∴△QBG≌△HMB,
∴QB=MH=1,GQ=BH=,QC=5,
∴CG=.
23.
(1)解:(1)EF=BE
∵四边形ABCD是正方形
∴∠ABC=∠BCD=90°
∵点E是对角线AC中点
∴BE=AE=CE,∠CBE=∠BCE=∠ECD=45°
∵CM是正方形ABCD外角的平分线
∴∠DCF=45°
∴∠ECF=∠ECD+∠DCF=90°
∵CF=AE=CE=BE
∴EF2=CF2+CE2=2BE2
∴EF=BE
(2)EF=BE成立,证明如下:
如图1,过点B作BG⊥BE,交直线CM于点G,连接EG
∴∠EBG=∠ABC=90°
∴∠EBG-∠EBC=∠ABC-∠EBC
即∠CBG=∠ABE
∵∠ECF=45°+45°=90°,∠ECB=45°
∴∠ECG=90°,∠BCG=45°
在△CBG与△ABE中,
∴△CBG≌△ABE(ASA)
∴BG=BE,CG=AE
∴Rt△BEG中,EG2=BE2+BG2=2BE2
∵CF=AE
∴CF=CG
∴EC垂直平分FG
∴EF=EG
∴EF2=EG2=2BE2
∴EF=BE
24.
(1)证明:∵四边形ABCD是菱形,
∴,,
∴,
在和中,
∴;
(2)证明:由(1)得,
∴,,
∵,,
∴,
∴,
∴四边形DEBF是平行四边形,
∵四边形ABCD是菱形,
∴,
又∵,
∴,
∴,
∴四边形DEBF是菱形.
25.
(1)解:四边形是正方形,
证明:将绕点B按顺时针方向旋转90°,
∴,,,
又∵,
∴四边形是矩形,
又∵,
∴四边形是正方形;
(2)
解:∵,,
∴,
∵四边形是正方形,
∴,
∴,,
∴,
∴正方形ABCD的面积为225;
(3)
,理由如下:
如图,过点D作于H,
∵,,
∴,
∴,
∵四边形ABCD是正方形,
∴,,
∴,
∴,
又∵,,
∴(AAS),
∴,
∵将绕点B按顺时针方向旋转90°,
∴,
∵四边形是正方形,
∴,
∴.
答案第1页,共2页
答案第1页,共7页
第19章矩形、菱形与正方形
时间:60分钟 总分:120分
一、选择题(每题3分,共24分)
1.数学课上,老师要同学们判断一个四边形门框是否为矩形.下面是某合作小组的4位同学拟定的方案,其中正确的是 ( )
A.测量对角线是否互相平分 B.测量两组对边是否分别相等
C.测量一组邻边是否相等 D.测量三个角是否为直角
2.正方形具有而矩形不一定具有的性质是 ( )
A.四个角都相等 B.对角线互相平分
C.对角线相等 D.对角线互相垂直
3.如图,在正方形中有两个正方形,如果记正方形的面积为,正方形的面积为,则和的关系为 ( )
A. B. C. D.
4.下列关于矩形的说法不正确的是 ( )
A.对角线平分且相等 B.四个角都是直角
C.有四条对称轴 D.是中心对称图形
5.如图,要使平行四边形ABCD成为菱形,可添加的条件是 ( )
A. B. C. D.
6.如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=12,BD=16,则菱形的高AE为 ( )
A.9.6 B.4.8 C.10 D.5
7.如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC、AD于点E、F,若BE=3,AF=5,则矩形ABCD的周长为 ( )
A.24 B.16 C.12 D.8
8.如图,正方形纸片ABCD的边长为15,E、F分别是CD、AD边上的点,连接AE,把正方形纸片沿BF折叠,使点A落在AE上的一点G,若CE=7,则GE的长为 ( )
A.3 B. C.4 D.
二、填空题(每题3分,共24分)
9.在菱形中,,,则菱形的边长等于______,
10.若一个正方形的一条对角线长为2,则它的周长为___________.
11.如图,在正方形ABCD内部作等边△CDE,连接BD.则的度数为______.
12.如图,矩形中,对角线交于点,如果,那么的度数为__________.
13.如图,平面内直线,且相邻两条平行线间隔均为1,正方形ABCD的4个顶点分别在4条平行线上,则正方形的面积为_________.
14.如图所示,菱形ABCD的对角线AC、BD相交于点若,,,垂足为E,则AE的长为______.
15.如图,在矩形ABCD中,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.若∠BDE=15°,则∠DOE=_____.
16.如图,已知:,,以AB为边作正方形ABCD,使P、D两点落在直线AB的两侧.当时,则PD的长为______.
三、解答题(每题9分,共72分)
17.已知:如图,在□中,点、分别在、上,且平分,//.求证:四边形是菱形.
18.如图,在菱形中,、分别为边和上的点,且.连接、交于点.求证:.
19.如图,已知平行四边形ABCD中,M,N是BD上的两点,且,.
(1)求证:四边形AMCN是矩形;
(2)若,,AB⊥AC,求四边形ABCD的面积.
20.如图,在矩形中,点,分别是,上的点,,且.求证:.
21.已知:如图,BE,BF分别是与它的邻补角的平分线,,垂足为点E,,垂足为点F,EF分别交边AB,AC于点M和N.
求证:
(1)四边形AFBE是矩形;
(2).
22.如图,将矩形ABCD绕着点B逆时针旋转得到矩形GBEF,使点C恰好落到线段AD上的E点处,连接CE,连接CG交BE于点H.
(1)求证:CE平分∠BED;
(2)取BC的中点M,连接MH,求证:MHBG;
(3)若BC=2AB=4,求CG的长.
23.在正方形ABCD中,点E是对角线AC上一点,点F是正方形ABCD外角平分线CM上一点,且CF=AE,连接BE,EF.
(1)如图1,当E是线段AC的中点时,BE与EF有何数量关系,并证明;
(2)当点E不是线段AC的中点,其它条件不变时,请你在图2中补全图形,判断(1)中的结论是否仍然成立,并证明你的结论.
24.如图,四边形ABCD是菱形,点E,F在对角线AC上,且.
(1)求证:;
(2)求证:四边形DEBF是菱形.
25.【问题情境】
如图1,点为正方形内一点,,将Rt△ABE绕点按顺时针方向旋转,得到(点的对应点为点.延长交于点,连接.
(1)试判断四边形的形状,并说明理由;
【解决问题】
(2)若请求出正方形的面积;
【猜想证明】
(3)如图2,若,请猜想线段与的数量关系并加以证明.
试卷第1页,共3页
试卷第1页,共5页
参考答案:
1.D
2.D
3.D
4.C
5.B
6.A
7.A
8.B
9.
10.
11.15°
12.
13.
14.
15.135°
16.
17.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,
又∵EF∥AB,
∴四边形ABFE是平行四边形,
∵BE平分∠ABC,
∴∠ABE=∠FBE,
∵AD∥BC,
∴∠AEB=∠EBF,
∴∠ABE=∠AEB,
∴AB=AE,
∴平行四边形ABFE是菱形.
18.
证明:∵四边形ABCD是菱形,
∴DA=DC=AB=BC,
∵AE=CF,
∴DE=DF
在△DAF和△DCE中,
,
∴△DAF≌△DCE(SAS),
∴∠EAG=∠FCG,
在△AEG和△CFG中,
,
∴△AEG≌△CFG(AAS),
∴EG=FG,
在△DGE和△DGF中,
,
∴△DGE≌△DGF(SSS),
∴∠DGE=∠DGF.
19.
(1)证明:∵四边形ABCD是平行四边形,
∴,,
∵对角线BD上的两点M、N满足,
∴,即,
∴四边形AMCN是平行四边形,∴,
∵,∴,
∴四边形AMCN是矩形
(2)
∵四边形ABCD是平行四边形,
∴,,
∴,
∵,∴,
∵AB⊥AC,∴,
∴是等腰直角三角形,∴,
∴四边形ABCD的面积为.
20.
证明:∵矩形ABCD,
∴∠A=∠D=90°,
∴∠AEF+∠AFE=90°,
∵EF⊥EC,
∴∠CEF=90°,
∴∠AEF+∠CED=180°-∠CEF=90°,
∴∠AFE=∠CED,
在△AEF和△DCE中,
,
∴△AEF≌△DCE(AAS),
∴AF=DE.
21.
(1)证明:如图,
∵BE、BF分别是与的平分线,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴四边形AEBF为矩形.
(2)证明:∵四边形AEBF为矩形,
∴,
∴,
∵,
∴,
∴.
22.
(1)∵四边形ABCD是矩形,
∴BC=BE,DE∥BC,
∴∠BEC=∠BCE,∠BCE=∠DEC,
∴∠BEC=∠DEC,
∴CE平分∠BED.
(2)过点C作CN⊥BE,垂足为N,
∵四边形ABCD是矩形,
∴CD⊥DE,
∵CE平分∠BED,
∴CD=CN,
∵矩形ABCD绕着点B逆时针旋转得到矩形GBEF,
∴CD=BG,∠GBH=∠CNH=90°,
∴CN=BG,∠BHG=∠NHC,
∴△BHG≌△CHN,
∴HG=HC,
∴H是GC的中点,
∵BC的中点是M,
∴MH是△BGC中位线,
∴MHBG.
(3)过点C作CN⊥BE,垂足为N,
∵四边形ABCD是矩形,BC=2AB=4,矩形ABCD绕着点B逆时针旋转得到矩形GBEF,
∴GB⊥BH,GB=BM=2,
∵MH是△BGC中位线,
∴MH=1,
∴∠HBM=∠QGB,
∵GB=BM=2,∠BHM=∠GQB,
∴△QBG≌△HMB,
∴QB=MH=1,GQ=BH=,QC=5,
∴CG=.
23.
(1)解:(1)EF=BE
∵四边形ABCD是正方形
∴∠ABC=∠BCD=90°
∵点E是对角线AC中点
∴BE=AE=CE,∠CBE=∠BCE=∠ECD=45°
∵CM是正方形ABCD外角的平分线
∴∠DCF=45°
∴∠ECF=∠ECD+∠DCF=90°
∵CF=AE=CE=BE
∴EF2=CF2+CE2=2BE2
∴EF=BE
(2)EF=BE成立,证明如下:
如图1,过点B作BG⊥BE,交直线CM于点G,连接EG
∴∠EBG=∠ABC=90°
∴∠EBG-∠EBC=∠ABC-∠EBC
即∠CBG=∠ABE
∵∠ECF=45°+45°=90°,∠ECB=45°
∴∠ECG=90°,∠BCG=45°
在△CBG与△ABE中,
∴△CBG≌△ABE(ASA)
∴BG=BE,CG=AE
∴Rt△BEG中,EG2=BE2+BG2=2BE2
∵CF=AE
∴CF=CG
∴EC垂直平分FG
∴EF=EG
∴EF2=EG2=2BE2
∴EF=BE
24.
(1)证明:∵四边形ABCD是菱形,
∴,,
∴,
在和中,
∴;
(2)证明:由(1)得,
∴,,
∵,,
∴,
∴,
∴四边形DEBF是平行四边形,
∵四边形ABCD是菱形,
∴,
又∵,
∴,
∴,
∴四边形DEBF是菱形.
25.
(1)解:四边形是正方形,
证明:将绕点B按顺时针方向旋转90°,
∴,,,
又∵,
∴四边形是矩形,
又∵,
∴四边形是正方形;
(2)
解:∵,,
∴,
∵四边形是正方形,
∴,
∴,,
∴,
∴正方形ABCD的面积为225;
(3)
,理由如下:
如图,过点D作于H,
∵,,
∴,
∴,
∵四边形ABCD是正方形,
∴,,
∴,
∴,
又∵,,
∴(AAS),
∴,
∵将绕点B按顺时针方向旋转90°,
∴,
∵四边形是正方形,
∴,
∴.
答案第1页,共2页
答案第1页,共7页
