华师大版八年级数学下册 第20章数据的整理与初步处理 单元测试卷(word、含答案)
文档属性
| 名称 | 华师大版八年级数学下册 第20章数据的整理与初步处理 单元测试卷(word、含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 358.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览



文档简介
华师大版八年级数学下册单元测试卷
第20章数据的整理与初步处理
时间:60分钟 总分:120分
一、选择题(每题3分,共24分)
1.在学校举行的团体操比赛中,七位评委给某班的评分去掉一个最高分、一个最低分后得到五个有效评分,分别为:9.20,9.20,9.40,8.80,9.00(单位:分),这五个有效评分的平均数是 ( )
A.9.20 B.9.12 C.9.10 D.9.08
2.2022北京冬奥会期间,为了表达对志愿者工作的支持,某班学生积极参加捐款活动,该班50名学生的捐款统计情况如表:
金额/元 5 10 20 50 100
人数 6 17 14 8 5
则他们捐款金额的众数与中位数是 ( )
A.20 ,10 B.17,14 C.10,20 D.17,20
3.已知某位射击运动员10次射击成绩的平均数为8.5,中位数为8.6,众数为8,方差为0.18.如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是 ( )
A.平均数 B.中位数 C.众数 D.方差
4.某超市4月份新上架四种数量相同、款式不同的保温杯,该月这四款保温杯的销售量如表所示,则最适宜加大进货量的款式是 ( )
款式 甲 乙 丙 丁
销售量(个) 65 27 32 28
A.甲 B.乙 C.丙 D.丁
5.甲、乙两位学生各进行5次一分钟跳绳训练,经统计两人的平均成绩相同,方差分别为,,则成绩更为稳定的是 ( )
A.甲 B.乙 C.甲、乙成绩一样稳定 D.无法确定
6.某文具超市有A,B,C,D四种笔记本销售,它们的单价分别是5元,4元,3元,6元,某天的笔记本销售情况如图所示,那么这天该文具超市销售的笔记本的单价的平均值是 ( )
A.3元 B.4元 C.4.2元 D.4.5元
7.已知一样本数据4,4,5,6,m的中位数为4,则数m可能为( )
A.6 B.5 C.4.5 D.4
8.刘明明同学利用假期在小区义卖,他对某一周7天的收入数据进行分析,并列出方差公式:,则该组数据的众数是( )
A.7元 B.9元 C.10元 D.11元
二、填空题(每题3分,共24分)
9.数据:3、5、4、5、2、3的中位数是___________.
10.小红参加学校举办的“我爱我的祖国”主题演讲比赛,她的演讲内容、演讲能力、演讲效果得分分别为86分,72分,81分,若依次按照40%,30%,30%的百分比确定成绩,则她的平均成绩是__________分.
11.已知2、3、4、x1、x2、x3的平均数是5,则x1、x2、x3的平均数是__.
12.一组数据:1,3,4,3,5,2,这组数据的众数是____.
13.已知一组数据3,4,4,10,8,9,4,18,那么这组数据的极差是____.
14.初三某甲、乙两班举行一分钟跳绳比赛,他们每分钟跳绳次数的统计结果如表:
班级 参加人数 中位数 方差 平均数
甲 48 95 126 100
乙 48 102 164 100
根据图表中的信息,_______班的成绩波动更小,更稳定.
15.每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的读书册数,统计数据如表所示:
册数 0 1 2 3 4
人数 3 13 16 17 1
在这组数据中,这50名学生读书册数的众数记为m、中位数记为n,则m+n=______.
16.一组数据由5个数组成,其中4个数分别为2,3,4,5且这组数据的平均数为4,则这组数据的方差为________.
三、解答题(每题9分,共72分)
17.某单位要招聘1名英语翻译,甲、乙两人报名参加了4项素质测试,成绩如下(单位:分):
听 说 读 写
甲 90 80 85 78
乙 78 82 85 88
如果把听、说、读、写的成绩按3:3:2:2计算素质测试平均成绩,那么谁的平均成绩高?请说明理由.
18.今有两人跳高成绩按先后次序记录如下.
甲.1.9 1.6 1.7 1.6 1.2 1.7 1.7 1.9 1.8 1.9
乙.1.2 1.4 1.6 1.8 1.7 1.7 1.8 1.9 1.9 2.0
请你运用你学过的统计知识回答下列问题.
(1)请分别求出两组数据的平均数、众数和中位数;
(2)裁判根据他们的成绩最后评判甲获胜,你能说出裁判评判甲获胜的理由吗?
(3)教练根据他们的成绩最后选择乙去参加比赛,你能不能说出教练让乙去参加比赛的理由?
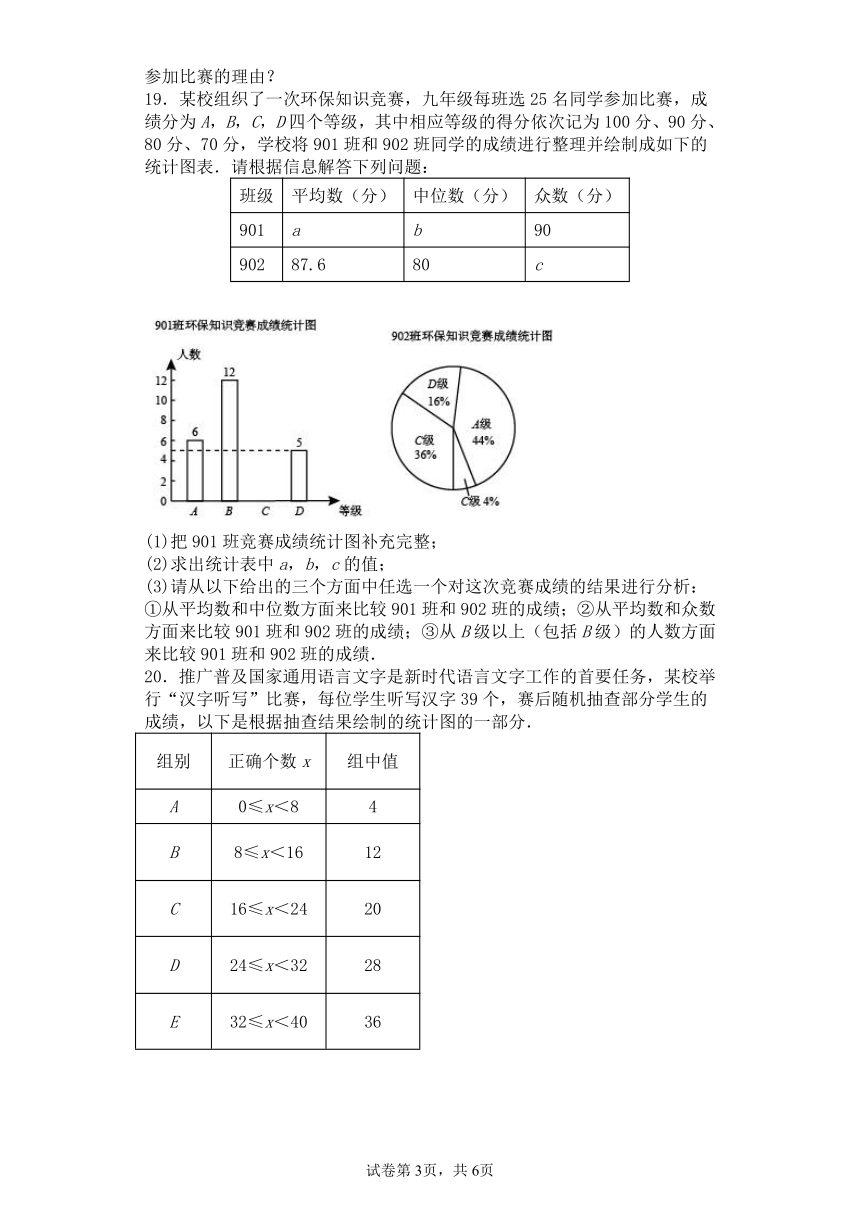
19.某校组织了一次环保知识竞赛,九年级每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将901班和902班同学的成绩进行整理并绘制成如下的统计图表.请根据信息解答下列问题:
班级 平均数(分) 中位数(分) 众数(分)
901 a b 90
902 87.6 80 c
(1)把901班竞赛成绩统计图补充完整;
(2)求出统计表中a,b,c的值;
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:①从平均数和中位数方面来比较901班和902班的成绩;②从平均数和众数方面来比较901班和902班的成绩;③从B级以上(包括B级)的人数方面来比较901班和902班的成绩.
20.推广普及国家通用语言文字是新时代语言文字工作的首要任务,某校举行“汉字听写”比赛,每位学生听写汉字39个,赛后随机抽查部分学生的成绩,以下是根据抽查结果绘制的统计图的一部分.
组别 正确个数x 组中值
A 0≤x<8 4
B 8≤x<16 12
C 16≤x<24 20
D 24≤x<32 28
E 32≤x<40 36
根据以上信息解决下列问题:
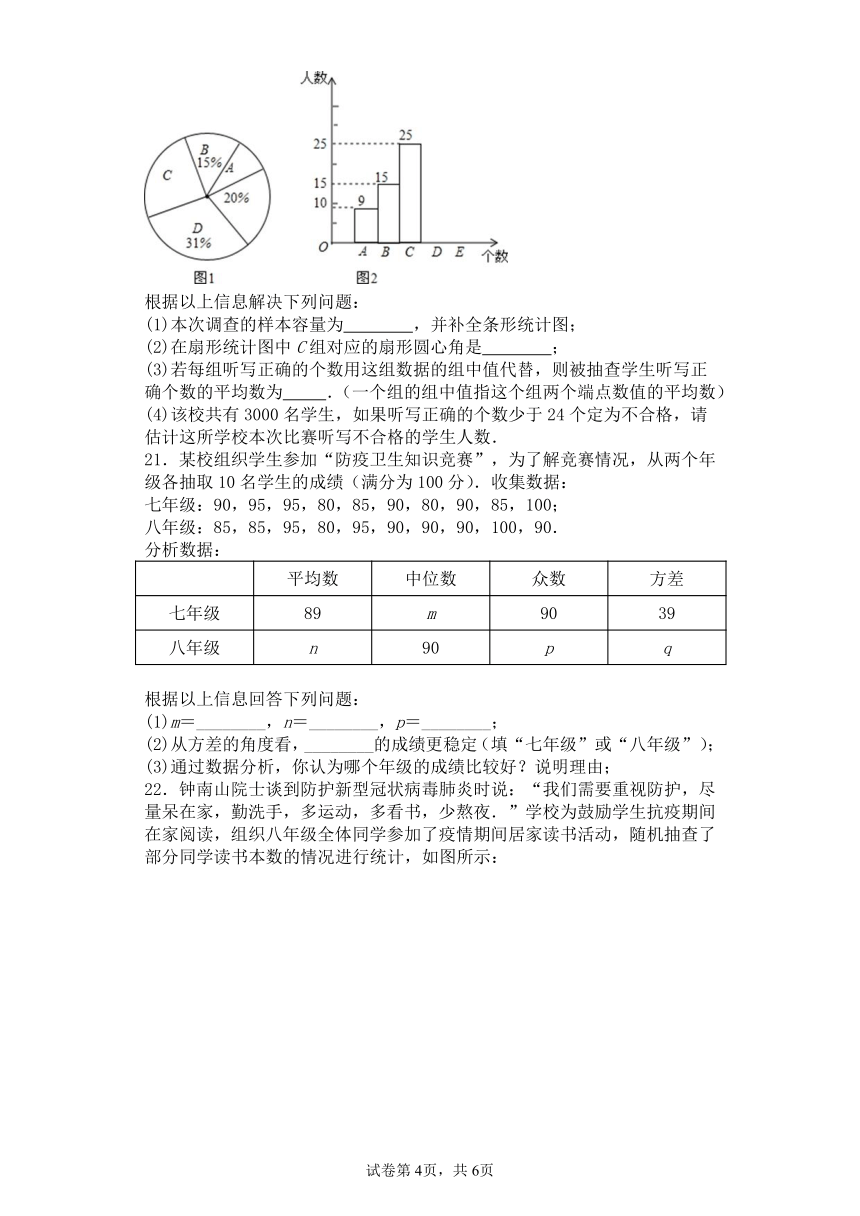
(1)本次调查的样本容量为 ,并补全条形统计图;
(2)在扇形统计图中C组对应的扇形圆心角是 ;
(3)若每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确个数的平均数为 .(一个组的组中值指这个组两个端点数值的平均数)
(4)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请估计这所学校本次比赛听写不合格的学生人数.
21.某校组织学生参加“防疫卫生知识竞赛”,为了解竞赛情况,从两个年级各抽取10名学生的成绩(满分为100分).收集数据:
七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
分析数据:
平均数 中位数 众数 方差
七年级 89 m 90 39
八年级 n 90 p q
根据以上信息回答下列问题:
(1)m=________,n=________,p=________;
(2)从方差的角度看,________的成绩更稳定(填“七年级”或“八年级”);
(3)通过数据分析,你认为哪个年级的成绩比较好?说明理由;
22.钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,尽量呆在家,勤洗手,多运动,多看书,少熬夜.”学校为鼓励学生抗疫期间在家阅读,组织八年级全体同学参加了疫情期间居家读书活动,随机抽查了部分同学读书本数的情况进行统计,如图所示:
(1)本次共抽查学生______人,并将条形统计图补充完整;
(2)读书本数的众数是______本,中位数是_______本;
(3)在八年级2000名学生中,读书15本及以上(含15本)的学生估计有多少人?
23.小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如图测试成绩折线统计图.根据图中信息,解答下列问题:
(1)求出两位同学的平均成绩;
(2)求出两位同学共12次成绩的中位数和众数;
(3)求出小聪成绩的方差.
24.为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
(1)校团委随机调查了 名学生.
(2)被调查的部分学生一周零花钱的平均数是 元,中位数是 元.
(3)“50元”所在扇形的圆心角的度数为 .
(4)为捐助贫困山区希望小学,全校1000名学生每人自发地捐出一周零花钱,请估算全校学生共捐款多少元?
25.甲、乙两名队员参加射击训练,每次射击的环数均为整数.其成绩分别被制成如下统计图表(乙队员射击训练成绩统计图部分被污染):
平均成绩/环 中位数/环 众数/环 方差/环2
甲 7 7 12
乙 7 8
根据以上信息,解决下列问题:
(1)求出的值;
(2)直接写出乙队员第7次的射击环数及的值,并求出的值;
(3)若要选派其中一名参赛,你认为应选哪名队员?请说明你的理由.
试卷第1页,共3页
试卷第1页,共6页
参考答案:
1.B
2.C
3.B
4.A
5.B
6.C
7.D
8.C
9.3.5
10.80.3
11.7
12.3
13.15
14.甲
15.5
16.2
17.
解:甲的平均成绩高,
∵甲的平均成绩:(分),
乙的平均成绩:(分),
,
∴甲的平均成绩高.
18.
(1)解:甲的平均成绩:×(1.9×3+1.8+1.7×3+1.6×2+1.2)=1.7,
乙的平均成绩:×(2.0+1.9×2+1.8×2+1.7×2+1.6+1.4+1.2)=1.7;
甲:1.7,1.9分别出现3次,最多,
∴众数是1.7和1.9,第5、6个两个数的平均数是(1.7+1.7)÷2=1.7,
∴中位数是1.7,
乙:1.7,1.8,1.9分别出现2次,最多,
∴众数是1.7,1.8,1.9,第5、6个两个数的平均数是(1.7+1.8)÷2=1.75,
∴中位数是1.75.
(2)
=(3×0.22+3×0.12+0.52)=0.04;
=(2×0.32+2×0.22+3×0.12+0.52)=0.054;
∵<,
∴甲更稳定;裁判评判甲获胜.
(3)选择乙去参加比赛,因为乙的成绩在逐步提高,而且最后成绩高于甲.
19.
(1)解:C等级的人数为25-6-12-5=2(人)
(2)根据题意得:901班的平均分为(分),
901班的成绩按从小到大顺序排列,处在第13位的是B级即90分,故中位数为90分;
902班占比最多的是A级44%,故902班的众数为100分,
则a=87.6,b=90,c=100.
(3)用②来进行分析,901班与902班的平均数相同,但是902班众数为100分,901班的众数为90分,则902班成绩较好.
20.
(1)解:抽取的学生总数是:15÷15%=100(人),
D组的人数是100×31%=31(人),
E组的人数是:100×20%=20(人).
故答案为:100;
(2)解:C组所占百分比为,扇形统计图中C组对应的扇形圆心角是,
故答案为:90°;
(3)解:被抽查学生听写正确个数的平均数为;
(4)解:这所学校本次比赛听写不合格的学生人数是:30001470(人)
估计这所学校本次比赛听写不合格的学生人数1470人.
21.
(1)解:七年级的中位数为=90分,故m=90;
八年级的平均数为:110×(85+85+95+80+95+90+90+90+100+90]=90,故n=90;
八年级中90分的最多,故p=90;
故答案为:90,90,90.
(2)解:八年级的方差;
∴八年级的成绩更稳定,
故答案为:八年级.
(3)解:八年级成绩更好.理由是:
七、八年级学生成绩的中位数和众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更稳定,
综上,八年级的学生成绩好.
22.
(1)解:由统计图可得,本次共抽查学生:(人),
读10本书的人数为:50-9-14-7-4=16(人)
补全条形统计图如下:
(2)解:由条形统计图可知,读书本数10本的人数最多,
∴读书本数的众数是10本;
把上述数据按照从小到大的顺序排列处于中间的是10本和15本,
∴中位数是(本).
(3)解:(人)
答:在八年级2000名学生中,读书15本及以上(含15本)的学生估计有1000人.
23.
(1)解:小聪的平均成绩:(分),
小明的平均成绩:(分),
∴两位同学的平均成绩分别是:8分和8分;
(2)解:两位同学共12次成绩按大小顺序:6,6,7,7,7,7,8,9,9,10,10,10
∴中位数,
∵出现次数最多的数是7,
∴众数为:7;
(3)解:小聪成绩的方差: .
24.
解;
(1)校团委随机调查的学生有:10 ÷25%= 40(人),
故答案为: 40;
(2)零花钱有20元的学生有: 40×15%= 6(人)
被调查的部分学生一周零花钱的平均数是:
× (20×6+30×18+ 40×10+ 50×4) = 31.5(元)
把这些数从小到大排列,中位数是第20、21个数的平均数,则中位数是 = 30,
故答案为: 31.5, 30;
(3)表示“50元”的扇形的圆心角度数是:
360°×=36°
故答案为: 36°;
(4)全校学生共捐款约为:
1000 × 31.5 = 3150(元).
25.
解:(1)甲的平均成绩a=(环);
(2)∵已知的环数分别是: 3、4、6、7、8、8、9、10,平均数是7,
可知剩余两次的成绩和为:70-55=15(环),根据统计图可知不可能是9和6,只能是7和8,所以乙队员第7次的射击环数是7环或8环;
把乙的成绩从小到大排列:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
其方差c=×[(3﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+3×(8﹣7)2+(9﹣7)2+(10﹣7)2]
=×(16+9+1+3+4+9)
=4.2;
(3)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看乙的成绩比甲的成绩稳定;综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
第20章数据的整理与初步处理
时间:60分钟 总分:120分
一、选择题(每题3分,共24分)
1.在学校举行的团体操比赛中,七位评委给某班的评分去掉一个最高分、一个最低分后得到五个有效评分,分别为:9.20,9.20,9.40,8.80,9.00(单位:分),这五个有效评分的平均数是 ( )
A.9.20 B.9.12 C.9.10 D.9.08
2.2022北京冬奥会期间,为了表达对志愿者工作的支持,某班学生积极参加捐款活动,该班50名学生的捐款统计情况如表:
金额/元 5 10 20 50 100
人数 6 17 14 8 5
则他们捐款金额的众数与中位数是 ( )
A.20 ,10 B.17,14 C.10,20 D.17,20
3.已知某位射击运动员10次射击成绩的平均数为8.5,中位数为8.6,众数为8,方差为0.18.如果去掉一个最高分和一个最低分,则下列数据一定不发生变化的是 ( )
A.平均数 B.中位数 C.众数 D.方差
4.某超市4月份新上架四种数量相同、款式不同的保温杯,该月这四款保温杯的销售量如表所示,则最适宜加大进货量的款式是 ( )
款式 甲 乙 丙 丁
销售量(个) 65 27 32 28
A.甲 B.乙 C.丙 D.丁
5.甲、乙两位学生各进行5次一分钟跳绳训练,经统计两人的平均成绩相同,方差分别为,,则成绩更为稳定的是 ( )
A.甲 B.乙 C.甲、乙成绩一样稳定 D.无法确定
6.某文具超市有A,B,C,D四种笔记本销售,它们的单价分别是5元,4元,3元,6元,某天的笔记本销售情况如图所示,那么这天该文具超市销售的笔记本的单价的平均值是 ( )
A.3元 B.4元 C.4.2元 D.4.5元
7.已知一样本数据4,4,5,6,m的中位数为4,则数m可能为( )
A.6 B.5 C.4.5 D.4
8.刘明明同学利用假期在小区义卖,他对某一周7天的收入数据进行分析,并列出方差公式:,则该组数据的众数是( )
A.7元 B.9元 C.10元 D.11元
二、填空题(每题3分,共24分)
9.数据:3、5、4、5、2、3的中位数是___________.
10.小红参加学校举办的“我爱我的祖国”主题演讲比赛,她的演讲内容、演讲能力、演讲效果得分分别为86分,72分,81分,若依次按照40%,30%,30%的百分比确定成绩,则她的平均成绩是__________分.
11.已知2、3、4、x1、x2、x3的平均数是5,则x1、x2、x3的平均数是__.
12.一组数据:1,3,4,3,5,2,这组数据的众数是____.
13.已知一组数据3,4,4,10,8,9,4,18,那么这组数据的极差是____.
14.初三某甲、乙两班举行一分钟跳绳比赛,他们每分钟跳绳次数的统计结果如表:
班级 参加人数 中位数 方差 平均数
甲 48 95 126 100
乙 48 102 164 100
根据图表中的信息,_______班的成绩波动更小,更稳定.
15.每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的读书册数,统计数据如表所示:
册数 0 1 2 3 4
人数 3 13 16 17 1
在这组数据中,这50名学生读书册数的众数记为m、中位数记为n,则m+n=______.
16.一组数据由5个数组成,其中4个数分别为2,3,4,5且这组数据的平均数为4,则这组数据的方差为________.
三、解答题(每题9分,共72分)
17.某单位要招聘1名英语翻译,甲、乙两人报名参加了4项素质测试,成绩如下(单位:分):
听 说 读 写
甲 90 80 85 78
乙 78 82 85 88
如果把听、说、读、写的成绩按3:3:2:2计算素质测试平均成绩,那么谁的平均成绩高?请说明理由.
18.今有两人跳高成绩按先后次序记录如下.
甲.1.9 1.6 1.7 1.6 1.2 1.7 1.7 1.9 1.8 1.9
乙.1.2 1.4 1.6 1.8 1.7 1.7 1.8 1.9 1.9 2.0
请你运用你学过的统计知识回答下列问题.
(1)请分别求出两组数据的平均数、众数和中位数;
(2)裁判根据他们的成绩最后评判甲获胜,你能说出裁判评判甲获胜的理由吗?
(3)教练根据他们的成绩最后选择乙去参加比赛,你能不能说出教练让乙去参加比赛的理由?
19.某校组织了一次环保知识竞赛,九年级每班选25名同学参加比赛,成绩分为A,B,C,D四个等级,其中相应等级的得分依次记为100分、90分、80分、70分,学校将901班和902班同学的成绩进行整理并绘制成如下的统计图表.请根据信息解答下列问题:
班级 平均数(分) 中位数(分) 众数(分)
901 a b 90
902 87.6 80 c
(1)把901班竞赛成绩统计图补充完整;
(2)求出统计表中a,b,c的值;
(3)请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析:①从平均数和中位数方面来比较901班和902班的成绩;②从平均数和众数方面来比较901班和902班的成绩;③从B级以上(包括B级)的人数方面来比较901班和902班的成绩.
20.推广普及国家通用语言文字是新时代语言文字工作的首要任务,某校举行“汉字听写”比赛,每位学生听写汉字39个,赛后随机抽查部分学生的成绩,以下是根据抽查结果绘制的统计图的一部分.
组别 正确个数x 组中值
A 0≤x<8 4
B 8≤x<16 12
C 16≤x<24 20
D 24≤x<32 28
E 32≤x<40 36
根据以上信息解决下列问题:
(1)本次调查的样本容量为 ,并补全条形统计图;
(2)在扇形统计图中C组对应的扇形圆心角是 ;
(3)若每组听写正确的个数用这组数据的组中值代替,则被抽查学生听写正确个数的平均数为 .(一个组的组中值指这个组两个端点数值的平均数)
(4)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请估计这所学校本次比赛听写不合格的学生人数.
21.某校组织学生参加“防疫卫生知识竞赛”,为了解竞赛情况,从两个年级各抽取10名学生的成绩(满分为100分).收集数据:
七年级:90,95,95,80,85,90,80,90,85,100;
八年级:85,85,95,80,95,90,90,90,100,90.
分析数据:
平均数 中位数 众数 方差
七年级 89 m 90 39
八年级 n 90 p q
根据以上信息回答下列问题:
(1)m=________,n=________,p=________;
(2)从方差的角度看,________的成绩更稳定(填“七年级”或“八年级”);
(3)通过数据分析,你认为哪个年级的成绩比较好?说明理由;
22.钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,尽量呆在家,勤洗手,多运动,多看书,少熬夜.”学校为鼓励学生抗疫期间在家阅读,组织八年级全体同学参加了疫情期间居家读书活动,随机抽查了部分同学读书本数的情况进行统计,如图所示:
(1)本次共抽查学生______人,并将条形统计图补充完整;
(2)读书本数的众数是______本,中位数是_______本;
(3)在八年级2000名学生中,读书15本及以上(含15本)的学生估计有多少人?
23.小聪、小明准备代表班级参加学校“党史知识”竞赛,班主任对这两名同学测试了6次,获得如图测试成绩折线统计图.根据图中信息,解答下列问题:
(1)求出两位同学的平均成绩;
(2)求出两位同学共12次成绩的中位数和众数;
(3)求出小聪成绩的方差.
24.为了解学生零花钱的使用情况,校团委随机调查了本校部分学生每人一周的零花钱数额,并绘制了如图所示的两个统计图(部分未完成).请根据图中信息,回答下列问题:
(1)校团委随机调查了 名学生.
(2)被调查的部分学生一周零花钱的平均数是 元,中位数是 元.
(3)“50元”所在扇形的圆心角的度数为 .
(4)为捐助贫困山区希望小学,全校1000名学生每人自发地捐出一周零花钱,请估算全校学生共捐款多少元?
25.甲、乙两名队员参加射击训练,每次射击的环数均为整数.其成绩分别被制成如下统计图表(乙队员射击训练成绩统计图部分被污染):
平均成绩/环 中位数/环 众数/环 方差/环2
甲 7 7 12
乙 7 8
根据以上信息,解决下列问题:
(1)求出的值;
(2)直接写出乙队员第7次的射击环数及的值,并求出的值;
(3)若要选派其中一名参赛,你认为应选哪名队员?请说明你的理由.
试卷第1页,共3页
试卷第1页,共6页
参考答案:
1.B
2.C
3.B
4.A
5.B
6.C
7.D
8.C
9.3.5
10.80.3
11.7
12.3
13.15
14.甲
15.5
16.2
17.
解:甲的平均成绩高,
∵甲的平均成绩:(分),
乙的平均成绩:(分),
,
∴甲的平均成绩高.
18.
(1)解:甲的平均成绩:×(1.9×3+1.8+1.7×3+1.6×2+1.2)=1.7,
乙的平均成绩:×(2.0+1.9×2+1.8×2+1.7×2+1.6+1.4+1.2)=1.7;
甲:1.7,1.9分别出现3次,最多,
∴众数是1.7和1.9,第5、6个两个数的平均数是(1.7+1.7)÷2=1.7,
∴中位数是1.7,
乙:1.7,1.8,1.9分别出现2次,最多,
∴众数是1.7,1.8,1.9,第5、6个两个数的平均数是(1.7+1.8)÷2=1.75,
∴中位数是1.75.
(2)
=(3×0.22+3×0.12+0.52)=0.04;
=(2×0.32+2×0.22+3×0.12+0.52)=0.054;
∵<,
∴甲更稳定;裁判评判甲获胜.
(3)选择乙去参加比赛,因为乙的成绩在逐步提高,而且最后成绩高于甲.
19.
(1)解:C等级的人数为25-6-12-5=2(人)
(2)根据题意得:901班的平均分为(分),
901班的成绩按从小到大顺序排列,处在第13位的是B级即90分,故中位数为90分;
902班占比最多的是A级44%,故902班的众数为100分,
则a=87.6,b=90,c=100.
(3)用②来进行分析,901班与902班的平均数相同,但是902班众数为100分,901班的众数为90分,则902班成绩较好.
20.
(1)解:抽取的学生总数是:15÷15%=100(人),
D组的人数是100×31%=31(人),
E组的人数是:100×20%=20(人).
故答案为:100;
(2)解:C组所占百分比为,扇形统计图中C组对应的扇形圆心角是,
故答案为:90°;
(3)解:被抽查学生听写正确个数的平均数为;
(4)解:这所学校本次比赛听写不合格的学生人数是:30001470(人)
估计这所学校本次比赛听写不合格的学生人数1470人.
21.
(1)解:七年级的中位数为=90分,故m=90;
八年级的平均数为:110×(85+85+95+80+95+90+90+90+100+90]=90,故n=90;
八年级中90分的最多,故p=90;
故答案为:90,90,90.
(2)解:八年级的方差;
∴八年级的成绩更稳定,
故答案为:八年级.
(3)解:八年级成绩更好.理由是:
七、八年级学生成绩的中位数和众数相同,但八年级的平均成绩比七年级高,且从方差看,八年级学生成绩更稳定,
综上,八年级的学生成绩好.
22.
(1)解:由统计图可得,本次共抽查学生:(人),
读10本书的人数为:50-9-14-7-4=16(人)
补全条形统计图如下:
(2)解:由条形统计图可知,读书本数10本的人数最多,
∴读书本数的众数是10本;
把上述数据按照从小到大的顺序排列处于中间的是10本和15本,
∴中位数是(本).
(3)解:(人)
答:在八年级2000名学生中,读书15本及以上(含15本)的学生估计有1000人.
23.
(1)解:小聪的平均成绩:(分),
小明的平均成绩:(分),
∴两位同学的平均成绩分别是:8分和8分;
(2)解:两位同学共12次成绩按大小顺序:6,6,7,7,7,7,8,9,9,10,10,10
∴中位数,
∵出现次数最多的数是7,
∴众数为:7;
(3)解:小聪成绩的方差: .
24.
解;
(1)校团委随机调查的学生有:10 ÷25%= 40(人),
故答案为: 40;
(2)零花钱有20元的学生有: 40×15%= 6(人)
被调查的部分学生一周零花钱的平均数是:
× (20×6+30×18+ 40×10+ 50×4) = 31.5(元)
把这些数从小到大排列,中位数是第20、21个数的平均数,则中位数是 = 30,
故答案为: 31.5, 30;
(3)表示“50元”的扇形的圆心角度数是:
360°×=36°
故答案为: 36°;
(4)全校学生共捐款约为:
1000 × 31.5 = 3150(元).
25.
解:(1)甲的平均成绩a=(环);
(2)∵已知的环数分别是: 3、4、6、7、8、8、9、10,平均数是7,
可知剩余两次的成绩和为:70-55=15(环),根据统计图可知不可能是9和6,只能是7和8,所以乙队员第7次的射击环数是7环或8环;
把乙的成绩从小到大排列:3、4、6、7、7、8、8、8、9、10,
∴乙射击成绩的中位数b==7.5(环),
其方差c=×[(3﹣7)2+(4﹣7)2+(6﹣7)2+2×(7﹣7)2+3×(8﹣7)2+(9﹣7)2+(10﹣7)2]
=×(16+9+1+3+4+9)
=4.2;
(3)从平均成绩看甲、乙二人的成绩相等均为7环,从中位数看甲射中7环以上的次数小于乙,从众数看甲射中7环的次数最多而乙射中8环的次数最多,从方差看乙的成绩比甲的成绩稳定;综合以上各因素,若选派一名队员参加比赛的话,可选择乙参赛,因为乙获得高分的可能更大.
