双曲线及其标准方程第二课时[上学期]
文档属性
| 名称 | 双曲线及其标准方程第二课时[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 695.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-08 00:00:00 | ||
图片预览






文档简介
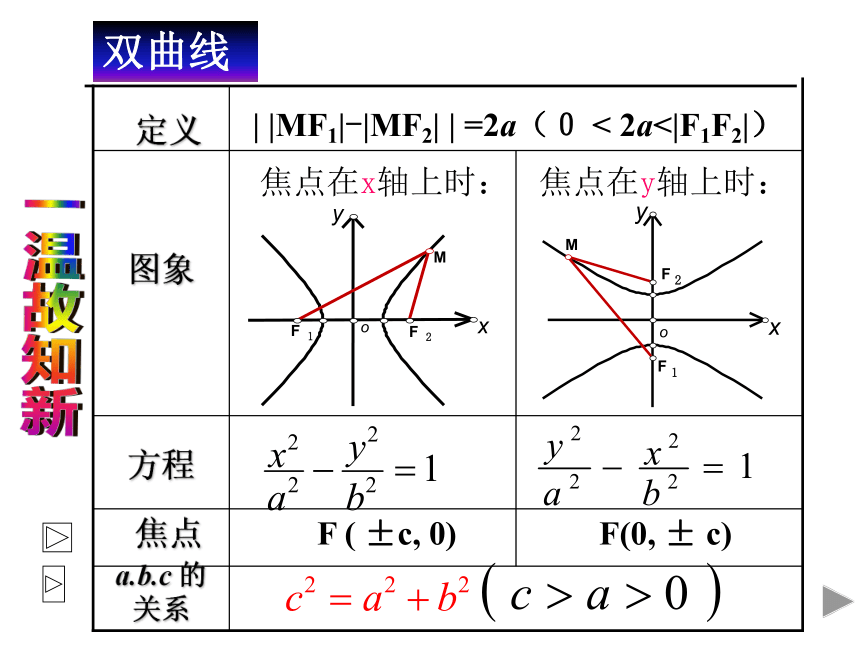
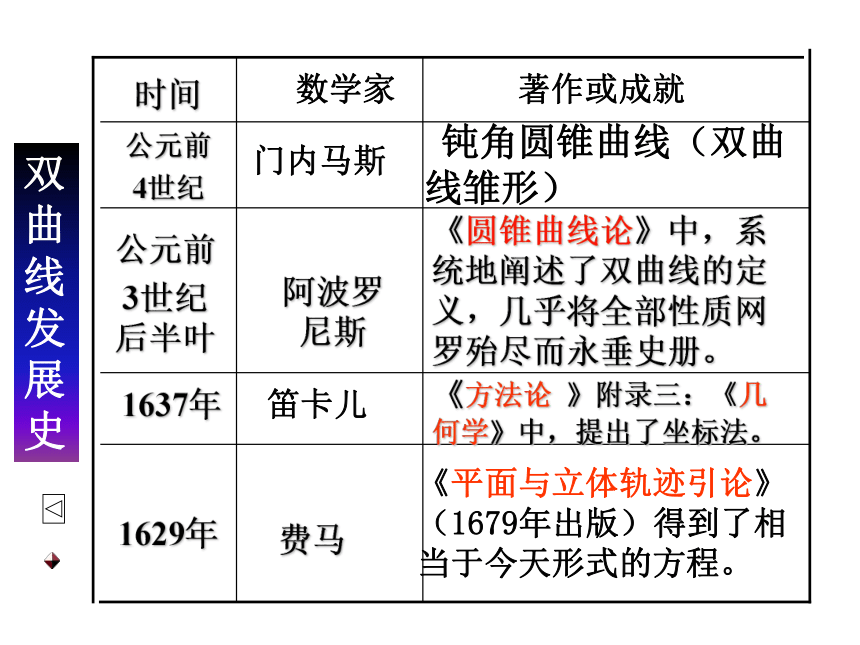
课件25张PPT。(第二课时)双曲线及其标准方程 方程焦点a.b.c 的关系图象定义| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)F ( ±c, 0) F(0, ± c)yxoF2F1MxyF2F1M焦点在x轴上时:焦点在y轴上时:一温故知新双曲线o时间数学家双曲线发展史著作或成就 ①、②两题的解法分别是什么? 引例:求适合下列条件的双曲线的标准方程
=3,b=4;
② = ,经过点A ,焦点在x轴上。 答案: ①定义法②待定系数法一温故知新二、新知探索、掌握算法例1(课本106页例2) :已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的
坐标分别为 , ,求双曲线的标准方程.已知双曲线经过两点,求双曲线标准方程,
用什么办法解决呢? 分析:由于焦点在y轴上,所以双曲线的标准方程可直接设出来,进行求解 。因为 在双曲线上,所以点 、 的坐标适合方程,将它们的坐标分别代入方
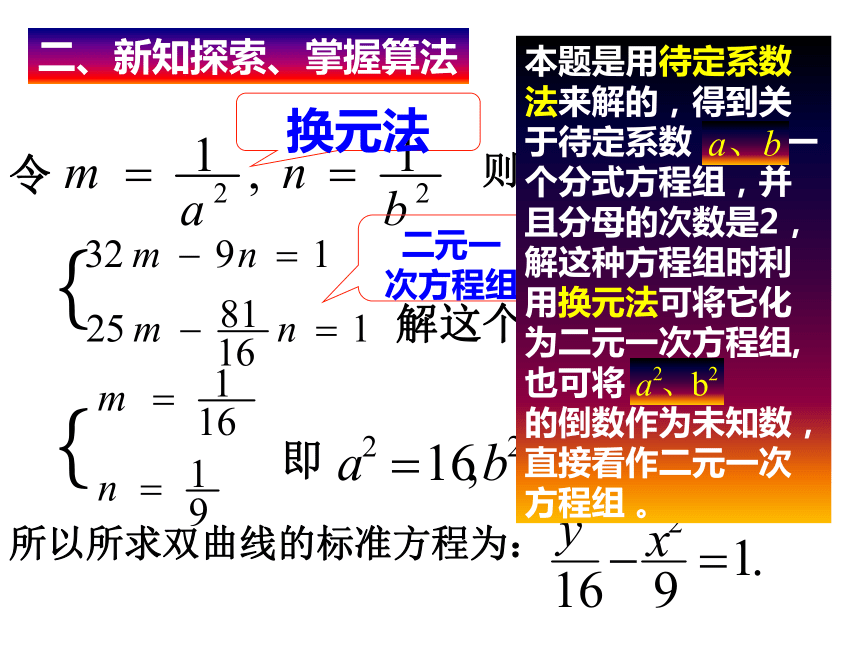
程中得到方程组 思考:这个方程组有何特点?解:∵双曲线的焦点在 y轴, ∴设所求双曲线的标准方程为:{二、新知探索、掌握算法问题的解答分母是二次的分式方程组。{{则方程组化为: 解这个方程组得:所以所求双曲线的标准方程为:令即二、新知探索、掌握算法换元法二元一
次方程组本题是用待定系数法来解的,得到关于待定系数 的一个分式方程组,并且分母的次数是2,解这种方程组时利用换元法可将它化为二元一次方程组,也可将 的倒数作为未知数,直接看作二元一次方程组 。 答案: 三、练习巩固例1(课本106页例2) :已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的坐标分别为 , ,求双曲线的标准方程.1.例1(变题)已知双曲线上两点 , 的坐标分别为 , ,
求双曲线的标准方程. 答案:所求的双曲线方程仍为将双曲线方程设为 求出 A 、B既避免了讨论,又降低了方程组、未知数的次数,大大减少所需的运算。例1.已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的坐标分为 , ,求双曲线的标准方程.例1(变题)已知双曲线上两点 , 的坐标分别为 , ,
求双曲线的标准方程.二、变式计算、发散思维分焦点在X轴上、y轴上两类情况讨论焦点在 y轴上,双曲线方程为若焦点在 X轴上,设所求双曲线方程为 依题意得:{此时无解。故所求的双曲线方程仍为 不讲一般式,直接练习例1.已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的坐标分为 , ,求双曲线的标准方程.例1(变题)已知双曲线上两点 , 的坐标分别为 , ,
求双曲线的标准方程.二、变式计算、发散思维分焦点在X轴上、y轴上两类情况讨论焦点在 y轴上,双曲线方程为若焦点在 X轴上,设所求双曲线方程为 依题意得:{此时无解。故所求的双曲线方程仍为 若去掉“焦点在y轴上”这一条件,
解这道题能不能不讨论呢?不讲一般式,直接练习例1(变题)已知双曲线上两点 ,
的坐标分别为 , ,
求双曲线的标准方程.
分析:能,设所求双曲线方程为: 依题意得:{解得{故所求双曲线标准方程为:
即
二、新知探索、掌握算法点评:当已知曲线上两点的坐标时,这样设所求双曲线方程不必讨论且解二元一次方程组简捷迅速,应予掌握.
BA例2 一炮弹在某处爆炸,在 A处听到的时 间比在 B处晚2S,(1)爆炸点应在什么样的曲线上?(2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程.分析:解应用题的关键是建 立 根据本题题设和结论,注意到在A处听到爆炸声的时间比B处 ,这里声速取定值. 数学模型晚2s四、联系实际,数学建模 P解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点 更远,所以爆炸点应在靠近 处的一支上.
离A处比离B处 B四、联系实际,数学建模 (2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程..设爆炸点P的坐标为 , 则 |PA|-|PB|= 340×2 =680 ,即 2 =680, =340.o (2)如图:建立直角坐标系,使A、B两点在轴 上,并且点O与线段AB的中点重合.又|AB|=800,∴2c=800,c=400, ∵|PA|-|PB|=680>0,∴ >0
所求双曲线的方程为:四、联系实际,数学建模 本题若|AB|=680m,曲线的方程是什么?A到B的距离恰好等于680米解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点离A处比离B处 更远,所以爆炸点应在靠近 B 处的一支上.解:(1) 若A、B两处距离差恰为2秒×声速,则爆炸点应在以B为端点的射线上.
故本题答案若为:爆炸点位于以A、B为焦点的双曲线靠近 B 处的一支上或在线段AB的延长线上,就更完美了。四、联系实际, 数学建模 A到B的距离恰好等于680米归纳应用:本例(2)利用两个不同的观测点得同一炮弹爆炸声的时间差,可以确定爆炸点所在的曲线的方程,但不能确定爆炸点的准确位置,如果再增设一个观测点C ,利用 A、C或(B、 C )两处测得的爆炸声的时间差,可以求出另一个曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.小 结:1、本课着重讲解了待定系数法求双曲线的标准方程,换元法解分母是二次的分式方程组,学习了双曲线的一个重要应用 。3、了解数学史可以提升自己的文化养。2、应注重方程思想和数形结合思想的数学功能,及基本元的方法。作业:一动点P(x,y)到两定点A(-1,0),B(1,0)的距离之差的绝对值为定值a,求P点轨迹方程,并说明曲线的形状. 1、阅读作业:查阅资料,进一步了解圆锥曲线发展史;
2、书面作业:课本P108习题8.3第3,6题;3、弹性作业:谢谢!温故知新若将常数改为大于|F1F2| ,则轨迹双曲线定义:平面内与两个定点F1,F2的距离的差的 等于正常数 的点的轨迹叫做双曲线。这两个定点F1,F2叫做双曲线的焦点,两焦点的距离| F1F2|叫做双曲线的焦距。若没有“绝对值”,则轨迹是双曲线的一支;以F1 ,F2 为端点的两条射线;不存在;若将常数改为等于|F1F2| ,则轨迹是若常数为0,则轨迹是线段F1F2的垂直平分线。数学探究绝对值 (小于|F1F2| )所求轨迹的方程为:例1. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.两条射线轨迹不存在上节课回顾线段F1F2的中垂线练习.一炮弹在某处爆炸,在 F1 (-5000,0)处听到爆炸声的时间比在F2(5000,0)处 晚 秒,已知坐标轴的单位长度为1米,声速为340米/秒,爆炸点应在什么样的曲线上?并求爆炸点所在的曲线方程.
同学们:让我们一起走进:“美妙的数学花园”感受数学文化吧! 是一切重大科学技术发展的基础,是理性文明的火车头。数学若去掉“焦点在y轴上”这一条件,
解这道题能不能不讨论呢?分焦点在X轴上、y轴上两类情况讨论若焦点在 X轴上,设所求双曲线方程为 依题意得:{此时无解。故所求的双曲线方程仍为 焦点在 y轴上,双曲线方程为
=3,b=4;
② = ,经过点A ,焦点在x轴上。 答案: ①定义法②待定系数法一温故知新二、新知探索、掌握算法例1(课本106页例2) :已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的
坐标分别为 , ,求双曲线的标准方程.已知双曲线经过两点,求双曲线标准方程,
用什么办法解决呢? 分析:由于焦点在y轴上,所以双曲线的标准方程可直接设出来,进行求解 。因为 在双曲线上,所以点 、 的坐标适合方程,将它们的坐标分别代入方
程中得到方程组 思考:这个方程组有何特点?解:∵双曲线的焦点在 y轴, ∴设所求双曲线的标准方程为:{二、新知探索、掌握算法问题的解答分母是二次的分式方程组。{{则方程组化为: 解这个方程组得:所以所求双曲线的标准方程为:令即二、新知探索、掌握算法换元法二元一
次方程组本题是用待定系数法来解的,得到关于待定系数 的一个分式方程组,并且分母的次数是2,解这种方程组时利用换元法可将它化为二元一次方程组,也可将 的倒数作为未知数,直接看作二元一次方程组 。 答案: 三、练习巩固例1(课本106页例2) :已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的坐标分别为 , ,求双曲线的标准方程.1.例1(变题)已知双曲线上两点 , 的坐标分别为 , ,
求双曲线的标准方程. 答案:所求的双曲线方程仍为将双曲线方程设为 求出 A 、B既避免了讨论,又降低了方程组、未知数的次数,大大减少所需的运算。例1.已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的坐标分为 , ,求双曲线的标准方程.例1(变题)已知双曲线上两点 , 的坐标分别为 , ,
求双曲线的标准方程.二、变式计算、发散思维分焦点在X轴上、y轴上两类情况讨论焦点在 y轴上,双曲线方程为若焦点在 X轴上,设所求双曲线方程为 依题意得:{此时无解。故所求的双曲线方程仍为 不讲一般式,直接练习例1.已知双曲线的焦点在y 轴上,并且双曲线上两点 、 的坐标分为 , ,求双曲线的标准方程.例1(变题)已知双曲线上两点 , 的坐标分别为 , ,
求双曲线的标准方程.二、变式计算、发散思维分焦点在X轴上、y轴上两类情况讨论焦点在 y轴上,双曲线方程为若焦点在 X轴上,设所求双曲线方程为 依题意得:{此时无解。故所求的双曲线方程仍为 若去掉“焦点在y轴上”这一条件,
解这道题能不能不讨论呢?不讲一般式,直接练习例1(变题)已知双曲线上两点 ,
的坐标分别为 , ,
求双曲线的标准方程.
分析:能,设所求双曲线方程为: 依题意得:{解得{故所求双曲线标准方程为:
即
二、新知探索、掌握算法点评:当已知曲线上两点的坐标时,这样设所求双曲线方程不必讨论且解二元一次方程组简捷迅速,应予掌握.
BA例2 一炮弹在某处爆炸,在 A处听到的时 间比在 B处晚2S,(1)爆炸点应在什么样的曲线上?(2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程.分析:解应用题的关键是建 立 根据本题题设和结论,注意到在A处听到爆炸声的时间比B处 ,这里声速取定值. 数学模型晚2s四、联系实际,数学建模 P解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点 更远,所以爆炸点应在靠近 处的一支上.
离A处比离B处 B四、联系实际,数学建模 (2)已知 A、B两地相距800m,并且此时声速为340m/s,求曲线的方程..设爆炸点P的坐标为 , 则 |PA|-|PB|= 340×2 =680 ,即 2 =680, =340.o (2)如图:建立直角坐标系,使A、B两点在轴 上,并且点O与线段AB的中点重合.又|AB|=800,∴2c=800,c=400, ∵|PA|-|PB|=680>0,∴ >0
所求双曲线的方程为:四、联系实际,数学建模 本题若|AB|=680m,曲线的方程是什么?A到B的距离恰好等于680米解:(1)由声速及A、B两处听到爆炸声的时间差,可知A、B两处与爆炸点的距离的差为定值,因此爆炸点应位于以A、B为焦点的双曲线上.因为爆炸点离A处比离B处 更远,所以爆炸点应在靠近 B 处的一支上.解:(1) 若A、B两处距离差恰为2秒×声速,则爆炸点应在以B为端点的射线上.
故本题答案若为:爆炸点位于以A、B为焦点的双曲线靠近 B 处的一支上或在线段AB的延长线上,就更完美了。四、联系实际, 数学建模 A到B的距离恰好等于680米归纳应用:本例(2)利用两个不同的观测点得同一炮弹爆炸声的时间差,可以确定爆炸点所在的曲线的方程,但不能确定爆炸点的准确位置,如果再增设一个观测点C ,利用 A、C或(B、 C )两处测得的爆炸声的时间差,可以求出另一个曲线的方程,解这两个方程组成的方程组,就能确定爆炸点的准确位置.这是双曲线的一个重要应用.小 结:1、本课着重讲解了待定系数法求双曲线的标准方程,换元法解分母是二次的分式方程组,学习了双曲线的一个重要应用 。3、了解数学史可以提升自己的文化养。2、应注重方程思想和数形结合思想的数学功能,及基本元的方法。作业:一动点P(x,y)到两定点A(-1,0),B(1,0)的距离之差的绝对值为定值a,求P点轨迹方程,并说明曲线的形状. 1、阅读作业:查阅资料,进一步了解圆锥曲线发展史;
2、书面作业:课本P108习题8.3第3,6题;3、弹性作业:谢谢!温故知新若将常数改为大于|F1F2| ,则轨迹双曲线定义:平面内与两个定点F1,F2的距离的差的 等于正常数 的点的轨迹叫做双曲线。这两个定点F1,F2叫做双曲线的焦点,两焦点的距离| F1F2|叫做双曲线的焦距。若没有“绝对值”,则轨迹是双曲线的一支;以F1 ,F2 为端点的两条射线;不存在;若将常数改为等于|F1F2| ,则轨迹是若常数为0,则轨迹是线段F1F2的垂直平分线。数学探究绝对值 (小于|F1F2| )所求轨迹的方程为:例1. 已知 , 动点 到 、 的距离之差的绝对值为6,求点 的轨迹方程.两条射线轨迹不存在上节课回顾线段F1F2的中垂线练习.一炮弹在某处爆炸,在 F1 (-5000,0)处听到爆炸声的时间比在F2(5000,0)处 晚 秒,已知坐标轴的单位长度为1米,声速为340米/秒,爆炸点应在什么样的曲线上?并求爆炸点所在的曲线方程.
同学们:让我们一起走进:“美妙的数学花园”感受数学文化吧! 是一切重大科学技术发展的基础,是理性文明的火车头。数学若去掉“焦点在y轴上”这一条件,
解这道题能不能不讨论呢?分焦点在X轴上、y轴上两类情况讨论若焦点在 X轴上,设所求双曲线方程为 依题意得:{此时无解。故所求的双曲线方程仍为 焦点在 y轴上,双曲线方程为
