抛物线及其标准方程[上学期]
图片预览




文档简介
(共21张PPT)
抛物线及其标准方程
高中数学多媒体课件
垦利一中高二数学组
李军胜
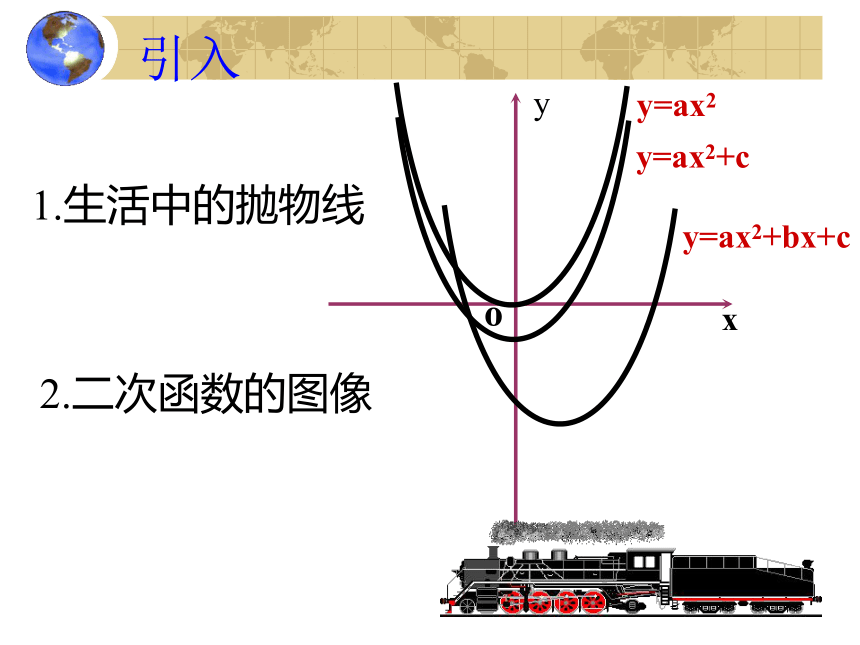
y
x
o
y=ax2+bx+c
y=ax2+c
y=ax2
引入
1.生活中的抛物线
2.二次函数的图像
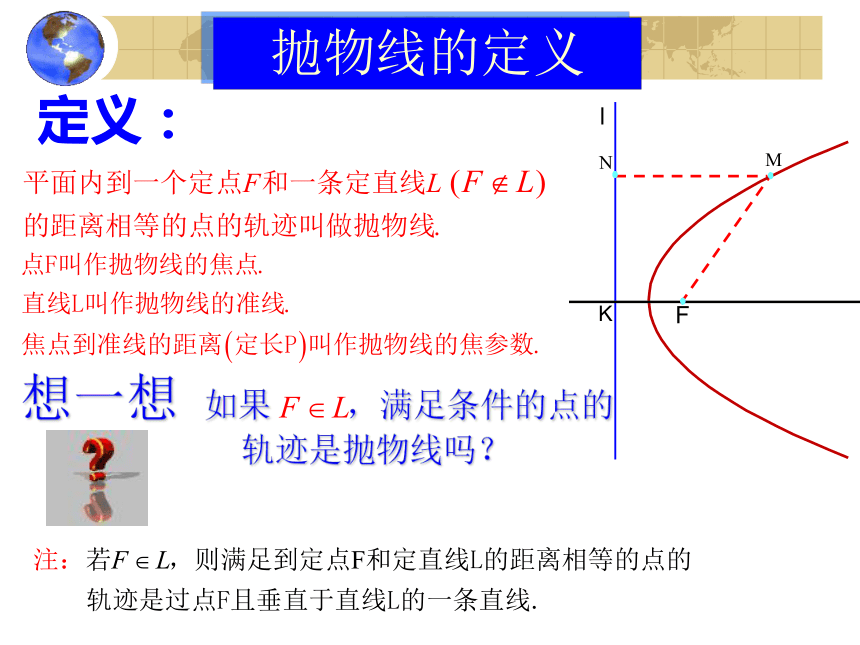
抛物线的定义
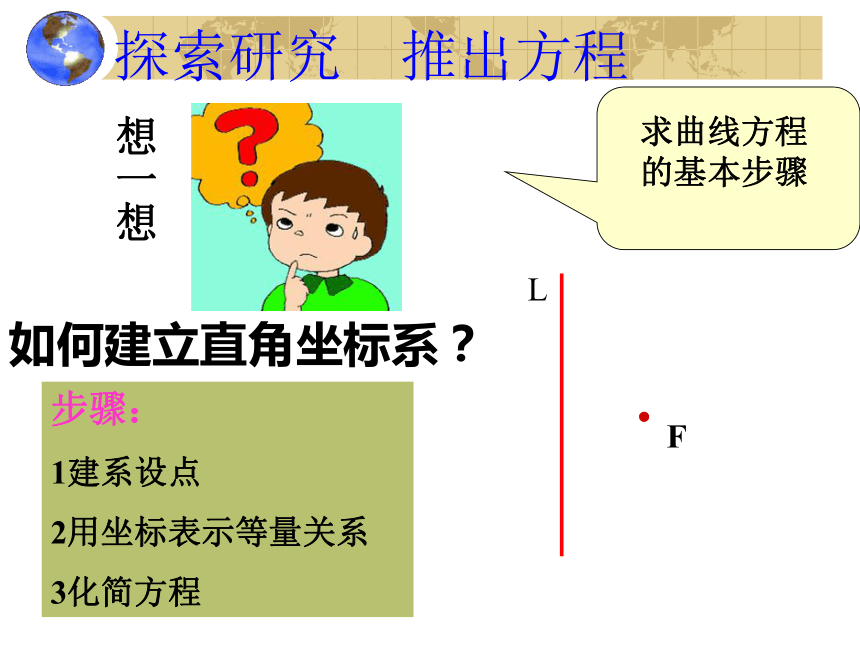
l
F
K
M
N
定义:
想一想 如果 ,满足条件的点的
轨迹是抛物线吗?
练一练
如何建立直角坐标系?
想一想
探索研究 推出方程
步骤:
1建系设点
2用坐标表示等量关系
3化简方程
求曲线方程的基本步骤
·
F
L
x
o
y
L
F
x
y
o
L
F
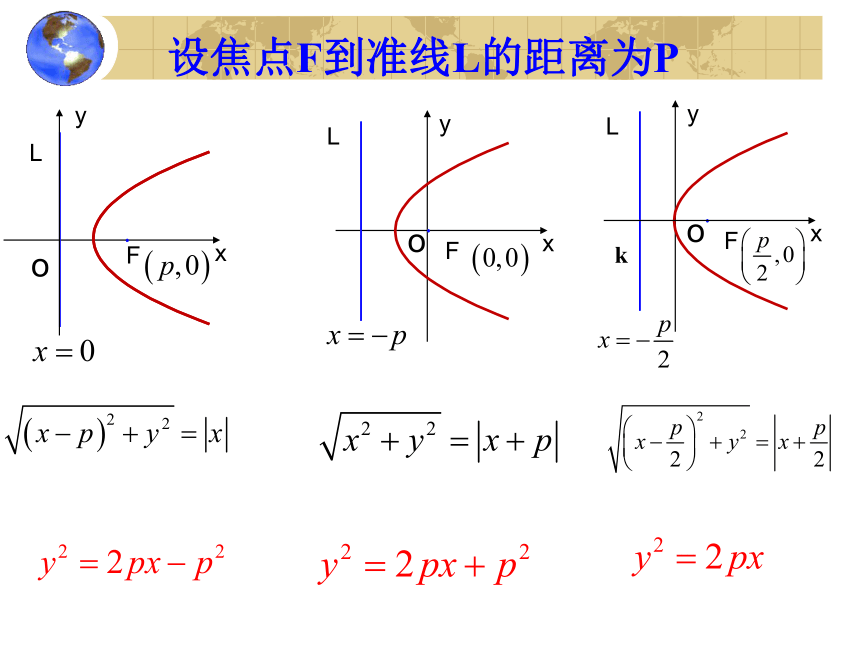
设焦点F到准线L的距离为P
y
o
L
F
x
k
. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.
说明:
p的几何意义: 焦点到准线的距离.
x
它所表示的抛物线的焦点F在 x 轴的正半轴上,坐标是( ),它的
准线方程是 .
y
o
L
F
已知抛物线的标准方程,
求其焦点坐标和准线方程.
标准方程 焦点坐标 准线方程
巩固练习1
(3)若焦点在x轴正半轴上, 且焦点与准线间 的距离为6.
(2)若准线方程 是
巩固练习2 求抛物线的标准方程
(1)抛物线的焦点是F(3,0),
抛物线的标准方程
抛物线的焦点坐标和准线方程:
关键:确定P的值
例2:定义的应用
x
y
F
P
N
x
y
F
P
N
x
y
F
M
N
K
小 结 :
1、抛物线、焦点、准线的定义.
4、注重数形结合的思想
2、抛物线的标准方程.
3、应用
(1)由定义和待定系数法求标准方程
(2)根据抛物线的定义求距离
作业:
课本P62 练习A 1,3
细练新教材P56 第11题
焦点F与准线l的相对位置还有以下三种情况:
对于这三种情况,应该分别怎样建立直角坐标系,
它们的标准方程又分别是什么?
想一想
课后探究
抛物线及其标准方程
高中数学多媒体课件
垦利一中高二数学组
李军胜
y
x
o
y=ax2+bx+c
y=ax2+c
y=ax2
引入
1.生活中的抛物线
2.二次函数的图像
抛物线的定义
l
F
K
M
N
定义:
想一想 如果 ,满足条件的点的
轨迹是抛物线吗?
练一练
如何建立直角坐标系?
想一想
探索研究 推出方程
步骤:
1建系设点
2用坐标表示等量关系
3化简方程
求曲线方程的基本步骤
·
F
L
x
o
y
L
F
x
y
o
L
F
设焦点F到准线L的距离为P
y
o
L
F
x
k
. ,叫作焦点在X轴正半轴上的
抛物线的标准方程.
说明:
p的几何意义: 焦点到准线的距离.
x
它所表示的抛物线的焦点F在 x 轴的正半轴上,坐标是( ),它的
准线方程是 .
y
o
L
F
已知抛物线的标准方程,
求其焦点坐标和准线方程.
标准方程 焦点坐标 准线方程
巩固练习1
(3)若焦点在x轴正半轴上, 且焦点与准线间 的距离为6.
(2)若准线方程 是
巩固练习2 求抛物线的标准方程
(1)抛物线的焦点是F(3,0),
抛物线的标准方程
抛物线的焦点坐标和准线方程:
关键:确定P的值
例2:定义的应用
x
y
F
P
N
x
y
F
P
N
x
y
F
M
N
K
小 结 :
1、抛物线、焦点、准线的定义.
4、注重数形结合的思想
2、抛物线的标准方程.
3、应用
(1)由定义和待定系数法求标准方程
(2)根据抛物线的定义求距离
作业:
课本P62 练习A 1,3
细练新教材P56 第11题
焦点F与准线l的相对位置还有以下三种情况:
对于这三种情况,应该分别怎样建立直角坐标系,
它们的标准方程又分别是什么?
想一想
课后探究
