抛物线[上学期]
图片预览





文档简介
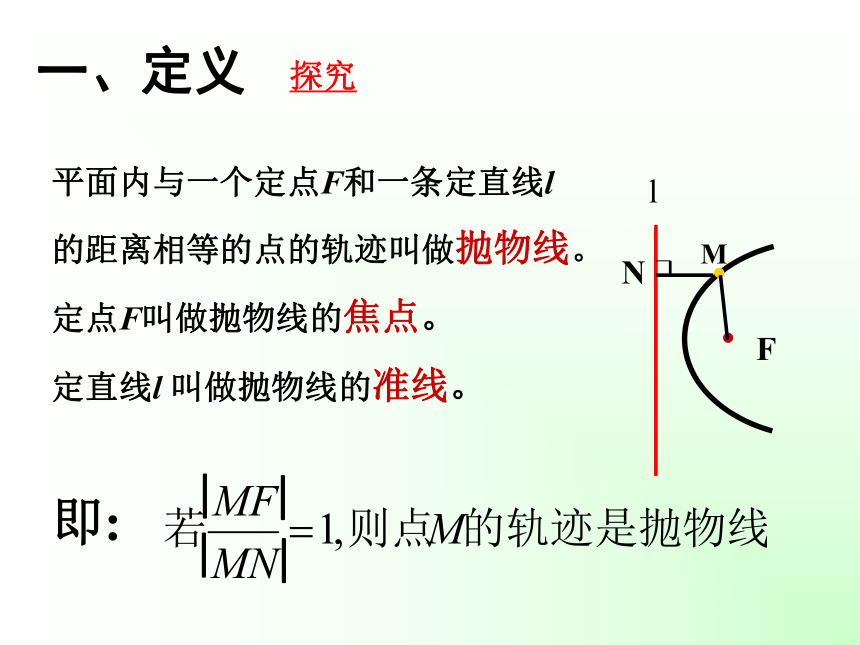
课件23张PPT。生活中的抛物线抛物线及其标准方程平面内与一个定点F和一条定直线l
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
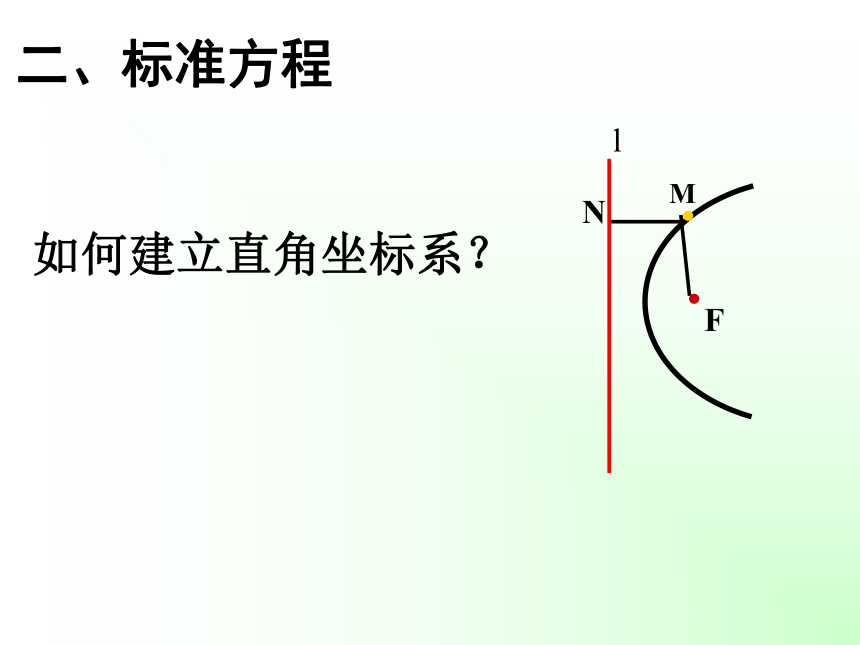
一、定义探究二、标准方程如何建立直角坐标系?二、标准方程K设︱KF︱= p设点M的坐标为(x,y), 由定义可知, 方程 y2 = 2px(p>0)叫做抛物线的标准方程。 焦 点 到 准 线 的 距 离其中p为正常数,它的几何意义是它表示的抛物线的焦点在X轴的正半轴上
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式。
想一想:
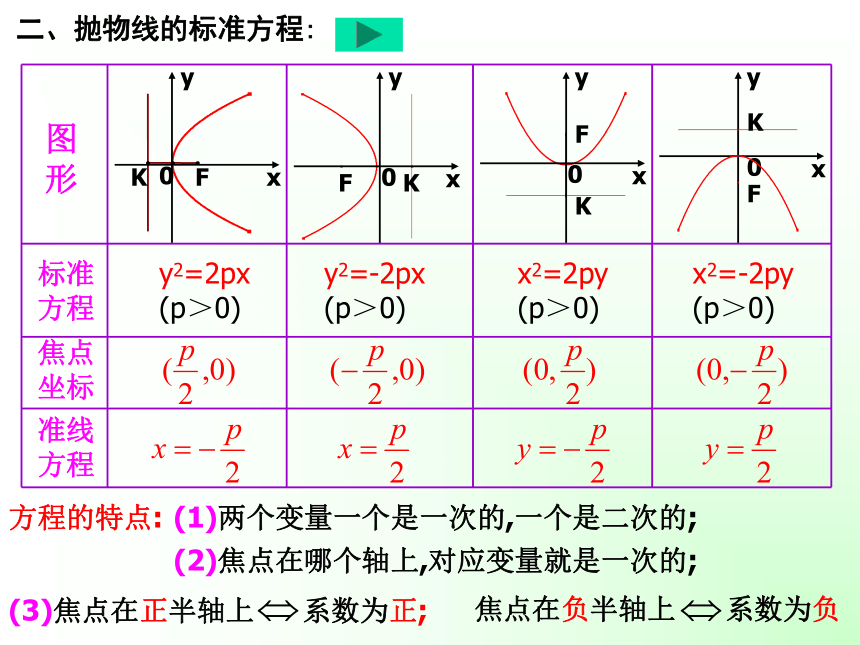
抛物线的位置及其方程还有没有其它的形式?二、抛物线的标准方程:y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)方程的特点:(1)两个变量一个是一次的,一个是二次的;(2)焦点在哪个轴上,对应变量就是一次的;三、例题与练习:1.判断下列方程是否表示抛物线,若是,求出焦点坐标和准线方程.(1)4y2-9y=36(2)x2=y(3)y2+2x=0(4)不是2.求满足条件的抛物线的标准方程.(1)准线方程为x=2;(2)焦点坐标为(0,-2);(3)焦点到准线的距离为3;y2=-8xx2=-8yx2=±6y 或 y2=±6x(4)顶点在坐标原点焦点在y轴上,且过点(-1,-3);(5) 顶点为原点对称轴为坐标轴且过点(4,-8).x2=-2y 或 y2=16x(6)顶点为原点,焦点在坐标轴且过直线x-2y-4=0B小 结 :1、抛物线的定义、标准方程类型与图象的
对应关系及其判断方法。判断方法2、抛物线的标准方程和它的焦点、准线 方程。y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)y2=2px (p>0)平面内到定点F的距离与到定直线l 的距离相等的点的轨迹.其中定点F是抛物线的焦点;定直线l 叫抛物线的准线. 抛物线及其标准方程解:由条件知,M与F的距离与M到直线x+4=0的距离相等∴M的轨迹是焦点在F 的抛物线,且∴M的轨迹方程是y2=16xx2=8y(4)离心率:抛物线上的点M到焦点的距离和它到准线的距离的比叫做抛物线的离心率,用e表示,e=1抛物线的几何性质:以y2=2px(p>0)为例
(1)范围:x≥0,y∈k
(2)对称性:关于x轴对称
(3)顶点:抛物线与对称轴的交点叫抛物线的顶点。
(标准方程对应的抛物线的顶点是坐标原点)解: 由条件知直线AB的方程为y=x-1x2-6x+1=0方法2:设A和B的横坐标分别为x1和x2则|AF|=x1+1, |BF|=x2+1∴|AB|=x1+x2+2y=x+1或y=-x+1变题:例3中若经过焦点的直线截抛物线所得弦的中点横坐标是3,求弦AB的长 。焦点弦:指过抛物线焦点的直线被抛物线所截的线段P1P2,其实质是两条焦半径共线。 yx例4、过抛物线y2=2px(p>0)的焦点的一条直线和此抛物线相交,两个交点的纵坐标为y1、y2,
求证: y1 ·y2=-p2 x1x2=?思考:经过抛物线y2=2px (p>0)的焦点F的一条直线和这抛物线相交于两点P1,P2 ,则以线段P1P2为直径的圆与准线的位置关系是怎么?经过抛物线y2=2px(p>0)的焦点F的直线l的特点1、若直线l与抛物线有交点A (x1,y1) 、B (x2,y2),
则AB=2、若AB的中点为C(x0,y0),则AB=3、 y1 ·y2= ; x1 · x2=4、以焦点弦为直径的圆必与准线________.归纳:相切x1+ x2+p2x0+p-p2例5:过抛物线焦点F的直线交抛物线于A,B两点,通过
点A和抛物线顶点的直线交抛物线的准线于点D,求证:
直线DB平行于抛物线的对称轴。例6:已知抛物线的方程为y2=4x,直线l过定点
P(-2,1),斜率为k,k为何值时,直线l与抛物线y2=4x:
只有一个公共点;有两个公共点;没有公共点?
作图补充例题与练习解: 如图,设|PQ|为P到准线的距离则|PF|=|PQ|∴|AP|+|PF|=|AP|+|PQ|∴当A,P,Q共线时, |AP|+|PF|最小即P点坐标为(2,2)时, |AP|+|PF|最小,
且最小值为 .变式:若把题目中A的坐标改为为(2,3)时,此时最小
值是多少呢? ( 1 ) : 一次项的变量如果为X(或Y),则X轴(或Y轴)为抛物线的对称轴,焦点就在对称轴上。
( 2 ) :一次项的系数的符号决定了开口方向。 判断方法例1、求过点A(-3,2)的抛物线的
标准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
的距离相等的点的轨迹叫做抛物线。
定点F叫做抛物线的焦点。
定直线l 叫做抛物线的准线。
一、定义探究二、标准方程如何建立直角坐标系?二、标准方程K设︱KF︱= p设点M的坐标为(x,y), 由定义可知, 方程 y2 = 2px(p>0)叫做抛物线的标准方程。 焦 点 到 准 线 的 距 离其中p为正常数,它的几何意义是它表示的抛物线的焦点在X轴的正半轴上
一条抛物线,由于它在坐标平面内的位置不同,方程也不同,所以抛物线的标准方程还有其它形式。
想一想:
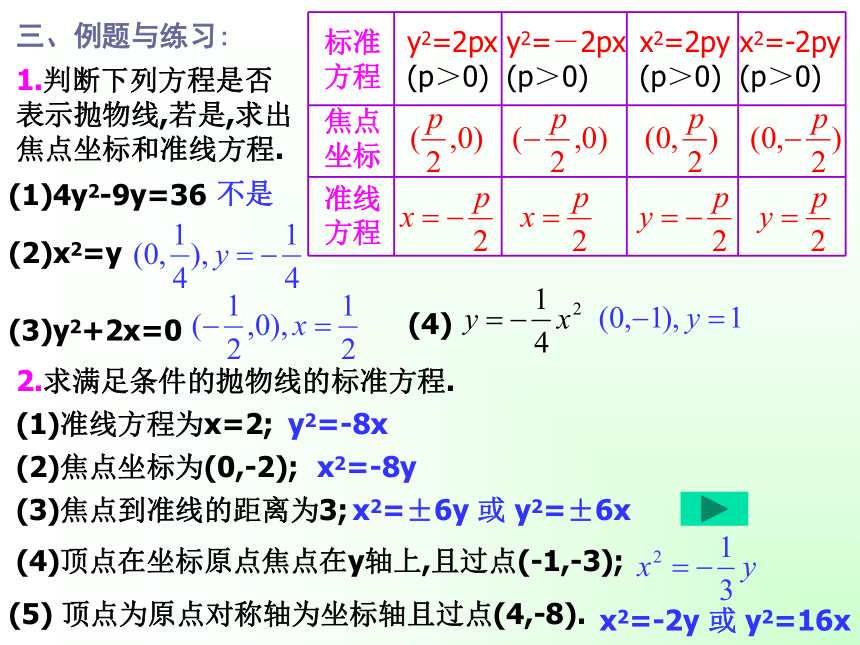
抛物线的位置及其方程还有没有其它的形式?二、抛物线的标准方程:y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)方程的特点:(1)两个变量一个是一次的,一个是二次的;(2)焦点在哪个轴上,对应变量就是一次的;三、例题与练习:1.判断下列方程是否表示抛物线,若是,求出焦点坐标和准线方程.(1)4y2-9y=36(2)x2=y(3)y2+2x=0(4)不是2.求满足条件的抛物线的标准方程.(1)准线方程为x=2;(2)焦点坐标为(0,-2);(3)焦点到准线的距离为3;y2=-8xx2=-8yx2=±6y 或 y2=±6x(4)顶点在坐标原点焦点在y轴上,且过点(-1,-3);(5) 顶点为原点对称轴为坐标轴且过点(4,-8).x2=-2y 或 y2=16x(6)顶点为原点,焦点在坐标轴且过直线x-2y-4=0B小 结 :1、抛物线的定义、标准方程类型与图象的
对应关系及其判断方法。判断方法2、抛物线的标准方程和它的焦点、准线 方程。y2=-2px (p>0)x2=2py (p>0)x2=-2py (p>0)y2=2px (p>0)平面内到定点F的距离与到定直线l 的距离相等的点的轨迹.其中定点F是抛物线的焦点;定直线l 叫抛物线的准线. 抛物线及其标准方程解:由条件知,M与F的距离与M到直线x+4=0的距离相等∴M的轨迹是焦点在F 的抛物线,且∴M的轨迹方程是y2=16xx2=8y(4)离心率:抛物线上的点M到焦点的距离和它到准线的距离的比叫做抛物线的离心率,用e表示,e=1抛物线的几何性质:以y2=2px(p>0)为例
(1)范围:x≥0,y∈k
(2)对称性:关于x轴对称
(3)顶点:抛物线与对称轴的交点叫抛物线的顶点。
(标准方程对应的抛物线的顶点是坐标原点)解: 由条件知直线AB的方程为y=x-1x2-6x+1=0方法2:设A和B的横坐标分别为x1和x2则|AF|=x1+1, |BF|=x2+1∴|AB|=x1+x2+2y=x+1或y=-x+1变题:例3中若经过焦点的直线截抛物线所得弦的中点横坐标是3,求弦AB的长 。焦点弦:指过抛物线焦点的直线被抛物线所截的线段P1P2,其实质是两条焦半径共线。 yx例4、过抛物线y2=2px(p>0)的焦点的一条直线和此抛物线相交,两个交点的纵坐标为y1、y2,
求证: y1 ·y2=-p2 x1x2=?思考:经过抛物线y2=2px (p>0)的焦点F的一条直线和这抛物线相交于两点P1,P2 ,则以线段P1P2为直径的圆与准线的位置关系是怎么?经过抛物线y2=2px(p>0)的焦点F的直线l的特点1、若直线l与抛物线有交点A (x1,y1) 、B (x2,y2),
则AB=2、若AB的中点为C(x0,y0),则AB=3、 y1 ·y2= ; x1 · x2=4、以焦点弦为直径的圆必与准线________.归纳:相切x1+ x2+p2x0+p-p2例5:过抛物线焦点F的直线交抛物线于A,B两点,通过
点A和抛物线顶点的直线交抛物线的准线于点D,求证:
直线DB平行于抛物线的对称轴。例6:已知抛物线的方程为y2=4x,直线l过定点
P(-2,1),斜率为k,k为何值时,直线l与抛物线y2=4x:
只有一个公共点;有两个公共点;没有公共点?
作图补充例题与练习解: 如图,设|PQ|为P到准线的距离则|PF|=|PQ|∴|AP|+|PF|=|AP|+|PQ|∴当A,P,Q共线时, |AP|+|PF|最小即P点坐标为(2,2)时, |AP|+|PF|最小,
且最小值为 .变式:若把题目中A的坐标改为为(2,3)时,此时最小
值是多少呢? ( 1 ) : 一次项的变量如果为X(或Y),则X轴(或Y轴)为抛物线的对称轴,焦点就在对称轴上。
( 2 ) :一次项的系数的符号决定了开口方向。 判断方法例1、求过点A(-3,2)的抛物线的
标准方程。解:当抛物线的焦点在y轴
的正半轴上时,把A(-3,2)
代入x2 =2py,得p= 当焦点在x轴的负半轴上时,
把A(-3,2)代入y2 = -2px,
得p=
∴抛物线的标准方程为x2 = y或y2 = x 。
