抛物线及其标准方程第一课时[上学期]
文档属性
| 名称 | 抛物线及其标准方程第一课时[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 237.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-09 00:00:00 | ||
图片预览



文档简介
课件15张PPT。抛物线及其标准方程第一课时目标1.掌握抛物线的定义及其标准方程;
2.进一步熟悉坐标法,能根据已知条件用坐标法求抛物线的方程;
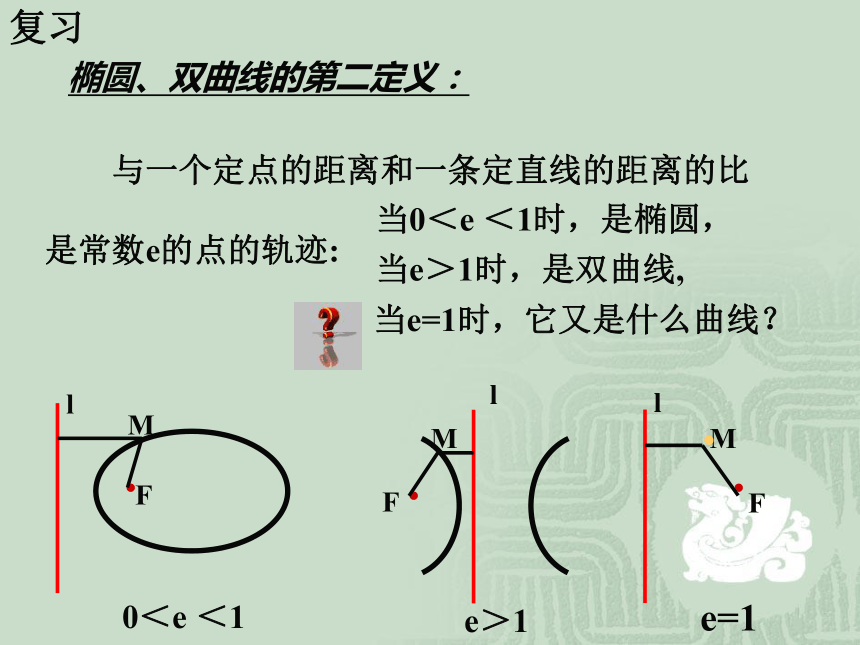
3.会根据条件确定抛物线的标准方程及焦点坐标,准线方程,画抛物线的草图.复习椭圆、双曲线的第二定义: 与一个定点的距离和一条定直线的距离的比
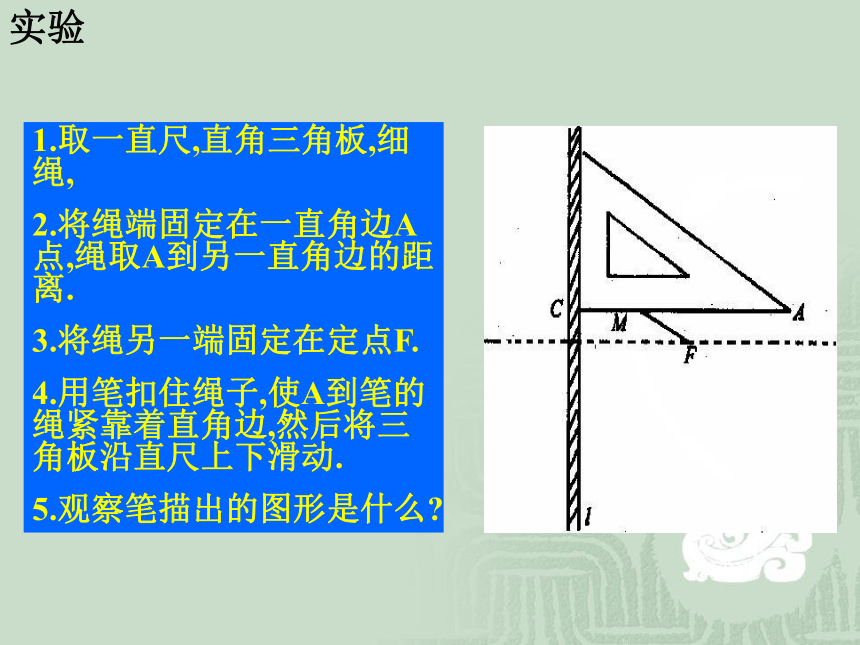
是常数e的点的轨迹: 当e>1时,是双曲线,当e=1时,它又是什么曲线?当0<e <1时,是椭圆,1.取一直尺,直角三角板,细绳,
2.将绳端固定在一直角边A点,绳取A到另一直角边的距离.
3.将绳另一端固定在定点F.
4.用笔扣住绳子,使A到笔的绳紧靠着直角边,然后将三角板沿直尺上下滑动.
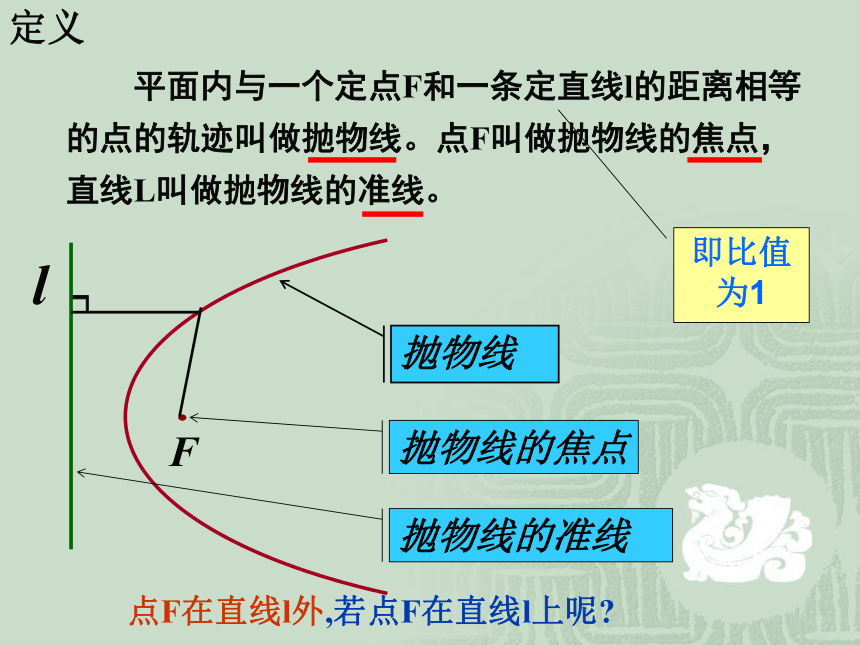
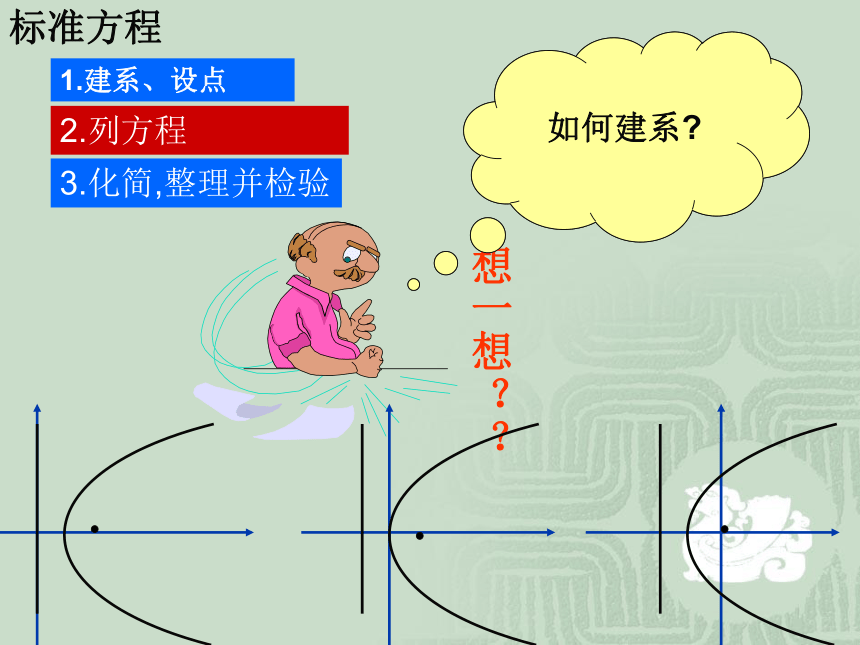
5.观察笔描出的图形是什么?实验演示定义 平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。点F叫做抛物线的焦点,直线L叫做抛物线的准线。 抛物线抛物线的焦点抛物线的准线┑即比值为1点F在直线l外,若点F在直线l上呢?标准方程1.建系、设点2.列方程3.化简,整理并检验求曲线方程的一般步骤是什么?
如何建系?y2=2px-p2y2=2pxy2=2px+p2抛物线的标准方程其焦点在x轴的正半轴上为(p/2,0),准线方程为 x=-p/2xyOxxyyOOFFF若焦点到准线的距离为p,按上述方式建系,求其方程.
左图抛物线的方程是什么?y=ax2
焦点坐标,准线方程为什么?焦点坐标:(0,p/2); 准线方程:y=-p/2xyO小结y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)说明四种抛物线标准方程之比较顶点为原点对称轴为坐标轴p为焦点到准线的距离顶点到焦点的距离等于顶点到准线的距离为p/2一次变量为x(y),则对称轴为x(y)轴焦点在x(y)轴正半轴上,则开口向右(上);
焦点在x(y)轴负半轴上,则开口向左(下);例题例1: (1)已知抛物线的标准方程是y2 = 6x,求它的焦点坐标和准线方程;变题1:已知抛物线的方程是y = -6x2,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程。变题2:已知抛物线的方程是y = 4ax2(a<0),求它的焦点坐标和准线方程;变题3:已知抛物线的焦点在直线3x-4y-12=0上,求其标准方程.(1)定位(焦点位置)、(2)定形(求p)例2.动点M与点F(4,0)的距离比它到直线x+5=0的距离小1,求点M的轨迹方程.变题:动点M与点F(0,4)的距离比它到直线y+3=0的距离大1,求点M的轨迹方程.小结1.抛物线的定义;
2.抛物线的标准方程;(1)定位(焦点位置)、(2)定形(求p)3.由条件求抛物线方程的方法;
4.由方程写其焦点坐标、准线方程.作业1.求过点P(4,-2)的抛物线的标准方程;
2.抛物线y2=2px(p>0)上一点M与焦点F的距离为2p,求点M的坐标;
3.求抛物线y=ax2(a≠0)的焦点坐标和准线方程;
4.动圆M过点P(0,2)且与直线y+2=0相切,求动圆圆心M的轨迹方程.
2.进一步熟悉坐标法,能根据已知条件用坐标法求抛物线的方程;
3.会根据条件确定抛物线的标准方程及焦点坐标,准线方程,画抛物线的草图.复习椭圆、双曲线的第二定义: 与一个定点的距离和一条定直线的距离的比
是常数e的点的轨迹: 当e>1时,是双曲线,当e=1时,它又是什么曲线?当0<e <1时,是椭圆,1.取一直尺,直角三角板,细绳,
2.将绳端固定在一直角边A点,绳取A到另一直角边的距离.
3.将绳另一端固定在定点F.
4.用笔扣住绳子,使A到笔的绳紧靠着直角边,然后将三角板沿直尺上下滑动.
5.观察笔描出的图形是什么?实验演示定义 平面内与一个定点F和一条定直线l的距离相等的点的轨迹叫做抛物线。点F叫做抛物线的焦点,直线L叫做抛物线的准线。 抛物线抛物线的焦点抛物线的准线┑即比值为1点F在直线l外,若点F在直线l上呢?标准方程1.建系、设点2.列方程3.化简,整理并检验求曲线方程的一般步骤是什么?
如何建系?y2=2px-p2y2=2pxy2=2px+p2抛物线的标准方程其焦点在x轴的正半轴上为(p/2,0),准线方程为 x=-p/2xyOxxyyOOFFF若焦点到准线的距离为p,按上述方式建系,求其方程.
左图抛物线的方程是什么?y=ax2
焦点坐标,准线方程为什么?焦点坐标:(0,p/2); 准线方程:y=-p/2xyO小结y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)说明四种抛物线标准方程之比较顶点为原点对称轴为坐标轴p为焦点到准线的距离顶点到焦点的距离等于顶点到准线的距离为p/2一次变量为x(y),则对称轴为x(y)轴焦点在x(y)轴正半轴上,则开口向右(上);
焦点在x(y)轴负半轴上,则开口向左(下);例题例1: (1)已知抛物线的标准方程是y2 = 6x,求它的焦点坐标和准线方程;变题1:已知抛物线的方程是y = -6x2,求它的焦点坐标和准线方程;
(2)已知抛物线的焦点坐标是F(0,-2), 求它的标准方程。变题2:已知抛物线的方程是y = 4ax2(a<0),求它的焦点坐标和准线方程;变题3:已知抛物线的焦点在直线3x-4y-12=0上,求其标准方程.(1)定位(焦点位置)、(2)定形(求p)例2.动点M与点F(4,0)的距离比它到直线x+5=0的距离小1,求点M的轨迹方程.变题:动点M与点F(0,4)的距离比它到直线y+3=0的距离大1,求点M的轨迹方程.小结1.抛物线的定义;
2.抛物线的标准方程;(1)定位(焦点位置)、(2)定形(求p)3.由条件求抛物线方程的方法;
4.由方程写其焦点坐标、准线方程.作业1.求过点P(4,-2)的抛物线的标准方程;
2.抛物线y2=2px(p>0)上一点M与焦点F的距离为2p,求点M的坐标;
3.求抛物线y=ax2(a≠0)的焦点坐标和准线方程;
4.动圆M过点P(0,2)且与直线y+2=0相切,求动圆圆心M的轨迹方程.
