抛物线及其标准方程第二课时[上学期]
文档属性
| 名称 | 抛物线及其标准方程第二课时[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 213.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-09 00:00:00 | ||
图片预览





文档简介
课件12张PPT。抛物线及其标准方程第二课时目标1.熟练掌握抛物线的定义,并会求抛物线的标准方程或轨迹方程;
2. 能利用抛物线的定义(焦半径)解决一些问题;
3. 掌握过抛物线焦点的有关弦长问题及处理方法.复习1.抛物线的定义;
2.抛物线的标准方程及其焦点坐标和准线方程.3.由条件求抛物线方程的方法;
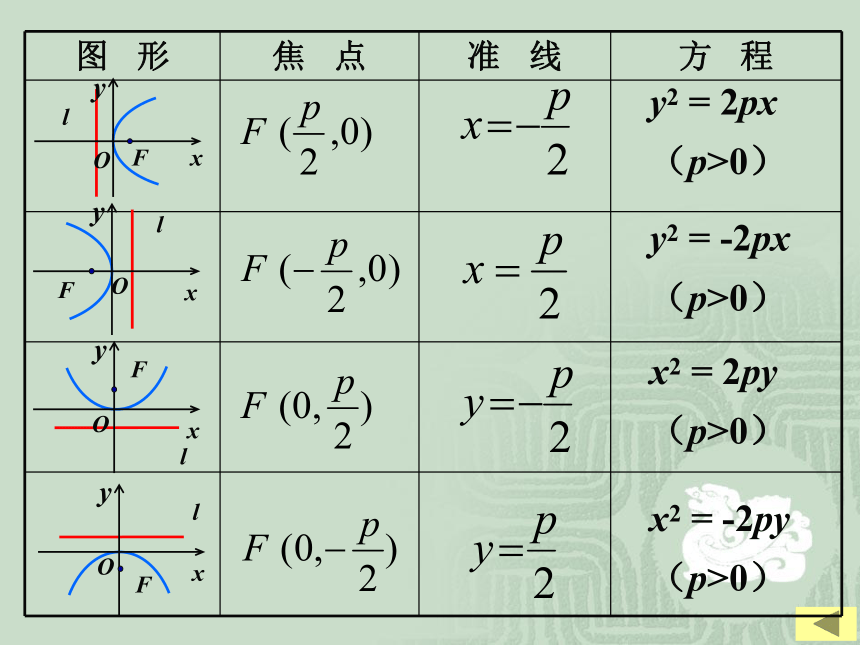
4.由抛物线标准方程确定焦点坐标及准线方程的方法.(1)定位(焦点位置)、(2)定形(求p)y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)例题例1.已知动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切,求动圆圆心的轨迹方程.将条件转化为距离相等,从而避免了
直接法求方程的繁琐化简例2.已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值.将抛物线上点到焦点的距离转化为
到准线的距离(定义)抛物线y2=2px(p>0)上一点P(x0,y0)到焦点的距离转化为到准线的距离有:|PF|=x0+p/2,这就是抛物线的焦半径公式.y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)在抛物线y2=2x上求一点P,使P到焦点F与到点A(3,2)的距离之和最小.变题引申例3.斜率为1的直线经过抛物线y2=4x的焦点,与抛物线相交于A、B两点,求线段AB的长.过抛物线y2=2px(p>0)焦点的弦长
|AB|=x1+x2+p例4.控照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60cm,灯深为40cm,求抛物线的标准方程和焦点位置.FyxOAB思考:课后能否证明过抛物线焦点的光线被镜面反射后的么射光线与轴平行.小结1.求抛物线标准方程的方法;
2.抛物线的焦半径(定义)及其应用.3.过抛物线的焦点的又一弦长公式过抛物线y2=2px(p>0)焦点的弦长
|AB|=x1+x2+p作业1.已知动圆M与y轴相切,且与定圆C:x2+y2=2ax(a>0)外切,求动圆圆心M的轨迹方程.
2.求证:以抛物线的焦点弦为直径的圆与抛物线的准线相切.
(思考:椭圆与双曲线呢?)
3.过抛物线y2=2px(p>0)的焦点的一条直线与抛物线相交,两个交点的坐标为(x1,y1),(x2,y2),
求证:x1x2=p2/4;y1y2=-p2.
2. 能利用抛物线的定义(焦半径)解决一些问题;
3. 掌握过抛物线焦点的有关弦长问题及处理方法.复习1.抛物线的定义;
2.抛物线的标准方程及其焦点坐标和准线方程.3.由条件求抛物线方程的方法;
4.由抛物线标准方程确定焦点坐标及准线方程的方法.(1)定位(焦点位置)、(2)定形(求p)y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)例题例1.已知动圆M与直线y=2相切,且与定圆C:x2+(y+3)2=1外切,求动圆圆心的轨迹方程.将条件转化为距离相等,从而避免了
直接法求方程的繁琐化简例2.已知抛物线的顶点在原点,对称轴为x轴,抛物线上的点M(-3,m)到焦点的距离等于5,求抛物线的方程和m的值.将抛物线上点到焦点的距离转化为
到准线的距离(定义)抛物线y2=2px(p>0)上一点P(x0,y0)到焦点的距离转化为到准线的距离有:|PF|=x0+p/2,这就是抛物线的焦半径公式.y2 = 2px
(p>0)y2 = -2px
(p>0)x2 = 2py
(p>0)x2 = -2py
(p>0)在抛物线y2=2x上求一点P,使P到焦点F与到点A(3,2)的距离之和最小.变题引申例3.斜率为1的直线经过抛物线y2=4x的焦点,与抛物线相交于A、B两点,求线段AB的长.过抛物线y2=2px(p>0)焦点的弦长
|AB|=x1+x2+p例4.控照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口圆的直径为60cm,灯深为40cm,求抛物线的标准方程和焦点位置.FyxOAB思考:课后能否证明过抛物线焦点的光线被镜面反射后的么射光线与轴平行.小结1.求抛物线标准方程的方法;
2.抛物线的焦半径(定义)及其应用.3.过抛物线的焦点的又一弦长公式过抛物线y2=2px(p>0)焦点的弦长
|AB|=x1+x2+p作业1.已知动圆M与y轴相切,且与定圆C:x2+y2=2ax(a>0)外切,求动圆圆心M的轨迹方程.
2.求证:以抛物线的焦点弦为直径的圆与抛物线的准线相切.
(思考:椭圆与双曲线呢?)
3.过抛物线y2=2px(p>0)的焦点的一条直线与抛物线相交,两个交点的坐标为(x1,y1),(x2,y2),
求证:x1x2=p2/4;y1y2=-p2.
