抛物线的简单几何性质第二课时[上学期]
文档属性
| 名称 | 抛物线的简单几何性质第二课时[上学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 270.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-01-09 00:00:00 | ||
图片预览




文档简介
课件13张PPT。抛物线的几何性质第二课时目标1.巩固抛物线的标准方程、几何性质等有关知识;
2.会用二次方程根的判别式,根与系数的关系判定直线与抛物线的关系;
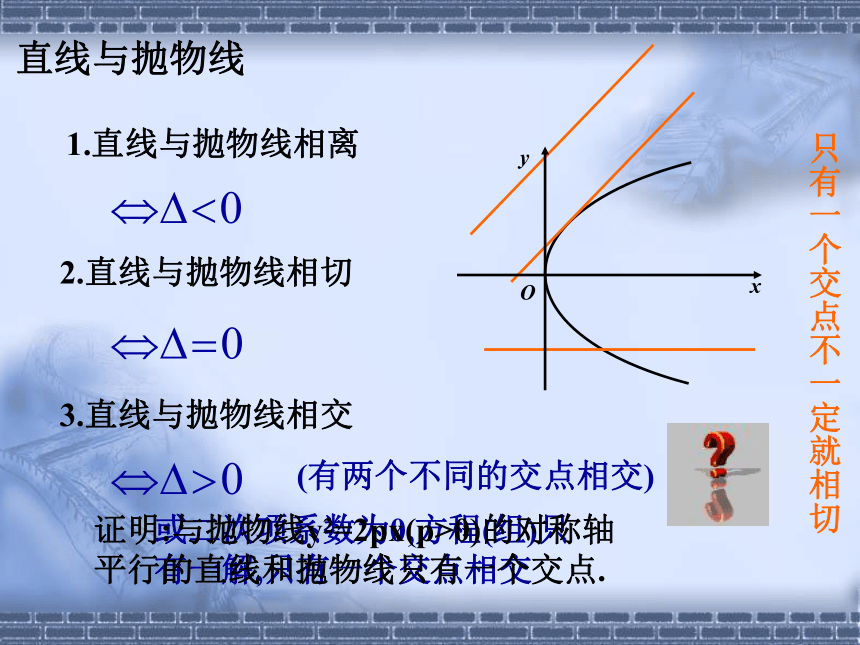
3.掌握直线与抛物线焦点弦有关的问题.点与抛物线点与圆、椭圆、双曲线的位置关系及判断方法.点P(x0,y0)与抛物线y2=2px(p>0)的位置关系及判断方法.1.点在抛物线外2.点在抛物线上3.点在抛物线内y02-2px0>0y02-2px0=0y02-2px0<0直线与抛物线1.直线与抛物线相离3.直线与抛物线相交2.直线与抛物线相切xOy(有两个不同的交点相交)或二次项系数为0,方程(组)只有一解,只有一个交点相交证明:与抛物线y2=2px(p>0)的对称轴平行的直线和抛物线只有一个交点.只有一个交点不一定就相切结论1.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交点为A(x1,y1)、B(x2,y2),则
(1)x1x2=p2/4; (2)y1y2=-p2; (3)|AB|=x1+x2+p
(4)若直线AB的倾斜角为θ,则|AB|=2p/sin2 θ
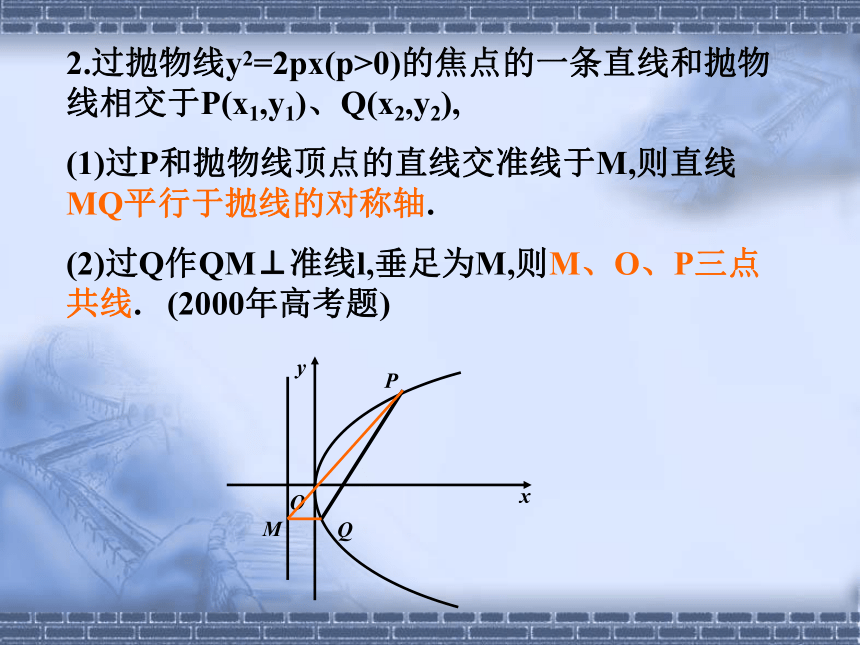
(5)以AB为直径的圆与准线相切.ABθ2.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交于P(x1,y1)、Q(x2,y2),
(1)过P和抛物线顶点的直线交准线于M,则直线MQ平行于抛线的对称轴.
(2)过Q作QM⊥准线l,垂足为M,则M、O、P三点共线. (2000年高考题)M练习1.已知直线l过点A(-3p/2,p)且与抛物线y2=2px(p>0)只有一个公共点,则直线l的条数为 .2.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交于P(x1,y1)、Q(x2,y2),则y1y2=-p2是直线PQ过抛物线焦点的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件例题1.AB是抛物线y2=2px(p>0)上两点,满足OA⊥OB(O为坐标原点),求证:
(1)A、B两点的横坐标之积、纵坐标之积均为定值;(2)直线AB经过一定点.(1)逆命题:若横坐标之积为定值4p2(或纵坐标之积为定值-4p2),是否有OA⊥OB?(2)逆命题:若直线AB过定点(2p,0), 是否有OA⊥OB?结论抛物线y2=2px(p>0)的轴上有三个点:
(1)焦点F:有许多关于焦点弦有关的结论;(2)点(2p,0):过该点的直线与抛物线交于两点A(x1,y1),B(x2,y2),有
x1x2=4p2;y1y2=-4p2;
OA ⊥ OB(3)点M(p,0):P为抛物线上任一点,
在轴上M点左侧的点,有|PM|的最小值为|OM|
在轴上M点右侧的点, 到顶点的距离不是最小.例题2.如果抛物线y=ax2-1上总有关于直线x+y=0对称的相异两点,试求a的范围.小结1.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交点为A(x1,y1)、B(x2,y2),则
(1)x1x2=p2/4; (2)y1y2=-p2; (3)|AB|=x1+x2+p/2
(4)若直线AB的倾斜角为θ,则|AB|=2p/sin2 θ
(5)以AB为直径的圆与准线相切.2.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交于P(x1,y1)、Q(x2,y2),
(1)过P和抛物线顶点的直线交准线于M,则直线MQ平行于抛线的对称轴.
(2)过Q作QM⊥准线l,垂足为M,则M、O、P三点共线. (2000年高考题)抛物线y2=2px(p>0)的轴上有三个点:
(1)焦点F:有许多关于焦点弦有关的结论;(2)点(2p,0):过该点的直线与抛物线交于两点A(x1,y1),B(x2,y2),有
x1x2=4p2;y1y2=-4p2;
OA ⊥ OB(3)点M(p,0):P为抛物线上任一点,
在轴上M点左侧的点,有|PM|的最小值为|OM|
在轴上M点右侧的点, 到顶点的距离不是最小.作业1.在抛物线y2=2x上求一点P,使P到直线x-y+3=0的距离最短,并求出距离的最小值.
2.若直线过定点M(m,0)(m>0)与抛物线y2=2px(p>0)交于A(x1,y1)、B(x2,y2),求证:x1x2=m2;y1y2=-2pm.
3.抛物线y2=2px(p>0)的焦点为F,AB为抛物线的焦点弦,求证:
4. AB为抛物线y2=2px(p>0)的焦点弦,A、B在准线上的射影分别为M、N,求证:以MN为直径的圆与AB相切于焦点F.
2.会用二次方程根的判别式,根与系数的关系判定直线与抛物线的关系;
3.掌握直线与抛物线焦点弦有关的问题.点与抛物线点与圆、椭圆、双曲线的位置关系及判断方法.点P(x0,y0)与抛物线y2=2px(p>0)的位置关系及判断方法.1.点在抛物线外2.点在抛物线上3.点在抛物线内y02-2px0>0y02-2px0=0y02-2px0<0直线与抛物线1.直线与抛物线相离3.直线与抛物线相交2.直线与抛物线相切xOy(有两个不同的交点相交)或二次项系数为0,方程(组)只有一解,只有一个交点相交证明:与抛物线y2=2px(p>0)的对称轴平行的直线和抛物线只有一个交点.只有一个交点不一定就相切结论1.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交点为A(x1,y1)、B(x2,y2),则
(1)x1x2=p2/4; (2)y1y2=-p2; (3)|AB|=x1+x2+p
(4)若直线AB的倾斜角为θ,则|AB|=2p/sin2 θ
(5)以AB为直径的圆与准线相切.ABθ2.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交于P(x1,y1)、Q(x2,y2),
(1)过P和抛物线顶点的直线交准线于M,则直线MQ平行于抛线的对称轴.
(2)过Q作QM⊥准线l,垂足为M,则M、O、P三点共线. (2000年高考题)M练习1.已知直线l过点A(-3p/2,p)且与抛物线y2=2px(p>0)只有一个公共点,则直线l的条数为 .2.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交于P(x1,y1)、Q(x2,y2),则y1y2=-p2是直线PQ过抛物线焦点的
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.非充分非必要条件例题1.AB是抛物线y2=2px(p>0)上两点,满足OA⊥OB(O为坐标原点),求证:
(1)A、B两点的横坐标之积、纵坐标之积均为定值;(2)直线AB经过一定点.(1)逆命题:若横坐标之积为定值4p2(或纵坐标之积为定值-4p2),是否有OA⊥OB?(2)逆命题:若直线AB过定点(2p,0), 是否有OA⊥OB?结论抛物线y2=2px(p>0)的轴上有三个点:
(1)焦点F:有许多关于焦点弦有关的结论;(2)点(2p,0):过该点的直线与抛物线交于两点A(x1,y1),B(x2,y2),有
x1x2=4p2;y1y2=-4p2;
OA ⊥ OB(3)点M(p,0):P为抛物线上任一点,
在轴上M点左侧的点,有|PM|的最小值为|OM|
在轴上M点右侧的点, 到顶点的距离不是最小.例题2.如果抛物线y=ax2-1上总有关于直线x+y=0对称的相异两点,试求a的范围.小结1.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交,两交点为A(x1,y1)、B(x2,y2),则
(1)x1x2=p2/4; (2)y1y2=-p2; (3)|AB|=x1+x2+p/2
(4)若直线AB的倾斜角为θ,则|AB|=2p/sin2 θ
(5)以AB为直径的圆与准线相切.2.过抛物线y2=2px(p>0)的焦点的一条直线和抛物线相交于P(x1,y1)、Q(x2,y2),
(1)过P和抛物线顶点的直线交准线于M,则直线MQ平行于抛线的对称轴.
(2)过Q作QM⊥准线l,垂足为M,则M、O、P三点共线. (2000年高考题)抛物线y2=2px(p>0)的轴上有三个点:
(1)焦点F:有许多关于焦点弦有关的结论;(2)点(2p,0):过该点的直线与抛物线交于两点A(x1,y1),B(x2,y2),有
x1x2=4p2;y1y2=-4p2;
OA ⊥ OB(3)点M(p,0):P为抛物线上任一点,
在轴上M点左侧的点,有|PM|的最小值为|OM|
在轴上M点右侧的点, 到顶点的距离不是最小.作业1.在抛物线y2=2x上求一点P,使P到直线x-y+3=0的距离最短,并求出距离的最小值.
2.若直线过定点M(m,0)(m>0)与抛物线y2=2px(p>0)交于A(x1,y1)、B(x2,y2),求证:x1x2=m2;y1y2=-2pm.
3.抛物线y2=2px(p>0)的焦点为F,AB为抛物线的焦点弦,求证:
4. AB为抛物线y2=2px(p>0)的焦点弦,A、B在准线上的射影分别为M、N,求证:以MN为直径的圆与AB相切于焦点F.
