北师大版八年级上册 1勾股定理 复习课件(共21张PPT)
文档属性
| 名称 | 北师大版八年级上册 1勾股定理 复习课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 354.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览




文档简介
(共21张PPT)
北师大数学八年级上册
第一章 勾股定理
专题复习
如果直角三角形两直角边分别为a,b,斜边为c,
那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
已知Rt ABC的两直角边分别是3和4,则它的斜边是 .
5
勾股定理的应用条件
要点梳理
要点梳理
一、勾股定理
勾股定理的逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
勾股数
二、勾股定理的逆定理与勾股数
三、勾股定理的应用
例1 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm,
故直角三角形的面积是:
(cm2).
考点1 利用勾股定理求边长及面积
01 考点精讲
C
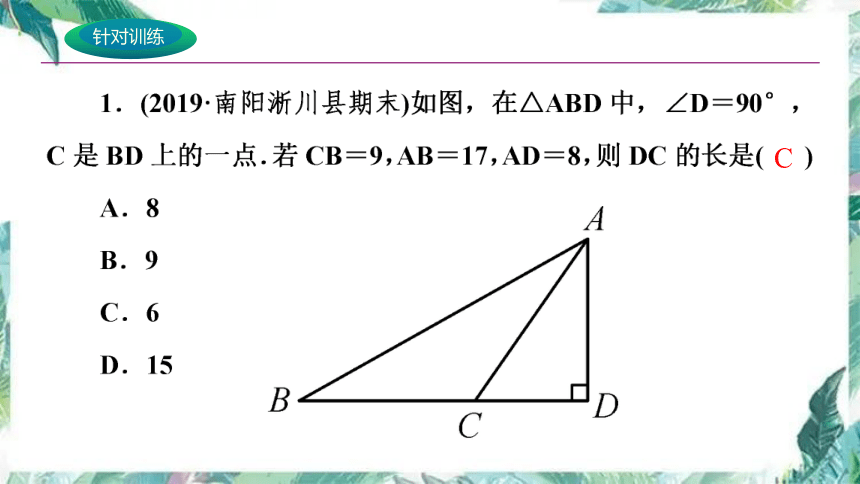
针对训练
考点2 利用勾股定理的逆定理判定三角形的形状或求角度
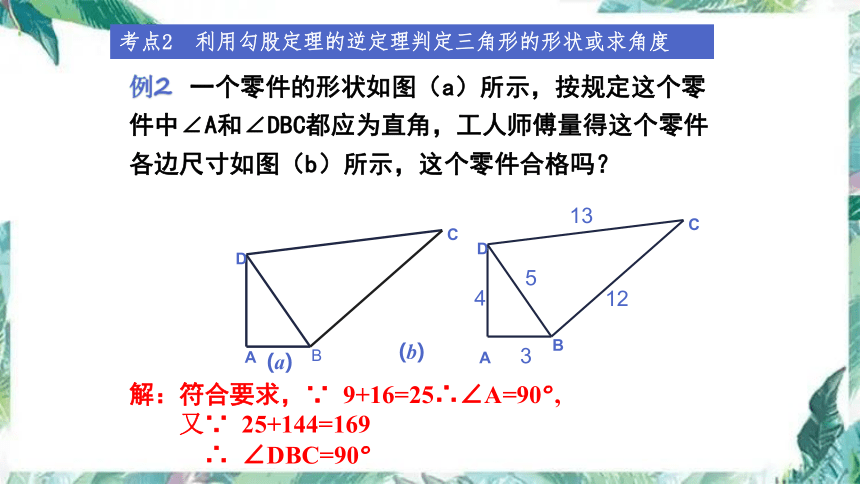
例2 一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
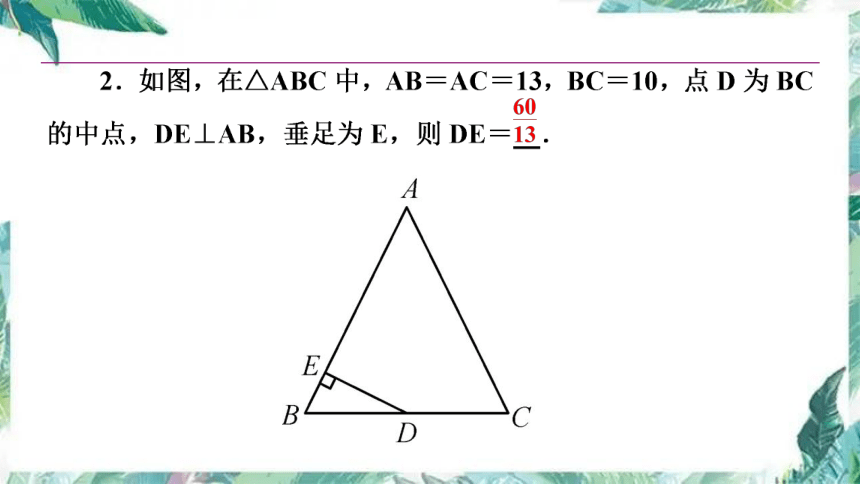
A
B
C
D
3
4
5
12
13
(a)
(b)
解:符合要求,∵ 9+16=25∴∠A=90°,
又∵ 25+144=169
∴ ∠DBC=90°
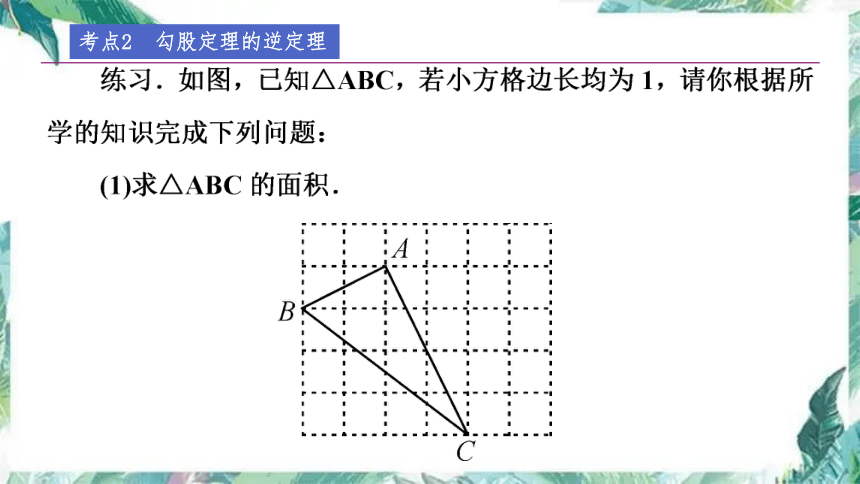
考点2 勾股定理的逆定理
例3 在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
8 米
6米
考点3 勾股定理的应用
8 米
6米
A
C
B
解:根据题意可以构建一直角三角形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
由勾股定理得
∴这棵树在折断之前的高度是10+6=16(米).
针对训练
1.假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们在点A登陆后先 往东走8 km到达C处,又往北走了2 km,遇到障 碍后又往西走了3 km,再往北走了6 km后往东拐,仅走了 1km就找到了藏宝点B,如图,登陆点A到藏宝点B的距离是________.
10km
15
02 易错题集训
C
234或126
03 河南常考题型演练
B
A
回顾与思考
勾股定理
课堂小结
勾股定理的应用
勾股的逆定理
感谢聆听!
北师大数学八年级上册
第一章 勾股定理
专题复习
如果直角三角形两直角边分别为a,b,斜边为c,
那么
a2 + b2 = c2
即直角三角形两直角边的平方和等于斜边的平方.
在直角三角形中才可以运用
已知Rt ABC的两直角边分别是3和4,则它的斜边是 .
5
勾股定理的应用条件
要点梳理
要点梳理
一、勾股定理
勾股定理的逆定理
如果三角形的三边长a,b,c满足a2 +b2=c2 ,
那么这个三角形是直角三角形.
满足a2 +b2=c2的三个正整数,称为勾股数.
勾股数
二、勾股定理的逆定理与勾股数
三、勾股定理的应用
例1 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的面积.
解:设另一条直角边长是x cm.由勾股定理得:
152+ x2 =172,x2=172-152=289–225=64,
解得 x=±8(负值舍去),
所以另一直角边长为8 cm,
故直角三角形的面积是:
(cm2).
考点1 利用勾股定理求边长及面积
01 考点精讲
C
针对训练
考点2 利用勾股定理的逆定理判定三角形的形状或求角度
例2 一个零件的形状如图(a)所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图(b)所示,这个零件合格吗?
A
B
C
D
A
B
C
D
3
4
5
12
13
(a)
(b)
解:符合要求,∵ 9+16=25∴∠A=90°,
又∵ 25+144=169
∴ ∠DBC=90°
考点2 勾股定理的逆定理
例3 在一次台风的袭击中,小明家房前的一棵大树在离地面6米处断裂,树的顶部落在离树根底部8米处.你能告诉小明这棵树折断之前有多高吗?
8 米
6米
考点3 勾股定理的应用
8 米
6米
A
C
B
解:根据题意可以构建一直角三角形模型,如图.
在Rt△ABC中,
AC=6米,BC=8米,
由勾股定理得
∴这棵树在折断之前的高度是10+6=16(米).
针对训练
1.假期中,小明和同学们到某海岛上去探宝旅游,按照探宝图,他们在点A登陆后先 往东走8 km到达C处,又往北走了2 km,遇到障 碍后又往西走了3 km,再往北走了6 km后往东拐,仅走了 1km就找到了藏宝点B,如图,登陆点A到藏宝点B的距离是________.
10km
15
02 易错题集训
C
234或126
03 河南常考题型演练
B
A
回顾与思考
勾股定理
课堂小结
勾股定理的应用
勾股的逆定理
感谢聆听!
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
