新人教A版数学选择性必修3 6.2.2排列数 同步练习(Word版含解析)
文档属性
| 名称 | 新人教A版数学选择性必修3 6.2.2排列数 同步练习(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 28.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-06 00:00:00 | ||
图片预览


文档简介
6.2.2 排列数
1.( )
A. B. C. D.
2.已知自然数满足则()
A. B. C. D.
3.旅游体验师小李受某旅游网站邀约,决定对甲、乙、丙、丁这四个景区进行体验式旅游,若甲景区不能最先旅游,乙景区和丁景区不能最后旅游,则小李旅游的方法数为()
A. B. C. D.
4.满足不等式的的最小值为()
A. B. C. D.
5. 由数字组成的无重复数字的位数中,比大的数的个数为( )
A. B. C. D.
6.受新冠肺炎疫情影响,某学校按上级文件指示,要求错峰放学,错峰有序吃饭.高三年级一层楼六个班排队,甲班必须排在前三位,且丙班、丁班必须排在一起,则这六个班排队吃饭的不同安排方案共有( )
A.种 B.种 C.种 D.种
7.现要把盆不同的兰花和盆不同的玫瑰花摆放在图中的位置上,其中盆兰花不能摆在一条直线上,则不同的摆放方法有( )
A.种 B.种 C.种 D.种
8.中国古代的五音,一般指五声音阶,依次为宫、商、角、徵、羽.如果把这五个音阶全用上,排成一个五个音阶的音序,且要求宫、羽两音阶在角音阶的同侧,可排成的不同音序的种数为( )
A. B. C. D.
9.若则的值为 .
10.计算 .
11.名老党员在建军节这天相约来到革命圣地之一的西柏坡追忆抗战生活名老党员中有名党员当年在同一个班,他们站成一排拍照留念时,要求同班的名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片为元(不含过塑费),且有一半的照片需要过塑,每张照片的过塑费为元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为 .
12.某项化学实验中,要把种甲类物质和种乙类物质按照先放甲类物质后放乙类物质的顺序(甲类物质和乙类物质也分别有顺序)依次放入某种液体中,观察反应结果.现有符合条件的种甲类物质和种乙类物质可供使用,为了能得到所有的实验结果,这个实验一共要进行 次.
13.从名运动员中选出人参加接力赛,分别求满足下列条件的安排方法种数:
(1)甲、乙都不跑中间两棒;
(2)甲、乙不都跑中间两棒.
14.某高校从某系的 名优秀毕业生中选 人分别到西部的座城市参加中国西部经济开发建设,其中甲同学不到城,乙同学不到城,共有多少种不同的派遣方案?
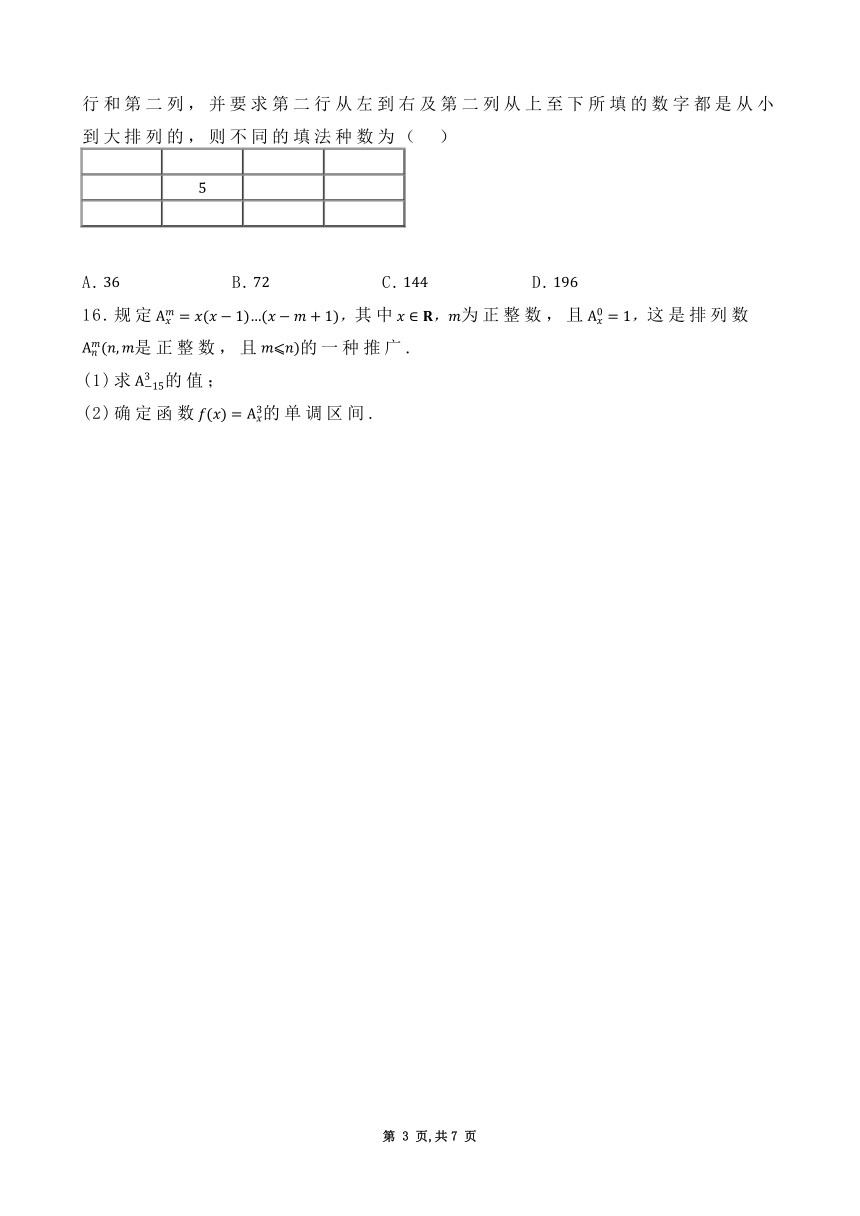
15.“数独九宫格”原创者是世纪的瑞士数学家欧拉,它的游戏规则很简单,将到这九个自然数填到如图所示的小九宫格的个空格里,每个空格填一个数,且个空格的数字各不相同.若中间空格已填数字且只填第二行和第二列,并要求第二行从左到右及第二列从上至下所填的数字都是从小到大排列的,则不同的填法种数为( )
A. B. C. D.
16.规定其中为正整数,且这是排列数是正整数,且的一种推广.
(1)求的值;
(2)确定函数的单调区间.
参考答案
1.【答案】:A
【解析】:.故选A.
2.【答案】:C
【解析】:自然数满足
,
整理得解得或(舍).
3.【答案】:D
【解析】:若甲景区最后旅游,则乙、丙、丁三个景区任意排,故有(种), 若甲景区不最后旅游,则丙景区最后旅游,故有(种), 根据分类加法计数原理,共有(种)旅游方法, 故选D.
4.【答案】:B
【解析】:由排列数公式得即解得或又所以.又所以的最小值为.故选B.
5.【答案】:B
【解析】:根据题意,分种情况讨论:
当首位为时,将剩下的三个数字全排列,安排在后面的三个数位,有种情况,即有个符合条件的位数;
,当首位为时,
若百位为或时,将剩下的两个数字全排列,安排在后面的两个数位,有种情况,即有个符合条件的位数;
若首位为,百位为时,只有一个符合条件的位数;
综上共有个符合条件的位数;
故选B.
6.【答案】:B
【解析】:根据题意,甲班必须排在前三位,分三种情况讨论:
①甲班排在第一位,丙班、丁班排在一起的情况有(种),将剩余的三个班级全排列,安排到剩下的三个位置,有(种)情况,此时有(种)安排方案;
②甲班排在第二位,丙班、丁班排在一起的情况有(种),将剩余的三个班级全排列,安排到剩下的三个位置,有(种)情况,此时有(种)安排方案;
③甲班排在第三位,丙班、丁班排在一起的情况有(种),将剩余的三个班级全排列,安排到剩下的三个位置,有(种)情况,此时有(种)安排方案.
故一共有(种)安排方案.故选B.
7.【答案】:B
【解析】:将盆花全排列共有种摆法,其中盆兰花摆在一条直线上的摆法有种, 故共有(种)不同摆法.
8.【答案】:C
【解析】:由题意,可看作五个位置排列五种事物. 若角音阶排在第一位,则宫、羽两音阶可以排在第二~五个位置当中的任意位置,共有(种)排法; 若角音阶排在第二位,则宫、羽两音阶可以排在第三~五个位置当中的任意位置,共有(种)排法; 若角音阶排在第三位,则宫、羽两音阶可以排在第一、二个位置或第四、五个位置当中的任意位置,共有(种)排法; 若角音阶排在第四位,则宫、羽两音阶可以排在第一~三个位置当中的任意位置,共有(种)排法; 若角音阶排在第五位,则宫、羽两音阶可以排在第一~四个位置当中的任意位置,共有(种)排法. 共有(种)排法,即有种不同的音序,故选C.
9.【答案】:
【解析】:由得
解得(舍去)或.
10.【答案】:
【解析】:
11.【答案】:元
【解析】:利用捆绑法可求得照片的总张数为则每名老党员需要支付的照片费为(元).
12.【答案】:
【解析】:根据题意,由于要把种甲类物质和种乙类物质按照先放甲类物质后放乙类物质的顺序依次放入某种液体中,分步进行分析:第步,放入甲类物质,从种甲类物质选出种,共有种方案;第步,放入乙类物质,从种乙类物质选出种,共有种方案.根据分步乘法计数原理,共有(种)方案.因此,共要进行次实验,才能得到所有的实验结果.
13
(1)【答案】先选跑中间两棒的人,有(种)安排方法,再从余下的人中选人跑第一、四棒,有(种)安排方法,则共有(种)安排方法.
(2)【答案】用间接法:“不都跑”的否定是“都跑”,所以选人任意排有(种)方法,甲、乙跑中间两棒的安排方法有(种),故共有(种)安排方法.
14.【答案】:因为甲、乙有限制条件,所以按照派遣人员中是否有甲、乙来分类,有以下 种情况:
①若甲、乙都不参加,则派遣方案有种;
②若甲参加而乙不参加,先安排甲,有 种方案,然后安排其余人,有 种方案,所以共有 种方案;
③若乙参加而甲不参加,也有 种方案;
④若甲、乙都参加,则先安排甲、乙,有 种方案,然后再安排其余 人中的 人到另外两个城市,有 种方案,所以共有 种方案.
所以不同的派遣方案共有(种).
15.【答案】:C
【解析】:根据题意,如图,假设第二行的两个空格为第二列的两个空格为.分两步进行分析:①对于空格需要在四个数字中任选两个,有(种)选法;②对于空格需要在四个数字中任选两个,有(种)选法.则有(种)不同的填法,故选C.
16
(1)【答案】由已知得.
(2)【答案】函数
则.
令得或
所以函数的单调递增区间为;
令得
所以函数的单调递减区间为.
第 7 页,共7 页
1.( )
A. B. C. D.
2.已知自然数满足则()
A. B. C. D.
3.旅游体验师小李受某旅游网站邀约,决定对甲、乙、丙、丁这四个景区进行体验式旅游,若甲景区不能最先旅游,乙景区和丁景区不能最后旅游,则小李旅游的方法数为()
A. B. C. D.
4.满足不等式的的最小值为()
A. B. C. D.
5. 由数字组成的无重复数字的位数中,比大的数的个数为( )
A. B. C. D.
6.受新冠肺炎疫情影响,某学校按上级文件指示,要求错峰放学,错峰有序吃饭.高三年级一层楼六个班排队,甲班必须排在前三位,且丙班、丁班必须排在一起,则这六个班排队吃饭的不同安排方案共有( )
A.种 B.种 C.种 D.种
7.现要把盆不同的兰花和盆不同的玫瑰花摆放在图中的位置上,其中盆兰花不能摆在一条直线上,则不同的摆放方法有( )
A.种 B.种 C.种 D.种
8.中国古代的五音,一般指五声音阶,依次为宫、商、角、徵、羽.如果把这五个音阶全用上,排成一个五个音阶的音序,且要求宫、羽两音阶在角音阶的同侧,可排成的不同音序的种数为( )
A. B. C. D.
9.若则的值为 .
10.计算 .
11.名老党员在建军节这天相约来到革命圣地之一的西柏坡追忆抗战生活名老党员中有名党员当年在同一个班,他们站成一排拍照留念时,要求同班的名党员站在一起,且满足条件的每种排法都要拍一张照片,若将照片洗出来,每张照片为元(不含过塑费),且有一半的照片需要过塑,每张照片的过塑费为元.若将这些照片平均分给每名老党员(过塑的照片也要平均分),则每名老党员需要支付的照片费为 .
12.某项化学实验中,要把种甲类物质和种乙类物质按照先放甲类物质后放乙类物质的顺序(甲类物质和乙类物质也分别有顺序)依次放入某种液体中,观察反应结果.现有符合条件的种甲类物质和种乙类物质可供使用,为了能得到所有的实验结果,这个实验一共要进行 次.
13.从名运动员中选出人参加接力赛,分别求满足下列条件的安排方法种数:
(1)甲、乙都不跑中间两棒;
(2)甲、乙不都跑中间两棒.
14.某高校从某系的 名优秀毕业生中选 人分别到西部的座城市参加中国西部经济开发建设,其中甲同学不到城,乙同学不到城,共有多少种不同的派遣方案?
15.“数独九宫格”原创者是世纪的瑞士数学家欧拉,它的游戏规则很简单,将到这九个自然数填到如图所示的小九宫格的个空格里,每个空格填一个数,且个空格的数字各不相同.若中间空格已填数字且只填第二行和第二列,并要求第二行从左到右及第二列从上至下所填的数字都是从小到大排列的,则不同的填法种数为( )
A. B. C. D.
16.规定其中为正整数,且这是排列数是正整数,且的一种推广.
(1)求的值;
(2)确定函数的单调区间.
参考答案
1.【答案】:A
【解析】:.故选A.
2.【答案】:C
【解析】:自然数满足
,
整理得解得或(舍).
3.【答案】:D
【解析】:若甲景区最后旅游,则乙、丙、丁三个景区任意排,故有(种), 若甲景区不最后旅游,则丙景区最后旅游,故有(种), 根据分类加法计数原理,共有(种)旅游方法, 故选D.
4.【答案】:B
【解析】:由排列数公式得即解得或又所以.又所以的最小值为.故选B.
5.【答案】:B
【解析】:根据题意,分种情况讨论:
当首位为时,将剩下的三个数字全排列,安排在后面的三个数位,有种情况,即有个符合条件的位数;
,当首位为时,
若百位为或时,将剩下的两个数字全排列,安排在后面的两个数位,有种情况,即有个符合条件的位数;
若首位为,百位为时,只有一个符合条件的位数;
综上共有个符合条件的位数;
故选B.
6.【答案】:B
【解析】:根据题意,甲班必须排在前三位,分三种情况讨论:
①甲班排在第一位,丙班、丁班排在一起的情况有(种),将剩余的三个班级全排列,安排到剩下的三个位置,有(种)情况,此时有(种)安排方案;
②甲班排在第二位,丙班、丁班排在一起的情况有(种),将剩余的三个班级全排列,安排到剩下的三个位置,有(种)情况,此时有(种)安排方案;
③甲班排在第三位,丙班、丁班排在一起的情况有(种),将剩余的三个班级全排列,安排到剩下的三个位置,有(种)情况,此时有(种)安排方案.
故一共有(种)安排方案.故选B.
7.【答案】:B
【解析】:将盆花全排列共有种摆法,其中盆兰花摆在一条直线上的摆法有种, 故共有(种)不同摆法.
8.【答案】:C
【解析】:由题意,可看作五个位置排列五种事物. 若角音阶排在第一位,则宫、羽两音阶可以排在第二~五个位置当中的任意位置,共有(种)排法; 若角音阶排在第二位,则宫、羽两音阶可以排在第三~五个位置当中的任意位置,共有(种)排法; 若角音阶排在第三位,则宫、羽两音阶可以排在第一、二个位置或第四、五个位置当中的任意位置,共有(种)排法; 若角音阶排在第四位,则宫、羽两音阶可以排在第一~三个位置当中的任意位置,共有(种)排法; 若角音阶排在第五位,则宫、羽两音阶可以排在第一~四个位置当中的任意位置,共有(种)排法. 共有(种)排法,即有种不同的音序,故选C.
9.【答案】:
【解析】:由得
解得(舍去)或.
10.【答案】:
【解析】:
11.【答案】:元
【解析】:利用捆绑法可求得照片的总张数为则每名老党员需要支付的照片费为(元).
12.【答案】:
【解析】:根据题意,由于要把种甲类物质和种乙类物质按照先放甲类物质后放乙类物质的顺序依次放入某种液体中,分步进行分析:第步,放入甲类物质,从种甲类物质选出种,共有种方案;第步,放入乙类物质,从种乙类物质选出种,共有种方案.根据分步乘法计数原理,共有(种)方案.因此,共要进行次实验,才能得到所有的实验结果.
13
(1)【答案】先选跑中间两棒的人,有(种)安排方法,再从余下的人中选人跑第一、四棒,有(种)安排方法,则共有(种)安排方法.
(2)【答案】用间接法:“不都跑”的否定是“都跑”,所以选人任意排有(种)方法,甲、乙跑中间两棒的安排方法有(种),故共有(种)安排方法.
14.【答案】:因为甲、乙有限制条件,所以按照派遣人员中是否有甲、乙来分类,有以下 种情况:
①若甲、乙都不参加,则派遣方案有种;
②若甲参加而乙不参加,先安排甲,有 种方案,然后安排其余人,有 种方案,所以共有 种方案;
③若乙参加而甲不参加,也有 种方案;
④若甲、乙都参加,则先安排甲、乙,有 种方案,然后再安排其余 人中的 人到另外两个城市,有 种方案,所以共有 种方案.
所以不同的派遣方案共有(种).
15.【答案】:C
【解析】:根据题意,如图,假设第二行的两个空格为第二列的两个空格为.分两步进行分析:①对于空格需要在四个数字中任选两个,有(种)选法;②对于空格需要在四个数字中任选两个,有(种)选法.则有(种)不同的填法,故选C.
16
(1)【答案】由已知得.
(2)【答案】函数
则.
令得或
所以函数的单调递增区间为;
令得
所以函数的单调递减区间为.
第 7 页,共7 页
