2022—2023学年人教版数学八年级下册 第18章平行四边形 综合性练习(word、含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册 第18章平行四边形 综合性练习(word、含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 672.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 07:02:25 | ||
图片预览



文档简介
八下_第18章平行四边形_综合性练习
一、选择题(共9小题)
1. 如图,点 是矩形 的边 延长线上的一点,且 ,连接 交 于点 ,连接 ,则下列结论不正确的是
A. B.
C. D.
2. 在平行四边形 中,对角线 , 相交于点 ,,,则 的取值范围是
A. B. C. D.
3. 在 中,, 于 , 为 的中点,,则 的长为
A. B. C. D.
4. 已知菱形的边长为 ,一个内角为 ,则该菱形较长的对角线的长是
A. B. C. D.
5. 如图,在菱形 中,,,则对角线 的长等于
A. B. C. D.
6. 如图,将边长为 的正方形纸片 折叠,使点 落在 边的中点 处,点 落在点 处,折痕为 ,则线段 的长是
A. B. C. D.
7. 在平行四边形 中,,那么下列各式中,不能成立的是
A. B.
C. D.
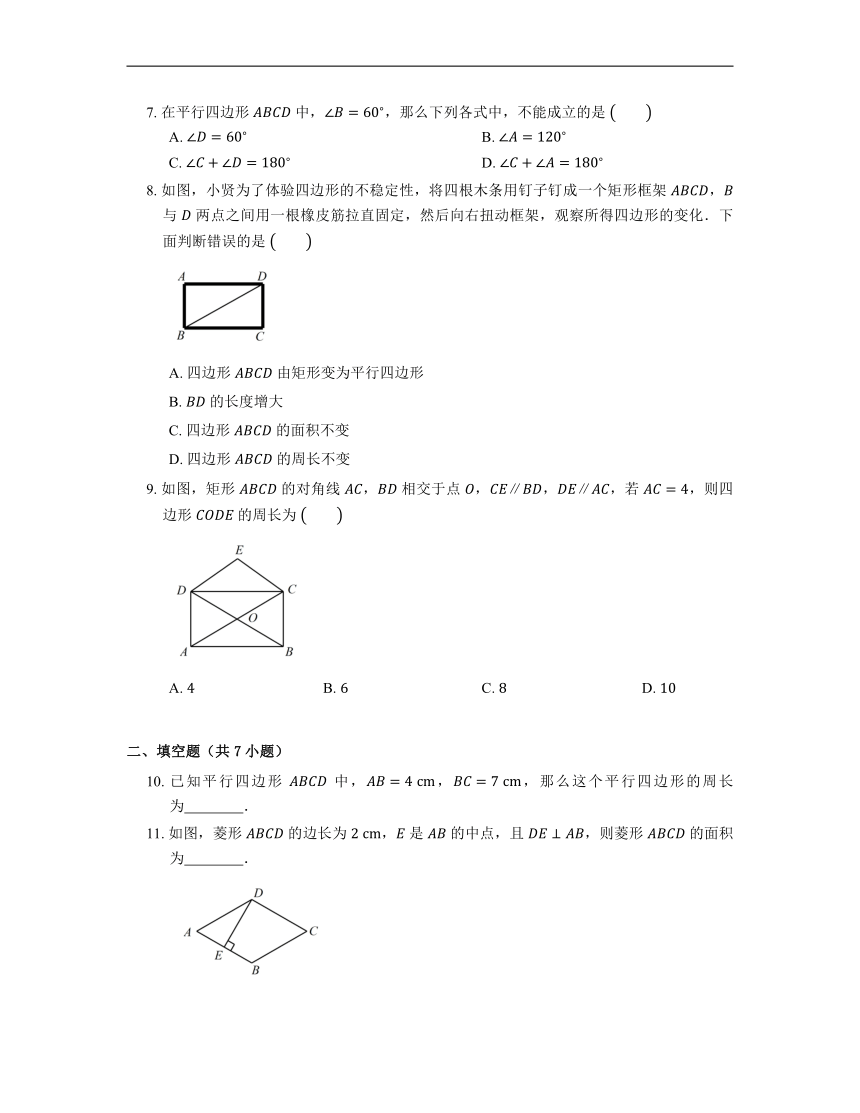
8. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架 , 与 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化.下面判断错误的是
A. 四边形 由矩形变为平行四边形
B. 的长度增大
C. 四边形 的面积不变
D. 四边形 的周长不变
9. 如图,矩形 的对角线 , 相交于点 ,,,若 ,则四边形 的周长为
A. B. C. D.
二、填空题(共7小题)
10. 已知平行四边形 中,,,那么这个平行四边形的周长为 .
11. 如图,菱形 的边长为 , 是 的中点,且 ,则菱形 的面积为 .
12. 在矩形 中,对角线 , 相交于点 ,,垂足为 ,如果 ,,那么 .
13. 如图,在正方形 中,点 为 上一点, 与 相交于点 ,若 ,则 等于 度.
14. 如图,过矩形 的对角线 上一点 ,分别作矩形两边的平行线 与 ,那么图中矩形 的面积 与矩形 的面积 的大小关系是 .(填“”“”或“”)
15. 如图,四边形 是矩形纸片,.对折矩形纸片 ,使 与 重合,折痕为 ;展平后再过点 折叠矩形纸片,使点 落在 上的点 处,折痕 与 相交于点 ;再次展平,连接 ,,延长 交 于点 .有如下结论:① ;② ;③ ;④ 是等边三角形;⑤ 为线段 上一动点, 是 的中点,则 的最小值是 .其中正确结论的序号是 .
16. 如图,矩形 中,,, 为 上一点,将 沿 翻折至 , 与 相交于点 ,且 ,则 的长为 .
三、解答题(共7小题)
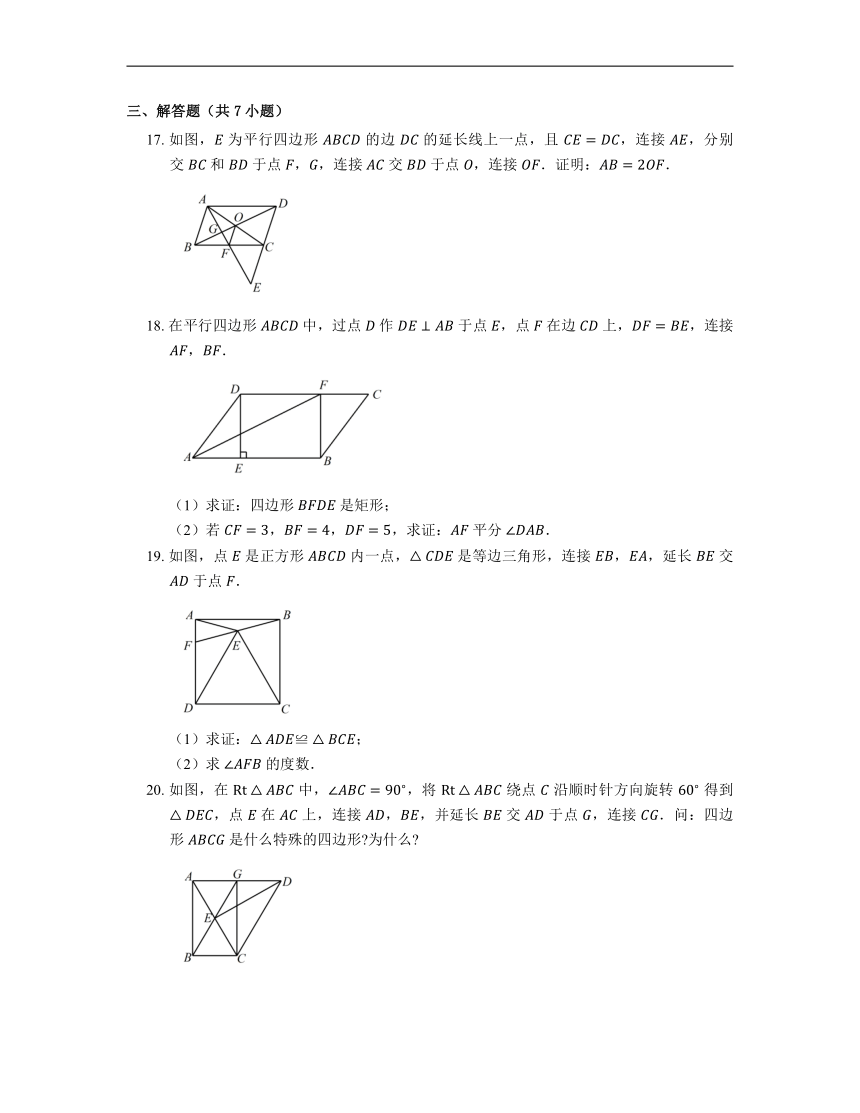
17. 如图, 为平行四边形 的边 的延长线上一点,且 ,连接 ,分别交 和 于点 ,,连接 交 于点 ,连接 .证明:.
18. 在平行四边形 中,过点 作 于点 ,点 在边 上,,连接 ,.
(1)求证:四边形 是矩形;
(2)若 ,,,求证: 平分 .
19. 如图,点 是正方形 内一点, 是等边三角形,连接 ,,延长 交 于点 .
(1)求证:;
(2)求 的度数.
20. 如图,在 中,,将 绕点 沿顺时针方向旋转 得到 ,点 在 上,连接 ,,并延长 交 于点 ,连接 .问:四边形 是什么特殊的四边形 为什么
21. 如图所示,平行四边形 中,,,, 是 的中点, 是边 上的动点, 的延长线与 的延长线交于点 ,连接 ,.
(1)求证:四边形 是平行四边形.
(2)①当 时,四边形 是矩形.
②当 时,四边形 时菱形.(直接写出答案,不需要说明理由)
22. 如图,在 中,, 是 的一个外角,
实践与操作:根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).
(1)作 的平分线 ;
(2)作线段 的垂直平分线,与 交于点 ,与 边交于点 ,连接 ,.
猜想并证明:判断四边形 的形状并加以证明.
23. 完成下列问题.
(1)如图①,纸片平行四边形 中,,.过点 作 ,垂足为 ,沿 剪下 ,将它平移至 的位置,拼成四边形 ,则四边形 的形状为()
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图②,在(1)中的四边形纸片 中,在 上取一点 ,使 ,剪下 ,将它平移至 的位置,拼成四边形 .
①求证:四边形 是菱形;
②求:四边形 的两条对角线的长.
答案
1. A
2. D
3. B
4. B
5. D
6. B
7. D
8. C
【解析】 向右扭动框架,矩形变为平行四边形,底长不变,高变小,
所以面积变小.
9. C
10.
11.
12.
13.
【解析】由题易知 ,,
因为在 与 中,
所以 ,
所以 ,.
因为 ,
所以 ,
所以 .
14.
【解析】由矩形的特征可知,矩形的一条对角线把矩形分成面积相等的两个三角形,即 ,,,
所以 .
15. ①④⑤
16.
【解析】
四边形 是矩形,
,,,
根据题意得:,
,,,
在 和 中,
(),
,,
.
设 ,则 ,,
,,
根据勾股定理得:,
即 ,解得:.
.
17. 四边形 为平行四边形,
,,
,,
又 ,
,
.
点 为 , 的交点,
为 的中位线,
,,即 .
18. (1) 四边形 是平行四边形,
.
,
四边形 是平行四边形.
,
.
四边形 是矩形.
(2) ,, ,
由勾股定理,得 .
.
,
.
平分 .
19. (1) 因为四边形 是正方形, 是等边三角形,
所以 ,,,,
所以 ,
所以 .
(2) 由题易知 ,,
所以 ,
因为 ,
所以 .
20. 四边形 是矩形.
理由:
是由 绕点 顺时针旋转 得到的,
,,,
是等边三角形,
,又 ,
,
.
, 为正三角形,
,
又 ,
,
,
四边形 是平行四边形.
又 ,
四边形 是矩形.
21. (1) 四边形 是平行四边形,
,
.
是 的中点,
.
在 和 中,
.
.
,
四边形 是平行四边形.
(2) ;
22. (1) 如图 所示, 即为所求.
(2) 作图如图 所示.
猜想:四边形 是菱形.
证明:
, 平分 ,
,,
是 的外角,
,
,
,
,
垂直平分 ,
,,
在 和 中,
,
,
在四边形 中,,,
四边形 是平行四边形,
,
四边形 是菱形.
23. (1) C
(2) 平移到 ,
四边形 是平行四边形.
,,,
.
,
,
,
四边形 是菱形
连接 ,.
在 中,
,,
.
在 中,
,,
一、选择题(共9小题)
1. 如图,点 是矩形 的边 延长线上的一点,且 ,连接 交 于点 ,连接 ,则下列结论不正确的是
A. B.
C. D.
2. 在平行四边形 中,对角线 , 相交于点 ,,,则 的取值范围是
A. B. C. D.
3. 在 中,, 于 , 为 的中点,,则 的长为
A. B. C. D.
4. 已知菱形的边长为 ,一个内角为 ,则该菱形较长的对角线的长是
A. B. C. D.
5. 如图,在菱形 中,,,则对角线 的长等于
A. B. C. D.
6. 如图,将边长为 的正方形纸片 折叠,使点 落在 边的中点 处,点 落在点 处,折痕为 ,则线段 的长是
A. B. C. D.
7. 在平行四边形 中,,那么下列各式中,不能成立的是
A. B.
C. D.
8. 如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架 , 与 两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化.下面判断错误的是
A. 四边形 由矩形变为平行四边形
B. 的长度增大
C. 四边形 的面积不变
D. 四边形 的周长不变
9. 如图,矩形 的对角线 , 相交于点 ,,,若 ,则四边形 的周长为
A. B. C. D.
二、填空题(共7小题)
10. 已知平行四边形 中,,,那么这个平行四边形的周长为 .
11. 如图,菱形 的边长为 , 是 的中点,且 ,则菱形 的面积为 .
12. 在矩形 中,对角线 , 相交于点 ,,垂足为 ,如果 ,,那么 .
13. 如图,在正方形 中,点 为 上一点, 与 相交于点 ,若 ,则 等于 度.
14. 如图,过矩形 的对角线 上一点 ,分别作矩形两边的平行线 与 ,那么图中矩形 的面积 与矩形 的面积 的大小关系是 .(填“”“”或“”)
15. 如图,四边形 是矩形纸片,.对折矩形纸片 ,使 与 重合,折痕为 ;展平后再过点 折叠矩形纸片,使点 落在 上的点 处,折痕 与 相交于点 ;再次展平,连接 ,,延长 交 于点 .有如下结论:① ;② ;③ ;④ 是等边三角形;⑤ 为线段 上一动点, 是 的中点,则 的最小值是 .其中正确结论的序号是 .
16. 如图,矩形 中,,, 为 上一点,将 沿 翻折至 , 与 相交于点 ,且 ,则 的长为 .
三、解答题(共7小题)
17. 如图, 为平行四边形 的边 的延长线上一点,且 ,连接 ,分别交 和 于点 ,,连接 交 于点 ,连接 .证明:.
18. 在平行四边形 中,过点 作 于点 ,点 在边 上,,连接 ,.
(1)求证:四边形 是矩形;
(2)若 ,,,求证: 平分 .
19. 如图,点 是正方形 内一点, 是等边三角形,连接 ,,延长 交 于点 .
(1)求证:;
(2)求 的度数.
20. 如图,在 中,,将 绕点 沿顺时针方向旋转 得到 ,点 在 上,连接 ,,并延长 交 于点 ,连接 .问:四边形 是什么特殊的四边形 为什么
21. 如图所示,平行四边形 中,,,, 是 的中点, 是边 上的动点, 的延长线与 的延长线交于点 ,连接 ,.
(1)求证:四边形 是平行四边形.
(2)①当 时,四边形 是矩形.
②当 时,四边形 时菱形.(直接写出答案,不需要说明理由)
22. 如图,在 中,, 是 的一个外角,
实践与操作:根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).
(1)作 的平分线 ;
(2)作线段 的垂直平分线,与 交于点 ,与 边交于点 ,连接 ,.
猜想并证明:判断四边形 的形状并加以证明.
23. 完成下列问题.
(1)如图①,纸片平行四边形 中,,.过点 作 ,垂足为 ,沿 剪下 ,将它平移至 的位置,拼成四边形 ,则四边形 的形状为()
A.平行四边形 B.菱形 C.矩形 D.正方形
(2)如图②,在(1)中的四边形纸片 中,在 上取一点 ,使 ,剪下 ,将它平移至 的位置,拼成四边形 .
①求证:四边形 是菱形;
②求:四边形 的两条对角线的长.
答案
1. A
2. D
3. B
4. B
5. D
6. B
7. D
8. C
【解析】 向右扭动框架,矩形变为平行四边形,底长不变,高变小,
所以面积变小.
9. C
10.
11.
12.
13.
【解析】由题易知 ,,
因为在 与 中,
所以 ,
所以 ,.
因为 ,
所以 ,
所以 .
14.
【解析】由矩形的特征可知,矩形的一条对角线把矩形分成面积相等的两个三角形,即 ,,,
所以 .
15. ①④⑤
16.
【解析】
四边形 是矩形,
,,,
根据题意得:,
,,,
在 和 中,
(),
,,
.
设 ,则 ,,
,,
根据勾股定理得:,
即 ,解得:.
.
17. 四边形 为平行四边形,
,,
,,
又 ,
,
.
点 为 , 的交点,
为 的中位线,
,,即 .
18. (1) 四边形 是平行四边形,
.
,
四边形 是平行四边形.
,
.
四边形 是矩形.
(2) ,, ,
由勾股定理,得 .
.
,
.
平分 .
19. (1) 因为四边形 是正方形, 是等边三角形,
所以 ,,,,
所以 ,
所以 .
(2) 由题易知 ,,
所以 ,
因为 ,
所以 .
20. 四边形 是矩形.
理由:
是由 绕点 顺时针旋转 得到的,
,,,
是等边三角形,
,又 ,
,
.
, 为正三角形,
,
又 ,
,
,
四边形 是平行四边形.
又 ,
四边形 是矩形.
21. (1) 四边形 是平行四边形,
,
.
是 的中点,
.
在 和 中,
.
.
,
四边形 是平行四边形.
(2) ;
22. (1) 如图 所示, 即为所求.
(2) 作图如图 所示.
猜想:四边形 是菱形.
证明:
, 平分 ,
,,
是 的外角,
,
,
,
,
垂直平分 ,
,,
在 和 中,
,
,
在四边形 中,,,
四边形 是平行四边形,
,
四边形 是菱形.
23. (1) C
(2) 平移到 ,
四边形 是平行四边形.
,,,
.
,
,
,
四边形 是菱形
连接 ,.
在 中,
,,
.
在 中,
,,
