12.3 角的平分线的性质提高卷 2022-2023学年人教版数学八年级上册(Word版含答案)
文档属性
| 名称 | 12.3 角的平分线的性质提高卷 2022-2023学年人教版数学八年级上册(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 631.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览


文档简介
12.3 角的平分线的性质提高卷
一、单选题
1.如图,三条公路两两相交,现计划在△ABC中内部修建一个探照灯,要求探照灯的位置到这三条公路的距离都相等,则探照灯位置是△ABC( )的交点.
A.三条角平分线 B.三条中线
C.三条高的交点 D.三条垂直平分线
2.如图1,已知,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以为圆心,以为半径画弧,分别交射线,于点,;
第二步:分别以,为圆心,以为半径画弧,两弧在内部交于点;
第三步:画射线.射线即为所求.
下列正确的是( )
A.,均无限制 B.,的长
C.有最小限制,无限制 D.,的长
3.如图,在△ABC中,AC=5,AB=7,AD平分∠BAC,DE⊥AC,DE=2,则△ABC的面积为( )
A.14 B.12 C.10 D.7
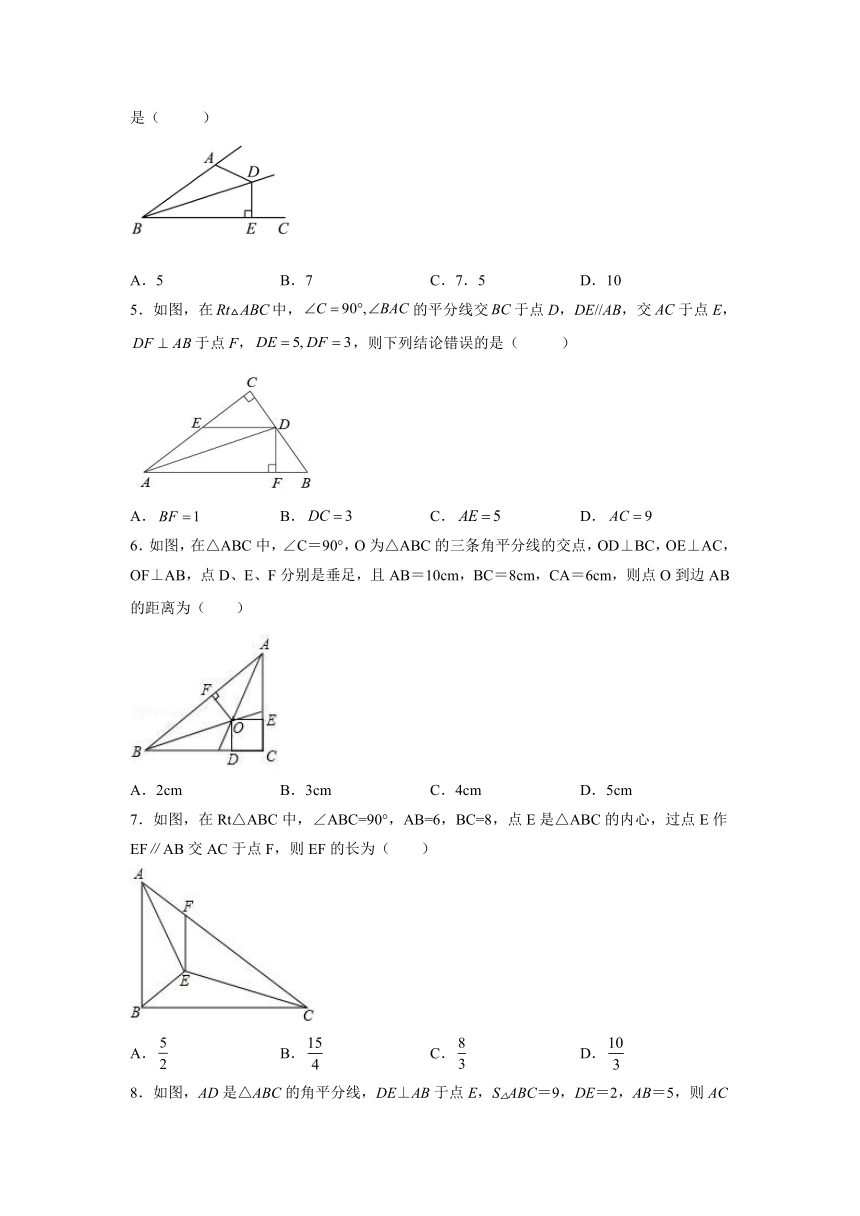
4.如图,为的角平分线,于点,,,则的面积是( )
A.5 B.7 C.7.5 D.10
5.如图,在中,的平分线交于点D,DE//AB,交于点E,于点F,,则下列结论错误的是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到边AB的距离为( )
A.2cm B.3cm C.4cm D.5cm
7.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. B. C. D.
8.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC的长是( )
A.2 B.3 C.4 D.5
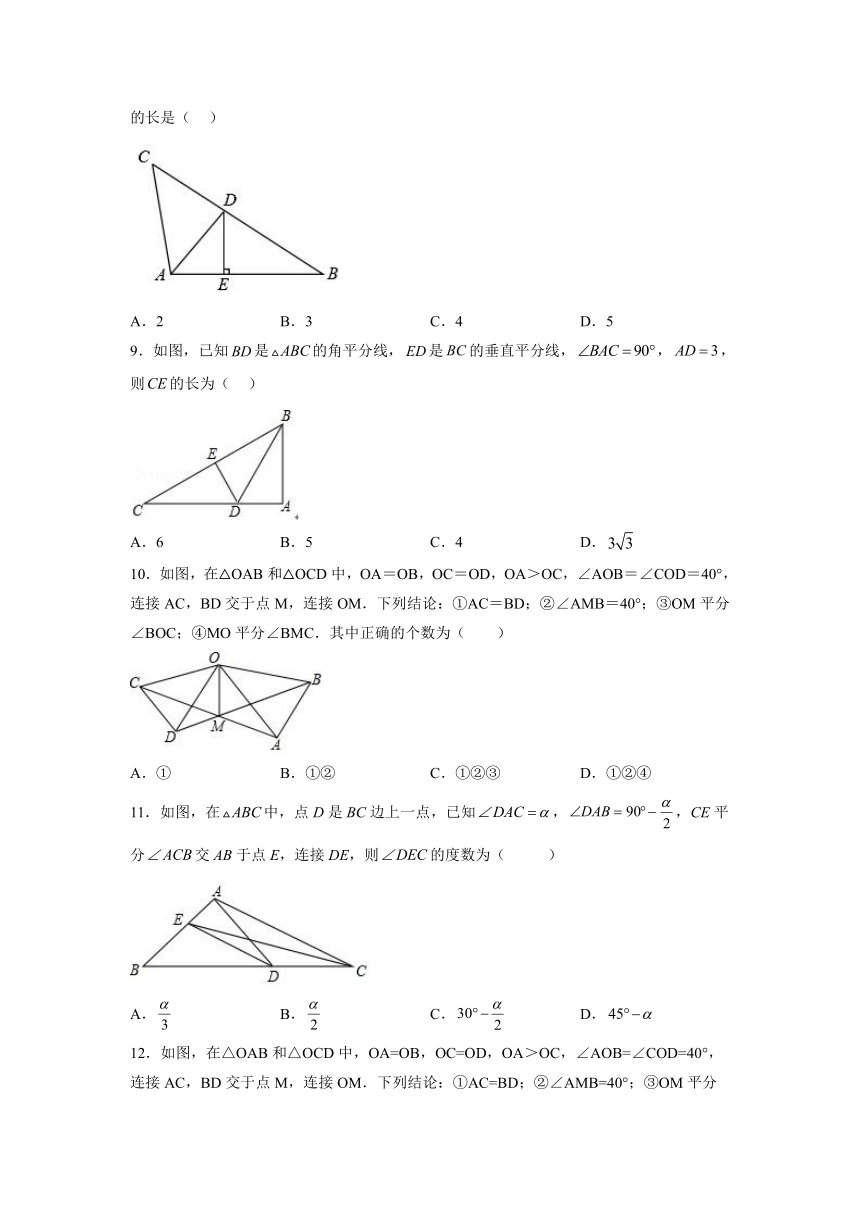
9.如图,已知是的角平分线,是的垂直平分线,,,则的长为( )
A.6 B.5 C.4 D.
10.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.① B.①② C.①②③ D.①②④
11.如图,在中,点D是BC边上一点,已知,,CE平分交AB于点E,连接DE,则的度数为( )
A. B. C. D.
12.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是( )
A.①②④ B.②③④ C.①③④ D.①②③④
二、填空题
13.如图,PM⊥OA,PN⊥OB,∠BOC=30°,PM=PN,则∠AOB=_________.
14.在△ABC中,∠C=90°,AD是△ABC的角平分线,BC=6、AC=8、AB=10,则点D到AB的距离为_______.
15.如图,在中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交AB、BC于点D、E.
②分别以点D、E为圆心,大于的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果,,的面积为18,则的面积为________.
16.如图,,是、的角平分线交点,是、外角平分线交点,则______,_____,联结,则______,点____(选填“在”、“不在”或“不一定在”)直线上.
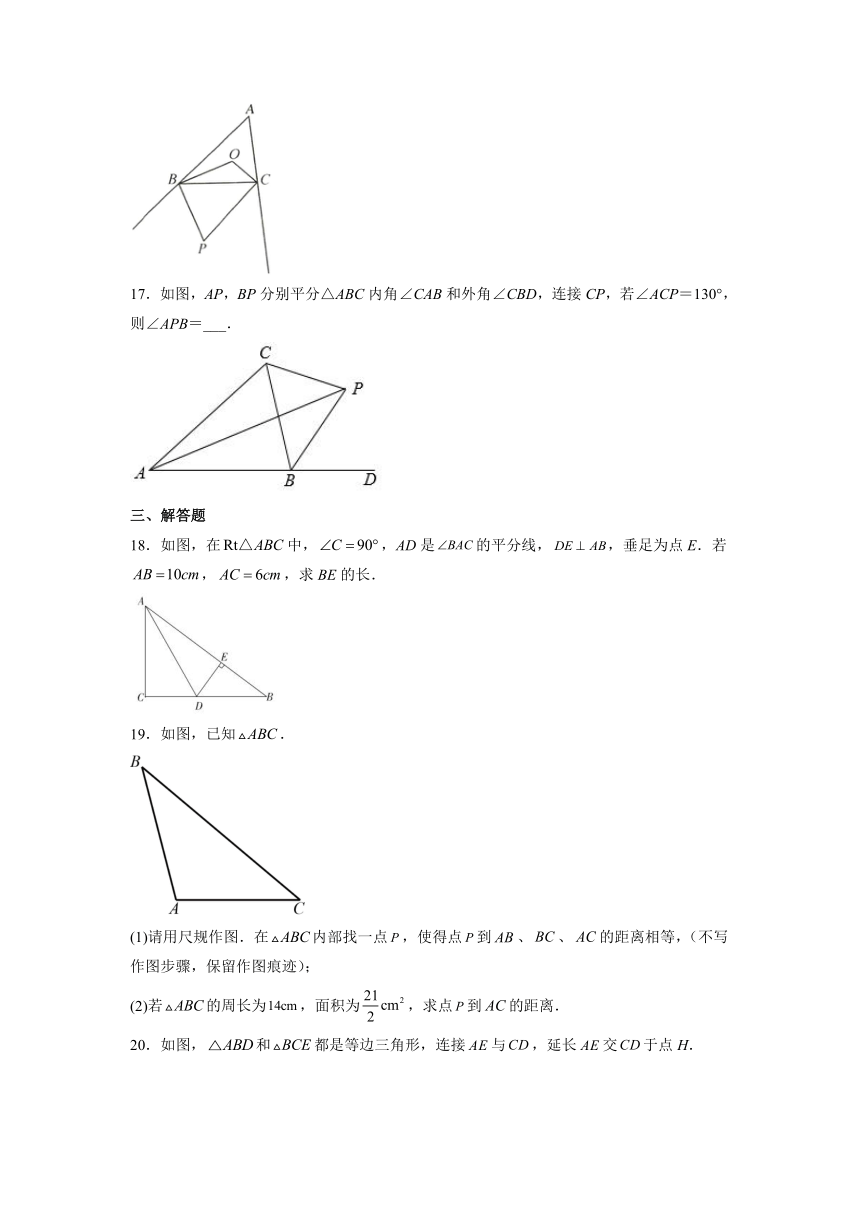
17.如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB=___.
三、解答题
18.如图,在中,,AD是的平分线,,垂足为点E.若,,求BE的长.
19.如图,已知.
(1)请用尺规作图.在内部找一点,使得点到、、的距离相等,(不写作图步骤,保留作图痕迹);
(2)若的周长为,面积为,求点到的距离.
20.如图,和都是等边三角形,连接与,延长交于点H.
(1)证明:;
(2)求的度数;
(3)连接,求证:平分.
21.小明的学习过程中,对教材中的一个有趣问题做如下探究:
(1)【习题回顾】已知:如图1,在中,,是角平分线,是高,相交于点.求证:;
(2)【变式思考】如图2,在中,,是边上的高,若的外角的平分线交的延长线于点,其反向延长线与边的延长线交于点,若,求和的度数;
(3)【探究延伸】如图3,在中,在上存在一点,使得,角平分线交于点.的外角的平分线所在直线与的延长线交于点.若,求的度数.
参考答案
1---10ABBAA AACDD 11--12BA
13.60°
14.#
15.27
16.116 64 26 在
17.
18.解:∵AD是的平分线,,,
∴,
在和中,,
∴≌R(HL),
∴.
∵,,
∴,
∴.
19.(1)
如图,点即为所求,
(2)
设点到的距离为,
由(1)可知点到、、的距离相等
则
解得:
点到的距离为
20.(1)证明:如图1,
∵△ABD和△BCE都是等边三角形,
∴BA=BD,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=60° ∠DBE,
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS),
∴AE=DC.
(2)
解:如图1,由(1)得△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BAD=∠BDA=60°,
∴∠HAD+∠HAD
=∠HAD+∠BDC+∠BDA
=∠HAD+∠BAE+∠BDA
=∠BAD+∠BDA
=120°,
∴∠AHD=180° (∠HAD+∠HDA)=60°.
(3)
证明:如图2,作BF⊥HA于点F,BG⊥HC交HC的延长线于点G,
则∠AFB=∠BFH=∠G=90°,
由△ABE≌△DBC得∠BAF=∠BDG,
在△BAF和△BDG中,
,
∴△BAF≌△BDG(AAS),
∴BF=BG,
∴点B在∠AHC的平分线上,
∴HB平分∠AHC.
21.(1)证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
(2)解:∵∠B=40°,∠ACB=90°,
∴∠GAB=∠B+∠ACB=40°+90°=130°,
∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF130°=65°,
∵CD为AB边上的高,
∴∠ADF=∠ACE=90°,
∴∠CFE=90°﹣∠GAF=90°﹣65°=25°,
又∵∠CAE=∠GAF=65°,∠ACB=90°,
∴∠CEF=90°﹣∠CAE=90°﹣65°=25°;
(3)
证明:∵C、A、G三点共线,AE、AN为角平分线,
∴∠EAN=90°,
又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.
∴∠CFE=90°﹣∠M=90°﹣35°=55°.
一、单选题
1.如图,三条公路两两相交,现计划在△ABC中内部修建一个探照灯,要求探照灯的位置到这三条公路的距离都相等,则探照灯位置是△ABC( )的交点.
A.三条角平分线 B.三条中线
C.三条高的交点 D.三条垂直平分线
2.如图1,已知,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以为圆心,以为半径画弧,分别交射线,于点,;
第二步:分别以,为圆心,以为半径画弧,两弧在内部交于点;
第三步:画射线.射线即为所求.
下列正确的是( )
A.,均无限制 B.,的长
C.有最小限制,无限制 D.,的长
3.如图,在△ABC中,AC=5,AB=7,AD平分∠BAC,DE⊥AC,DE=2,则△ABC的面积为( )
A.14 B.12 C.10 D.7
4.如图,为的角平分线,于点,,,则的面积是( )
A.5 B.7 C.7.5 D.10
5.如图,在中,的平分线交于点D,DE//AB,交于点E,于点F,,则下列结论错误的是( )
A. B. C. D.
6.如图,在△ABC中,∠C=90°,O为△ABC的三条角平分线的交点,OD⊥BC,OE⊥AC,OF⊥AB,点D、E、F分别是垂足,且AB=10cm,BC=8cm,CA=6cm,则点O到边AB的距离为( )
A.2cm B.3cm C.4cm D.5cm
7.如图,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,点E是△ABC的内心,过点E作EF∥AB交AC于点F,则EF的长为( )
A. B. C. D.
8.如图,AD是△ABC的角平分线,DE⊥AB于点E,S△ABC=9,DE=2,AB=5,则AC的长是( )
A.2 B.3 C.4 D.5
9.如图,已知是的角平分线,是的垂直平分线,,,则的长为( )
A.6 B.5 C.4 D.
10.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的个数为( )
A.① B.①② C.①②③ D.①②④
11.如图,在中,点D是BC边上一点,已知,,CE平分交AB于点E,连接DE,则的度数为( )
A. B. C. D.
12.如图,在△OAB和△OCD中,OA=OB,OC=OD,OA>OC,∠AOB=∠COD=40°,连接AC,BD交于点M,连接OM.下列结论:①AC=BD;②∠AMB=40°;③OM平分∠BOC;④MO平分∠BMC.其中正确的是( )
A.①②④ B.②③④ C.①③④ D.①②③④
二、填空题
13.如图,PM⊥OA,PN⊥OB,∠BOC=30°,PM=PN,则∠AOB=_________.
14.在△ABC中,∠C=90°,AD是△ABC的角平分线,BC=6、AC=8、AB=10,则点D到AB的距离为_______.
15.如图,在中,按以下步骤作图:
①以点B为圆心,任意长为半径作弧,分别交AB、BC于点D、E.
②分别以点D、E为圆心,大于的同样长为半径作弧,两弧交于点F.
③作射线BF交AC于点G.
如果,,的面积为18,则的面积为________.
16.如图,,是、的角平分线交点,是、外角平分线交点,则______,_____,联结,则______,点____(选填“在”、“不在”或“不一定在”)直线上.
17.如图,AP,BP分别平分△ABC内角∠CAB和外角∠CBD,连接CP,若∠ACP=130°,则∠APB=___.
三、解答题
18.如图,在中,,AD是的平分线,,垂足为点E.若,,求BE的长.
19.如图,已知.
(1)请用尺规作图.在内部找一点,使得点到、、的距离相等,(不写作图步骤,保留作图痕迹);
(2)若的周长为,面积为,求点到的距离.
20.如图,和都是等边三角形,连接与,延长交于点H.
(1)证明:;
(2)求的度数;
(3)连接,求证:平分.
21.小明的学习过程中,对教材中的一个有趣问题做如下探究:
(1)【习题回顾】已知:如图1,在中,,是角平分线,是高,相交于点.求证:;
(2)【变式思考】如图2,在中,,是边上的高,若的外角的平分线交的延长线于点,其反向延长线与边的延长线交于点,若,求和的度数;
(3)【探究延伸】如图3,在中,在上存在一点,使得,角平分线交于点.的外角的平分线所在直线与的延长线交于点.若,求的度数.
参考答案
1---10ABBAA AACDD 11--12BA
13.60°
14.#
15.27
16.116 64 26 在
17.
18.解:∵AD是的平分线,,,
∴,
在和中,,
∴≌R(HL),
∴.
∵,,
∴,
∴.
19.(1)
如图,点即为所求,
(2)
设点到的距离为,
由(1)可知点到、、的距离相等
则
解得:
点到的距离为
20.(1)证明:如图1,
∵△ABD和△BCE都是等边三角形,
∴BA=BD,BE=BC,∠ABD=∠EBC=60°,
∴∠ABE=∠DBC=60° ∠DBE,
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS),
∴AE=DC.
(2)
解:如图1,由(1)得△ABE≌△DBC,
∴∠BAE=∠BDC,
∵∠BAD=∠BDA=60°,
∴∠HAD+∠HAD
=∠HAD+∠BDC+∠BDA
=∠HAD+∠BAE+∠BDA
=∠BAD+∠BDA
=120°,
∴∠AHD=180° (∠HAD+∠HDA)=60°.
(3)
证明:如图2,作BF⊥HA于点F,BG⊥HC交HC的延长线于点G,
则∠AFB=∠BFH=∠G=90°,
由△ABE≌△DBC得∠BAF=∠BDG,
在△BAF和△BDG中,
,
∴△BAF≌△BDG(AAS),
∴BF=BG,
∴点B在∠AHC的平分线上,
∴HB平分∠AHC.
21.(1)证明:∵∠ACB=90°,CD是高,
∴∠B+∠CAB=90°,∠ACD+∠CAB=90°,
∴∠B=∠ACD,
∵AE是角平分线,
∴∠CAF=∠DAF,
∵∠CFE=∠CAF+∠ACD∠CEF=∠DAF+∠B,
∴∠CEF=∠CFE;
(2)解:∵∠B=40°,∠ACB=90°,
∴∠GAB=∠B+∠ACB=40°+90°=130°,
∵AF为∠BAG的角平分线,
∴∠GAF=∠DAF130°=65°,
∵CD为AB边上的高,
∴∠ADF=∠ACE=90°,
∴∠CFE=90°﹣∠GAF=90°﹣65°=25°,
又∵∠CAE=∠GAF=65°,∠ACB=90°,
∴∠CEF=90°﹣∠CAE=90°﹣65°=25°;
(3)
证明:∵C、A、G三点共线,AE、AN为角平分线,
∴∠EAN=90°,
又∵∠GAN=∠CAM,
∴∠M+∠CEF=90°,
∵∠CEF=∠EAB+∠B,∠CFE=∠EAC+∠ACD,∠ACD=∠B,
∴∠CEF=∠CFE,
∴∠M+∠CFE=90°.
∴∠CFE=90°﹣∠M=90°﹣35°=55°.
