24.2《点和圆、直线和圆的位置关系》课时练习 2022-2023学年人教版九年级数学上册(Word版含答案)
文档属性
| 名称 | 24.2《点和圆、直线和圆的位置关系》课时练习 2022-2023学年人教版九年级数学上册(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 711.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 14:34:04 | ||
图片预览

文档简介
24.2点和圆、直线和圆的位置关系
一、单选题
1.已知⊙O的半径是4,OP=7,则点P与⊙O的位置关系是( ).
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
2.在平面直角坐标系中,以原点O为圆心,4为半径作圆,点P的坐标是(5,5),则点P与⊙O的位置关系是( )
A.点P在⊙O上 B.点P在⊙O内
C.点P在⊙O外 D.点P在⊙O上或在⊙O外
3.在数轴上,点所表示的实数为3,点所表示的实数为,的半径为2.下列说法中不正确的是( )
A.当时,点在上 B.当时,点在内
C.当时,点在内 D.当时,点在外
4.A,B两个点的坐标分别为(3,4),(﹣5,1),以原点O为圆心,5为半径作⊙O,则下列说法正确的是( )
A.点A,点B都在⊙O上 B.点A在⊙O上,点B在⊙O外
C.点A在⊙O内,点B在⊙O上 D.点A,点B都在⊙O外
5.如图,中,于点,点为上的点,,以点为圆心为半径画圆,下列说法错误的是( )
A.点在外 B.点在外
C.点在外 D.点在内
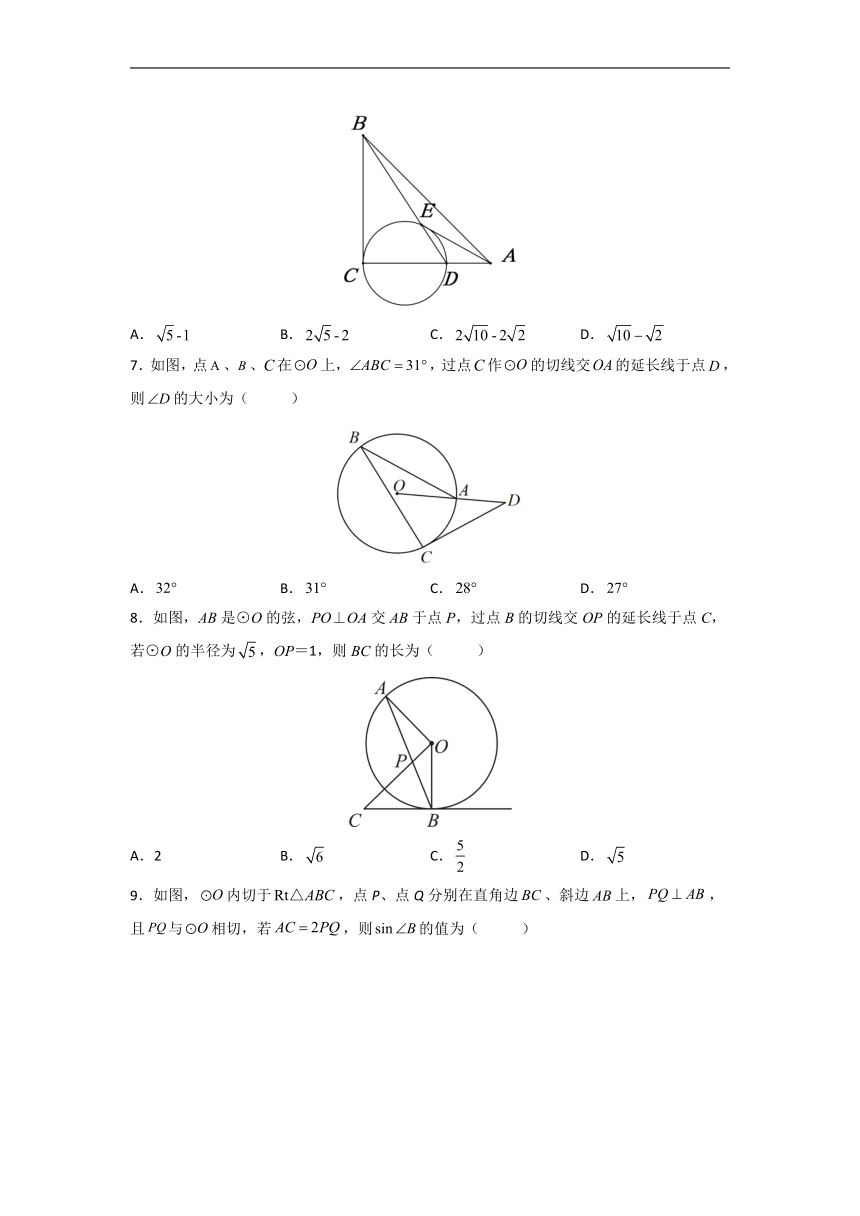
6.如图,△ABC中,∠ACB=90°,AC=BC,点D是边AC上一动点,连接BD,以CD为直径的圆交BD于点E.若AB长为4,则线段AE长的最小值为( )
A. B. C. D.
7.如图,点、、在上,,过点作的切线交的延长线于点,则的大小为( )
A. B. C. D.
8.如图,AB是⊙O的弦,PO⊥OA交AB于点P,过点B的切线交OP的延长线于点C,若⊙O的半径为,OP=1,则BC的长为( )
A.2 B. C. D.
9.如图,内切于,点P、点Q分别在直角边、斜边上,,且与相切,若,则的值为( )
A. B. C. D.
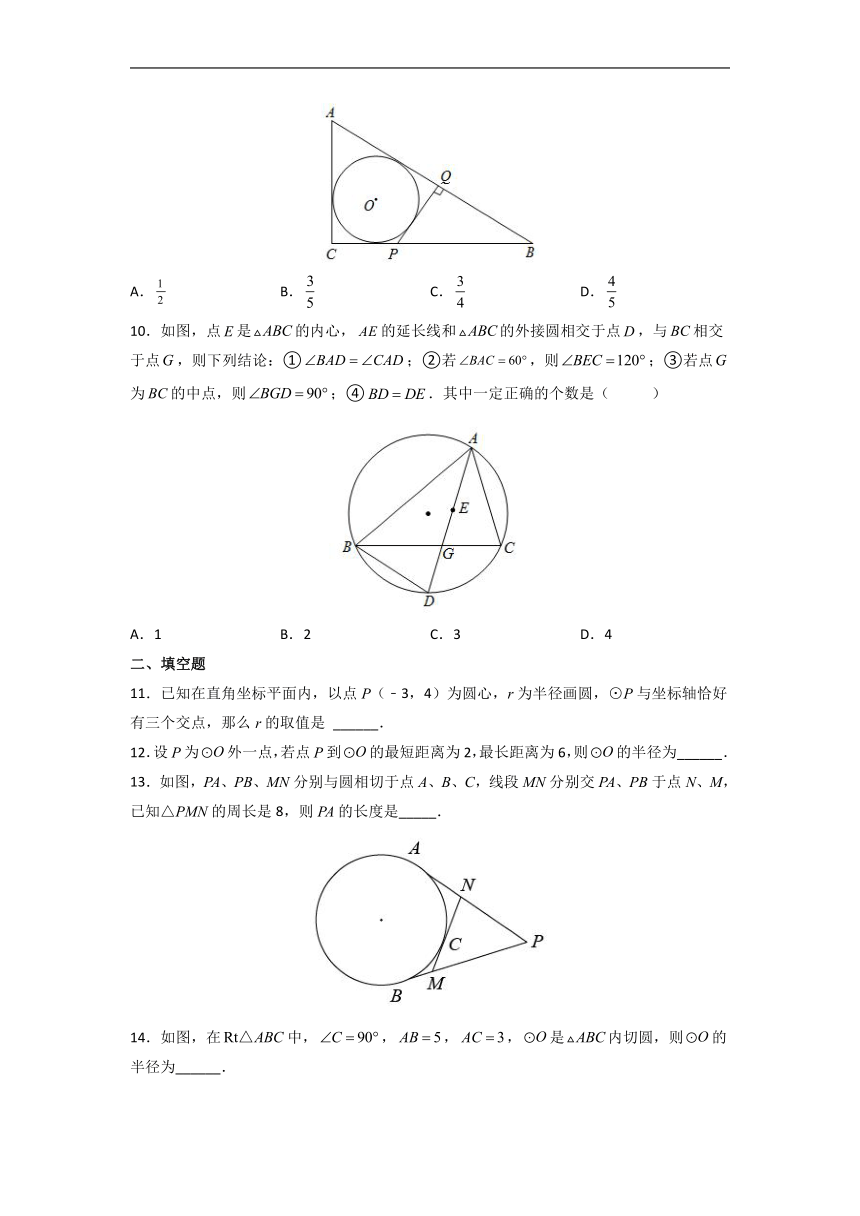
10.如图,点是的内心,的延长线和的外接圆相交于点,与相交于点,则下列结论:①;②若,则;③若点为的中点,则;④.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.已知在直角坐标平面内,以点P(﹣3,4)为圆心,r为半径画圆,⊙P与坐标轴恰好有三个交点,那么r的取值是 ______.
12.设P为外一点,若点P到的最短距离为2,最长距离为6,则的半径为______.
13.如图,PA、PB、MN分别与圆相切于点A、B、C,线段MN分别交PA、PB于点N、M,已知△PMN的周长是8,则PA的长度是_____.
14.如图,在中,,,,是内切圆,则的半径为______.
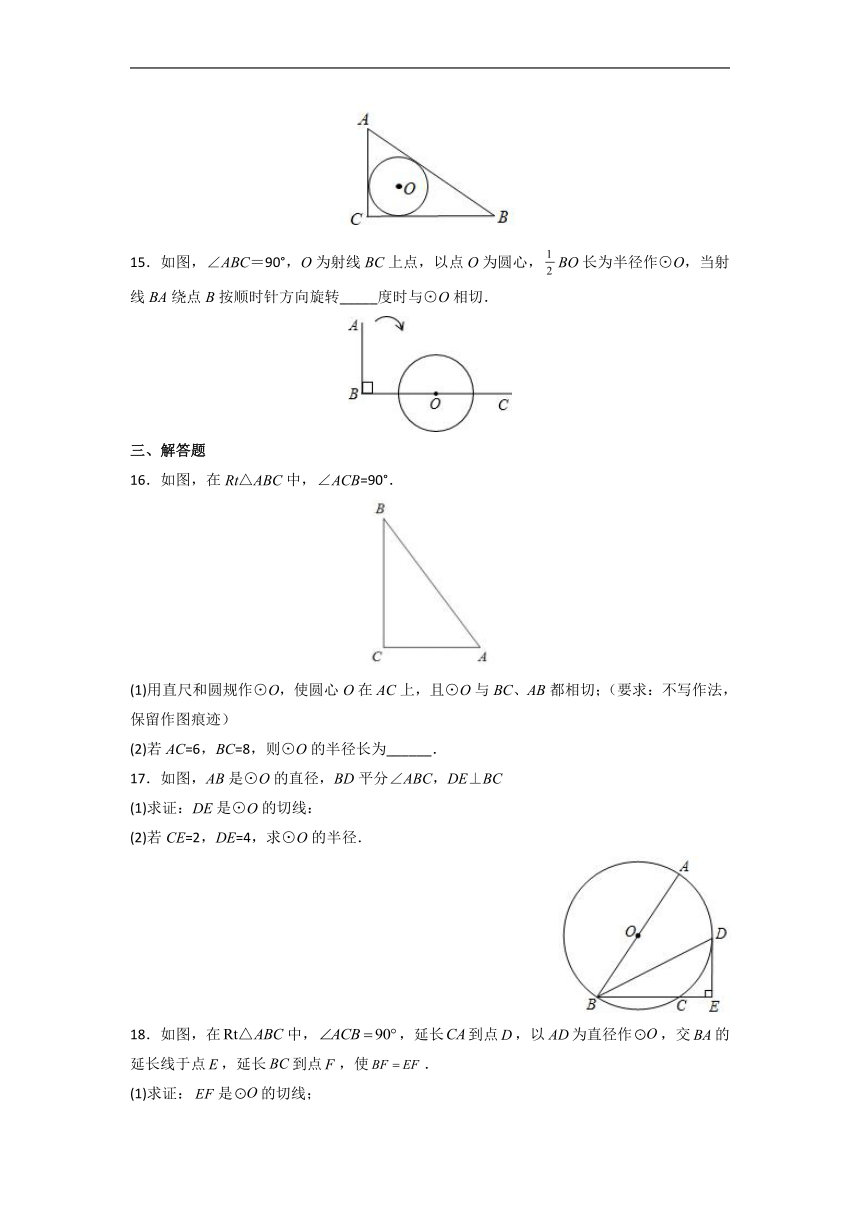
15.如图,∠ABC=90°,O为射线BC上点,以点O为圆心,BO长为半径作⊙O,当射线BA绕点B按顺时针方向旋转_____度时与⊙O相切.
三、解答题
16.如图,在Rt△ABC中,∠ACB=90°.
(1)用直尺和圆规作⊙O,使圆心O在AC上,且⊙O与BC、AB都相切;(要求:不写作法,保留作图痕迹)
(2)若AC=6,BC=8,则⊙O的半径长为______.
17.如图,AB是⊙O的直径,BD平分∠ABC,DE⊥BC
(1)求证:DE是⊙O的切线:
(2)若CE=2,DE=4,求⊙O的半径.
18.如图,在中,,延长到点,以为直径作,交的延长线于点,延长到点,使.
(1)求证:是的切线;
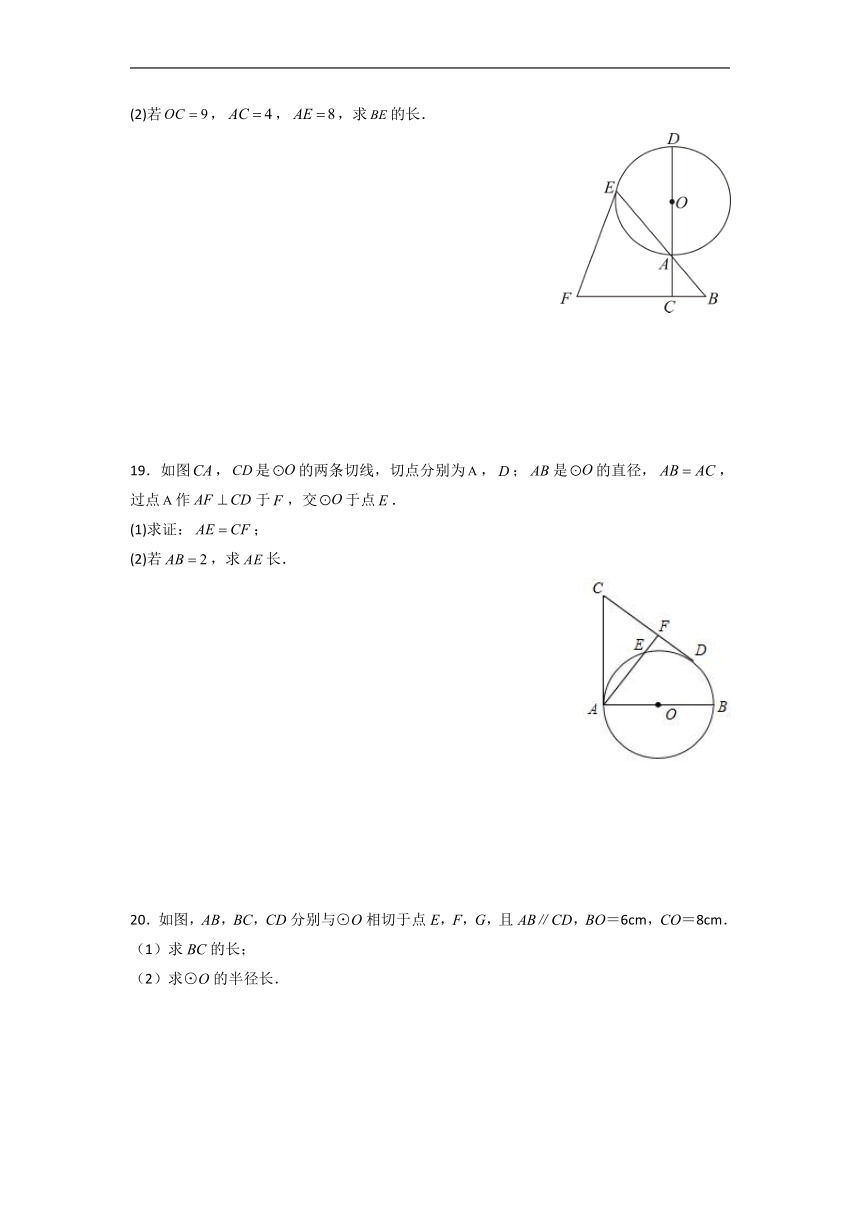
(2)若,,,求的长.
19.如图,是的两条切线,切点分别为,;是的直径,,过点作于,交于点.
(1)求证:;
(2)若,求长.
20.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6cm,CO=8cm.
(1)求BC的长;
(2)求⊙O的半径长.
21.已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
参考答案
一、单选题:1—10 CCCBA DCABD
二、填空题:
11.4或5 12.2 13.4 14.1 15.60或120
三、解答题:
16.(1)解:如图所示,⊙O即为所求.
.
(2).
17.(1)解:如图,连接OD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
又∵OB=OD,
∴∠ABD=∠ODB,
∴∠ODB=∠DBC,
∴OD∥BE,
∵DE⊥BE,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)如图,连接AC,交OD于F,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠FDE=90°,∠DEC=90°,
∴四边形FDEC是矩形,
∴DF=CE=2,FC=DE=4.
由垂径定理可知
设⊙O的半径为r,
在Rt△OAF中,由勾股定理得,
即(r-2)2+42=r2,
解得r=5.
即半径为5.
18.(1)如图,连接,
中,,
,
,
,
,
,
,
,
,
即,
是半径,
是的切线;
(2)如图,过点作,
,
,
,,
,
在与中,
,
,
19.(1)证明:连接,如图,
是的切线
,
,
是的直径,
,
,
,
,,
,
在和中,
,
,
;
(2)连接交于,如图,
是的切线,
,
,
,
,
,四边形为矩形,
,
,
设,则,
,是的两条切线,
,
而,
,
,
,
在中,,解得(舍去),,
的长为.
20.解:(1)∵AB,BC,CD分别与⊙O相切于E,F,G三点,
∴∠OBC=∠ABC,∠OCB=∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵OB=6cm,OC=8cm,
∴BC==10cm;
(2)如图,连接OF,
∵BC是⊙O的切线,
∴OF⊥BC,
∵S△BOC=OB OC=OF BC,
∴6×8=10×OF,解得:OF=cm,
即⊙O的半径为cm.
21.(1)连接OA、OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°﹣90°﹣90°﹣80°=100°,
由圆周角定理得,∠ACB= ∠AOB=50°;
(2)连接CE,
∵AE为⊙O的直径,
∴∠ACE=90°,
∵∠ACB=50°,
∴∠BCE=90°﹣50°=40°,
∴∠BAE=∠BCE=40°,
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB﹣∠ACB=20°.
一、单选题
1.已知⊙O的半径是4,OP=7,则点P与⊙O的位置关系是( ).
A.点P在圆内 B.点P在圆上 C.点P在圆外 D.不能确定
2.在平面直角坐标系中,以原点O为圆心,4为半径作圆,点P的坐标是(5,5),则点P与⊙O的位置关系是( )
A.点P在⊙O上 B.点P在⊙O内
C.点P在⊙O外 D.点P在⊙O上或在⊙O外
3.在数轴上,点所表示的实数为3,点所表示的实数为,的半径为2.下列说法中不正确的是( )
A.当时,点在上 B.当时,点在内
C.当时,点在内 D.当时,点在外
4.A,B两个点的坐标分别为(3,4),(﹣5,1),以原点O为圆心,5为半径作⊙O,则下列说法正确的是( )
A.点A,点B都在⊙O上 B.点A在⊙O上,点B在⊙O外
C.点A在⊙O内,点B在⊙O上 D.点A,点B都在⊙O外
5.如图,中,于点,点为上的点,,以点为圆心为半径画圆,下列说法错误的是( )
A.点在外 B.点在外
C.点在外 D.点在内
6.如图,△ABC中,∠ACB=90°,AC=BC,点D是边AC上一动点,连接BD,以CD为直径的圆交BD于点E.若AB长为4,则线段AE长的最小值为( )
A. B. C. D.
7.如图,点、、在上,,过点作的切线交的延长线于点,则的大小为( )
A. B. C. D.
8.如图,AB是⊙O的弦,PO⊥OA交AB于点P,过点B的切线交OP的延长线于点C,若⊙O的半径为,OP=1,则BC的长为( )
A.2 B. C. D.
9.如图,内切于,点P、点Q分别在直角边、斜边上,,且与相切,若,则的值为( )
A. B. C. D.
10.如图,点是的内心,的延长线和的外接圆相交于点,与相交于点,则下列结论:①;②若,则;③若点为的中点,则;④.其中一定正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题
11.已知在直角坐标平面内,以点P(﹣3,4)为圆心,r为半径画圆,⊙P与坐标轴恰好有三个交点,那么r的取值是 ______.
12.设P为外一点,若点P到的最短距离为2,最长距离为6,则的半径为______.
13.如图,PA、PB、MN分别与圆相切于点A、B、C,线段MN分别交PA、PB于点N、M,已知△PMN的周长是8,则PA的长度是_____.
14.如图,在中,,,,是内切圆,则的半径为______.
15.如图,∠ABC=90°,O为射线BC上点,以点O为圆心,BO长为半径作⊙O,当射线BA绕点B按顺时针方向旋转_____度时与⊙O相切.
三、解答题
16.如图,在Rt△ABC中,∠ACB=90°.
(1)用直尺和圆规作⊙O,使圆心O在AC上,且⊙O与BC、AB都相切;(要求:不写作法,保留作图痕迹)
(2)若AC=6,BC=8,则⊙O的半径长为______.
17.如图,AB是⊙O的直径,BD平分∠ABC,DE⊥BC
(1)求证:DE是⊙O的切线:
(2)若CE=2,DE=4,求⊙O的半径.
18.如图,在中,,延长到点,以为直径作,交的延长线于点,延长到点,使.
(1)求证:是的切线;
(2)若,,,求的长.
19.如图,是的两条切线,切点分别为,;是的直径,,过点作于,交于点.
(1)求证:;
(2)若,求长.
20.如图,AB,BC,CD分别与⊙O相切于点E,F,G,且AB∥CD,BO=6cm,CO=8cm.
(1)求BC的长;
(2)求⊙O的半径长.
21.已知PA,PB分别与⊙O相切于点A,B,∠APB=80°,C为⊙O上一点.
(1)如图①,求∠ACB的大小;
(2)如图②,AE为⊙O的直径,AE与BC相交于点D.若AB=AD,求∠EAC的大小.
参考答案
一、单选题:1—10 CCCBA DCABD
二、填空题:
11.4或5 12.2 13.4 14.1 15.60或120
三、解答题:
16.(1)解:如图所示,⊙O即为所求.
.
(2).
17.(1)解:如图,连接OD,
∵BD平分∠ABC,
∴∠ABD=∠DBC,
又∵OB=OD,
∴∠ABD=∠ODB,
∴∠ODB=∠DBC,
∴OD∥BE,
∵DE⊥BE,
∴OD⊥DE,
∴DE是⊙O的切线;
(2)如图,连接AC,交OD于F,
∵AB是⊙O的直径,
∴∠ACB=90°,
又∵∠FDE=90°,∠DEC=90°,
∴四边形FDEC是矩形,
∴DF=CE=2,FC=DE=4.
由垂径定理可知
设⊙O的半径为r,
在Rt△OAF中,由勾股定理得,
即(r-2)2+42=r2,
解得r=5.
即半径为5.
18.(1)如图,连接,
中,,
,
,
,
,
,
,
,
,
即,
是半径,
是的切线;
(2)如图,过点作,
,
,
,,
,
在与中,
,
,
19.(1)证明:连接,如图,
是的切线
,
,
是的直径,
,
,
,
,,
,
在和中,
,
,
;
(2)连接交于,如图,
是的切线,
,
,
,
,
,四边形为矩形,
,
,
设,则,
,是的两条切线,
,
而,
,
,
,
在中,,解得(舍去),,
的长为.
20.解:(1)∵AB,BC,CD分别与⊙O相切于E,F,G三点,
∴∠OBC=∠ABC,∠OCB=∠DCB,
∵AB∥CD,
∴∠ABC+∠DCB=180°,
∴∠OBC+∠OCB=90°,
∴∠BOC=90°,
∵OB=6cm,OC=8cm,
∴BC==10cm;
(2)如图,连接OF,
∵BC是⊙O的切线,
∴OF⊥BC,
∵S△BOC=OB OC=OF BC,
∴6×8=10×OF,解得:OF=cm,
即⊙O的半径为cm.
21.(1)连接OA、OB,
∵PA,PB是⊙O的切线,
∴∠OAP=∠OBP=90°,
∴∠AOB=360°﹣90°﹣90°﹣80°=100°,
由圆周角定理得,∠ACB= ∠AOB=50°;
(2)连接CE,
∵AE为⊙O的直径,
∴∠ACE=90°,
∵∠ACB=50°,
∴∠BCE=90°﹣50°=40°,
∴∠BAE=∠BCE=40°,
∵AB=AD,
∴∠ABD=∠ADB=70°,
∴∠EAC=∠ADB﹣∠ACB=20°.
同课章节目录
