2022—2023学年人教版数学七年级上册 第4章几何图形的初步 角的计算 分论讨论思想 练习(word版 含解析)
文档属性
| 名称 | 2022—2023学年人教版数学七年级上册 第4章几何图形的初步 角的计算 分论讨论思想 练习(word版 含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 766.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览



文档简介
角的计算 分类讨论
一.填空题(共13小题)
1.已知∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是 .
2.已知∠AOC=2∠BOC,∠BOC=30°,则∠AOB的度数为 .
3.已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OE平分∠AOC,则∠DOE的度数是 .
4.已知∠AOB=80°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 .
5.在同一平面内,O为直线AB上一点,射线OE将平角∠AOB分成∠AOE、∠BOE两部分,已知∠BOE=α,OC为∠AOE的平分线,∠DOE=90°,则∠COD= .(用含有α的代数式表示)
6.在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是 .
7.OC是∠AOB的平分线,从点O引出一条射线OD、使∠BOD∠COD,若∠BOD=15°,则∠AOB= °.
8.已知∠AOB=90°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 .
9.已知∠AOB=70°,∠AOD∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是 .
10.已知∠AOB=110°,∠AOD∠AOC,∠BOD=4∠BOC(∠BOC<35°),则∠COD的度数为 .
11.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 .
12.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线B的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 .
13.如图,∠COD在∠AOB的内部,且∠COD∠AOB,若将∠COD绕点O顺时针旋转,使∠COD在∠AOB的外部,在运动过程中,OE平分∠BOC,则∠DOE与∠AOC之间满足的数量关系是 .
二.解答题(共2小题)
14.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
15.【阅读理解】如图1,一套三角板如图拼在一起,我们将三角板COD绕点O以每秒15°的速度顺时针旋转180°.
【解决问题】
(1)在旋转过程中,∠AOB、∠AOC、∠BOC之间有怎样的数量关系?
(2)当运动时间为9秒时,图中有角平分线吗?找出并说明理由.
(3)运动过程中,如图2,形成的三个角:∠AOB、∠AOC、∠BOC,当其中一个角的度数是另一个角的两倍时,则称射线OC是∠AOB的“优线”.
①第(2)问中旋转后的射线OC是“优线”吗?为什么?
②在整个旋转过程中,若旋转时间记为t秒,当射线OC是“优线”时,请直接写出所有满足条件的t值.
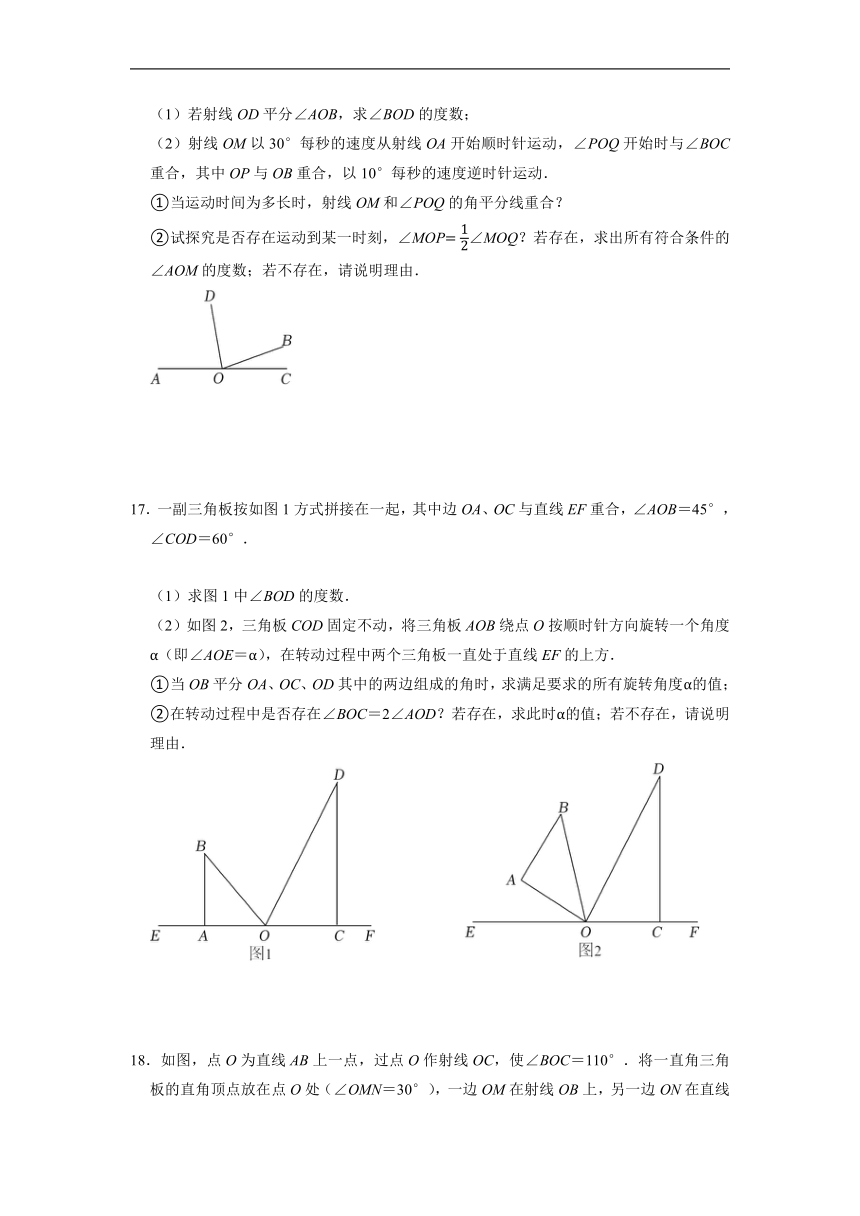
16.已知点A,O,C在同一条直线上,射线OB在AC上方,且∠BOC=20°,
(1)若射线OD平分∠AOB,求∠BOD的度数;
(2)射线OM以30°每秒的速度从射线OA开始顺时针运动,∠POQ开始时与∠BOC重合,其中OP与OB重合,以10°每秒的速度逆时针运动.
①当运动时间为多长时,射线OM和∠POQ的角平分线重合?
②试探究是否存在运动到某一时刻,∠MOP∠MOQ?若存在,求出所有符合条件的∠AOM的度数;若不存在,请说明理由.
17.一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数.
(2)如图2,三角板COD固定不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(即∠AOE=α),在转动过程中两个三角板一直处于直线EF的上方.
①当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度α的值;
②在转动过程中是否存在∠BOC=2∠AOD?若存在,求此时α的值;若不存在,请说明理由.
18.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.则∠BON= °.
(2)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
角的计算 分类讨论(解析)
一.填空题(共13小题)
1.已知∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是 45°或25° .
【解答】解:分为两种情况:如图①,当∠AOB在∠AOC的内部时,
∵∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,
∴∠AOD,
∴∠MOD=∠AOM﹣∠AOD=35°﹣10°=25°;
如图②,当∠AOB在∠AOC的外部时,
∵∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,
∴,
∴∠MOD=∠AOM+∠AOD=35°+10°=45°,
故答案为:25°或45°.
2.已知∠AOC=2∠BOC,∠BOC=30°,则∠AOB的度数为 90°或30° .
【解答】解:如图①,∠BOC在∠AOC的内部,
∵∠AOC=2∠BOC,∠BOC=30°,
∴∠AOC=60°,
∴∠AOB=∠AOC﹣∠BOC=60°﹣30°=30°;
如图②,①,∠BOC在∠AOC的外部,
∵∠AOC=2∠BOC,∠BOC=30°,
∴∠AOC=60°,
∴∠AOB=∠AOC+∠BOC=60°+30°=90°;
故答案为:30°或90°.
3.已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OE平分∠AOC,则∠DOE的度数是 30°或50° .
【解答】解:①如图,当OB在∠AOC的外部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°.
∵OD平分∠AOB,
∴∠AOD∠AOB=10°.
∵OE平分∠AOC,
∴∠AOE∠AOC=40°.
∴∠DOE=∠AOD+∠AOE=50°;
②如图,当OB在∠AOC的内部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°.
∵OD平分∠AOB,
∴∠AOD∠AOB=10°.
∵OE平分∠AOC,
∴∠AOE∠AOC=40°.
∴∠DOE=∠AOE﹣∠AOD=30°;
综上,∠DOE的度数是30°或50°.
故答案为:30°或50°.
4.已知∠AOB=80°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 5°或55° .
【解答】解:如图1,OD在∠AOB内,
∵∠AOB=80°,∠AOC=20°,
∴∠BOC=60°,
∵射线OE平分∠BOC,
∴∠EOC=30°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=∠EOC﹣∠COF=5°;
如图2,OD在∠AOB外,
∵∠AOB=80°,∠AOC=20°,
∴∠BOC=60°,
∵射线OE平分∠BOC,
∴∠EOC=30°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=∠EOC+∠COF=30°+25°=55°.
则∠EOF的度数是5°或55°.
故答案为:5°或55°.
5.在同一平面内,O为直线AB上一点,射线OE将平角∠AOB分成∠AOE、∠BOE两部分,已知∠BOE=α,OC为∠AOE的平分线,∠DOE=90°,则∠COD= 或180° .(用含有α的代数式表示)
【解答】解:①当射线OD,OE在直线AB的同侧时,如图所示:
∵OC为∠AOE的平分线,
∴∠1=∠2,
∵∠AOE+∠BOE=180°,∠BOE=α,
∴∠AOE=180°﹣α,
∴∠1=∠2(180°﹣α)=90°α,
∴∠COD=∠DOE+∠1=90°+90°180°;
②当射线OD、OE在直线AB的异侧时,如图所示:
∵OC为∠AOE的平分线,
∴∠l=∠2,
∵∠AOE+∠BOE=180°,∠BOE=α,
∴∠AOE=180°﹣α,
∴∠1=∠2(180°﹣α)=90°α,
∴∠COD=∠DOE﹣∠1=90°﹣(90°).
综上所述,∠COD或180°.
故答案为:或180°.
6.在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是 15°或65° .
【解答】解:①当OD在OC的左侧时,如图,
∵∠AOC=∠BOD=50°,∠AOB=20°,
∴∠AOD=∠BOD+∠AOB=70°,∠BOC=∠AOC﹣∠AOB=30°,
∴∠COD=∠BOD﹣∠BOC=20°,
∵OE平分∠AOD,
∴∠DOE∠AOD=35°,
∴∠COE=∠DOE﹣∠COD=15°;
②当OD在OA的下方时,如图,
∵∠AOC=∠BOD=50°,∠AOB=20°,
∴∠AOD=∠BOD﹣∠AOB=30°,
∵OE平分∠AOD,
∴∠AOE∠AOD=15°,
∴∠COE=∠AOC+∠AOE=65°.
综上所述,∠COE的度数为15°或65°.
故答案为:15°或65°.
7.OC是∠AOB的平分线,从点O引出一条射线OD、使∠BOD∠COD,若∠BOD=15°,则∠AOB= 120°或60 °.
【解答】解:①当射线OD在∠AOB的内部时,如图1,
∵∠BOD∠COD,∠BOD=15°,
∴∠COD=3∠BOD=45°,
∴∠BOC=∠BOD+∠COD=15°+45°=60°,
∵OC平分∠AOB,
∴∠AOB=2∠BOC=120°;
②当射线OD在∠AOB的外部时,如图2,
∵∠BOD∠COD,∠BOD=15°,
∴∠COD=3∠BOD=45°,
∴∠BOC=∠COD﹣∠BOD=45°+15°=30°,
∵OC平分∠AOB,
∴∠AOB=2∠BOC=60°;
综上,∠AOB=120°或60°.
故答案为:120°或60.
8.已知∠AOB=90°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 10°或60° .
【解答】解:如图1,OD在∠AOB内,
∵∠AOB=90°,∠AOC=20°,
∴∠BOC=70°,
∵射线OE平分∠BOC,
∴∠EOC=35°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=10°;
如图2,OD在∠AOB外,
∵∠AOB=90°,∠AOC=20°,
∴∠BOC=70°,
∵射线OE平分∠BOC,
∴∠EOC=35°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=60°.
则∠EOF的度数是10°或60°.
故答案为:10°或60°.
9.已知∠AOB=70°,∠AOD∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是 10°或14°或30°或42° .
【解答】解:设∠BOC=α,
∴∠BOD=3∠BOC=3α,
依据题意,分两种情况:
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:
i)若射线OD在∠AOC内部,如图1,
∴∠COD=∠BOD﹣∠BOC=2α,
∵∠AOD∠AOC,
∴∠AOD=∠COD=2α,
∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,
∴α=14°,
∴∠BOC=14°;
ii)若射线OD在∠AOB外部,如图2,
∴∠COD=∠BOD﹣∠BOC=2α,
∵∠AOD∠AOC,
∴∠AOD∠CODα,
∴∠AOB=∠BOD﹣∠AOD=3ααα=70°,
∴α=30°,
∴∠BOC=30°;
②当射线OC在∠AOB外部时,
依据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD∠AOC,
∴射线OD的位置也只有两种可能:
i)若射线DO在∠AOB内部,如图3,
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD∠AOC,
∴∠AOD=∠COD=4α,
∴∠AOB=∠BOD+∠AOD=4α,
∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°
ii)若射线OD在∠AOB外部,如图4,
则∠COD=∠BOC+∠DOB=4α,
∵∠AOD∠AOC,
∴∠AOD∠CODα,
∴∠AOB=∠BOD﹣∠AOD=3ααα=70°,
∴α=42°,
∴∠BOC=42°,
综上所述:∠BOC的度数分别是10°,14°,30°,42°.
故答案为:10°或14°或30°或42°
10.已知∠AOB=110°,∠AOD∠AOC,∠BOD=4∠BOC(∠BOC<35°),则∠COD的度数为 60°或或 .
【解答】解:(1)如图1所示:
当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,
设∠BOC=α,则∠BOD=4∠BOC=4α,
∴∠COD=∠BOD﹣∠BOC=3α,
∵∠AOD∠AOC,
∴3α+∠AOD=3∠AOD,
∴∠AODα,
∴∠AOB=∠AOD+∠BODα+4α=110°,
∴α=20°,
∴∠DOC=60°
②如图2所示,若射线OD在∠AOC外部,
设∠BOC=α,则∠BOD=4α,∠COD=∠BOD﹣∠BOC=3α,
∵∠AOD∠AOC,
∴∠AOD∠CODα,
∴∠AOB=∠BOD﹣∠AOD=4ααα=110°,
∴α.
∴∠DOC;
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
∵∠BOC<35°,∠AOD∠AOC,
∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,
∵∠COD=∠BOC+∠BOD=5α,
设∠AOD=β,则∠AOC=3β,
∴3β=5α+β,
∴βα,
∴∠AOB=∠BOD+∠AOD=4ααα=110°,
∴α,
∴∠DOC=5α;
②若射线OD在∠AOB外部,如图4所示,
设∠BOC=α,则∠BOD=4α,
∵∠AOB=110°,
∴∠AOD=∠BOD﹣∠AOB=4α﹣110°,
∠AOC=∠BOC+∠AOB=α+110°,
∵∠AOD∠AOC,
∴3(4α﹣110°)=α+110°
解得α=40°>35°,
此种情况不符合题意,
综上所述:∠COD的度数为:60°,,.
11.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 3或或 .
【解答】解:当∠NPQ∠MPN时,
15t(75+5t),
解得t=3;
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
故t的值为3或或.
故答案为:3或或.
12.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线B的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 5或23 .
【解答】解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON∠AOC=40°,
此时,三角板旋转的角度为90°﹣40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°﹣90°﹣40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故答案为:5或23.
13.如图,∠COD在∠AOB的内部,且∠COD∠AOB,若将∠COD绕点O顺时针旋转,使∠COD在∠AOB的外部,在运动过程中,OE平分∠BOC,则∠DOE与∠AOC之间满足的数量关系是 2∠DOE=∠AOC或∠AOC=360°﹣2∠DOE .
【解答】解:设∠COD=α,∠BOE=β,
如图1,当旋转角度小于180°时,
∵∠COD∠AOB,
∴∠AOB=2α,
∵OE平分∠BOC,
∴∠BOE=∠EOC=β,
∴∠DOE=∠EOC+∠COD=β+α,
∠AOC=∠AOB+∠BOC=2α+2β,
∴2∠DOE=∠AOC;
如图2,当旋转角度大于180°时,
∵∠COD∠AOB,
∴∠AOB=2α,
∵OE平分∠BOC,
∴∠BOE=∠EOC=β,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣3α﹣2β,
∴∠AOC=∠AOD+∠COD=360°﹣2α﹣2β,
∠DOE=∠DOC+∠COE=α+β,
∴∠AOC=360°﹣2∠DOE;
故答案为:2∠DOE=∠AOC或∠AOC=360°﹣2∠DOE.
二.解答题(共2小题)
14.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 是 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 20°或30°或40° 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
【解答】解:(1)一个角的平分线是这个角的“奇妙线”;
故答案为:是.
(2)①若∠MPN=60°,且射线PQ是∠MPN的“巧分线”,则由“巧分线”的定义可知有三种情况符合题意:
当∠NPQ=2∠MPQ时,∠QPN=40°,
当∠MPQ=2∠NPQ时,∠QPN=20°,
当∠NPM=2∠MPQ时,∠QPN=30°,
故答案为:20°或30°或40°;
②依题意有,3°45′=3.75°,
当3.75t=6060时,
解得t=24;
当3.75t=2×60时,
解得t=32;
当10t=60+2×60时,
解得t=48.
故当t为24或32或48时,射线PM是∠FPN的“奇妙线”;
15.【阅读理解】如图1,一套三角板如图拼在一起,我们将三角板COD绕点O以每秒15°的速度顺时针旋转180°.
【解决问题】
(1)在旋转过程中,∠AOB、∠AOC、∠BOC之间有怎样的数量关系?
(2)当运动时间为9秒时,图中有角平分线吗?找出并说明理由.
(3)运动过程中,如图2,形成的三个角:∠AOB、∠AOC、∠BOC,当其中一个角的度数是另一个角的两倍时,则称射线OC是∠AOB的“优线”.
①第(2)问中旋转后的射线OC是“优线”吗?为什么?
②在整个旋转过程中,若旋转时间记为t秒,当射线OC是“优线”时,请直接写出所有满足条件的t值.
【解答】解:(1)①如图,∠AOC+∠BOC=∠AOB,
②如图,∠AOC﹣∠BOC=∠AOB.
综上,∠AOC+∠BOC=∠AOB或∠AOC﹣∠BOC=∠AOB;
(2)有,射线OD平分∠AOB,射线OB平分∠COD.
如图,
理由:当运动时间为9秒时,∠AOC=15°×9=135°,
则∠BOC=∠AOC﹣∠AOB=135°﹣90°=45°,
因为∠COD=90°,
∴∠BOD=∠COD﹣∠BOC=90°﹣45°=45°,
∴∠BOC=∠BOD=45°,
∴射线OB平分∠COD.
又∠BOD=45°∠AOB,
∴射线OD平分∠AOB;
(3)①是.理由:
第(2)问中∠AOB=90°,∠AOC=135°,∠BOC=45°,
则∠AOB=2∠BOC,
所以OC是∠AOB的“优线”;
②由题意得,∠AOB=90°,∠AOC=15t,
当∠BOC=2∠AOC时,∠AOC=30°,
∴15t=30,解得t=2;
当∠AOB=2∠AOC时,∠AOC=45°,
∴15t=45,解得t=3;
当∠AOC=2∠BOC时,∠AOC=60°,
∴15t=60,解得t=4;
当∠AOB=2∠BOC时,∠AOC=135°,
∴15t=135,解得t=9;
当∠AOC=2∠AOB时,∠AOC=180°,
∴15t=180,解得t=12.
综上,t=2,3,4,9,12.
16.已知点A,O,C在同一条直线上,射线OB在AC上方,且∠BOC=20°,
(1)若射线OD平分∠AOB,求∠BOD的度数;
(2)射线OM以30°每秒的速度从射线OA开始顺时针运动,∠POQ开始时与∠BOC重合,其中OP与OB重合,以10°每秒的速度逆时针运动.
①当运动时间为多长时,射线OM和∠POQ的角平分线重合?
②试探究是否存在运动到某一时刻,∠MOP∠MOQ?若存在,求出所有符合条件的∠AOM的度数;若不存在,请说明理由.
【解答】解:(1)∵∠BOC=20°,点A、O、C在同一条直线上,
∴∠AOB=∠AOC﹣∠BOC=180°﹣20°=160°,
∵射线OD平分∠AOB,
∴∠BODAOB=80°;
(2)①如图,
由题意得,∠AOM=30t,∠POB=10t,∠POQ=20°,
∵射线OM和∠POQ的角平分线重合,
∴∠MOPPOQ=10°,
∴∠AOP=30t﹣10°,
∵∠AOP+∠POB+∠BOC=180°,
∴30t﹣10°+10t+20°=180°,
解得t,
答:当运动时间为秒时,射线OM和∠POQ的角平分线重合;
②当OM在∠POQ内部时,
∵∠MOP∠MOQ,
∴∠MOPPOQ,
∵∠MOP=∠AOM﹣∠AOP=30t﹣(160°﹣10t)﹣30t=40t﹣160°,
∴40t﹣160°20°,
解得t,
此时∠AOM=30t=125°;
当OM在∠POQ外部时,
∵∠MOP∠MOQ,
∴∠MOP=∠POQ,
∵∠MOP=∠AOP﹣∠AOM=(160°﹣10t)﹣30t=20°,
∴160°﹣40t=20°,
解得t,
此时,∠AOM=30t=105°;
综上,当t或时,∠MOP∠MOQ,此时∠AOM=125°或105°.
17.一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数.
(2)如图2,三角板COD固定不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(即∠AOE=α),在转动过程中两个三角板一直处于直线EF的上方.
①当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度α的值;
②在转动过程中是否存在∠BOC=2∠AOD?若存在,求此时α的值;若不存在,请说明理由.
【解答】解:(1)∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°﹣∠AOB﹣∠COD=75°;
(2)①当OB平分∠AOD时,
∵∠AOE=α,∠COD=60°,
∴∠AOD=180°﹣∠AOE﹣∠COD=120°﹣α,
∴∠AOB∠AOD=60°α=45°,
∴α=30°;
当OB平分∠AOC时,
∵∠AOC=180°﹣α,
∴∠AOB=90°α=45°,
∴α=90°;
当OB平分∠DOC时,
∵∠DOC=60°,
∴∠BOC=30°,
∴α=180°﹣45°﹣30°=105°,
综上所述,旋转角度α的值为30°,90°,105°;
②当OA在OD的左侧时,则∠AOD=120°﹣α,∠BOC=135°﹣α,
∵∠BOC=2∠AOD,
∴135°﹣α=2(120°﹣α),
∴α=105°;
当OA在OD的右侧时,则∠AOD=α﹣120°,∠BOC=135°﹣α,
∵∠BOC=2∠AOD,
∴135°﹣α=2(α﹣120),
∴α=125°,
综上所述,当α=105°或125°时,存在∠BOC=2∠AOD.
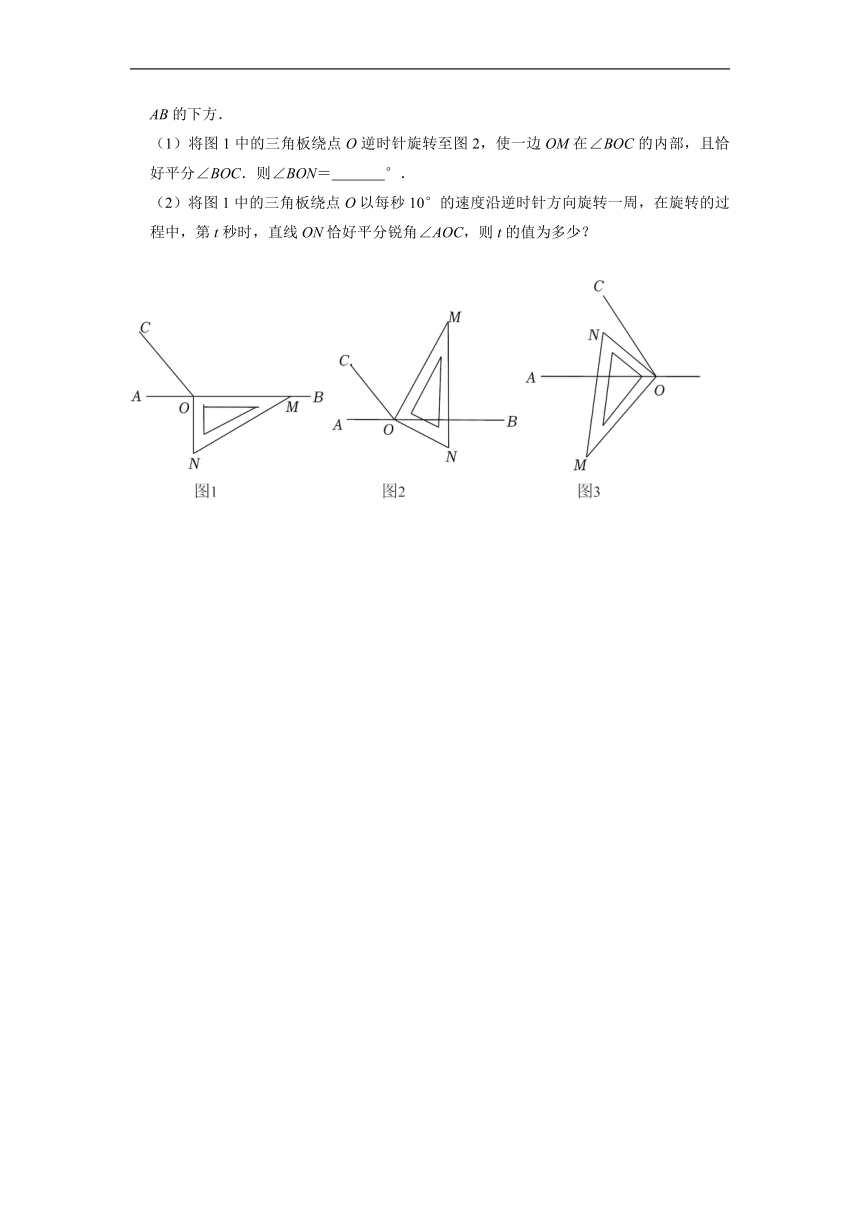
18.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.则∠BON= 35 °.
(2)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
【解答】解:(1)如图2,∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵∠BOC=110°
∴∠MOB=55°,
∵∠MON=90°,
∴∠BON=∠MON﹣∠MOB=35°;
故答案为:35;
(2)∵∠BOC=110°,
∴∠AOC=70°,
当直线NO恰好平分锐角∠AOC时,∠AOD=∠COD=35°,
∴∠BON=35°,∠BOM=55°,
即逆时针旋转的角度为55°,
由题意得,10t=55,t=5.5.
当ON平分∠AOC时,∠AON=35°,
∴∠AOM=55°,
即逆时针旋转的角度为:180°+55°=235°,
由题意得,10t=235,t=23.5.
综上所述,t=5.5或t=23.5.
一.填空题(共13小题)
1.已知∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是 .
2.已知∠AOC=2∠BOC,∠BOC=30°,则∠AOB的度数为 .
3.已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OE平分∠AOC,则∠DOE的度数是 .
4.已知∠AOB=80°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 .
5.在同一平面内,O为直线AB上一点,射线OE将平角∠AOB分成∠AOE、∠BOE两部分,已知∠BOE=α,OC为∠AOE的平分线,∠DOE=90°,则∠COD= .(用含有α的代数式表示)
6.在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是 .
7.OC是∠AOB的平分线,从点O引出一条射线OD、使∠BOD∠COD,若∠BOD=15°,则∠AOB= °.
8.已知∠AOB=90°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 .
9.已知∠AOB=70°,∠AOD∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是 .
10.已知∠AOB=110°,∠AOD∠AOC,∠BOD=4∠BOC(∠BOC<35°),则∠COD的度数为 .
11.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 .
12.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线B的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 .
13.如图,∠COD在∠AOB的内部,且∠COD∠AOB,若将∠COD绕点O顺时针旋转,使∠COD在∠AOB的外部,在运动过程中,OE平分∠BOC,则∠DOE与∠AOC之间满足的数量关系是 .
二.解答题(共2小题)
14.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
15.【阅读理解】如图1,一套三角板如图拼在一起,我们将三角板COD绕点O以每秒15°的速度顺时针旋转180°.
【解决问题】
(1)在旋转过程中,∠AOB、∠AOC、∠BOC之间有怎样的数量关系?
(2)当运动时间为9秒时,图中有角平分线吗?找出并说明理由.
(3)运动过程中,如图2,形成的三个角:∠AOB、∠AOC、∠BOC,当其中一个角的度数是另一个角的两倍时,则称射线OC是∠AOB的“优线”.
①第(2)问中旋转后的射线OC是“优线”吗?为什么?
②在整个旋转过程中,若旋转时间记为t秒,当射线OC是“优线”时,请直接写出所有满足条件的t值.
16.已知点A,O,C在同一条直线上,射线OB在AC上方,且∠BOC=20°,
(1)若射线OD平分∠AOB,求∠BOD的度数;
(2)射线OM以30°每秒的速度从射线OA开始顺时针运动,∠POQ开始时与∠BOC重合,其中OP与OB重合,以10°每秒的速度逆时针运动.
①当运动时间为多长时,射线OM和∠POQ的角平分线重合?
②试探究是否存在运动到某一时刻,∠MOP∠MOQ?若存在,求出所有符合条件的∠AOM的度数;若不存在,请说明理由.
17.一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数.
(2)如图2,三角板COD固定不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(即∠AOE=α),在转动过程中两个三角板一直处于直线EF的上方.
①当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度α的值;
②在转动过程中是否存在∠BOC=2∠AOD?若存在,求此时α的值;若不存在,请说明理由.
18.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.则∠BON= °.
(2)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
角的计算 分类讨论(解析)
一.填空题(共13小题)
1.已知∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,则∠MOD的度数是 45°或25° .
【解答】解:分为两种情况:如图①,当∠AOB在∠AOC的内部时,
∵∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,
∴∠AOD,
∴∠MOD=∠AOM﹣∠AOD=35°﹣10°=25°;
如图②,当∠AOB在∠AOC的外部时,
∵∠AOB=20°,∠AOC=70°,OD平分∠AOB,OM平分∠AOC,
∴,
∴∠MOD=∠AOM+∠AOD=35°+10°=45°,
故答案为:25°或45°.
2.已知∠AOC=2∠BOC,∠BOC=30°,则∠AOB的度数为 90°或30° .
【解答】解:如图①,∠BOC在∠AOC的内部,
∵∠AOC=2∠BOC,∠BOC=30°,
∴∠AOC=60°,
∴∠AOB=∠AOC﹣∠BOC=60°﹣30°=30°;
如图②,①,∠BOC在∠AOC的外部,
∵∠AOC=2∠BOC,∠BOC=30°,
∴∠AOC=60°,
∴∠AOB=∠AOC+∠BOC=60°+30°=90°;
故答案为:30°或90°.
3.已知∠AOB=20°,∠AOC=4∠AOB,OD平分∠AOB,OE平分∠AOC,则∠DOE的度数是 30°或50° .
【解答】解:①如图,当OB在∠AOC的外部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°.
∵OD平分∠AOB,
∴∠AOD∠AOB=10°.
∵OE平分∠AOC,
∴∠AOE∠AOC=40°.
∴∠DOE=∠AOD+∠AOE=50°;
②如图,当OB在∠AOC的内部时,
∵∠AOB=20°,∠AOC=4∠AOB,
∴∠AOC=80°.
∵OD平分∠AOB,
∴∠AOD∠AOB=10°.
∵OE平分∠AOC,
∴∠AOE∠AOC=40°.
∴∠DOE=∠AOE﹣∠AOD=30°;
综上,∠DOE的度数是30°或50°.
故答案为:30°或50°.
4.已知∠AOB=80°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 5°或55° .
【解答】解:如图1,OD在∠AOB内,
∵∠AOB=80°,∠AOC=20°,
∴∠BOC=60°,
∵射线OE平分∠BOC,
∴∠EOC=30°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=∠EOC﹣∠COF=5°;
如图2,OD在∠AOB外,
∵∠AOB=80°,∠AOC=20°,
∴∠BOC=60°,
∵射线OE平分∠BOC,
∴∠EOC=30°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=∠EOC+∠COF=30°+25°=55°.
则∠EOF的度数是5°或55°.
故答案为:5°或55°.
5.在同一平面内,O为直线AB上一点,射线OE将平角∠AOB分成∠AOE、∠BOE两部分,已知∠BOE=α,OC为∠AOE的平分线,∠DOE=90°,则∠COD= 或180° .(用含有α的代数式表示)
【解答】解:①当射线OD,OE在直线AB的同侧时,如图所示:
∵OC为∠AOE的平分线,
∴∠1=∠2,
∵∠AOE+∠BOE=180°,∠BOE=α,
∴∠AOE=180°﹣α,
∴∠1=∠2(180°﹣α)=90°α,
∴∠COD=∠DOE+∠1=90°+90°180°;
②当射线OD、OE在直线AB的异侧时,如图所示:
∵OC为∠AOE的平分线,
∴∠l=∠2,
∵∠AOE+∠BOE=180°,∠BOE=α,
∴∠AOE=180°﹣α,
∴∠1=∠2(180°﹣α)=90°α,
∴∠COD=∠DOE﹣∠1=90°﹣(90°).
综上所述,∠COD或180°.
故答案为:或180°.
6.在同一平面内,∠AOC=∠BOD=50°,射线OB在∠AOC的内部,且∠AOB=20°,OE平分∠AOD,则∠COE的度数是 15°或65° .
【解答】解:①当OD在OC的左侧时,如图,
∵∠AOC=∠BOD=50°,∠AOB=20°,
∴∠AOD=∠BOD+∠AOB=70°,∠BOC=∠AOC﹣∠AOB=30°,
∴∠COD=∠BOD﹣∠BOC=20°,
∵OE平分∠AOD,
∴∠DOE∠AOD=35°,
∴∠COE=∠DOE﹣∠COD=15°;
②当OD在OA的下方时,如图,
∵∠AOC=∠BOD=50°,∠AOB=20°,
∴∠AOD=∠BOD﹣∠AOB=30°,
∵OE平分∠AOD,
∴∠AOE∠AOD=15°,
∴∠COE=∠AOC+∠AOE=65°.
综上所述,∠COE的度数为15°或65°.
故答案为:15°或65°.
7.OC是∠AOB的平分线,从点O引出一条射线OD、使∠BOD∠COD,若∠BOD=15°,则∠AOB= 120°或60 °.
【解答】解:①当射线OD在∠AOB的内部时,如图1,
∵∠BOD∠COD,∠BOD=15°,
∴∠COD=3∠BOD=45°,
∴∠BOC=∠BOD+∠COD=15°+45°=60°,
∵OC平分∠AOB,
∴∠AOB=2∠BOC=120°;
②当射线OD在∠AOB的外部时,如图2,
∵∠BOD∠COD,∠BOD=15°,
∴∠COD=3∠BOD=45°,
∴∠BOC=∠COD﹣∠BOD=45°+15°=30°,
∵OC平分∠AOB,
∴∠AOB=2∠BOC=60°;
综上,∠AOB=120°或60°.
故答案为:120°或60.
8.已知∠AOB=90°,射线OC在∠AOB内部,且∠AOC=20°,∠COD=50°,射线OE、OF分别平分∠BOC、∠COD,则∠EOF的度数是 10°或60° .
【解答】解:如图1,OD在∠AOB内,
∵∠AOB=90°,∠AOC=20°,
∴∠BOC=70°,
∵射线OE平分∠BOC,
∴∠EOC=35°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=10°;
如图2,OD在∠AOB外,
∵∠AOB=90°,∠AOC=20°,
∴∠BOC=70°,
∵射线OE平分∠BOC,
∴∠EOC=35°,
∵射线OF平分∠COD,∠COD=50°,
∴∠FOC=25°,
∴∠EOF=60°.
则∠EOF的度数是10°或60°.
故答案为:10°或60°.
9.已知∠AOB=70°,∠AOD∠AOC,∠BOD=3∠BOC(∠BOC<45°),则∠BOC的度数是 10°或14°或30°或42° .
【解答】解:设∠BOC=α,
∴∠BOD=3∠BOC=3α,
依据题意,分两种情况:
①当射线OC在∠AOB内部时,此时射线OD的位置只有两种可能:
i)若射线OD在∠AOC内部,如图1,
∴∠COD=∠BOD﹣∠BOC=2α,
∵∠AOD∠AOC,
∴∠AOD=∠COD=2α,
∴∠AOB=∠AOD+∠BOD=2α+3α=5α=70°,
∴α=14°,
∴∠BOC=14°;
ii)若射线OD在∠AOB外部,如图2,
∴∠COD=∠BOD﹣∠BOC=2α,
∵∠AOD∠AOC,
∴∠AOD∠CODα,
∴∠AOB=∠BOD﹣∠AOD=3ααα=70°,
∴α=30°,
∴∠BOC=30°;
②当射线OC在∠AOB外部时,
依据题意,此时射线OC靠近射线OB,
∵∠BOC<45°,∠AOD∠AOC,
∴射线OD的位置也只有两种可能:
i)若射线DO在∠AOB内部,如图3,
则∠COD=∠BOC+∠BOD=4α,
∵∠AOD∠AOC,
∴∠AOD=∠COD=4α,
∴∠AOB=∠BOD+∠AOD=4α,
∴∠AOB=∠BOD+∠AOD=3α+4α=7α=70°,
∴α=10°,
∴∠BOC=10°
ii)若射线OD在∠AOB外部,如图4,
则∠COD=∠BOC+∠DOB=4α,
∵∠AOD∠AOC,
∴∠AOD∠CODα,
∴∠AOB=∠BOD﹣∠AOD=3ααα=70°,
∴α=42°,
∴∠BOC=42°,
综上所述:∠BOC的度数分别是10°,14°,30°,42°.
故答案为:10°或14°或30°或42°
10.已知∠AOB=110°,∠AOD∠AOC,∠BOD=4∠BOC(∠BOC<35°),则∠COD的度数为 60°或或 .
【解答】解:(1)如图1所示:
当射线OC在∠AOB的内部时,①若射线OD在∠AOC内部,
设∠BOC=α,则∠BOD=4∠BOC=4α,
∴∠COD=∠BOD﹣∠BOC=3α,
∵∠AOD∠AOC,
∴3α+∠AOD=3∠AOD,
∴∠AODα,
∴∠AOB=∠AOD+∠BODα+4α=110°,
∴α=20°,
∴∠DOC=60°
②如图2所示,若射线OD在∠AOC外部,
设∠BOC=α,则∠BOD=4α,∠COD=∠BOD﹣∠BOC=3α,
∵∠AOD∠AOC,
∴∠AOD∠CODα,
∴∠AOB=∠BOD﹣∠AOD=4ααα=110°,
∴α.
∴∠DOC;
(2)当射线OC在∠AOB外部时,根据题意,此时射线OC靠近射线OB,
∵∠BOC<35°,∠AOD∠AOC,
∴射线OD的位置也只有两种可能;
①若射线OD在∠AOB内部,如图3所示,
∵∠COD=∠BOC+∠BOD=5α,
设∠AOD=β,则∠AOC=3β,
∴3β=5α+β,
∴βα,
∴∠AOB=∠BOD+∠AOD=4ααα=110°,
∴α,
∴∠DOC=5α;
②若射线OD在∠AOB外部,如图4所示,
设∠BOC=α,则∠BOD=4α,
∵∠AOB=110°,
∴∠AOD=∠BOD﹣∠AOB=4α﹣110°,
∠AOC=∠BOC+∠AOB=α+110°,
∵∠AOD∠AOC,
∴3(4α﹣110°)=α+110°
解得α=40°>35°,
此种情况不符合题意,
综上所述:∠COD的度数为:60°,,.
11.如图1,射线OC在∠AOB的内部,图中共有3个角:∠AOB,∠AOC和∠BOC,若其中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的“巧分线”.如图2,若∠MPN=75°,且射线PQ绕点P从PN位置开始,以每秒15°的速度逆时针旋转,射线PM同时绕点P以每秒5°的速度逆时针旋转,当PQ与PN成180°时,PQ与PM同时停止旋转,设旋转的时间为t秒.当射线PQ是∠MPN的“巧分线”时,t的值为 3或或 .
【解答】解:当∠NPQ∠MPN时,
15t(75+5t),
解得t=3;
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
当∠NPQ∠MPN时,
15t(75+5t),
解得t.
故t的值为3或或.
故答案为:3或或.
12.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线B的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 5或23 .
【解答】解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON∠AOC=40°,
此时,三角板旋转的角度为90°﹣40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°﹣90°﹣40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故答案为:5或23.
13.如图,∠COD在∠AOB的内部,且∠COD∠AOB,若将∠COD绕点O顺时针旋转,使∠COD在∠AOB的外部,在运动过程中,OE平分∠BOC,则∠DOE与∠AOC之间满足的数量关系是 2∠DOE=∠AOC或∠AOC=360°﹣2∠DOE .
【解答】解:设∠COD=α,∠BOE=β,
如图1,当旋转角度小于180°时,
∵∠COD∠AOB,
∴∠AOB=2α,
∵OE平分∠BOC,
∴∠BOE=∠EOC=β,
∴∠DOE=∠EOC+∠COD=β+α,
∠AOC=∠AOB+∠BOC=2α+2β,
∴2∠DOE=∠AOC;
如图2,当旋转角度大于180°时,
∵∠COD∠AOB,
∴∠AOB=2α,
∵OE平分∠BOC,
∴∠BOE=∠EOC=β,
∴∠AOD=360°﹣∠AOB﹣∠BOC﹣∠COD=360°﹣3α﹣2β,
∴∠AOC=∠AOD+∠COD=360°﹣2α﹣2β,
∠DOE=∠DOC+∠COE=α+β,
∴∠AOC=360°﹣2∠DOE;
故答案为:2∠DOE=∠AOC或∠AOC=360°﹣2∠DOE.
二.解答题(共2小题)
14.已知射线OC在∠AOB的内部,若∠AOB,∠AOC和∠BOC三个角中有一个角的度数是另一个角度数的两倍,则称射线OC是∠AOB的奇妙线.
(1)一个角的平分线 是 这个角的奇妙线;(填“是”或“不是”)
(2)如图,∠MPN=60°.
①若射线PQ是∠MPN的奇妙线,则∠QPN的度数为 20°或30°或40° 度;
②射线PF从PN位置开始,以每秒旋转3°45'的速度绕点P按逆时针方向旋转,当
∠FPN首次等于180°时停止旋转,设旋转的时间为t(s).当t为何值时,射线PM是∠FPN的奇妙线?
【解答】解:(1)一个角的平分线是这个角的“奇妙线”;
故答案为:是.
(2)①若∠MPN=60°,且射线PQ是∠MPN的“巧分线”,则由“巧分线”的定义可知有三种情况符合题意:
当∠NPQ=2∠MPQ时,∠QPN=40°,
当∠MPQ=2∠NPQ时,∠QPN=20°,
当∠NPM=2∠MPQ时,∠QPN=30°,
故答案为:20°或30°或40°;
②依题意有,3°45′=3.75°,
当3.75t=6060时,
解得t=24;
当3.75t=2×60时,
解得t=32;
当10t=60+2×60时,
解得t=48.
故当t为24或32或48时,射线PM是∠FPN的“奇妙线”;
15.【阅读理解】如图1,一套三角板如图拼在一起,我们将三角板COD绕点O以每秒15°的速度顺时针旋转180°.
【解决问题】
(1)在旋转过程中,∠AOB、∠AOC、∠BOC之间有怎样的数量关系?
(2)当运动时间为9秒时,图中有角平分线吗?找出并说明理由.
(3)运动过程中,如图2,形成的三个角:∠AOB、∠AOC、∠BOC,当其中一个角的度数是另一个角的两倍时,则称射线OC是∠AOB的“优线”.
①第(2)问中旋转后的射线OC是“优线”吗?为什么?
②在整个旋转过程中,若旋转时间记为t秒,当射线OC是“优线”时,请直接写出所有满足条件的t值.
【解答】解:(1)①如图,∠AOC+∠BOC=∠AOB,
②如图,∠AOC﹣∠BOC=∠AOB.
综上,∠AOC+∠BOC=∠AOB或∠AOC﹣∠BOC=∠AOB;
(2)有,射线OD平分∠AOB,射线OB平分∠COD.
如图,
理由:当运动时间为9秒时,∠AOC=15°×9=135°,
则∠BOC=∠AOC﹣∠AOB=135°﹣90°=45°,
因为∠COD=90°,
∴∠BOD=∠COD﹣∠BOC=90°﹣45°=45°,
∴∠BOC=∠BOD=45°,
∴射线OB平分∠COD.
又∠BOD=45°∠AOB,
∴射线OD平分∠AOB;
(3)①是.理由:
第(2)问中∠AOB=90°,∠AOC=135°,∠BOC=45°,
则∠AOB=2∠BOC,
所以OC是∠AOB的“优线”;
②由题意得,∠AOB=90°,∠AOC=15t,
当∠BOC=2∠AOC时,∠AOC=30°,
∴15t=30,解得t=2;
当∠AOB=2∠AOC时,∠AOC=45°,
∴15t=45,解得t=3;
当∠AOC=2∠BOC时,∠AOC=60°,
∴15t=60,解得t=4;
当∠AOB=2∠BOC时,∠AOC=135°,
∴15t=135,解得t=9;
当∠AOC=2∠AOB时,∠AOC=180°,
∴15t=180,解得t=12.
综上,t=2,3,4,9,12.
16.已知点A,O,C在同一条直线上,射线OB在AC上方,且∠BOC=20°,
(1)若射线OD平分∠AOB,求∠BOD的度数;
(2)射线OM以30°每秒的速度从射线OA开始顺时针运动,∠POQ开始时与∠BOC重合,其中OP与OB重合,以10°每秒的速度逆时针运动.
①当运动时间为多长时,射线OM和∠POQ的角平分线重合?
②试探究是否存在运动到某一时刻,∠MOP∠MOQ?若存在,求出所有符合条件的∠AOM的度数;若不存在,请说明理由.
【解答】解:(1)∵∠BOC=20°,点A、O、C在同一条直线上,
∴∠AOB=∠AOC﹣∠BOC=180°﹣20°=160°,
∵射线OD平分∠AOB,
∴∠BODAOB=80°;
(2)①如图,
由题意得,∠AOM=30t,∠POB=10t,∠POQ=20°,
∵射线OM和∠POQ的角平分线重合,
∴∠MOPPOQ=10°,
∴∠AOP=30t﹣10°,
∵∠AOP+∠POB+∠BOC=180°,
∴30t﹣10°+10t+20°=180°,
解得t,
答:当运动时间为秒时,射线OM和∠POQ的角平分线重合;
②当OM在∠POQ内部时,
∵∠MOP∠MOQ,
∴∠MOPPOQ,
∵∠MOP=∠AOM﹣∠AOP=30t﹣(160°﹣10t)﹣30t=40t﹣160°,
∴40t﹣160°20°,
解得t,
此时∠AOM=30t=125°;
当OM在∠POQ外部时,
∵∠MOP∠MOQ,
∴∠MOP=∠POQ,
∵∠MOP=∠AOP﹣∠AOM=(160°﹣10t)﹣30t=20°,
∴160°﹣40t=20°,
解得t,
此时,∠AOM=30t=105°;
综上,当t或时,∠MOP∠MOQ,此时∠AOM=125°或105°.
17.一副三角板按如图1方式拼接在一起,其中边OA、OC与直线EF重合,∠AOB=45°,∠COD=60°.
(1)求图1中∠BOD的度数.
(2)如图2,三角板COD固定不动,将三角板AOB绕点O按顺时针方向旋转一个角度α(即∠AOE=α),在转动过程中两个三角板一直处于直线EF的上方.
①当OB平分OA、OC、OD其中的两边组成的角时,求满足要求的所有旋转角度α的值;
②在转动过程中是否存在∠BOC=2∠AOD?若存在,求此时α的值;若不存在,请说明理由.
【解答】解:(1)∵∠AOB=45°,∠COD=60°,
∴∠BOD=180°﹣∠AOB﹣∠COD=75°;
(2)①当OB平分∠AOD时,
∵∠AOE=α,∠COD=60°,
∴∠AOD=180°﹣∠AOE﹣∠COD=120°﹣α,
∴∠AOB∠AOD=60°α=45°,
∴α=30°;
当OB平分∠AOC时,
∵∠AOC=180°﹣α,
∴∠AOB=90°α=45°,
∴α=90°;
当OB平分∠DOC时,
∵∠DOC=60°,
∴∠BOC=30°,
∴α=180°﹣45°﹣30°=105°,
综上所述,旋转角度α的值为30°,90°,105°;
②当OA在OD的左侧时,则∠AOD=120°﹣α,∠BOC=135°﹣α,
∵∠BOC=2∠AOD,
∴135°﹣α=2(120°﹣α),
∴α=105°;
当OA在OD的右侧时,则∠AOD=α﹣120°,∠BOC=135°﹣α,
∵∠BOC=2∠AOD,
∴135°﹣α=2(α﹣120),
∴α=125°,
综上所述,当α=105°或125°时,存在∠BOC=2∠AOD.
18.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.则∠BON= 35 °.
(2)将图1中的三角板绕点O以每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
【解答】解:(1)如图2,∵OM平分∠BOC,
∴∠MOC=∠MOB,
又∵∠BOC=110°
∴∠MOB=55°,
∵∠MON=90°,
∴∠BON=∠MON﹣∠MOB=35°;
故答案为:35;
(2)∵∠BOC=110°,
∴∠AOC=70°,
当直线NO恰好平分锐角∠AOC时,∠AOD=∠COD=35°,
∴∠BON=35°,∠BOM=55°,
即逆时针旋转的角度为55°,
由题意得,10t=55,t=5.5.
当ON平分∠AOC时,∠AON=35°,
∴∠AOM=55°,
即逆时针旋转的角度为:180°+55°=235°,
由题意得,10t=235,t=23.5.
综上所述,t=5.5或t=23.5.
