沪科版八年级上册15.4角的平分线(第1课时) 课件(共18张PPT)
文档属性
| 名称 | 沪科版八年级上册15.4角的平分线(第1课时) 课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 07:06:05 | ||
图片预览





文档简介
(共18张PPT)
第 15章 轴对称图形与等腰三角形
15.4 角的平分线
第1课时 角平分线的作法
学习目标
1.能够利用尺规法作一个角的平分线,并能证明它的正确性;(重点)
2.能够运用尺规过一点作已知直线的垂线.(难点)
知识回顾
1.角平分线的定义:
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
O
B
A
C
1.作一条线段等于已知线段;
2.作一个角等于已知角;
3.作已知线段的垂直平分线.
2.我们学过的基本作图?
想一想:
新课导入
请你将一张用纸片做的角分成两个相等的角.你有什么办法?
A
O
B
C
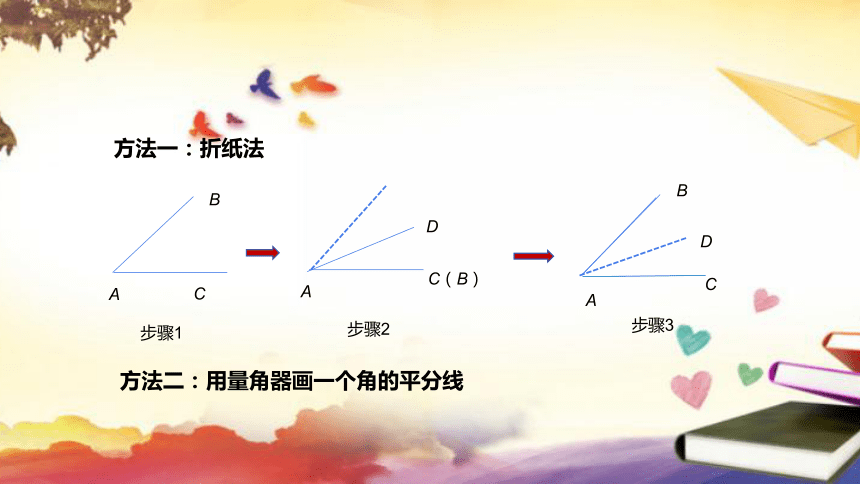
方法一:折纸法
方法二:用量角器画一个角的平分线
C
A
步骤1
C
A
步骤3
C(B)
D
B
D
步骤2
B
A
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
观察下面简易的平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB 和AD 沿着角的两边放下,沿AC画一条射线AE,AE 就是∠DAB 的平分线.你能说明它的道理吗?
想一想:
证明:
在△ACD 和△ACB 中,
AD=AB,(已知)
DC=BC,(已知)
CA=CA,(公共边)
∴ △ACD≌△ACB,(SSS)
∴∠CAD=∠CAB,(全等三角形的对应角相等)
∴AC平分∠DAB.(角平分线的定义)
根据角平分仪的制作原理怎样作一个角的平分线? (不用角平分仪或量角器)
知识讲解
已知:∠AOB,如图.
求作:射线OP,使∠AOP =∠BOP.
作法:
1.用尺规作角的平分线
(1)以点O为圆心,任意长为半径画弧,交OA 、OB于点M、点N.
(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在 ∠AOB内部相交于点P..
(3)画射线OP.射线OP 即为所求.
A
B
O
N
M
P
问题:
请你说明OP为什么是∠MON的平分线,并与同伴进行交流.
证明:连接PM,PN,
在△MOP 和△NOP 中,
OM=ON,(已知)
OP=OP,(已知)
MP=NP,(公共边)
∴ △MOP≌△NOP,(SSS)
∴∠MCP=∠NCP,(全等三角形的对应角相等)
∴OP平分∠MON.(角平分线的定义)
N
M
P
O
思考?
当∠AOB 的两边成一条直线时,你会作这个角的平分线吗?这时的角平分线与AB是什么位置关系?
N
M
P
O
A
B
答案:OP ⊥AB
思考?
如何经过一点作已知直线的垂线?
E
D
F
C
A
B
已知:直线AB和AB上的一点C.
求作:AB的垂线,使它经过点C.
1.经过已知直线上一点作这条直线的垂线
作法:
1.以点C为圆心,任意长为半径画弧,交直线与D,E 两点;
2. 分别以点D,E 为圆心,大于 DE的长为半径画弧,两弧相交于点F;
3.作直线CF.
直线CF就是所求作的垂线.
2.过一点作已知直线的垂线
已知:直线AB和AB外的一点C.
求作:AB的垂线,使它经过点C.
作法:
1.任取一点K,使K和C在AB的两旁;
2.以点C为圆心,CK长为半径作弧,交AB与点D和E ;
3. 分别以点D和E 为圆心,大于 DE的长为半径作弧,两弧交于点F;
3.作直线CF.
直线CF就是所求作的垂线.
E
D
F
C
A
B
K
思考
为什么作出的直线CF就是所求作的垂线?你能说明道理吗?
证明:连接CD,CE,FD,FE
E
D
F
C
A
B
K
由作法知,FD=FE,
∴点F在线段DE 的垂直平分线上,
由作法知,CD=CE,
∴点C在线段DE 的垂直平分线上,
∴CF是线段DE的垂直平分线,
即直线CF垂直直线AB.
随堂训练
1.
用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角平分线上的点到角两边的距离相等
A
A
B
O
N
M
C
已知:线段a,b,如图.
求作:△ABC,使底边BC=a,BC边上的高AD=h.
作法:
2.已知等腰三角形底边是a,底边上的高是b,求作:等腰三角形.
(1)作线段BC=a;
(2)分别以点B,C为圆心,大于 BC的长为半径画弧,两弧相交于点M,N;
(4)以点D为圆心,以b为半径画弧,交直线MN与点A;
a
b
(3)作直线MN.交线段AB与点D;
(5)连接AB,AC,则△ABC为所求作的三角形.
B
C
M
N
D
A
课堂小结
1.用尺规作图作一个已知角的平分线;
2.过一点作已知直线的垂线
经过已知直线上一点作已知直线的垂线
经过已知直线外一点作已知直线的垂线
第 15章 轴对称图形与等腰三角形
15.4 角的平分线
第1课时 角平分线的作法
学习目标
1.能够利用尺规法作一个角的平分线,并能证明它的正确性;(重点)
2.能够运用尺规过一点作已知直线的垂线.(难点)
知识回顾
1.角平分线的定义:
从一个角的顶点出发,把这个角分成两个相等的角的射线,叫做这个角的平分线.
O
B
A
C
1.作一条线段等于已知线段;
2.作一个角等于已知角;
3.作已知线段的垂直平分线.
2.我们学过的基本作图?
想一想:
新课导入
请你将一张用纸片做的角分成两个相等的角.你有什么办法?
A
O
B
C
方法一:折纸法
方法二:用量角器画一个角的平分线
C
A
步骤1
C
A
步骤3
C(B)
D
B
D
步骤2
B
A
如果前面活动中的纸片换成木板、钢板等没法折的角,又该怎么办呢?
观察下面简易的平分角的仪器,其中AB=AD,BC=DC.将点A放在角的顶点,AB 和AD 沿着角的两边放下,沿AC画一条射线AE,AE 就是∠DAB 的平分线.你能说明它的道理吗?
想一想:
证明:
在△ACD 和△ACB 中,
AD=AB,(已知)
DC=BC,(已知)
CA=CA,(公共边)
∴ △ACD≌△ACB,(SSS)
∴∠CAD=∠CAB,(全等三角形的对应角相等)
∴AC平分∠DAB.(角平分线的定义)
根据角平分仪的制作原理怎样作一个角的平分线? (不用角平分仪或量角器)
知识讲解
已知:∠AOB,如图.
求作:射线OP,使∠AOP =∠BOP.
作法:
1.用尺规作角的平分线
(1)以点O为圆心,任意长为半径画弧,交OA 、OB于点M、点N.
(2)分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在 ∠AOB内部相交于点P..
(3)画射线OP.射线OP 即为所求.
A
B
O
N
M
P
问题:
请你说明OP为什么是∠MON的平分线,并与同伴进行交流.
证明:连接PM,PN,
在△MOP 和△NOP 中,
OM=ON,(已知)
OP=OP,(已知)
MP=NP,(公共边)
∴ △MOP≌△NOP,(SSS)
∴∠MCP=∠NCP,(全等三角形的对应角相等)
∴OP平分∠MON.(角平分线的定义)
N
M
P
O
思考?
当∠AOB 的两边成一条直线时,你会作这个角的平分线吗?这时的角平分线与AB是什么位置关系?
N
M
P
O
A
B
答案:OP ⊥AB
思考?
如何经过一点作已知直线的垂线?
E
D
F
C
A
B
已知:直线AB和AB上的一点C.
求作:AB的垂线,使它经过点C.
1.经过已知直线上一点作这条直线的垂线
作法:
1.以点C为圆心,任意长为半径画弧,交直线与D,E 两点;
2. 分别以点D,E 为圆心,大于 DE的长为半径画弧,两弧相交于点F;
3.作直线CF.
直线CF就是所求作的垂线.
2.过一点作已知直线的垂线
已知:直线AB和AB外的一点C.
求作:AB的垂线,使它经过点C.
作法:
1.任取一点K,使K和C在AB的两旁;
2.以点C为圆心,CK长为半径作弧,交AB与点D和E ;
3. 分别以点D和E 为圆心,大于 DE的长为半径作弧,两弧交于点F;
3.作直线CF.
直线CF就是所求作的垂线.
E
D
F
C
A
B
K
思考
为什么作出的直线CF就是所求作的垂线?你能说明道理吗?
证明:连接CD,CE,FD,FE
E
D
F
C
A
B
K
由作法知,FD=FE,
∴点F在线段DE 的垂直平分线上,
由作法知,CD=CE,
∴点C在线段DE 的垂直平分线上,
∴CF是线段DE的垂直平分线,
即直线CF垂直直线AB.
随堂训练
1.
用尺规作图作一个已知角的平分线的示意图如图所示,则能说明∠AOC=∠BOC的依据是( )
A.SSS B.ASA
C.AAS D.角平分线上的点到角两边的距离相等
A
A
B
O
N
M
C
已知:线段a,b,如图.
求作:△ABC,使底边BC=a,BC边上的高AD=h.
作法:
2.已知等腰三角形底边是a,底边上的高是b,求作:等腰三角形.
(1)作线段BC=a;
(2)分别以点B,C为圆心,大于 BC的长为半径画弧,两弧相交于点M,N;
(4)以点D为圆心,以b为半径画弧,交直线MN与点A;
a
b
(3)作直线MN.交线段AB与点D;
(5)连接AB,AC,则△ABC为所求作的三角形.
B
C
M
N
D
A
课堂小结
1.用尺规作图作一个已知角的平分线;
2.过一点作已知直线的垂线
经过已知直线上一点作已知直线的垂线
经过已知直线外一点作已知直线的垂线
