沪科版八年级上册15.3等腰三角形(第1课时) 课件(共28张PPT)
文档属性
| 名称 | 沪科版八年级上册15.3等腰三角形(第1课时) 课件(共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-08-08 00:00:00 | ||
图片预览




文档简介
(共28张PPT)
15.3 等腰三角形
第1课时 等腰三角形的性质
第15章 轴对称图形与等腰三角形
理解并掌握等腰三角形的性质及其推论;(重点)
能运用等腰三角形的性质及其推论解决基本的几何问题.(难点)
学习目标
1
2
3
经历操作、思考、探究证明等腰三角形的有关定理的过程,进一步掌握证明的基本步骤和书写格式;
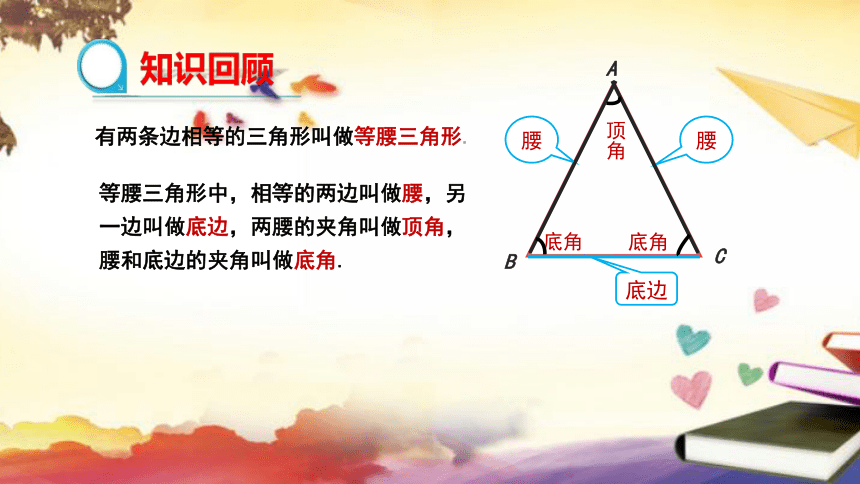
知识回顾
A
C
B
腰
腰
底边
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
顶角
底角
底角
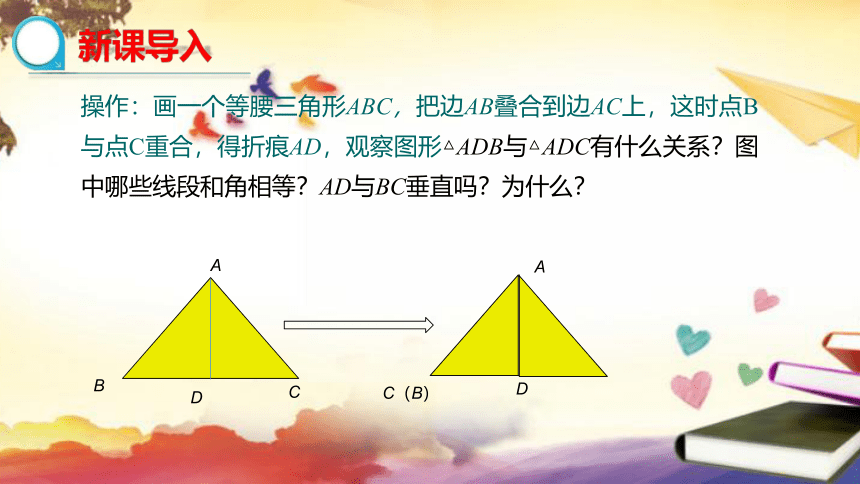
新课导入
操作:画一个等腰三角形ABC,把边AB叠合到边AC上,这时点B与点C重合,得折痕AD,观察图形△ADB与△ADC有什么关系?图中哪些线段和角相等?AD与BC垂直吗?为什么?
A
B
C
A
C(B)
D
D
思考: (1)△ABC 是轴对称图形吗?它的对称轴是什么?
(2)△ADB 与△ADC 有什么关系?图中有哪些线段或角相等?AD与BC垂直吗?为什么?
A
C
D
B
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
知识讲解
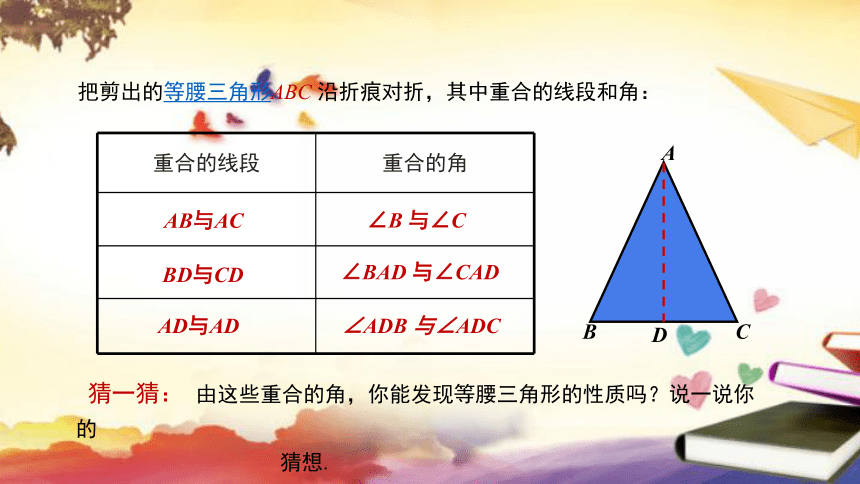
把剪出的等腰三角形ABC 沿折痕对折,其中重合的线段和角:
重合的线段 重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜: 由这些重合的角,你能发现等腰三角形的性质吗?说一说你的
猜想.
发现:
(1)等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴;
(2)等腰三角形的两个底角相等,即∠B=∠C;
(3)即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线.
A
B
C
D
A
B
C
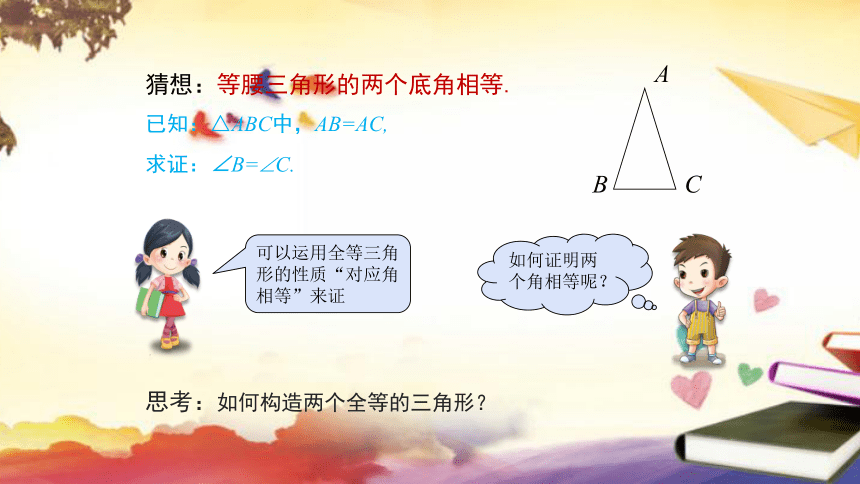
已知:△ABC中,AB=AC,
求证:∠B= C.
思考:如何构造两个全等的三角形?
猜想:等腰三角形的两个底角相等.
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
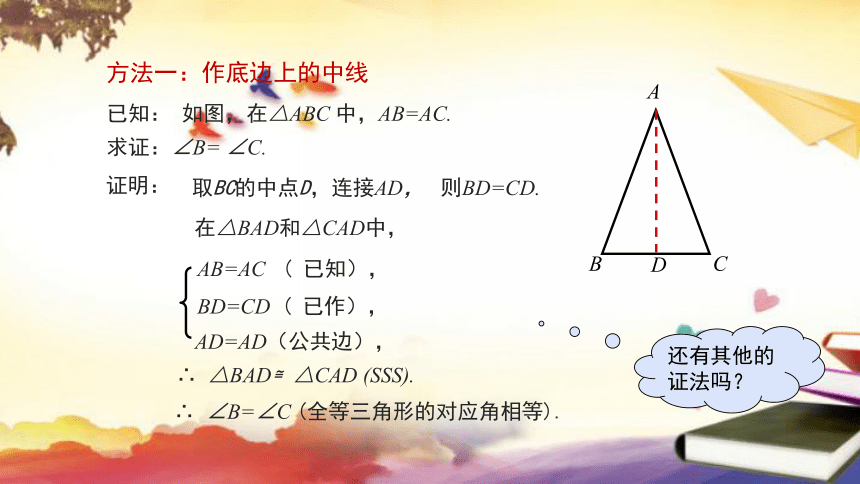
已知: 如图,在△ABC 中,AB=AC.
求证:∠B= ∠C.
A
B
C
D
证明:
取BC的中点D,连接AD, 则BD=CD.
AB=AC ( 已知),
BD=CD ( 已作),
AD=AD(公共边),
∴ △BAD≌△CAD (SSS).
∴ ∠B=∠C (全等三角形的对应角相等).
在△BAD和△CAD中,
方法一:作底边上的中线
还有其他的证法吗?
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中,
A
B
C
D
归纳:
定理1:等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
想一想:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的
角平分线、底边BC上的高线 .
A
B
C
D
A
C
B
D
1
2
(1)∵AB=AC, ∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
(2)∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
(3)∵AB=AC, AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一).
如图,在△ABC中,
归纳:
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角的平分线、底边上的中线和底边上的高“三线合一”.
例1已知:如图,在△ABC中,AB=AC,∠BAC=120°,点D,E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
解∵AB=AC,(已知)
∴∠B=∠C.(等边对等角)
∴∠B=∠C= ×(180°-120°)=30°
又∵BD=AD,(已知)
∴∠BAD=∠B=30°(等边对等角)
同理,∠CAE=∠C=30°,
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°
A
B
C
D
E
思考?
本例中去掉AB=AC这个条件,能否求出∠DAE的度数?
2、等边三角形的性质
A
B
C
A
B
C
问题1 等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AC=BC
∠A=∠B
∠A=∠B=∠C
内角和
为180°
=60°
探究
结论:等边三角形的三个内角都相等,并且每一 个角都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
A
B
C
问题2 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
总结
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
例2 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE
=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
例3 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
图②
图①
证明:
(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图②
图①
G
总结:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
随堂训练
1、等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
A
2、如图,在△ABC中,AB=AC,过点A作AD∥BC,
若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
3、(1)等腰三角形一个底角为75°,它的另外两个角为 ;
(2)等腰三角形一个角为36°,它的另外两个角为 ;
(3)等腰三角形一个角为120°,它的另外两个角为 .
75°, 30°
72°,72°或36°,108°
30°,30°
4、在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角
为50°,则底角的大小为_________.
A
B
C
A
B
C
70°或20°
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
5、如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解: ∵AB=AD=DC,
∴ ∠B= ∠ADB,∠C= ∠DAC.
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x,
在△ABC中, 根据三角形内角和定理,
得2x+x+26°+ x=180°,
解得x=38.5°.
∴ ∠C= x=38.5°, ∠B=2x=77°.
6、如图,已知△ABC为等腰三角形,BD、CE为底角的平分线,且∠DBC=∠F,求证:EC∥DF.
∴∠DBC=∠ECB.
∵∠DBC=∠F,∴∠ECB=∠F,
∴EC∥DF.
证明:∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
又∵BD、CE为底角的平分线,
∴
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
15.3 等腰三角形
第1课时 等腰三角形的性质
第15章 轴对称图形与等腰三角形
理解并掌握等腰三角形的性质及其推论;(重点)
能运用等腰三角形的性质及其推论解决基本的几何问题.(难点)
学习目标
1
2
3
经历操作、思考、探究证明等腰三角形的有关定理的过程,进一步掌握证明的基本步骤和书写格式;
知识回顾
A
C
B
腰
腰
底边
有两条边相等的三角形叫做等腰三角形.
等腰三角形中,相等的两边叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
顶角
底角
底角
新课导入
操作:画一个等腰三角形ABC,把边AB叠合到边AC上,这时点B与点C重合,得折痕AD,观察图形△ADB与△ADC有什么关系?图中哪些线段和角相等?AD与BC垂直吗?为什么?
A
B
C
A
C(B)
D
D
思考: (1)△ABC 是轴对称图形吗?它的对称轴是什么?
(2)△ADB 与△ADC 有什么关系?图中有哪些线段或角相等?AD与BC垂直吗?为什么?
A
C
D
B
折痕所在的直线是它的对称轴.
等腰三角形是轴对称图形.
知识讲解
把剪出的等腰三角形ABC 沿折痕对折,其中重合的线段和角:
重合的线段 重合的角
A
C
B
D
AB与AC
BD与CD
AD与AD
∠B 与∠C
∠BAD 与∠CAD
∠ADB 与∠ADC
猜一猜: 由这些重合的角,你能发现等腰三角形的性质吗?说一说你的
猜想.
发现:
(1)等腰三角形是轴对称图形,底边上的中线所在的直线是它的对称轴;
(2)等腰三角形的两个底角相等,即∠B=∠C;
(3)即AD是等腰△ABC底边BC上的中线、顶角∠BAC的角平分线、底边BC上的高线.
A
B
C
D
A
B
C
已知:△ABC中,AB=AC,
求证:∠B= C.
思考:如何构造两个全等的三角形?
猜想:等腰三角形的两个底角相等.
如何证明两个角相等呢?
可以运用全等三角形的性质“对应角相等”来证
已知: 如图,在△ABC 中,AB=AC.
求证:∠B= ∠C.
A
B
C
D
证明:
取BC的中点D,连接AD, 则BD=CD.
AB=AC ( 已知),
BD=CD ( 已作),
AD=AD(公共边),
∴ △BAD≌△CAD (SSS).
∴ ∠B=∠C (全等三角形的对应角相等).
在△BAD和△CAD中,
方法一:作底边上的中线
还有其他的证法吗?
已知:如图,在△ABC中,AB=AC.
求证:∠B=∠C.
证明:
作顶角的平分线AD,
则∠BAD=∠CAD.
AB=AC ( 已知 ),
∠BAD=∠CAD ( 已作 ),
AD=AD (公共边),
∴ △BAD ≌ △CAD (SAS).
∴ ∠B= ∠C (全等三角形的对应角相等).
方法二:作顶角的平分线
在△BAD和△CAD中,
A
B
C
D
归纳:
定理1:等腰三角形的两个底角相等(等边对等角).
A
C
B
如图,在△ABC中,
∵AB=AC(已知),
∴∠B=∠C(等边对等角).
想一想:由△BAD≌ △CAD,除了可以得到∠B= ∠C之外,你还可以得到那些相等的线段和相等的角?和你的同伴交流一下,看看你有什么新的发现?
解:∵△BAD≌ △CAD,由全等三角形的性质易得BD=CD,∠ADB=∠ADC,∠BAD=∠CAD.
又∵ ∠ADB+∠ADC=180°,
∴ ∠ADB=∠ADC= 90° ,
即AD是等腰△ABC底边BC上的中线、顶角∠BAC的
角平分线、底边BC上的高线 .
A
B
C
D
A
C
B
D
1
2
(1)∵AB=AC, ∠1=∠2(已知),
∴BD=CD,AD⊥BC(等腰三角形三线合一).
(2)∵AB=AC, BD=CD (已知),
∴∠1=∠2,AD⊥BC(等腰三角形三线合一).
(3)∵AB=AC, AD⊥BC(已知),
∴BD=CD, ∠1=∠2(等腰三角形三线合一).
如图,在△ABC中,
归纳:
定理2:等腰三角形顶角的平分线垂直平分底边.
等腰三角形顶角的平分线、底边上的中线和底边上的高“三线合一”.
例1已知:如图,在△ABC中,AB=AC,∠BAC=120°,点D,E是底边上两点,且BD=AD,CE=AE.求∠DAE的度数.
解∵AB=AC,(已知)
∴∠B=∠C.(等边对等角)
∴∠B=∠C= ×(180°-120°)=30°
又∵BD=AD,(已知)
∴∠BAD=∠B=30°(等边对等角)
同理,∠CAE=∠C=30°,
∴∠DAE=∠BAC-∠BAD-∠CAE
=120°-30°-30°=60°
A
B
C
D
E
思考?
本例中去掉AB=AC这个条件,能否求出∠DAE的度数?
2、等边三角形的性质
A
B
C
A
B
C
问题1 等边三角形的三个内角之间有什么关系?
等腰三角形
AB=AC
∠B=∠C
等边三角形
AB=AC=BC
AC=BC
∠A=∠B
∠A=∠B=∠C
内角和
为180°
=60°
探究
结论:等边三角形的三个内角都相等,并且每一 个角都等于60°.
已知:AB=AC=BC ,
求证:∠A= ∠ B=∠C= 60°.
证明: ∵AB=AC.
∴∠B=∠C .(等边对等角)
同理 ∠A=∠C .
∴∠A=∠B=∠C.
∵ ∠A+∠B+∠C=180°,
∴ ∠A= ∠B= ∠C=60 °.
A
B
C
A
B
C
问题2 等边三角形有“三线合一”的性质吗 等边三角形有几条对称轴?
结论:等边三角形每条边上的中线,高和所对角的平分线都“三线合一”.
顶角的平分线、底边的高
底边的中线
三线合一
一条对称轴
三条对称轴
总结
图形 等腰三角形
性 质
每一边上的中线、高和这一边所对的角的平分线互相重合
三个角都相等,
对称轴(3条)
等边三角形
对称轴(1条)
两个底角相等
底边上的中线、高和顶角的平分线互相重合
且都是60
两条边相等
三条边都相等
例2 如图,△ABC是等边三角形,E是AC上一点,D是BC延长线上一点,连接BE,DE,若∠ABE=40°,BE=DE,求∠CED的度数.
解:∵△ABC是等边三角形,
∴∠ABC=∠ACB=60°.
∵∠ABE=40°,
∴∠EBC=∠ABC-∠ABE
=60°-40°=20°.
∵BE=DE,
∴∠D=∠EBC=20°,
∴∠CED=∠ACB-∠D=40°.
例3 已知点D、E在△ABC的边BC上,AB=AC.
(1)如图①,若AD=AE,求证:BD=CE;
(2)如图②,若BD=CE,F为DE的中点,求证:AF⊥BC.
图②
图①
证明:
(1)如图①,过A作AG⊥BC于G.
∵AB=AC,AD=AE,
∴BG=CG,DG=EG,
∴BG-DG=CG-EG,
∴BD=CE;
(2)∵BD=CE,F为DE的中点,
∴BD+DF=CE+EF,
∴BF=CF.
∵AB=AC,∴AF⊥BC.
图②
图①
G
总结:在等腰三角形有关计算或证明中,有时需要添加辅助线,其顶角平分线、底边上的高、底边上的中线是常见的辅助线.
随堂训练
1、等腰三角形的一个内角是50°,则这个三角形的底角的大小是( )
A.65°或50° B.80°或40°
C.65°或80° D.50°或80°
A
2、如图,在△ABC中,AB=AC,过点A作AD∥BC,
若∠1=70°,则∠BAC的大小为( )
A.40° B.30° C.70° D.50°
A
3、(1)等腰三角形一个底角为75°,它的另外两个角为 ;
(2)等腰三角形一个角为36°,它的另外两个角为 ;
(3)等腰三角形一个角为120°,它的另外两个角为 .
75°, 30°
72°,72°或36°,108°
30°,30°
4、在△ABC中, AB=AC,AB的垂直平分线与AC所在的直线相交得的锐角
为50°,则底角的大小为_________.
A
B
C
A
B
C
70°或20°
注意:当题目未给定三角形的形状时,一般需分锐角三角形和钝角三角形两种情况进行讨论.
5、如图,在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
解: ∵AB=AD=DC,
∴ ∠B= ∠ADB,∠C= ∠DAC.
设 ∠C=x,则 ∠DAC=x,
∠B= ∠ADB= ∠C+ ∠DAC=2x,
在△ABC中, 根据三角形内角和定理,
得2x+x+26°+ x=180°,
解得x=38.5°.
∴ ∠C= x=38.5°, ∠B=2x=77°.
6、如图,已知△ABC为等腰三角形,BD、CE为底角的平分线,且∠DBC=∠F,求证:EC∥DF.
∴∠DBC=∠ECB.
∵∠DBC=∠F,∴∠ECB=∠F,
∴EC∥DF.
证明:∵△ABC为等腰三角形,AB=AC,
∴∠ABC=∠ACB.
又∵BD、CE为底角的平分线,
∴
课堂小结
等腰三角形的性质
等边对等角
三线合一
注意是指同一个三角形中
注意是指顶角的平分线,底边上的高和中线才有这一性质.而腰上高和中线与底角的平分线不具有这一性质.
